Prasanna

You can Download Samacheer Kalvi 9th Social Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Social Science Civics Solutions Chapter 2 Election, Political Parties and Pressure Groups

Election, Political Parties and Pressure Groups Textual Exercise

I. Choose the correct answer.

Question 1.
India has adapted the electoral system followed in the
(a) USA
(b) United Kingdom
(c) Canada
(d) Russia
Answer:
(b) United Kingdom

Question 2.
The Election Commission of India is a/an
(a) Independent body
(b) Statutory body
(c) Private body
(d) Public corporation
Answer:
(a) Independent body

Question 3.
Which Article of the Constitution provides for an Election Commission?
(a) Article 280
(b) Article 315
(c) Article 324
(d) Article 325
Answer:
(c) Article 324

Question 4.
Which part of the constitution of India says about the election commission?
(a) Part III
(b) Part XV
(c) Part XX
(d) Part XXII
Answer:
(b) Part XV

Question 5.
Who accords recognition to various political parties as national or regional parties?
(a) The President
(b) The Election Commission
(c) The Parliament
(d) The President in consultation with the Election Commission
Answer:
(b) The Election Commission

Question 6.
Assertion (A): Indian Constitution provides for an independent Election Commission
Reason (R): To ensure free and fair elections in the country.
(a) Both (A) and (R) are true and (R) explains (A)
(b) Both (A) and (R) are true and (R) does not explain (A)
(c) (A) is correct and (R) is false
(d) (A) is false and (R) is true
Answer:
(a) Both (A) and (R) are true and (R) explains (A)

Question 7.
NOT A was introduced in the year ………..
(a) 2012
(b) 2013
(c) 2014
(d) 2015
Answer:
(c) 2014

Question 8.
The term pressure groups originated in …….
(a) USA
(b) the UK
(c) USSR
(d) India
Answer:
(a) USA

Question 9.
Assertion (A): A large number of pressure groups exist in India.
Reason (R): Pressure Groups are not developed in India to the same extent as in the USA.
(a) Both (A) and (R) are true and (R) explains (A)
(b) Both (A) and (R) are true and (R) does not explain (A)
(c) (A) is correct and (R) is false
(d) (A) is false and (R) is true
Answer:
(a) Both (A) and (R) are true and (R) explains (A)

II. Fill in the blanks.

1. The Election Commission of India is a body of ……… members.
2. National Voters day has been celebrated on ………
3. In India ……… party system is followed.
4. In 2017, there were ……. recognised national parties.
5. Narmada Bachao Andolan is a …………

Answers:

1. 3
2. 25^th January
3. Multi
4. Seven
5. Pressure group

III. Match the following.

Answers:
1. (d)
2. (c)
3. (b)
4. (a)

IV. Give short answers.

Question 1.
Explain the electoral system in India.
Answer:

1. The Electoral system in India is borrowed from the one operating systems in Great Britain.
2. The constitution (Article 324) provides for an independent Election Commission in order to ensure free and fair elections in the country.
3. Parliament may make provisions with respect to all matters relating to the election in the Parliament and the State Legislative.
4. The State Legislative can also make provisions with respect to all matters relating to elections to the State Legislative. But they can only supplement the parliamentary law.

Question 2.
Give the meaning of a political party.
Answer:
A political party is an organisation formed by a group of people with a certain ideology and agenda to contest elections and hold power in the government.

A political party has three components: a leader, active members and followers.

Question 3.
Distinguish between the two-party system and the multi-party system.
Answer:

Two-party system	Multi-party system
The two-party system in which only two major parties exist, for example, USA, UK.	The multi-party system in which there are more than two political parties, for example, India, Srilanka, France and Italy.

Question 4.
What is a pressure group?
Answer:

1. The term ‘Pressure group’ originated in the USA.
2.  A pressure group is a group of people who are organised activities for promoting and defending their common interest.
3. It is so-called, as it attempts to bring a change in the public policy by exerting pressure on the government.

V. Answer in detail.

Question 1.
Discuss the merits and demerits of direct elections?
Answer:
Merits of Direct elections:

1. As the voters elect their representatives directly, direct elections are considered to be a more democratic method of election.
2. It educates people regarding government activities and helps in choosing the appropriate candidates. Also, it encourages people to play an active role in politics.
3. It empowers people and makes the rulers accountable for their actions.

Demerits of Direct elections:

1. Direct elections are very expensive.
2. Illiterate voters sometimes get misguided by false propaganda and sometimes campaigning based on caste, religion and various other sectarian considerations pose serious challenges.
3. Since conducting direct elections is a massive exercise, ensuring free and fair elections at every polling station is a major challenge to the Election Commission.
4. There are instances of some political candidates influencing the voters through payments in the form of cash, goods, or services.
5. Election campaigns sometimes result in violence, tension, law and order problems and affect the day-to-day life of people.

Question 2.
What are the functions of political parties?
Answer:

1. Parties contest elections. In most democracies, elections are fought mainly among the candidates put up by political parties.
2. Parties put forward their policies and programmes before the electorate to consider and choose.
3. Parties play a decisive role in making laws for a country. Formally, laws are debated and passed in the legislature.
4. Parties form and run the governments.
5. Those parties that lose in the elections play the role of the Opposition to the party or a group of coalition parties in power, by voicing different views and criticising the government for its failures or wrong policies.
6. Parties shape public opinion. They raise and highlight issues of importance.
7. Parties function as a useful link between people and the government machinery.

Question 3.
What are the functions of Pressure groups in India?
Answer:
Pressure groups carry out a range of functions including Representation, Political Participation, Education, Policy formulation, and Policy implementation.

(a) Representation
Pressure groups provide an alternative to the formal representative process or the functional representation by providing mouthpieces for groups and interests that are not adequately represented through, the electoral process or by political parties.

(b) Political Participation

1. Pressure groups can be called the informal face of politics.
2. They exert influence precisely by mobilizing popular support through activities such as petitions, marches, demonstrations, and other forms of political protest.
3. Such forms of political participation have been particularly attractive to young people.

(c) Education
Many pressure groups devote significant resources by carrying out research, maintaining websites, commenting on government policy, and using high-profile academics, scientists and even celebrities to get their views across, with an emphasis to cultivate expert authority.

(d) Policy Formulation:

1. Though the pressure groups themselves are not policy-makers, yet this does not prevent many of them from participating in the policy-making process.
2. Many Pressure groups are vital sources of information and render advice to the government and therefore they are regularly consulted in the process of policy formulation

(e) Policy Implementation

1. Occasionally pressure groups implement policy or play a role in it.
2. A good example is a blue cross which helps the government in protecting animal welfare

VI. Project and Activity

Question 1.
Compare the policies, programmes, and achievements of a national party and a state party.
Answer:

1. Refer to the National policies, programmes, and achievements from the Internet and library books.
2. The students are instructed to compare policy programmes and achievements.
3. This is a group activity.

VII. HOTS

Question 1.
“Elections are considered essential for any representative democracy”. Why?
Answer:
“A democracy requires a mechanism by which people can choose their representatives at regular intervals and change them if they wish to do so. Therefore, elections are considered essential for any representative democracy. In an election, the voters make many choices.

1. This helps the public in choosing the development course which they want and want to adopt.
2. This directly provides the public the opportunity to select their representatives and these representatives decision can be legitimacy.
3. This also ensures transparency, as well as accountability as the public representatives, are chosen directly.

Question 2.
What is the principle of the universal adult franchise? What is its importance?
Answer:
Principle: Universal Adult Franchise means that the right to vote should be given to all adult citizens without the discrimination of caste, class, colour, religion (or) gender. It is based on equality, which is a basic principle of democracy.

Importance: Under this system, a government is elected that is accountable to the people it governs. Because every vote counts, issues in society receive their appropriate weight in terms of importance and urgency.

Question 3.
Discuss the merits and demerits of democracy.
Answer:

	Merits		Demerits
1.	Safeguards the interests of the people.	1.	More emphasis on quantity than on quality.
2.	Based on the principle of equality.	2.	Rule of the incompetent.
3.	Stability and responsibility in administration.	3.	Based on unnatural equality.
4.	Political education to the people.	4.	Voters do not take interest in elections.
5.	Little chance of revolution.	5.	Lowers the moral standard.
6.	Stable government.	6.	Democracy is a government of the rich.
7.	Helps in making people good citizens.	7.	Misuse of public funds and time.
8.	Based on public opinion.	8.	No stable government.
		9.	The dictatorship of majority.
		10.	Bad influence of political parties.

Question 4.
Discuss the multi-party system.
Answer:

1. A multi-party system is a system where multiple political parties that have ideas participate in the national elections.
2. A lot of countries that use this system have a coalition government, meaning many parties are in control, and they all work together to make laws.
3. Countries with a multi-party political system tend to have greater voter participation.
4. No democracy can survive without a multi-party system.

VIII. Life Skill

Question 1.
Conduct a mock poll in your classroom.
Answer:

1. Help the students to understand the process of electing officials and the power of vote by holding a mock election.
2. These are great activities to enjoy during the presidential election.
3. Students explain the steps taken from party formation to National election.
4. The students will act out the campaigning and voting process by stimulating a real election in their own classroom.

Steps set for a mock-poll in the classroom:

1. Setting up the political parties.
2. Preparing a manifesto.
3. Running a campaign.
4. Holding the classroom election.

Election, Political Parties and Pressure Groups Additional Questions

I. Choose the correct answer.

Question 1.
India is the democracy in the world.
(a) largest
(b) smallest
(c) strongest
(d) None of the above
Answer:
(a) largest

Question 2.
Kudavolai was the system of voting followed during the ……. period in Tamil Nadu.
(a) Chera
(b) Chola
(c) Pandya
(d) Pallava
Answer:
(b) Chola

Question 3.
Which country has single-party system?
(a) USA
(b) UK
(c) Cuba
(d) France
Answer:
(c) Cuba

Question 4.
Assertion (A): Parties shape public opinion.
Reason (R): They raise and highlight issues of importance.
(a) Both (A) and (R) are true and (R) explains (A)
(b) Both (A) and (R) are true and (R) does not explain (A).
(c) (A) is correct and (R) is false
(d) (A) is false and (R) is true
Answer:
(a) Both (A) and (R) are true and (R) explains (A)

Question 5.
India is the ………… th country in the world to introduce NOTA.
(a) 10
(b) 12
(c) 14
(d) 16
Answer:
(c) 14

Question 6.
The ……. is elected by members of the Lok Sabha.
(a) Prime Minister
(b) President
(c) Governor
(d) Cabinet Minister
Answer:
(a) Prime Minister

II. Fill in the blanks.

1. ……. in elections are the best way to make your ‘voice’ heard.
2. Indirect elections are less ……..
3. ……… parties are an essential part of Democracy.
4. …… treats all the parties equally.
5. The pressure groups are also called ……. groups.
6. A political party has three components: a ………. and the ……….

Answers:

1. Voting
2. Expensive
3. Political
4. Election Commission
5. Interest
6. a leader, acting members, followers

III. Match the following.

Answers:
1. (d)
2. (a)
3. (b)
4. (c)

IV. Give short answers.

Question 1.
What do you know about Voters Verified Paper Audit Trail?
Answer:

1. Voters Verified Paper Audit Trail (WPAT) is the way forward to enhance credibility and transparency of the election process.
2. This system was first introduced in the 2014 General election.

Question 2.
Mention the merits and demerits of Indirect elections.
Answer:
Merits:

1. Indirect elections are less expensive.
2. It is more suited to elections in large countries.

Demerits:

1. If the number of voters is very small, there exists the possibility of corruption, bribery, horse-trading, and other unfair activities.
2. It is less democratic because people do not have a direct opportunity to elect, but they instead do it through their representatives. So, this may not reflect the true will of the people.

Question 3.
Write a short note on “State Parties”.
Answer:
Other than the seven national parties, most of the major parties of the country are classified by the Election Commission as ‘state parties’. These are commonly referred to as regional parties. A party is recognised as a state party by the Election Commission of India based on a certain percentage of votes secured or a certain number of seats won in the Assembly or Lok Sabha elections.

Question 4.
Classify pressure groups in India.
Answer:
The pressure groups in India can be broadly classified into the following categories:

1. Business groups
2. Trade unions
3. Agrarian groups
4. Professional associations
5. Student organisations
6. Religious organisations
7. Tribal organisations
8. Linguistic groups
9. Ideology-based groups
10. Environmental protection groups.

V. Answer in detail.

Question 1.
Give an account of Mobilisation and Democratic Participation.
Answer:
Mobilising people towards socially productive activities that lead to the overall betterment of people’s lives is essential. Sometimes earthquakes, tsunamis, floods, and other such natural disasters on a massive scale occur and people’s immediate mobilisation for evacuation and emergency relief becomes most essential.

Democratic Participation: Democracy can-succeed only when smaller local groups and, in fact, every citizen can take action that supports the tax and revenue collection systems, observance of national norms in environmental protection, cleanliness, health and hygiene, sanitary drives, and immunisation programmes like pulse polio.

However, we must keep in mind that there is no better form of government than a Democratic government. To create a better society and nation, the people of India along with the union and state governments should come together to fight against the miseries of human life.

You can Download Samacheer Kalvi 9th Social Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Social Science History Solutions Chapter 2 Ancient Civilisations

Ancient Civilisations Textual Exercise

I. Choose the correct answer.

Question 1.
The earliest signs to denote words through pictures ……………
(a) Logographic
(b) Pictographic
(c) Ideographic
(d) Stratigraphic
Answer:
(b) Pictographic

Question 2.
The preservation process of dead body in ancient Egypt ……………
(a) Sarcophagus
(b) Hyksos
(c) Mummification
(d) Polytheism
Answer:
(c) Mummification

Question 3.
The Sumerian system of writing : ……………
(a) Pictographic
(b) Hieroglyphic
(c) Sonogram
(d) Cuneiform
Answer:
(b) Hieroglyphic

Question 4.
The Harappans did not have the knowledge of ……………
(a) Gold and Elephant
(b) Horse and Iron
(c) Sheep and Silver
(d) Ox and Platinum
Answer:
(d) Ox and Platinum

Question 5.
The Bronze image suggestive of the use of lost-wax process known to the Indus people.
(a) Jar
(b) Priest king
(c) Dancing girl
(d) Bird
Answer:
(c) Dancing girl

Question 6.
(i) The oldest civilisation in Mesopotamia belonged to the Akkadians.
(ii) The Chinese developed the Hieroglyphic system.
(iii) The Euphrates and Tigris drain into the Mannar Gulf.
(iv) Hammurabi, the king of Babylon was a great law maker. .
(a) (i) is correct
(b) (i) and (ii) are correct
(c) (iii) is correct
(d) (iv) is correct
Answer:
(d) (iv) is correct

Question 7.
(i) Yangtze River is known as Sorrow of China.
(ii) Wu-Ti constructed the Great Wall of China.
(iii) Chinese invented gun powder.
(iv) According to traditions Mfencius was the founder of Taoism.
(a) (i) is correct
(b) (ii) is correct
(c) (iii) is correct
(d) (iii) and (iv) are correct
Answer:
(c) (iii) is correct

Question 8.
What is the correct chronological order of four civilisations of Mesopotamia?
(a) Sumerians – Assyrians – Akkadians – Babylonians
(b) Babylonians – Sumerians – Assyrians – Akkadians
(c) Sumerians – Akkadians – Babylonians – Assyrians
(d) Babylonians – Assyrians – Akkadians – Sumerians
Answer:
(c) Sumerians – Akkadians – Babylonians – Assyrians

Question 9.
Assertion (A): Assyrians of Mesopotamian civilisation were contemporaries of Indus civilisation.
Reason (R): The Documents of an Assyrian ruler refer to the ships from Meluha.
(a) A and R are correct and A explains R
(b) A and R are correct but A doesn’t explain R
(c) A is incorrect but R is correct
(d) Both A and R are incorrect
Answer:
(d) Both A and R are incorrect

II. Fill in the blanks.

1. ……………. is a massive lime stone image of a lion with a human head.
2. The early form of writing of the Egyptians is known as ……………
3. ……………. specifies the Laws related to various crimes in ancient Babylonia.
4. …………… was the master archive keeper of Chou state, according to traditions.
5. The …………… figurines and paintings on the pottery from the sites suggest the artistic skills of the Harappans.
Answers:
1. The Great Sphinx of Ghiza
2. Hieroglyphic
3. Hammurabi code
4. Lao Tze
5. terracotta

III. Find out the correct statement.

Question 1.
(a) The Great Bath at Harappa is well-built with several adjacent rooms.
(b) The cuneiform inscriptions relate to the epic of Gilgamesh.
(c) The terracotta figurines and dancing girl made of copper suggest the artistic skills of Egyptians.
(d) The Mesopotamians devised a solar calendar system.
Answer:
(a) correct
(b) correct
(c) incorrect
(d) incorrect

Question 2.
(a) Amon was considered the king of god in ancient Egypt.
(b) The fortified Harappan city had the temples.
(c) The great sphinx is a pyramid-shaped monument found in ancient Mesopotamia.
(d) The invention of the potter’s wheel is Credited to the Egyptians.
Answer:
(a) correct
(b) incorrect
(c) incorrect
(d) incorrect

IV. Match the following.

Answer:
1. (e)
2. (a)
3. (d)
4. (b)
5. (c)

V. Answer the following briefly.

Question 1.
The Egyptians excelled in art and architecture. Illustrate.
Answer:

1. Numerous sculptures, paintings, and carvings attest to the artistic skills of Egyptians.
2. The pyramids are massive monuments built as tombs of mourning to the Pharaohs.
3. The great pyramids near Cairo are known as the Giza Pyramids.
4. Pyramids are considered to be one of the wonders of the world.
5. These monuments display the-engineering, architectural, and human resource management skills of the Egyptians.
6. The Great Sphinx of Giza is a massive limestone image of a lion with a human head.
7. It is one of the largest sculptures in the world.

Question 2.
State the salient features of the Ziggurats.
Answer:

1. Ziggurats were pyramid-shaped monuments found in the ancient Mesopotamia (Modem Iraq).
2. One of the most famous Ziggurats of the time is the one in the city of Ur.
3. The Ziggurats were at the city centre on a platform and appeared like steep pyramids with staircases leading to the top.

Question 3.
Hammurabi Code is an important legal document. Explain.
Answer:

1. Hammurabi code is an important legal document that specifies the laws related to various crimes.
2. It has 282 provisions specifying cases related to family rights, trade, slavery, taxes, and wages.
3. It is carved on a stone, which portrays Hammurabi as receiving the code from the Sun God Shamash.
4. The ‘eye for an eye’ and ‘tooth for tooth’ form of justice is used in the Hammurabi Code.

Question 4.
Write a note on the Great Wall of China.
Answer:

• The Great Wall of China, one of the wonders of the world, was a massive effort undertaken for the protection of China from the Mongols.
• In 220 BCE, under Qin Shi Huang, earlier fortifications were connected by walls as a form of defence against invasions.
• It was built from third century BCE until 17th century CE.
• It ran for over 20,000 kilometres covering the hills and plains, from the border of Korea in the east to the Ordos Desert in the west.

VI. Answer all the questions given under each caption.

1. Early Civilizations:
Question 1.
What is meant by civilization?
Answer:
(a) Civilisation is seen as an advanced, organised way of life.
(b) It instilled a way of life that could be considered as an adaptation to particular environmental and cultural contents.

Question 2.
Name the important early Civilizations.
Answer:
The Egyptian, Mesopotamian, the Chinese and the Indus were the important Civilisations.

Question 3.
What supported the livelihood of a large number of people?
Answer:
The surplus food production by the farmers in the fertile regions supported the livelihood of. a large number of people.

Question 4.
What happened when civilization began to take shape?
Answer:
As civilizations began to take shape, huge buildings were built, the art of writing developed and science and technology contributed to the betterment of society.

2. Features of Egyptian Civilization:
Question 1.
Who built the pyramids and why?
Answer:
The pyramids are massive monuments built by Egyptians as tombs of mourning to the Pharaohs. The Great Pyramids near Cairo are known as the Gizza Pyramids.

Question 2.
What is the process of mummification?
Answer:

• The Egyptians had the tradition of preserving the dead bodies using Natron salt;, a combination of sodium carbonate and sodium bicarbonate.
• The preservation process is called mummification.
• After 40 days when the salt absorbed all the moisture, the body was filled with sawdust and wrapped in strips of linen clothes and covered with fabric. The body was stored in a stone coffin called a sarcophagus.

Question 3.
What is the belief system of ancient Egyptians?
Answer:
(a) The Egyptians believed in life after death.
(b) Egyptian practiced polytheism. They worshipped many gods.

Question 4.
What is the importance of great sphinx?
Answer:
The Great Sphinx of Giza is a massive limestone image of a lion with a human head.
It is dated to the time of Pharaoh Kaffe. It is one of the largest sculptures of the world and measures seventy three metres in length and twenty metres in height.

VII. Answer the following in detail.

Question 1.
Define the terms Hieroglyphics and Cuneiform with their main features.
Answer:
Hieroglyphics: Egyptians are well known for their writing system. Their form of writing is known as hieroglyphics. Hieroglyphic was used in the inscriptions on seals and other objects. The heretic, an another form of writing, was used for common purposes. This form of writing used a pictogram-based system. It was developed around 3000 BCE and many texts and books were written using this script.

The Egyptian writing system was deciphered by the French scholar, Francois Champollion (1822 CE). He used the Rosetta stone, a trilingual inscription, for deciphering the script. This inscription, which was written in Hieroglyphic, Demotic and Greek,- was taken to France by Napoleon and from there it was taken to England. Now, this inscription is on display in the British Museum London.

Cuneiform: Cuneiform is the Sumerian writing system. The shape of the letter is in the form of wedge and hence it is called cuneiform. Evolving around 3000 BCE, it is one of the earliest scripts of the world. The epic of Gilgamesh was written in this script. They used this script for commercial transactions and writing letters and stories. The clay tablets contain loads of information on the Sumerian civilization.

Question 2.
To what extent is the Chinese influence reflected in the fields of philosophy and literature.
Answer:
(i) Chinese poets and philosophers such as Lao Tze, Confucius, Mencius, Mo Ti (Mot Zu) and Tao Chien (365-427 CE) contributed to the development of Chinese civilization. Sun-Tzu, a military strategist, wrote the work called Art of War.

(ii) The Spring and Autumn Annals is the official chronicle of the state at the time. The Yellow Emperor’s Canon of Medicine is considered China’s earliest written book on medicine. It was codified during the time of Han Dynasty.

(iii) Lao Tze (c. 604-521 BCE) was the master archive keeper of Chou state. He was the founder of Taoism. He argued that desire is the root cause of all evils.

(iv) Confucius (551-497 BCE) was famous among the Chinese philosophers. He was a political reformer. His name means Kung the master.

(v) He insisted on cultivation of one’s own personal life. He said, “If personal life is cultivated, family life is regulated; and once family life is regulated, national life is regulated.

(vi) Mencius (372-289 BCE) was another well-known Chinese philosopher. He traveled throughout China and offered his counsel to the rulers.

Student Activities

Question 1.
Mark the areas of Bronze Age civilization on the world map.
Answer:
The Bronze Age period: 3300 – 1200 B.C.
The location: China
(i) The Congshan people of China lived from around 300 B.C. to 2400 B.C. in China
(ii) Around 2300 B.C. in Europe.
The teacher can help the students to locate the place on the world map.

Question 2.
Prepare a chart on the pyramids and the mummies.
Answer:
Prepare a chart on the Pyramids and the Mummies with guidelines from the Textbook and the Internet. Students can be divided into groups & prepare the charts on the Pyramids and Mummies.

Question 3.
Collect the pictures of the seals and the pottery of the Indus people.
Answer:
Download the pictures & collect them.
Assignment with teacher’s guidance
(i) Prepare a hand out comparing the ancient world civilizations.
Reference: Textbook & Internet
(ii) Prepare a scrapbook collecting pictures on Indus civilization from website.
Students can collect pictures on Indus Civilization and paste them into their scrapbook.

Ancient Civilisations Additional Questions

I. Choose the correct answer.

Question 1.
……………… times were mostly egalitarian in nature.
(a) Mesolithic
(b) Neolithic
(c) Palaeolithic
(d) Iron Age
Answer:
(a) Mesolithic

Question 2.
……………… became intimately connected with the Sangam Age Tamitagam by the Sea route.
(a) Romans
(b) Persians
(c) Egyptians
(d) Greeks
Answer:
(c) Egyptians

Question 3.
…………… were the contemporaries of the people of Indus and Egyptian civilisation.
(a) The Egyptians
(b) The Sumerians
(c) The Romans
(d) The Indus people
Answer:
(b) The Sumerians

Question 4.
……………. did not give much attention to life after death.
(a) The Sumerians
(b) The Babylonians
(c) The Egyptians
(d) The Chinese
Answer:
(a) The Sumerians

Question 5.
The yellow river is known as the sorrow of …………
(a) Egypt
(b) Rome
(c) China
(d) Iraq
Answer:
(c) China

Question 6.
(i) The Egyptian king was known as the Pharaoh.
(ii) The preserved dead body is called the mummy.
(iii) The Egyptians have no belief in life after death.
(iv) Papyrus was used for making paper.
(a) (i) is incorrect
(b) (ii) is incorrect
(c) (iii) is correct
(d) (iv) is incorrect
Answer:
(c) (iii) is correct

Question 7.
(i) Egypt was called as the Gift of Nile
(ii) Egyptians practiced polytheism
(iii) Thoth is the God of death
(iv) Cuneiform is Egyptian way of writing
(a) (i) & (ii) are incorrect
(b) (iii) & (iv) are correct
(c) (iii) is correct
(d) (i) & (ii) are correct
Answer:
(d) (i) & (ii) are correct

Question 8.
Confucius was famous among the Chinese Philosophers.
(a) Lao Tze
(b) Confucius
(c) Mencius
(d) Sun Tzu
Answer:
(b) Confucius

II. Fill in the blanks.

1. The River Nile originates in ……………
2. The preserved dead body is called …………….
3. …………. was the God of writing and learning.
4. The city of Akkad later became the city of ……………. a commercial and cultural centre of largest Asia.
5. …………. is perhaps the oldest written epic on earth.
6. ………….. was the popular ruler often late (or) neo Assyrian Empire.
7. ………….. was the first military power in History.
8. Agriculture was the main occupation of the …………..
9. The ……………. refers to the large collection of terracotta warrior images found in China.
10. The Indus Valley civilization is also known as ………….. civilization.
11. The Indus people worshipped …………… trees.
12. The Harappans had a close trade link with the ………………
Answers:
1. Lake Victoria
2. the mummy
3. Thoth
4. Babylon
5. The Epic of Gilgamesh
6. Ashurbanipal
7. Assyrian Empire
8. Mesopotamians
9. The Terracotta Army
10. Harappan
11. Pipal
12. Mesopotamians

III. Find out the correct statement.

Question 1.
(a) The oldest civilisation in Mesopotamia belonged to the Sumerians.
(b) The Sumerians believed to have originated from Central Asia.
(c) Sargon and his descendants ruled Mesopotamia for more than 200 years.
(d) The Akkadians dominated Sumeria briefly from 2500 BCE to 2450 BCE.
Answer:
(a) correct
(b) correct
(c) incorrect
(d) incorrect

Question 2.
(a) The Harappans used painted Pottery.
(b) The Harappans have no knowledge about weights and measures.
(c) The Indus people buried the dead.
(d) The Indus civilization completely disappeared.
Answer:
(a) correct
(b) incorrect
(c) correct
(d) incorrect

IV. Match the following.

Answer:
1. (d)
2. (a)
3. (e)
4. (b)
5. (c)

V. Answer the following briefly.

Question 1.
The term civilization is used to distinguish the Urban society from early forms of societies. Why?
Answer:

• The Urban society practised crafts, engaged in trade and exchange, adopted science and technology and formed political organisation.
• Hence the term civilisation is used to distinguish them from the early forms of societies.

Question 2.
What is Egyptian civilization known for?
As one of the oldest civilizations, the Egyptian civilisation is known for its monumental architecture, art, sciences and crafts at a very early age.

Question 3.
Mention the contributions of the Mesopotamian civilization.
Answer:

1. The invention of the potter’s the wheel is credited to the Sumerians.
2. They developed the calendar system of 360 days and divided a circle into 360 units.
3. The Cuneiform system of writing was their contribution.
4. Hammurabi’s law code was another legacy of the Mesopotamians.

Question 4.
Write a short note on “Silk Road” in China.
Answer:

1. The greatest of the Han emperors Wu Ti (Han Wu the Great, 141 to 87 BCE) sent Zhang Qian as emissary to the West in 138 BCE.
2. It paved the way for the opening of the Silk Road in 130 BCE to encourage trade activities.
3. Because of the Silk Road and the resultant trade connections, China benefitted immensely during the rule of Emperor Zhang.

Question 5.
The Indus civilisation is known as Harappan civilisation rather than Indus. Why?
Answer:

• The Indus valley civiliSation is also known as the Harappan civilisation since Harappa was the first site to be discovered.
• This civilisation is known as Harappan civilisation rather than Indus valley civilisation, since it extended beyond the Indus river valley.

VI. Answer all the questions given under each caption.

Question 1.
The Babylonians.
(i) Who were the Babylonians?
Answer:
The Semitic people called Amorites who moved from the Arabian desert into Mesopotamia were known as Babylonians

(ii) Name the oldest written epic on earth. .
Answer:
The Epic of Gilgamesh is the oldest written epic on earth.

(iii) Who was a great law-maker?
Answer:
Hammurabi the sixth king of Babylon was a great law-maker.

(iv) What was the previous name of Babylon?
Answer:
The previous name of Babylon was the city of Akkad.

Question 2.
Indus civilisation.
(i) What is the other name of Indus civilisation?
Answer:
The Harappan civilisation.

(ii) What did the Harappans use for construction?
Answer:
The Harappans used baked and unbaked bricks and stones for construction.

(iii) What kind of pottery was used by the Harappans?
Answer:
The Harappans used painted potteries. Their potteries have a deep red slip and black paintings.

(iv) What was their belief for the dead?
Answer:
The Indus people buried the dead. Burials were done elaborately.

VII. Answer the following in detail.

Question 1.
How did the Egyptians excel in art and architecture? Explain.
Answer:

1. The Egyptians excelled in art and architecture. Their writing is also, a form of art.
2. Numerous sculptures, paintings, and carvings attest to the artistic skills of Egyptians.
3. The pyramids are massive monuments built as tombs of mourning to the Pharaohs.
4. The great pyramids near Cairo are known as the Giza Pyramids.
5. Pyramids are considered to be one of the wonders of the world, and they were built between 2575 and 2465 BCE.
6. These monuments display the engineering, architectural and human resource management skills of the Egyptians.
7. The Great Sphinx of Giza is a massive limestone image of a lion with a human head.
8. It is dated to the time of Pharaoh Khaffe. It is one of the largest sculptures of the world and measures seventy-three metres in length and twenty metres in height.

Question 2.
Compare the Indus Civilization with Tamil Civilization.
Answer:
(i) The similarity of the graffiti found on the megalithic burial pots of South India with the Indus script and the identical place names of Tamil Nadu and the Indus region of Pakistan are presented as arguments to establish the relationship between the Indus civilisation and Tamil culture.

(ii) Researchers like Father Henry Heras, Asko Parpola and Iravatham Mahadevan find similarity between the Indus script and the Dravidian/Tamil language.

(iii) Archaeological evidence points out that several groups of people have been living in Tamil Nadu and South India continuously from the Mesolithic period.

(iv) A few groups from the Indus region might have migrated into southern India.

(v) Some of the ideas and technologies of the Indus civilisations had reached South India in the Iron Age.

(vi) The carnelian beads, shell bangles, and bronze mirrors found in the Megalithic/Early Historic sites of Tami Nadu were first introduced by the people of the Indus civilisation. More research is needed to arrive at any definite conclusion in this matter.

(vii) The towns of ancient Tamilagam such as Arikkamedu, Uraiyur and Keezhadi that flourished are part of the second urbanisation of India and these towns are much different from the Indus cities. These towns emerged approximately 1,200 years after the decline of the Indus civilisation.

You can Download Samacheer Kalvi 9th Social Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Social Science Economics Solutions Chapter 1 Understanding Development: Perspectives, Measurement and Sustainability

Understanding Development: Perspectives, Measurement and Sustainability Textual Exercise

I. Choose the correct answer.

Question 1.
Assertion (A): Development increases the quality of life.
Reason (R): People will have higher incomes, better education, better health and nutrition, less poverty. .
(a) Both (A) and (R) are true and (R) explains (A)
(b) Both (A) and (R) are true and (R) does not explain (A)
(c) (A) is correct and (R) is false
(d) (A) is false and (R) is true
Answer:
(a) Both (A) and (R) are true and (R) explains (A)

Question 2.
The term‘Human resources’ refers to ……
(a) investment on poor people
(b) expenditure on agriculture
(c) investment on assests
(d) collective abilities of people
Answer:
(d) collective abilities of people

Question 3.
For comparing development between countries, their …… is considered to be one of the
most important attributes.
(a) growth
(b) income
(c) expenditure
(d) savings
Answer:
(b) income

Question 4.
……. is considered a true measure of national income.
(a) GNP
(b) GDP
(c) NNP
(d) NDP
Answer:
(c) NNP

Question 5.
The …… income is also called per capita income.
(a) average
(b) total
(c) people
(d) monthly
Answer:
(a) average

Question 6.
Which one of the following country is not a G-8 country?
(a) Japan
(b) Canada
(c) Russia
(d) India
Answer:
(d) India

Question 7.
Which one of the following country is not a member of SAARC?
(a) India
(b) Pakistan
(c) China
(d) Bhutan
Answer:
(c) China

Question 8.
Assertion (A) : The Net Product (NNP) is considered as a true measure of national output.
Reason (R): It is also known as national income.
(a) Both (A) and (R) are true and (R) explains (A)
(b) Both (A) and (R) are true and (R) does not explain (A)
(c) (A) is correct and (R) is false
(d) (A) is false and (R) is true
Answer:
(a) Both (A) and (R) are true and (R) explains (A)

Question 9.
Assertion (A): Human resource is necessary for the progress of any country.
Reason (R): Investment in education and health of people can result in a high rate of returns in the future for a country.
(a) Both (A) and (R) are true and (R) explains (A)
(b) Both (A) and (R) are true and (R) does not explain (A)
(c) (A) is correct and (R) is false
(d) (A) is false and (R) is true
Answer:
(a) Both (A) and (R) are true and (R) explains (A)

Question 10.
The Human Development Index (HDI) does not take into account the following dimension in its calculation.
(a) Gender
(b) Health
(c) Education
(d) Income
Answer:
(a) Gender

Question 11.
Among the following states which state have the literacy rate (2011) higher than national average?
(a) Andhra Pradesh
(b) Uttar Pradesh
(c) Tamil Nadu
(d) None of these
Answer:
(c) Tamil Nadu

Question 12.
Sex-ratio means …..
(a) the ratio between adult-male and adult female in a population
(b) the ratio between female and male in a population
(c) the relationship between a male of female
(d) the number of females per thousand males
Answer:
(b) the ratio between female and male in a population

Question 13.
Inter-generational equality is ensured under the process of
(a) Industrial progress
(b) Economic development
(c) Sustainable development
(d) Economic growth
Answer:
(b) Economic development

Question 14.
Find the odd one.
(a) Solar energy
(b) Wind energy
(c) Paper
(d) Natural gas
Answer:
(c) Paper

Question 15.
……….. is the state with the highest installed solar capacity in India.
(a) Tamil Nadu
(b) West Bengal
(c) Kerala
(d) Andhra Pradesh
Answer:
(a) Tamil Nadu

Question 16.
……. resources are those which will get exhausted after years of use.
(a) Natural
(b) Renewable
(c) Non-Renewable
(d) New
Answer:
(c) Non-Renewable

Question 17.
The thermal plant emits a large quantity of ……, which pollutes the environment.
(a) Oxygen
(b) Nitrogen
(c) Carbon
(d) Carbon dioxide
Answer:
(d) Carbon dioxide

II. Fill in the blanks

1. The economic progress of any country is known as ………
2. The head quarters of the HRD Ministry is in ……..
3. The state has the highest literacy rate in India is ……….
4. Human Development Report of the world prepared and released by …….
5. Groundwater is an example of ……. resource.
6. The book An Uncertain Glory was written by ……..

Answers:

1. economic development
2. New Delhi
3. Kerala
4. UNDP
5. renewable
6. Prof. Amartya Sen

III. Match the following

Answers:
1. (d)
2. (c)
3. (b)
4. (a)

IV. Give Short Answers

Question 1.
What do you mean by development?
Answer:

1. Development refers to the progress in a particular field or particular person.
2. Similarly, by the economic progress of a country, it is known as economic development.
3. However, the interpretation of the concept development keeps on changing from time to time, from person to person.
4. Its meaning gets extended further.

Question 2.
What are the indicators of development?
Answer:
The major indicators to measure the level of economic development are Net National Product (NNP), Per Capita Income (PCI), Purchasing Power Parity (PPP), and Human Development
Index (HDI).

Question 3.
Why NNP is not considered as a useful measure to compare a country’s development with other countries?
Answer:

1. For comparison between countries’ development, total income or the national income is not a useful measure.
2. Since countries have different populations, comparing total income will not tell us what an average person is likely to earn.
3. Hence we compare average income which is also called per capita income.
4. Now the economy has realised that investment in human capital

Question 4.
Why human resources is considered the foremost resource of any country?
Answer:

1. Human Resource is necessary for the progress of any country.
2. ‘Human Resources’ refers to the collective abilities of people, which can be utilised in the production sector.

So human resource is considered as the foremost resource of any country.

Question 5.
Expand the following:
1. PPP
2. HDI
Answer:
1. PPI – Purchasing Power Parity
2. HD – Human Development Index.

Question 6.
Expand the following:
1. NNP
2. PCI.
Answer:
1. NNP – Net National Product
2. PCI – Per Capita Income

Question 7.
What is‘Solar Power’?
Answer:
Solar power is the conversion of energy from sunlight into electricity either directly using photovoltaic cells or indirectly using concentrated solar power. Solar panels absorb sunlight as a source of energy to generate electricity.

V. Answer in detail.

Question 1.
Discuss the policies for sustainable development.
Answer:

1. Sustainable economic development means development should take place without damaging the environment. Sustainability
2. The development in the present should not compromise with the needs of the future generation.
3. Sustainability of development is comparatively a new era of knowledge in which scientists, economists, philosophers, and other social scientists are working together.
4. If the environment is not protected, we fall prey to national disaster.
5. To achieve time sustainability we need to balance economic social and environmental sustainability in equal harmony.
6. In general, the question of development or process is perennial.

Question 2.
Describe in detail environmental policies in India.
Answer:
Environmental policies in India:

1. Environmental policies in India have been evolved considerably over the past 3 decades.
2. These policies have covered a wide range of issues such as air, water pollution, waste management, and biodiversity conservation.
3. India faces challenges in economic development, which is to be met from limited resources and uncertain climate.
4. One of the approaches to overcome this challenge is through the path of sustainable development.
5. The Supreme Court of India has been engaged in interpreting and introducing new changes in Environmental protection.
6. Article 51 A(g) of the Constitution states that “It shall be the duty of every citizen of India to protect and improve the natural environment including forests, lakes, rivers, and wildlife and to have compassion for living creatures.”
7. The Indian Wildlife Protection Act of 1972 protected biodiversity.
8. The 1988 National Forest Policy had conservations as its fundamental principle.
9. The Government passed the Environment Protection Act in 1986.
10. Foreign Trade (Development and Regulation) Act of 1992 for control of bio-diversity.
11. Development increases with the quality of life.
12. People will have higher incomes, better education, better health and nutrition, less poverty, and more equality of opportunity.

Question 3.
Differentiate between renewable and non-renewable resources.
Answer:

Question 4.
Mention any five environmental acts and their action.
Answer:

VI. Projects and Activities.

List the various ways in which the problems of garbage and emissions are being dealt with around the world.
Answer:

1. The threat of waste to the environment’s health and safety is huge.
2. Pollution runs into rivers and seeps into groundwater.
3. Flooding is caused by garbage clogging drains and the atmosphere can be poisoned by the toxic discharge from the trash.
4. Bacteria, insects, and vermin thrive from garbage, causing pollution leading to respiratory diseases, contamination of surface-water affecting all eco-system.
5. We can reduce waste at home by knowing the rules of recycling, ditching plastic bags, learning to repair rather than discarding, not using disposable plates, etc.
6. Use environmentally safe products, use water-based paints, dispose of trash properly.

VII. HOTS

Write in detail what kind of environmental problems you face in your locality.
Location: Velachery – Chennai.
Problem: “Despite being one of the fastest-growing localities with several upmarket malls and hotels living in Velachery still face basic problems such as

1. Overflowing sewage
2. Poor drainage
3. The underground water-breeding grounds for mosquitoes.
4. There is always the fear of contamination of drinking water.
5. every time it pours in the city, most of Velachery drowns.

The above-mentioned problems are the dominant ones in Velachery.

VIII. Life Skill.

Question 1.
How is the Per Capita income calculated?
Answer:

1. Per capita income is the average income of an individual of a country
2. It is calculated by dividing the area’s total income by its total population.

PCI – Per = \(\frac { NNP }{ Total Population of country }\)
PCI – Per Capita Income; NNP – Net National Product.

Understanding Development: Perspectives, Measurement, and Sustainability Additional Questions

I. Choose the correct answer.

Question 1.
Assertion (A): The term ‘economic development’ refers to the overall growth of all sectors of
the economy.
Reason (R): By adoption of new technologies.
(a) Both (A) and (R) are true and (R) explains (A)
(b) Both (A) and (R) are true and (R) does not explain (A)
(c) (A) is correct and (R) is false
(d) (A) is false and (R) is true
Answer:
(a) Both (A) and (R) are true and (R) explains (A)

Question 2.
This is also known as National Income.
(a) NNP
(b) GDP
(c) PCI
(d) PPP
Answer:
(a) NNP

Question 3.
This is not a G8 country.
(a) Russia
(b) Canada
(c) France
(d) Nepal
Answer:
(d) Nepal

Question 4.
This is one of the ‘BRICS’ countries.
(a) China
(b) Afghanistan
(c) Nepal
(d) Pakistan
Answer:
(a) China

Question 5.
The enrolment for higher education in the highest in ……… in India.
(a) Kerala
(b) Tamil Nadu
(e) West Bengal
(d) Maharashtra
Answer:
(b) Tamil Nadu

Question 6.
This is a renewable resource.
(a) Metals
(b) Glass
(c) Wind energy
(d) Diesel
Answer:
(c) Wind energy

II. Fill in the blanks.

1. Every human being has an ……… of his (or) her own to achieve progress in life.
2. Countries with higher income are considered to be ………
3. ……… became the third-largest economy in terms of PPP.
4. …….. can be divided into renewable resources and non-renewable resources.
5. ……. absorb the sunlight as a source of energy to generate electricity.

Answers:

1. Ambition
2. More developed
3. India
4. Natural resources
5. Solar panels

III. Match the following

Answer:
1. (d)
2. (a)
3. (b)
4. (c)

IV. Give short answers.

Question 1.
What leads to development?
Answer:
If our thinking turns towards progress and about the ways to achieve the many goals for progress, it leads to development.

Question 2.
For comparing the development of various countries, total income is not a useful measure. How?
Answer:
Since the countries have different populations comparing total income will not be suggestive of what an average person is likely to earn. So, for comparing the development of various countries total income is not a useful measure.

Question 3.
Define Purchasing Power Parity.
Answer:
Purchasing Power Parity is defined as the number of units of a country’s currency required to buy the same amount of goods and services in the domestic market as one dollar would buy in the U.S.

Question 4.
What do you mean by Human Resource Development?
Answer:
Human Resource Development means the development of a person’s physical and mental abilities through education, health care, and training.

Question 5.
Why do we say that investment in education and health of people can result in a high rate
of returns?
Answer:
If a child is invested with good education and health, he or she may turn to be very productive in the future in the form of higher earnings and greater contribution to society. Therefore, investment in education and health of people can result in a high rate of returns

Question 6.
What is the end result of Development?
Answer:

1. Development increases the quality of life.
2. People will have higher incomes, better education, better health and nutrition, less poverty and more equality of opportunity.

V. Answer in detail.

Question 1.
Describe the sustainability of Development.
Answer:
Sustainable economic development is taken to mean development without damaging the environment and not compromising with the needs of the future generation.

The consequences of environmental degradation do not respect national or state boundaries. Sustainability of development is comparatively a new area of knowledge in which scientists, economists, philosophers, and other social scientists are working together.

Natural resources can be divided into renewable resources and non-renewable resources.
Groundwater is an example of a renewable resource. The question arises as to how sustainable development is possible if the resources are over-used rather than getting replenished. Non-renewable resources get exhausted after a certain number of years of extracting and using them and they cannot be replenished.

To achieve real sustainability, we need to balance economic, social, and environmental sustainability in equal harmony.

In general, the question of development or progress is continuous. At all times, as a member of society and as individuals, we need to ask where we want to go, what we wish to become and what our goals are.

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.4

Question 1.
By the principle of mathematical induction, prove that, for n ≥ 1

Solution:

∴ P(k+ 1) is true.
Thus P(K) is true ⇒ (k + 1) is true.
Hence by principle of mathematical induction, P(n) is true for all n ∈ N.

Question 2.
By the principle of mathematical induction, prove that, for n > 1

Solution:

∴ P(1) is true
Let P(n) be true for n = k

∴ P(k + 1) is true
Thus P(k) is true ⇒ P(k + 1) is true. Hence by the principle of mathematical induction, P(k) is true for all n ∈ N.

Question 3.
Prove that the sum of the first n non-zero even numbers is n² + n.
Solution:
Let P(n) = 2 + 4 + 6 + ………….. + 2n = n² + n

Step 1:
Let us verify the statement for n = 1
P (1 ) = 2 = 1² + 1 = 1 + 1 = 2.
∴ The given result is true for n = 1.

Step 2:
Let us assume that the given result is true for n = k
P ( k) = 2 + 4 + 6 + ………… + 2k = k² + k

Step 3:
Let us prove the result for n = k + 1
P (k+ 1 ) = 2 + 4 + 6+ + 2k + (2k + 2 )
P(k+ 1 ) = P(k) + (2k + 2)
= k² + k + 2k + 2
= k² + 3k + 2
= k² + 2k + k + 2
= k(k +2) + 1(k + 2)
P(k+ 1 ) = (k+ 1) (k + 2) ……….. (1)
P (k) = k² + k
= k (k + 1 )
P(k+ 1) = (k + 1) (k + 1 + 1)
= (k + 1) (k + 2)
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
2 + 4 + 6 + ………….. + 2n = n² + n
is true for all natural numbers n.

Question 4.
By the principle of Mathematical induction, prove that, for n ≥ 1.

Solution:


∴ P(k + 1) is true
Thus P(k) is true ⇒ P(k + 1) is true
Hence by the principle of mathematical induction, P(n) is true for all n ∈ N

Question 5.
Using the Mathematical induction, show that for any natural number n ≥ 2,

Solution:


⇒ P(k + 1) is true when P(k) is true so by the principle of mathematical induction P(n) is true.

Question 6.
Using the Mathematical induction, show that for any natural number n ≥ 2,

Solution:


⇒ P(k + 1) is true when P(k) is true so by the principle of mathematical induction P(n) is true for n ≥ 2.

Question 7.
Using the Mathematical induction, show that for any natural number n

Solution:


∴ P(k + 1) is true
Thus p(k) is true ⇒ P(k + 1) is true
Hence by the principle of mathematical induction,
p(n) is true for all n ∈ z

Question 8.
Using the Mathematical induction, show that for any natural number n,

Solution:


∴ P(k + 1) is true
Thus P(k) is true ⇒ P(k + 1) is true. Hence by the principle of mathematical induction, P(n) is true for all n ∈ N.

Question 9.
Prove by Mathematical Induction that
1! + (2 × 2!) + (3 × 3!) + … + (n × n!) = (n + 1)! – 1
Solution:
Let p(n) = 1! + (2 × 2 !) + (3 × 3!) +…. .+ (n × n!) = (n + 1)! – 1

Step 1:
First let us verify the result for n = 1
P(1) = 1! = (1 + 1)! – 1
P(1) = 1! = 2! – 1
P(1) = 1 = 2 – 1 = 1
∴ We have verified the result for n = 1.

Step 2:
Let us assume that the result is true for n = k
P(k) = (1 × 1 !) + (2 × 2!) + (3 × 3!) + …………. + (k × k!) = (k + 1)! – 1

Step 3:
Let us prove the result for n = k + 1
P(k + 1)=(1 × 1!) + (2 × 2!) + (3 × 3!) + ………….. + (k × k!) + ((k + 1) × (k + 1)!)
P(k + 1) = P(k) + ((k + 1) × (k + 1)!)
P(k + 1) = (k + 1)! – 1 + (k + 1) × (k + 1)!
= (k + 1)! + (k + 1) (k + 1)! – 1
= (k + 1)! (1 + k + 1) – 1
= (k + 1)! (k + 2) – 1
= (k + 2)! – 1
P(k + 1) = ((k + 1) + 1)! – 1
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
(1 × 1!) + (2 × 2!) + (3 × 3!) + …………… + (n × n!) = (n + 1)! – 1
is true for all natural numbers n.

Question 10.
Using the Mathematical induction, show that for any natural number n, x²ⁿ – y²ⁿ is divisible by x +y.
Solution:
Let P(n) = x²ⁿ – y²ⁿ is divisible by x + y
Step 1:
First, let us verify the result for n = 1.
P ( 1 ) = x²⁽¹⁾ – y²⁽¹⁾ = x² – y²
P(1) = (x + y) (x – y) which is divisible by x + y
∴ The result is true for n = 1

Step 2:
Let us assume that the result is true for n = k
P(k) = x^2k – y^2k which is divisible by x + y
∴ P (k) = x^2k – y^2k = λ (x + y) where λ ∈ N ——— (1)

Step 3:
Let us prove the result for n = k + 1

∴ P ( k + 1) is divisible by x + y
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
x²ⁿ – y²ⁿ is divisible by x + y
for all natural numbers n.

Question 11.
By the principle of mathematical induction, prove that, for n ≥ 1,

Solution:

Question 12.
Use induction to prove that n³ – 7n + 3, is divisible by 3, for all natural numbers n.
Solution:
Let P ( n) = n³ – 7n + 3 is divisible by 3

Step 1:
First let us verify the results for n = 1
P(I) = 1³ – 7 × 1 + 3
= 1 – 7 + 3
P (1) = – 3
which is divisible by 3
∴ The result is true for n = 1

Step 2:
Let us assume that the result is true for n = k
P(k) = k³ – 7k + 3 is divisible by 3
P(k) = k³ – 7k + 3 = 3λ where λ ∈ N

Step 3:
Let us prove the result for n = k + 1
P(k + 1) = (k + 1)³ – 7(k + 1 ) + 3
= k³ + 3k² + 3k + 1 – 7k – 7 + 3
= k³ + 3k² – 4k – 3
= k³ – 4k – 3k + 3k – 3 + 6 – 6 + 3k²
= k³ – 7k + 3 + 3k – 6 + 3k²
= (k³ – 7k + 3) + 3(k² + k – 2)
= 3λ + 3 (k² + k – 2)
P(k + 1) = 3 (λ + k² + k – 2 )
which is a multiple of 3, hence divisible by 3
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
n³ – 7n + 3 is divisible by 3 for all natural numbers n.

Question 13.
Use induction to prove that 5^{n + 1} + 4 × 6ⁿ when divided by 20 leaves a remainder 9, for all natural numbers n.
Solution:
P(n) is the statement 5^{n + 1} + 4 × 6ⁿ – 9 is ÷ by 20
P(1) = 5^{1 + 1} + 4 × 6¹ – 9 = 5² + 24 – 9
= 25 + 24 – 9 = 40 ÷ by 20
So P(1) is true
Assume that the given statement is true for n = k
(i.e) 5^{k + 1} + 4 × 6ⁿ – 9 is ÷ by 20
P(1) = 5^{1 + 1} + 4 × 6¹ – 9
= 25 + 24 – 9
So P(1) is true
To prove P(k + 1) is true
P(k + 1) = 5^{k + 1 + 1} + 4 × 6^{k + 1 + 1} – 9
= 5 × 5 ^{k + 1} + 4 × 6 × 6^k – 9
= 5[20C + 9 – 4 × 6^k] + 24 × 6^k – 9 [from(1)]
= 100C + 45 – 206^k + 246^k – 9
= 100C + 46^k + 36
= 100C + 4(9 + 6^k)
Now for k = 1 ⇒ 4(9 + 6^k) = 4(9 + 6)
= 4 × 15 = 60 ÷ by 20 .
for k = 2 = 4(9 + 6²) = 4 × 45 = 180 ÷ 20
So by the principle of mathematical induction 4(9 + 6^k) is ÷ by 20
Now 100C is ÷ by 20.
So 100C + 4(9 + 6^k) is ÷ by 20
⇒ P(k + 1) is true whenever P(k) is true. So by the principle of mathematical induction P(n) is true.

Question 14.
Use induction to prove that 10ⁿ + 3 × 4^{n + 2} + 5, is divisible by 9, for all natural numbers n.
Solution:
P(n) is the statement 10ⁿ + 3 × 4^{n + 2} + 5 is ÷ by 9
P(1) = 10¹ + 3 × 4² + 5 = 10 + 3 × 16 + 5
= 10 + 48 + 5 = 63 ÷ by 9
So P(1) is true. Assume that P(k) is true
(i.e.) 10^k + 3 × 4^{k + 2} + 5 is ÷ by 9
(i.e.) 10^k + 3 × 4^{k + 2} + 5 = 9C (where C is an integer)
⇒ 10^k = 9C – 5 – 3 × 4^{k + 2} ……(1)
To prove P(k + 1) is true.
Now P(k + 1) = 10^{k + 1} + 3 × 4^{k + 3} + 5
= 10 × 10^k + 3 × 4^{k + 2} × 4 + 5
= 10[9C – 5 – 3 × 4^{k + 2}] + 3 × 4^{k + 2} × 4 + 5
= 10[9C – 5 – 3 × 4^{k + 2}] + 12 × 4^{k + 2} + 5
= 90C – 50 – 30 × 4^{k + 2} + 12 × 4^{k + 2} + 5
= 90C – 45 – 18 × 4^{k + 2}
= 9[10C – 5 – 2 × 4^{k + 2}] which is ÷ by 9
So P(k + 1) is true whenever P(K) is true. So by the principle of mathematical induction P(n) is true.

Question 15.
Prove that using the Mathematical induction

Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.4 Additional Questions

Question 1.
Prove by induction the inequality (1 + x)ⁿ ≥ 1 + nx, whenever x is positive and n is a positive integer.
Solution:
P(n) : (1 +x)ⁿ ≥ 1 +nx
P(1): (1 + x)¹ ≥ 1 + x
⇒ 1 + x ≥ 1 + x, which is true.
Hence, P(1) is true.
Let P(k) be true
(i.e.) (1 + x)^k ≥ 1 + kx
We have to prove that P(k + 1) is true.
(i.e.) (1 + x)^{k + 1} ≥ 1 + (k + 1)x
Now, (1 + x)^{k + 1} ≥ 1 + kx [∵ p(k) is true]
Multiplying both sides by (1 + x), we get
(1 + x)^k(1 + x) ≥ (1 + kx)(1 + x)
⇒ (1 + x)^{k + 1} ≥ 1 + kx + x + kx²
⇒ (1 + x)^{k + 1} ≥ 1 + (k + 1)x + kx² ….. (1)
Now, 1 + (k + 1) x + kx² ≥ 1 + (k + 1)x …… (2)
[∵ kx² > 0]
From (1) and (2), we get
(1 + x)^{k + 1} ≥ 1 + (k + 1)x
∴ P(k + 1) is true if P(k) is true.
Hence, by the principle of mathematical induction, P(n) is true for all values, of n.

Question 2.
3²ⁿ – 1 is divisible by 8.
Solution:
P(n) = 3²ⁿ – 1 is divisible by 8
For n = 1, we get
P(1) = 3^2.1 – 1 = 9 – 1 = 8
P(1) = 8, which is divisible by 8.
Let P(n) be true for n = k
P(k) = 3^2k – 1 is divisible by 8 ….. (1)
Now, P(k + 1) = 3^{(2k + 2)} – 1 = 3^2k.3² – 1
= 3²(3^2k – 1) + 8
Now, 3^2k – 1 is divisible by 9. [Using (1)]
∴ 3² (3^2k – 1) + 8 is also divisible by 8.
Hence, 3²ⁿ – 1 is divisible by 8 ∀ n E N

Question 3.
Prove by the principle of mathematical induction if x and y are any two distinct integers, then xⁿ – yⁿ is divisible by x – y. [OR]
xⁿ – yⁿ is divisible by x – y, where x – y ≠ 0.
Solution:
Let the given statement be P(n).
(i.e.) P(n): xⁿ – yⁿ = M(x – y), x – y ≠ 0

Step I.
When n = 1,
xⁿ – yⁿ = x – y = M(x – y) ….(1)
⇒ P(1) is true.

Step II.
Assume that P(k) is true.
(i.e.) x^k – y^k = M(x – y), x – y ≠ 0
We shall now show that P(k + 1) is true
Now, x^{k + 1} – y^{k + 1} = x^{k + 1} – x^ky + x^{k + 1}y – y^{k + 1}
= x^k(x – y) + y(x^k – y^k)
= x^k(x – y) + yM(x – y) [Usng ….. (1)]
= (x – y)(x^k – yM)
∴ By the principle of mathematical induction, P(n) is true for all n ∈ N

Question 4.
Prove by the principle of mathematical induction that for every natural number n, 3^{2n + 2} – 8n – 9 is divisible by 8.
Solution:
Let P(n): 3^{2n + 2} – 8n – 9 is divisible by 8.
Then, P(1): 3^{2.1 + 2} – 8.1 – 9 is divisible by 8.
(i.e.) 3⁴ – 8 – 9 is divisible by 8 or 81 – 8 – 9 is divisible by 8
(or) 64 is divisible by 8, which is true.
Suppose P(k) is true, then
P(k) : 3^{2k + 2} – 8k – 9 is divisible by 8
(i.e.) 3^{2k + 2} – 8k – 9 = 8m, where m ∈ N (or)
3^{2k + 2} = 8m + 8k + 9
P(k + 1) is the statement given by, …(1)
P(k + 1) : 3^{2(k + 1) + 2} – 8(k + 1) – 9

∴ P(k + 1) is true
Hence, by the principle of mathematical induction, P(n) is true for all n ∈ N

Question 5.
Use the principle of mathematical induction to prove that for every natural number n.

Solution:
Let P(n) be the given statement, i.e.

⇒ P(1) is true.
We note that P(n) is true for n = 1.
Assume that P(k) is true

Now, we shall prove that P(k + 1) is true whenever P(k) is true. We have,

∴ P(k + 1) is also true whenever P(k) is true
Hence, by the principle of mathematical induction, P(n) is also true for all n ∈ N.

Question 6.
n³ – n is divisible by 6, for each natural number n ≥ 2.
Solution:
Let P(n) : n³ – n

Step 1 :
P(2): 2³ – 2 = 6 which is divisible by 6. So it is true for P(2).

Step 2 :
P(A): k³ – k = 6λ. Let it is be true for k ≥ 2
⇒ k³ = 6λ + k …(i)

Step 3 :
P(k + 1) = (k + 1)³ – (k + 1)
= k³ + 1 + 3k² + 3k – k – 1 = k³ – k + 3(k² + k)
= k³ – k + 3(k² + k) = 6λ + k – k + 3(k² + k)
= 6λ + 3(k² + k) [from (i)]
We know that 3(k² + k) is divisible by 6 for every value of k ∈ N.
Hence P(k + 1) is true whenever P(k) is true.

Question 7.
For any natural number n, 7ⁿ – 2ⁿ is divisible by 5.
Solution:
Let P(n) : 7ⁿ – 2ⁿ

Step 1:
P(1) : 7¹ – 2¹ = 5λ which is divisible by 5. So it is true for P(1).

Step 2:
P(k): 7^k – 2^k = 5λ. Let it be true for P(k)

Step 3:
P(k + 1) = 7^{k + 1} – 2^{k + 1}

So, it is true for P(k + 1)
Hence, P(k + 1) is true whenever P(k) is true.

Question 8.
n² < 2ⁿ, for all natural numbers n ≥ 5.
Solution:
Let P(n) : n² < 2ⁿ for all natural numbers, n ≥ 5

Step 1 :
P(5) : 1⁵ < 2⁵ ⇒ 1 < 32 which is true for P(5)

Step 2 :
P(k): k² < 2k. Let it be true for k ∈ N

Step 3 :
P(k + 1): (k + 1)² < 2^{k + 1}
From Step 2, we get k² < 2^k
⇒ k² < 2^{k + 1} < 2k + 2k + 1


From eqn. (i) and (ii), we get (k + 1)² < 2^{k + 1}
Hence, P(k + 1) is true whenever P(k) is true for k ∈ N, n ≥ 5.

Question 9.
In 2n < (n + 2)! for all natural number n.
Solution:
Let P(n) : 2n < (n + 2)! for all k ∈ N.

Hence, P(k + 1) is true whenever P(k) is true.

Question 10.
1 + 5 + 9 + … + (4n – 3) = n(2n – 1), ∀ n ∈ N.
Solution:
Let P(n) : 1 + 5 + 9 + … + (4n – 3) = n(2n – 1), ∀ n ∈ N

Step 1:
P(1) : 1 = 1(2.1 – 1) = 1 which is true for P(1)

Step 2:
P(k) : 1 + 5 + 9 + … + (4k – 3) = k(2k – 1). Let it be true.

Step 3:
P(k + 1) : 1 + 5 + 9 + … + (4k – 3) = k(4k + 1)
= k(2k – 1) + (4k + 1) = 2k² – k + 4k + 1
= 2k² + 3k + 1 = 2k² + 2k + k + 1
= 2k(k + 1) + 1 (k + 1) = (2k + 1)(k + 1)
= (k+ 1) (2k + 2 – 1) = (k + 1) [2(k + 1) – 1]
Which is true for P(k + 1).
Hence, P(k + 1) is true whenever P(k) is true.

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets Ex 1.3

Question 1.
Suppose that 120 students are studying in 4 sections of eleventh standard in a school. Let A denote the set of students and B denote the set of the sections. Define a relation from A to B as “x related toy if the student x belongs to the section y”. Is this relation a function? What can you say about the inverse relation? Explain your answer.
Solution:
(i) A = {set of students in 11^th standard}
B = {set of sections in 11sup>th standard}
R : A ➝ B ⇒ x related to y
⇒ Every students in eleventh Standard must in one section of the eleventh standard.
⇒ It is a function.
Inverse relation cannot be a function since every section of eleventh standard cannot be related to one student in eleventh standard.

Question 2.
Write the values of f at – 4, 1, -2, 7, 0 if

Solution:
f(-4) = -(-4) + 4 = 8
f(1) = 1 – 1² = 0
f(-2) = (-2)² – (-2) = 4 + 2 = 6
f(7) = 0
f(0) = 0

Question 3.
Write the values of f at -3, 5, 2, -1, 0 if

Solution:
f(-3) = (-3)² – 3 – 5 = 9 – 8 = 1
f(5) = (5)² + 3(5) – 2 = 25 + 15 – 2 = 38
f(2) = 4 – 3 = 1
f(-1) = (-1)² + (-1) – 5 = 1 – 6 = -5
f(0) = 0 – 3 = -3

Question 4.
State whether the following relations are functions or not. If it is a function check for one-to-oneness and ontoness. If it is not a function, state why?
(i) If A = {a, b, c] and/= {(a, c), (b, c), (c, b)};(f: A ➝ A).
(ii) If X = {x, y, z} and/= {(x, y), (x, z), (z, x)}; (f: X ➝ X).
Solution:
(i) f : A ➝ A

It is a function but it is not 1 – 1 and not onto function.

(ii) f : X ➝ X

x ∈ X (Domain) has two images in the co-domain x. It is not a function.

Question 5.
Let A = {1, 2, 3, 4} and B = {a, b, c, d}. Give a function from A ➝ B for each of the following:
(i) neither one-to-one nor onto.
(ii) not one-to-one but onto.
(iii) one-to-one but not onto.
(iv) one-to-one and onto.
Solution:
A = {1, 2, 3, 4}
B = {a, b, c, d}.

R = {(1, b) (2, b) (3, c) (4, d)} is not 1-1 and not onto

(iii) Not possible

(iv)

Question 6.
Find the domain of \(\frac{1}{1-2 \sin x}\)
Solution:

Question 7.
Find the largest possible domain of the real valued function f(x) = \(\frac{\sqrt{4-x^{2}}}{\sqrt{x^{2}-9}}\)
Solution:

∴ No largest possible domain
The domain is null set

Question 8.
Find the range of the function \(\frac{1}{2 \cos x-1}\)
Solution:
The range of cos x is – 1 to 1

Question 9.
Show that the relation xy = -2 is a function for a suitable domain. Find the domain and the range of the function.
Solution:
(i) Let f: R → R defined as f: x → \(-\frac{2}{x}\) then
f(x) = \(-\frac{2}{x}\) or y = \(-\frac{2}{x}\)
⇒ xy = – 2
f (x) is not a function since f(x) is not defined for x = 0

(ii) Let f: R – {0} → R defined as f(x) = \(-\frac{2}{x}\)
⇒ y = \(-\frac{2}{x}\) = xy = – 2
f is one – one but not onto because 0 has no preimage.
f : R – {0} → R {0} is a function which is one- one and onto
Domain = R – {0}
Range = R – {0}

Question 10.
If f, g : R ➝ R are defined by f(x) = |x| + x and g(x) = |x| – x, find gof and fog.
Solution:

Question 11.
If f, g, h are real-valued functions defined on R, then prove that
(f + g)oh = foh + goh. What can you say about fo(g + h)? Justify your answer.
Solution:
Let f + g = k

= (f + g((h(x))
= f[h(x)] + g [h(x)]
= foh + goh
(i.e.,)(f + g)(o)h = foh + goh
fo(g + h) is also a function

Question 12.
If f: R ➝ R is defined by f(x) = 3x – 5, prove that f is a bijection and find its inverse.
Solution:
P(x) = 3x – 5
Let y = 3x – 5 ⇒ 3x = y + 5

Question 13.
The weight of the muscles of a man is a function of his bodyweight x and can be expressed as W(x) = 0.35x. Determine the domain of this function.
Solution:
Given W(x) = 0.35x
W(0) = W(1) = 0.35, W(2) = 0.7 ………….. W ( ∞ ) = ∞
Since x. denotes the bodyweight of a man, it will take only positive integers. That is x > 0.
W(x) : (0, ∞) → (0, ∞)
Domain = (0, ∞) , Range = (0, ∞)

Question 14.
The distance of an object falling is a function of time t and can be expressed as s(t) = -16t². Graph the function and determine if it is one-to-one.
Solution:
s(t) = -16t²
Suppose S(t₁) = S(t₂)

since time cannot be negative, we to take t₁ = t₂
Hence it is one-one.

t	0	1	2	3
s	0	-16	-64	-144

Question 15.
The total cost of airfare on a given route is comprised of the base cost C and the fuel surcharge S in rupee. Both C and S are functions of the mileage m; C(m) = 0.4m + 50 and S(m) = 0.03m. Determine a function for the total cost of a ticket in terms of the mileage and find the airfare for flying 1600 miles.
Solution:
Given the cost of airfare function and fuel surcharge functions are as follows.
C(m) = 0.4 m+ 50 ———- (1)
S (m) = 0.03 m ———- (2)
Total cost of a ticket = C(m) + S(m)
f(x) = 0.4 m + 50 + 0.03 m
f(x) = 0.43 m + 50
Given m = 1600 miles
The cost of Airfare for flying 1600 miles
f( 1600 ) = 0.43 × 1600 + 50
= 688 + 50
= 738
∴ Airfare for flying 1600 miles is Rs. 738.

Question 16.
A salesperson whose annual earnings can be represented by the function A(x) = 30, 000 + 0.04x, where x is the rupee value of the merchandise he sells. His son is also in sales and his earnings are represented by the function S(x) = 25, 000 + 0.05x. Find (A + S)(x) and determine the total family income if they each sell Rupees 1,50,00,000 worth of merchandise.
Solution:
A(x) = 30, 000 + 0.04x, where x is merchandise rupee value
S(x) = 25000 + 0.05 x
(A + S) (x) = A(x) + S(x)
= 30000 + 0.04x + 25000 + 0.05 x
= 55000 + 0.09x
(A + S) (x) = 55000+ 0.09x
They each sell x = 1,50,00,000 worth of merchandise
(A + S) x = 55000 + 0.09 (1,50,00,000)
= 55000 + 13,50,000
∴ Total income of family = ₹ 14,05,000

Question 17.
The function for exchanging American dollars for Singapore Dollar on a given day is f(x) = 1.23x, where x represents the number of American dollars. On the same day, the function for exchanging Singapore Dollar to Indian Rupee is g(y) = 50.50y, where y represents the number of Singapore dollars. Write a function which will give the exchange rate of American dollars in terms of the Indian rupee.
Solution:
f(x) = 1. 23x where x is number of American dollars.
g(y) = 50.50y where y is number of Singapore dollars.
gof(x) = g(f(x))
= g(1. 23x)
= 50.50 (1.23x)
= 62.115 x

Question 18.
The owner of a small restaurant can prepare a particular meal at a cost of Rupees 100. He estimates that if the menu price of the meal is x rupees, then the number of customers who will order that meal at that price in an evening is given by the function D(x) = 200 – x. Express his day revenue, total cost and profit on this meal as functions of x.
Solution:
Number of customers = 200 – x
Cost of one meal = Rs. 100
Cost of (200 – x) meals = (200 – x) × 100
Menu price of the meal = Rs. x
∴ Total menu price of (200 – x) meals = (200 – x) x
Profit = Menu price – Cost
= (200 – x) x – (200 – x) 100
Profit = (200 – x) (x – 100)

Question 19.
The formula for converting from Fahrenheit to Celsius temperatures is \(y=\frac{5 x}{9}-\frac{160}{9}\)
Find the inverse of this function and determine whether the inverse is also a function.
Solution:

Question 20.
A simple cipher takes a number and codes it, using the function f(x) = 3x – 4. Find the inverse of this function, determine whether the inverse is also a function and verify the symmetrical property about the line y = x (by drawing the lines).
Solution:
f(x) = 3x – 4
Let y = 3x – 4

Samacheer Kalvi 11th Maths Solutions Chapter 1 Sets Ex 1.3 Additional Questions

Question 1.
Find the domain and range of the function \(f(x)=\frac{1}{\sqrt{x-5}}\)
Solution:
Given that : f(x) \(f(x)=\frac{1}{\sqrt{x-5}}\)
Here, it is clear that / (x) is real when x – 5 > 0 ⇒ x > 5
Hence, the domain = (5, ∞)
Now to find the range put

For x ∈ (5, ∞), y ∈ R⁺.
Hence, the range of f = R⁺.

Question 2.
If \(f(x)=\frac{x-1}{x+1}\), then show that

Solution:

Question 3.
Find the domain of each of the following functions given by:
\(f(x)=\frac{x^{3}-x+3}{x^{2}-1}\)
Solution:

Here, f(x) is not defined if x² – 1 ≠ 0
(x – 1) (x + 1) ≠ 0
x ≠ 1, x ≠ -1
Hence, the domain of f = R – {-1, 1}

Question 4.
Find the range of the following functions given by
f(x) = 1 + 3 cos 2x
Solution:
Given that: f(x) = 1 + 3 cos 2x
We know that -1 ≤ cos 2x ≤ 1
⇒ -3 ≤ 3 cos 2x ≤ 3 ⇒ -3 + 1 ≤ 1 + 3 cos 2x ≤ 3 + 1
⇒ -2 ≤ 1 + 3 cos 2x ≤ 4 ⇒ -2 ≤ f(x) ≤ 4
Hence the range of f = [-2, 4]

Question 5.
Find the domain and range of the function \(f(x)=\frac{x^{2}-9}{x-3}\)
Solution:

Domain off: Clearly f(x) is not defined for x – 3 = 0 i.e. x = 3.
Therefore, Domain (f) = R – {3}
Range off: Let f(x) = y. Then,

It follows from the above relation that y takes all real values except 6 when x takes values in the set R – {3}. Therefore, Range (f) = R {6}.

Question 6.
Find the range of the following functions given by f(x) = \(\frac{1}{2-\sin 3 x}\)
Solution:

You can Download Samacheer Kalvi 9th Social Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Social Science History Solutions Chapter 1 Evolution of Humans and Society – Prehistoric Period

Evolution of Humans and Society – Prehistoric Period Textual Exercise

I. Choose the correct answer.

Question 1.
………….. is genetically closest to humans.
(a) Gorilla
(b) Chimpanzee
(c) Orang-utan
(d) Great Apes
Answer:
(b) Chimpanzee

Question 2.
The period called ……………. marks the beginning of agriculture and animal domestication.
(a) Palaeolithic
(b) Mesolithic
(c) Neolithic
(d) Megalithic
Answer:
(c) Neolithic

Question 3.
Direct ancestor of modem man was ……………..
(a) Homo habilis
(b) Homo erectus
(c) Homo sapiens
(d) Neanderthal man
Answer:
(c) Homo sapiens

Question 4.
………….. refers to the area covering Egypt, Israel-Palestine and Iraq.
(a) Great Rift Valley
(b) Fertile Crescent
(c) Solo river
(d) Neander Valley
Answer:
(b) Fertile Crescent

Question 5.
Sir Robert Bruce Foote, a geologist from England first discovered the …………. tools at Pallavaram near Chennai.
(a) Stone Age
(b) Palaeolithic
(c) Mesolithic
(d) Neolithic
Answer:
(b) Palaeolithic

Question 6.
(i) The period before the introduction of writing is called pre-history.
(ii) The pre-historic people developed language, made beautiful paintings and artefacts.
(iii) The pre-historic societies are treated as literate.
(iv) The pre-historic period is called ancient. .
(a) (i) is correct
(b) (i) and (ii) are correct
(c) (i) and (iv) are correct
(d) (ii) and (iii) are correct
Answer:
(c) (i) and (iv) are correct

Question 7.
(i) The Neolithic people used polished stone axes called Celts.
(ii) Evidence of Neolithic village is found at Payyampalli in Chennai district.
(iii) The cultural period that succeeded the Neolithic is called the Bronze Age.
(iv) The period that witnessed domestication .of animals and cultivation of crops is called Mesolithic.
(a) (i) is correct
(b) (ii) is correct
(c) (ii) and (iii) are correct
(d) (iv) is correct
Answer:
(a) (i) is correct

Question 8.
Assertion (A): Many of the Mesolithic sites are found nearby rivers and tanks.
Reason (R): Irrigation management developed during Mesolithic period.
(a) A and R are correct and R explains A
(b) A and R are correct but R doesn’t explain A
(c) A is correct but R is incorrect
(d) A and R both are incorrect
Answer:
(d) A and R both are incorrect

II. Fill in the blanks.

1. The primitive multi-cellular life first appeared in the age of ……………..
2. Hand axes and cleavers are important tool types of …………. culture.
3. The methods and techniques involved in the production of stone tools are called ………………… technology.
4. ………………. is known as the Middle Stone Age, as it is placed between the Palaeolithic and Neolithic.

Answers:

1. Proterozoic
2. Low Palaeolithic
3. Lithic
4. Mesolithic period

III. Find out the correct statement.

Question 1.
(a) The concept ‘survival of the fittest’ contributed to the scientific understanding of human origins.
(b) The book “On the Origin of Species” was published by Herbert Spencer.
(c) Darwin’s theory of biological evolution connects with the process of natural selection.
(d) Geology is the study of lithic technology.
Answer:
(a) correct
(b) incorrect
(c) correct
(d) incorrect

Question 2.
(a) Among the great Apes Orangutan is genetically the closest to humans.
(b) The ancestors of humans were called Hominins and their origins have been traced to Africa.
(c) Flake is a small chip that has flaking on both sides.
(d) Acheulian is the main block of stone from which small1 chips are flaked by using a hammerstone.
Answer:
(a) incorrect
(b) correct
(c) incorrect
(d) incorrect

IV. Match the following.

Answer:
1. (e)
2. (c)
3. (b)
4. (a)
5. (d)

V. Answer the following briefly.

Question 1.
Discuss how the age of speculation made humans become conscious and knowledgeable.
Answer:

1. Humans are the only species on earth concerned with understanding as well as explaining the world and the universe.
2. In the course of evolution, humans became conscious and knowledgeable.
3. They turned curious and began to think and ask questions about nature, organisms and the world around them.
4. They worshipped Sun, Moon and various natural forces about which they developed their own understanding, some of which is not scientific.

Question 2.
Write a note on the impact of pastoralism on the prehistoric people in Tamil Nadu.
Answer:

1. The people in the Age practiced agriculture, domesticated cattle and sheep.
2. Some of the groups were still hunting and gathering.
3. Millets & rice were cultivated.
4. Irrigation management developed in this period. In the deltaic regions irrigation as a technology had developed.
5. Evidences of rice is seen in Megalithic sites like Adidchanallur in Thoothukudi district and Porunthal near Palani.

Question 3.
List out the features of Megalithic Burial types.
Answer:

1. The Iron age is also known as megalithic since people created burials with large stones for the dead people.
2. Within these burials, the skeletons or few bones of the dead persons were placed along with grave goods including iron objects, Camelian beads, and bronze objects.
3. Some of the burials do not have human bones and they have only the grave goods.
4. They may be called memorial burials.

Question 4.
Examine the tool making technical skills of lower Palaeolithic people.
Answer:

1. Hand axes and cleavers are the important tool types of the Lower palaeolithic period.
2. These tools were fitted with a wooden and bone handle. They were used for cutting, piercing and digging.
3. The people also used hammer stones and spheroids.
4. The quartzite pebbles and cobbles were chosen as raw materials.
   The tools are found in the soil deposits and also in the exposed river side.

VI. Answer all the questions given under each caption.

Question 1.
Hominid and Hominins.
(a) Who are Hominids?
Answer:
Hominids refer to all the species of the modem and extinct great apes, which also includes humans.

(b) Who was the earliest human ancestor to make tools in Africa?
Answer:
Homo habilis (handy human) was the earliest known human ancestors to make tools in Africa about 2.6 million years ago.

(c) How are modern humans known?
Answer:
Modem-humans are known as Homo sapiens.

(d) Name any one species of this tribe.
Answer:
Homo erectus – extinct Humans are the only living species.

Question 2.
Earliest Lithic Assemblages of Human ancestors.
(a) Where are Acheulian tools reported to have been found in Karnataka and in Madhya Pradesh?
Answer:
Acheulian tools are reported to have been found in Isampur in Karnataka and Bhimbetka in Madhya Pradesh.

(b) What is meant by Lithic Technology?
Answer:
‘Lith’ means stone. The methods and techniques involved in the production of stone tools are called lithic technology.

(c) What are Biface tools?
Answer:
Bifaces are tools that have to flake on both sides (bi = two, face = side).

(d) Name a few stone tools used by human ancestors.
Answer:
Core is the main block of stone. Flake is a small chip removed from a large stone block. Levalloisian tools include long blades and burins. Burin is a stone-made chisel with a sharp cutting edge.

VII. Answer the following in detail.

Question 1.
The developments in the fields of agriculture, pottery, and metal tools are considered a landmark in the life of the Megalithic period- Substantiate.
Answer:
(a) Agriculture:

1. People practiced agriculture, domesticated cattle, and sheep.
2. Millets and rice were cultivated.
3. Irrigation management developed since many of the megalithic sites are found nearby rivers and tanks.
4. In the deltaic region, irrigation as technology had developed.
5. Evidence of rice is seen in the megalithic sites like Adichanallur in Thoothukudi district and Porunthal near Palani.

(b) Pottery:

1. Pottery is important evidence found in archaeological sites.
2. In the iron age and Sangam age people used black and red colours to make blackware and redware pottery.
3. Potteries were used for cooking, storage, and dining purposes.
4. The black and redware pottery has a black inside and a red outside, with lustrous surfaces.

(c) Metal tools:

1. Weapons such as swords and daggers, axes, chisels, lamps and tripod stands are also found.
2. The iron tools were used for agriculture, hunting and gathering and in battles.

Question 2.
The history of humans is closely related to the history of the earth. Elucidate.
Answer:

• The history of humans is closely related to the history of the earth.
• The earth contains geological, archaeological, and biological records of historical times in its upper layers.
• They are important for reconstructing the history of the earth and various living organisms.
• The fossil bones of the human ancestors are embedded in the earth’s layers.
• Palaeoanthropologists and archaeologists excavate the soil and rock layers on the earth and extract evidence about human ancestors.
• These layers and the fossils are scientifically dated to study the various stages in human evolution and prehistory.
• Through the gathered evidence they attempt to understand the evolution of human history and developments in chronological order.
• The earth was formed approximately 4.54 billion years ago.
• Gradually conditions emerged for the growth of organisms. Then plants and animals came into being and thereby foundation was laid for the evolution of humans. The long span of time in earth’s history is divided into eras, periods, and epochs by the Geologists. Thus the history of humans is closely related to the history of the earth.

Student Activities

Question 1.
Mark the prehistoric sites on the world map.
Answer:
(i) The ancestors of humans were called Hominins and their origins have been traced to Africa.
(ii) You can draw the Prehistoric sites of human ancestors in Africa with the guidance of your teacher.

Question 2.
Assignment with teacher’s guidance.
Answer:
A power-point presentation on the origin of human life.
A power-point presentation on the pre-historic tools.
A power-point presentation on the scripts of the ancient.

Evolution of Humans and Society – Prehistoric Period Additional Questions

I. Choose the correct answer.

1. …………….. is the study of the human past through the analysis and interpretation of material remains.
(a) Geology
(b) Archaeology
(c) History
(d) None of the above
Answer:
(b) Archaeology

Question 2.
The beginning of history writing can be traced to the ancient ……………..
(a) Greeks
(b) Egyptians
(c) Romans
(d) Africans
Answer:
(a) Greeks

Question 3.
The DNA of a Chimpanzee is ……………. identical to that of a human being.
(a) 95%
(b) 96%
(c) 97%
(d) 98%
Answer:
(d) 98%

Question 4.
………….. are stone artifacts of small size.
(a) Microliths
(b) Bifaces
(c) Acheulian
(d) core
Answer:
(a) Microliths

Question 5.
Evidence of Neolithic village is found at …………… in Vellore district.
(a) Gudiam
(b) Athirampakkam
(c) Payyampalli
(d) Salem
Answer:
(c) Payyampalli

Question 6.
The ……………. was a formative period and the foundation for the Sangam Age.
(a) Iron Age
(b) Bronze Age
(c) Stone Age
(d) Age of Information Technology
Answer:
(a) Iron Age

Question 7.
(i) We live in the age of Information Technology.
(ii) The internet has literally put the world at our fingertips.
(iii) The Prehistoric people were the pioneers of literacy.
(iv) Powerful Technology developed all of a sudden.
(a) (i) is correct
(b) (ii) & (iii) are correct
(c) (ii) & (iv) are correct
(d) (i) & (iii) are correct
Answer:
(a) (i) is correct

Question 8.
(i) The chimpanzee is genetically the closest to humans.
(ii) Hominins & their origin have been traced to Asia.
(iii) The Hominins emerged around 6 to 5 million years ago.
(iv) The Great Rift valley in Africa has many sites for the Prehistoric period.
(a) (i) is correct
(b) (ii) & (iii) are correct
(c) (i) & (iv) are correct
(d) (iii) is correct
Answer:
(a) (i) is correct and (c) (i) & (iv) are correct

Question 9.
……………… are tools used for scraping the surfaces.
(a) Lunates
(b) Triangles
(c) Scrapers
(d) Cists
Answer:
(c) Scrapers

Question 10.
…………… are pottery jars and were used for burying the dead.
(a) Urns
(b) Cists
(c) Dolmens
(d) Menheirs
Answer:
(a) Urns

II. Fill in the blanks.

1. Prehistoric people were the pioneers of ……………..
2. ………….. were the apes from which modem humans evolved.
3. A prehistoric animal (or) plant that turns to stone over a period of time …………….
4. The earliest tools made by human ancestors are found in ……………. in Kenya.
5. …………….. people buried the dead people systematically.
6. Rice was probably cultivated in India and China around …………… (or) even earlier.
7. Oxen were used in ………….. civilisation for tilling the land.
8. ……………. discovered the first Palaeolithic tools in India at Pallavaram.
9. …………. people perhaps devised the first pottery.
10. The black and Red colour pottery were used by ……………. and people.

Answers:

1. Creative Knowledge
2. Australopithecines
3. Fossil
4. Lomekwi
5. Neanderthals
6. 7000 BCE
7. Sumerian
8. Sir Robert Bruce Foote
9. Neolithic
10. Iron Age & Sangam Age

III. Match the following

a.

Answer:

1. (d)
2. (e)
3. (a)
4. (b)
5. (c)

b.

Answer:

1. (d)
2. (e)
3. (a)
4. (b)
5. (c)

IV. Answer the following briefly.

Question 1.
Discuss when the earth was formed.
Answer:

1. The earth was formed approximately 4.54 billion years ago.
2. Gradually, conditions emerged for the growth of organisms.
3. Then plants and animals came into being and thereby foundation was laid for the evolution of humans.
4. The long span of time in earth’s history is divided into eras periods and epochs by the geologists.

Question 2.
Who proposed the idea of the Three Age system?
Answer:

1. The idea of the Three Age system proposed by CJ. Thomsen became the basis for understanding early human history.
2. He classified the artifacts in the Danish National Museum, Copenhagen, into Stone Age, Bronze Age, and Iron Age.

Question 3.
The Great Rift valley in Africa has evidence for the Prehistoric period. Discuss.
Answer:

• The Great Rift valley in Africa has many sites that have evidence for the prehistoric period.
• The Great Rift valley is a valley-like formation that runs for about 6,400 km from the Northern part of Syria to Central Mozambique in East Africa.
• This geographical feature is visible even from space, and many prehistoric sites are found in Africa.

Question 4.
Write a short note on “Prehistoric cultures”.
Answer:
While the fossil bones are classified as various species such as Homo habilis, Homo erectus, and Neanderthalensis, based on the lithic tools, cultures are assigned names such as Earliest Lithic, Assemblages, Oldowan Technology, Lower, Middle and Upper Palaeolithic, and Mesolithic cultures.

Question 5.
Why were the Levalloisian tools called so?
Answer:

1. The lithic tool-making tradition of the Levalloisian belonged to this period.
2. Levalloisian tools are the implements made after preparing the core.
3. These tools are found in Europe and Central and Western Asia.
4. The Levalloisian tools are the implements made after preparing the core. It was named after the town of Levallois in France.

Question 6.
What was the main factor for the development of early civilisations?
Answer:

1. As a result of domestication and cultivating plants, there was excess food production.
2. The surplus food production was the main factor for the development of early civilizations.

Question 7.
Describe the burials in the Sangam Age.
Answer:

1. The Sangam literature mentions the various burial practices of the people.
2. The Megalithic burials are classified as dolmens, cists, menheirs, rock-cut caves, um burials, and sarcophagus.
3. The burial types of Kodakkal (umbrella stone), Toppikkal (hot stone), and Paththikal (hood stone) are found in Kerala.

V. Answer all the questions given under each caption.

(A) Oldest Museum.
Question 1.
Name the oldest museum, in the world.
Answer:
The museum of Ennigaldi Nanna in Mesopotamia.

Question 2.
When was it established?
Answer:
It was established in 530 BCE.

Question 3.
Which is the oldest surviving museum at present?
Answer:
The Capitoline museum in Italy is perhaps the oldest surviving museum at present (1471 CE).

Question 4.
Name the oldest university museum in the world.
Answer:
Ashmolean Museum at Oxford University is the oldest University Museum in the world.

(B) Mesolithic culture.
Question 1.
Mention the evidence for the existence of Mesolithic hunt-gatherers.
Answers:
They are found at Chennai, North Arcot, Dharmapuri, Salem, Coimbatore, Ariyalur, Trichi, Pudukottai, Madurai, Sivagangai, Tirunelveli, and Kanyakumari.

Question 2.
What type of artifacts were used by the people of this period?
Answer:
The people of this period used small artifacts made of Chert and Quartz. .

Question 3.
What are the tool types used by them?
Answer:
The tool types are scrapers, lunates, and triangles.

Question 4.
What did they do for their subsistence?
Answer:
These people hunted wild animals and gathered fruits, nuts, and roots for their subsistence.

VI. Answer the following in detail.

Question 1.
Discuss the Neolithic culture in Tamilnadu.
Answer:

• The culture that domesticated animals and cultivated crops is called Neolithic.
• It is known as the New Stone Age. The Neolithic people used polished stone axes called celts.
• Cattle rearing was their main occupation. They lived in small villages with houses made of thatched roof and walls plastered with clay.
• Evidence of Neolithic village is found at Payyampalli in Vellore district and a few sites in the Dharmapuri region.
• Payyampalli is a village in the Vellore district of Tamil Nadu. The earliest evidence for the domestication of animals and the cultivation of plants is found at this site, which was excavated by the Archaeological Survey of India.
• Evidence for pottery making and cultivation of horse gram and green gram has been found in this village.
• These Neolithic sites were part of the Southern Neolithic Culture of India. They are mainly concentrated in the Andhra Pradesh and Karnataka regions.
• The Neolithic people used stone axes fitted on a wooden handle.
• These polished stone axes are worshipped in many village temples of Tamil Nadu even today.

Question 2.
Domestication of Animals and plants. A milestone in Human History. Explain.
Answer:

1. Rice was probably cultivated in India and China around 7000 BCE or even earlier.
2. Wheat and barley were cultivated at Mehrgarh in the northwestern part of the Indian subcontinent (Pakistan) before 6000 BCE.
3. Animal domestication developed as part of symbiotic life.
4. Dogs may have been domesticated first. Friendly animals were gradually domesticated. Sheep and goat were domesticated around 10,000 BCE in Southwest Asia.
5. Oxen were used in Sumerian civilization for tilling the land. Mehrgarh in Pakistan has evidence of sheep, goat, and cattle domestication in the Neolithic period.

You can Download Samacheer Kalvi 9th Social Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Social Science Civics Solutions Chapter 4 Forms of Government

Forms of Government Textual Exercise

I. Fill in the blanks.

1. ……… are the few examples of the unitary form of government.
2. The Parliamentary government is also known as ……..
3. In the parliamentary form of government ….. is the leader of the majority party.

Answers:

1. England, France
2. cabinet government
3. Prime Minister

II. Fill in the blanks.

Question 1.

Country	Name of the Parliament
USA	…………..
Norway	…………..
…………	Folketing

Answer:

Country	Name of the Parliament
USA	Congress
Norway	Storting
Denmark	Folketing

III. Distinguish Between.

Question 1.
Unitary and federal forms of government.
Answer:

Unitary form of government	The federal form of government
Only one Level of Government or Subunits	Two Levels of Government
Mostly Single Citizenship	Dual Citizenship
Sub Units cannot operate independently	Federal Units are answerable to Central Government
No Division of Power	Division of Power
Centralization of Power	Decentralization of Power

Question 2.
Parliamentary and presidential form of government.
Answer:

Parliamentary form of government	Presidential form of government
Majority Party Rules	The President is elected by an electoral college for a fixed tenure of four years.
Collective Responsibility	The President governs with the help of a cabinet or a smaller body called ‘Kitchen Cabinet’.
The leadership of the Prime Minister	The President is both the head of the State and the head of government.

IV. Give a short note on:

Question 1.
Unitary form of government
Answer:

1. A unitary system of government or unitary state is a sovereign state governed as a single entity.
2. The Central government is supreme.
3. The administrative divisions exercise only powers that the central government has delegated to them.
4. England, France, Japan, Sri Lanka are examples of a unitary form of governments.

V. Answer the following.

Question 1.
List out the types of constitution.
Answer:

Question 2.
What are the merits of a federal government?
Answer:
Merits of federal form of government

• Reconciliation of local autonomy with national unity.
• Division of power between centre and states leads to administrative efficiency.
• It gives rise to big states
• Distribution of powers check the despotism of central government.
• More suitable for bigger countries.
• It is good for economic and cultural progress.

Question 3.
Write down the differences between the unitary form of government and the federal form of
government.
Answer:

Unitary form of government	The federal form of government
Only one Level of Government or Subunits	Two Levels of Government
Mostly Single Citizenship	Dual Citizenship
Sub Units cannot operate independently	Federal Units are answerable to Central Government
No Division of Power	Division of Power
Centralisation of Power	Decentralisation of Power

VI. Answer in detail.

Question 1.
Write about the merits of a unitary form of government.
Answer:
Merits of a unitary form of government

1. Suitable for small countries.
2. There is no conflict of authority and responsibility.
3. A unitary government will make prompt decisions and take speedy action.
4. A unitary government is less expensive.
5. Amendments to the constitution are easy.
6. There is unity, uniformity of law, policy, and administration.

Question 2.
Write about the presidential form of government and what is the difference between presidential and parliamentary forms of government.
Answer:
The Presidential Form Of Government is also known as a non-responsible or non-parliamentary or fixed executive system of government, basically built on the principle of separation of power and is prevalent in the USA, Brazil, Russia, and Sri Lanka among others.

The American President is both the head of the State and the head of government. As the head of State, he occupies a ceremonial position. As the head of government, he leads the executive organ of the government.

The President is elected by an electoral college for a fixed tenure of four years. He cannot be removed by the Congress, except by impeachment for a grave unconstitutional act.

The President governs with the help of a cabinet or a smaller body called ‘Kitchen Cabinet’. It is only an advisory body and consists of non-elected departmental secretaries. They are selected and appointed by him, are responsible only to him, and can be removed by him at any time.

The President and his secretaries are not responsible to Congress for their acts. They neither possess membership in the Congress nor attend its sessions.

Differences between presidential and parliamentary forms of government are:

Parliamentary form of government	Presidential form of government
Prime Minister is from the majority party	President is directly elected by the People
Central Legislature is supreme	President is Supreme
Absence of Separation Powers Centralisation	Separation of Powers
Independent branches with Overlapping functions	Independent branches
President – Head of the State	President – Head of the State
Prime Minister – Head of the Government	President – Head of the Government
Collective leadership	Individual Leadership
Collective and Individual Responsibility	President is not accountable to Congress

Forms of Government Additional Questions

I. Fill in the blanks.

1. ……. is the main agency of the state.
2. The three organs in government are …….., ………, and ……….
3. ……… is the oldest form of government in the United Kingdom.
4. An example of Federal form of Government ……..
5. The …… system of government is the one in which the executive is responsible to the legislature for its policies and acts.
6. The …… form of government is prevalent in the U.S.A.
7. The President governs with the help of a cabinet (or) a small body called …… in the Presidential form of government.
8. An unprecedented development forced the ……… to step down and paved the way for Democracy.
9. Gross National Happiness was first mentioned in the constitution of Bhutan, which was enacted on ……
10. …… and …….. are synonyms, both denoting the exercise of authority in an organization, institution (or) state.
Answers:
1. Government
2. legislature, executive, judiciary
3. Monarchy
4. Argentina
5. Parliamentary
6. Presidential
7. Kitchen Cabinet
8. King Gyanendra.
9. 18^th July 2008
10. Government, Governance

II. Fill up.

Country	Name of the Parliament
Israel	……………………..
	Bundestag

Answer:

Country	Name of the Parliament
Israel	Knesset
Germany	Bundestag

III. Distinguish the following:

Question 1.
Monarchy and Democracy
Answer:

Monarchy	Democracy
A form of movement with a Monarch as the head.	The government is headed by elected representatives.
Power is passed through heritage and bloodline.	This principally supports the election.

IV. Answer the following.

Question 1.
What is the meaning of Government?
Answer:
‘Government’ refers to the executive functions of the state. It denotes a body having authority to make and enforce laws applicable to the civil, corporate, religious, academic of other groups.

Question 2.
From where did the term Government was derived?
Answer:
The term Government is derived from Old French ‘governer’, derived from Latin ‘gubernare’ to direct, rule, guide, govern”.

Question 3.
Mention the demerits of Unitary form of Government.
Answer:

• It is not suitable for big countries.
• The central government will have to tackle so many complex problems that lead to administrative delay
• The central government will not concentrate on local problems, local interest and initiative.
• The concentration of powers may pave way for the despotism of the central government.

Question 4.
State the feature of the Parliamentary form of governance.
Answer:
Features of parliamentary form of government

• Nominal and Real Executives
• Majority Party Rule
• Collective Responsibility
• Dual Membership
• The leadership of the Prime Minister

Question 5.
State the merits of the Presidential system of government.
Answer:
Merits of the presidential system of government

• Democratic
• Effective Control by the President
• Facilitate decision-making
• State government

Question 6.
Write down the characteristics of good governance.
Answer:
Characteristics of good governance:

• Participation
• Rule Of Law
• Transparency
• Responsiveness
• Consensus Orientation
• Equity
• Effectiveness And Efficiency
• Accountability

V. Answer in detail.

Question 1.
Explain the Federal form of Government.
Answer:
The classification of governments into unitary and federal is based on the nature of relations between the national and the regional governments.

A federal government is one in which powers are divided between the national government and the regional governments by the Constitution itself and both operate in their respective jurisdictions independently. U.S.A, Switzerland, Australia, Canada, Russia, Brazil, Argentina have federal form of governments. In a federal model, the national government is known as the Federal government or the Central Government or the Union government and the regional government is known as the state government or the provincial government.

Merits of federal form of government

• Reconciliation of local autonomy with national unity
• Division of power between centre and states leads to administrative efficiency
• It gives rise to big states
• Distribution of powers check the despotism of central government
• More suitable for bigger countries
• It is good for economic and cultural progress

De-merits of federal form of government

• Federal government is weaker when compared to the unitary government.
• Federal government is more expensive
• Provincial tendencies are very common
• Lack of uniformity in Administration
• Threat to national unity
• Distribution of powers between centre and states lead to conflicts
• Double Citizenship
• Rigid constitution cannot be mended easily for changing needs
• The state governments sometimes place hindrances in foreign policy.

Federal features of the Indian constitution

• Dual Government
• Written Constitution
• Division of Powers
• Supremacy of the Constitution. The Constitution is the supreme law of the land.
• The laws enacted by the Centre and the states must confirm to its provisions.
• Rigid Constitution
• Independent Judiciary
• Bicameralism

Question 2.
Explain Gross National Happiness.
Answer:
Gross National Happiness is a developing philosophy as well as an ‘index’ which is used to measure the collective happiness in any specific nation. The concept was first mentioned in the constitution of Bhutan, which was enacted on 18 July 2008.

The term ‘Gross National Happiness’ was coined by the fourth king of Bhutan, Jigme Singye Wangchuck, in the 1970s. The GNH’s central tenets are “Sustainable and equitable socio-economic development; environmental conservation; preservation and promotion of culture; and good governance”. GNH is distinguishable by valuing collective happiness as the goal of governance and by emphasising harmony with nature and traditional values.

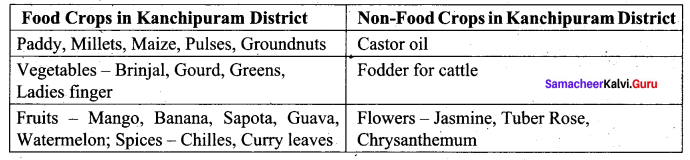
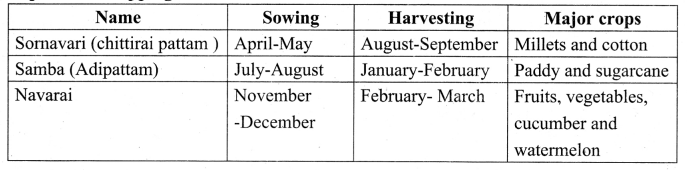
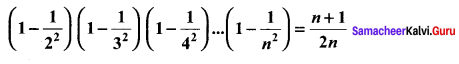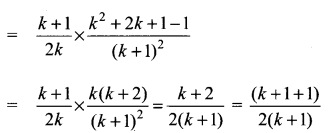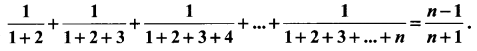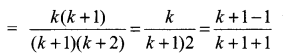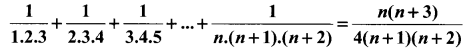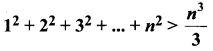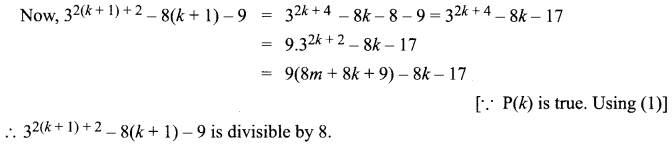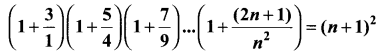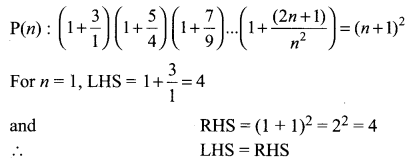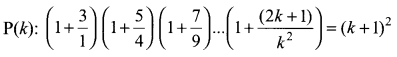You can Download Samacheer Kalvi 10th Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Science Solutions Chapter 5 Acoustics

Samacheer Kalvi 10th Science Acoustics Textual Solved Problems

Question 1.
At what temperature will the velocity of sound in the air be double the velocity of sound in air at 0° C?
Solution:
Let T° C be the required temperature. Let v₁ and v₂ be the velocity of sound at temperatures T₁K and T₂K respectively.
T₁ = 273K (0°C) and T₂ = (T°C + 273)K
\(\frac{v_{2}}{v_{1}}=\sqrt{\frac{\mathrm{T}_{2}}{\mathrm{T}_{1}}}=\sqrt{\frac{273+\mathrm{T}}{273}}=2\)
Here, it is given that, v₂/v₁ = 2
So \(\frac{273+\mathrm{T}}{273}=4\)
T = (273 × 4) – 273 = 819° C.

Question 2.
A source producing a sound of frequency 90 Hz is approaching a stationary listener with a speed equal to (1 / 10) of the speed of sound. What will be the frequency heard by the listener?
Solution:
When the source is moving towards the stationary listener, the expression for apparent frequency is
\(n^{\prime}=\left(\frac{v}{v-v_{s}}\right) n\)
\(\begin{array}{l}{=\left(\frac{v}{v-\left(\frac{1}{10}\right) v}\right) n=\left(\frac{10}{9}\right) n} \\ {=\left(\frac{10}{9}\right) \times 90=100 \mathrm{Hz}}\end{array}\)

Question 3.
A source producing a sound of frequency 500 Hz is moving towards a listener with a velocity of 30 ms^-1. The speed of the sound is 330 ms^-1. What will be the frequency heard by the listener?
Solution:
When the source is moving towards the stationary listener, the expression for apparent frequency is
n’ = \(\left(\frac{v}{v-v_{\mathrm{s}}}\right) n\)
= \(\left(\frac{330}{330-30}\right) \times 500\)
= 550 Hz.

Question 4.
A source of sound is moving with a velocity of 50 ms^-1 towards a stationary listener. The listener measures the frequency of the source as 1000 Hz. what will be the apparent frequency of the source when it is moving away from the listener after crossing him? (velocity of sound in the medium is 330 ms^-1)
Solution:
When the source is moving towards the stationary listener, the expression for apparent frequency is
\(\begin{aligned} n^{\prime} &=\left(\frac{v}{v-v_{\mathrm{s}}}\right) n \\ 1000 &=\left(\frac{330}{330-50}\right) n \\ n &=\left(\frac{1000 \times 280}{330}\right) \end{aligned}\)
n = 848.48 Hz.
The actual frequency of the sound is 848.48 Hz. When the source is moving away from the stationary listener, the expression for apparent frequency is
\(\begin{aligned} n^{\prime} &=\left(\frac{v}{v+v_{\mathrm{s}}}\right) n \\ &=\left(\frac{330}{330+50}\right) \times 848.48 \end{aligned}\)
= 736.84 Hz.

Question 5.
A source and listener are both moving towards each other with a speed v/10 where v is the speed of sound. If the frequency of the note emitted by the source is f, what will be the frequency heard by the listener?
Solution:
When source and listener are both moving towards each other, the apparent frequency is
\(\begin{aligned} n^{\prime} &=\left(\frac{v+v_{l}}{v-v_{s}}\right) n \\ n^{\prime} &=\left(\frac{v+\frac{v}{10}}{v-\frac{v}{10}}\right) n \\ n^{\prime} &=\frac{11}{9} \cdot f \\ &=1.22 f \end{aligned}\)

Question 6.
At what speed should a source of sound move away from a stationary observer so that the observer finds the apparent frequency equal to half of the original frequency?
Solution:
When the source is moving away from the stationary listener, the expression for the apparent frequency is
\(\begin{array}{l}{n^{\prime}=\left(\frac{v}{v+v_{\mathrm{s}}}\right) n} \\ {\frac{n}{2}=\left(\frac{v}{v+v_{\mathrm{s}}}\right) n} \\ {v_{\mathrm{s}}=v}\end{array}\)

Samacheer Kalvi 10th Science Acoustics Textual Evaluation

I. Choose the best Answer

Question 1.
When a sound wave travels through air, the air particles _____.
(a) vibrate along the direction of the wave motion
(b) vibrate but not in any fixed direction
(c) vibrate perpendicular to the direction of the wave motion
(d) do not vibrate.
Answer:
(a) vibrate along the direction of the wave motion

Question 2.
Velocity of sound in a gaseous medium is 330 ms^-1. If the pressure is increased by 4 times without causing a change in the temperature,
the velocity of sound in the gas is:
(a) 330 ms^-1
(b) 660 ms¹
(c) 156 ms^-1
(d) 990 ms^-1
Answer:
(a) 330 ms^-1

Question 3.
The frequency, which is audible to the human ear is _____.
(a) 50 kHz
(b) 20 kHz
(c) 15000 kHz
(d) 10000 kHz.
Answer:
(b) 20 kHz
Hint: Audible frequency hearing the human ear range between 20 Hz to 20 kHz

Question 4.
The velocity of sound in air at a particular temperature is 330 ms^-1. What will be its value when temperature is doubled and the pressure is halved?
(a) 330 ms^-1
(b) 165 ms^-1
(c) 330 × √2 ms^-1
(d) 320 × √2 ms^-1
Answer:
(a) 330 ms^-1

Question 5.
If a sound wave travels with a frequency of 1.25 × 10⁴ Hz at 344 ms^-1, the wavelength will be _____.
(a) 27.52 m
(b) 275.2 m
(c) 0.02752 m
(d) 2.752 m.
Answer:
(c) 0.02752 m
Hint: Velocity of sound = frequency × wavelength
v = nλ
\(\lambda=\frac{v}{n}=\frac{344}{1.24 \times 10^{4}}\)
λ = 0.02752 m.

Question 6.
The sound waves are reflected from an obstacle into the same medium from which they were incident. Which of the following changes?
(a) speed
(b) frequency
(c) wavelength
(d) none of these.
Answer:
(d) none of these.
Hint: If there is the same medium of a reflected obstacle is used, there is no change in speed, frequency and wavelength of the sound.

Question 7.
Velocity of sound in the atmosphere of a planet is 500 ms^-1. The minimum distance between the sources of sound and the obstacle to hear the echo, in point Is is:
(a) 17 m
(b) 20 m
(c) 25 m
(d) 50 m
Answer:
(c) 25 m

II. Fill in the blanks

Question 1.
The rapid back and forth motion of a particle about its mean position is called _____.
Answer:
vibrations.

Question 2.
If the energy in a longitudinal wave travels from south to north, the particles of the medium would be vibrating in _____.
Answer:
both north and south.

Question 3.
A whistle giving out a sound of frequency 450 Hz, approaches a stationary observer at a speed of 33 ms^-1. The frequency heard by the observer is (speed of sound = 330 ms^-1) ______.
Answer:
Data:
v = 330 ms^-1
v_S = 33 ms^-1
n = 450 Hz
n’ =?
Apparent frequency
\(\begin{aligned} n^{\prime} &=\left(\frac{v}{v-v_{\mathrm{S}}}\right) n \\ &=\left(\frac{330}{330-33}\right) \times 450=1.11 \times 450 \end{aligned}\)
n’ = 500 Hz.

Question 4.
A source of sound is travelling with a velocity 40 km/h towards an observer and emits a sound of frequency 2000 Hz. If the velocity of sound is 1220 km/h, then the apparent frequency heard by the observer is _____.
Answer:
2068 Hz
Hint: Apparent frequency heard by the observer.
Data:
v = 1220 km/h (or) 339 ms^-1
v_S = 40 km/h (or) 11.1 ms^-1
n = 2000 Hz
\(\begin{aligned} n^{\prime} &=\left(\frac{v}{v-v_{\mathrm{s}}}\right) n \\ &=\left(\frac{339}{339-11.1}\right) \times 2000 \end{aligned}\)
= 1.03385 × 2000
n’ = 2068 Hz.

III. True or False. If false give the reason

Question 1.
Sound can travel through solids, gases, liquids and even vacuum.
Answer:
False.
Reason: Sound can not travel in a vacuum. This is because sound waves are vibrating waves. In vacuum, where there are no atoms or molecules to vibrate.

Question 2.
Waves created by Earth Quake are Infrasonic.
Answer:
True.

Question 3.
The velocity of sound is independent of temperature.
Answer:
False.
Reason: For an ideal gas the velocity of sound depends on its temperature and is independent of gas pressure.

Question 4.
The velocity of sound is high in gases than liquids.
Answer:
False.
Reason: Velocity of a sound wave is maximum in solids because they are more elastic in nature than liquids and gases. Since gases are least elastic in nature, the velocity of sound is the least in a gaseous medium.
So V_S > V_L > V_G.

IV. Match the following

Question 1.

1. Infrasonic	(a) Compressions
2. Echo	(b) 22 kHz
3. Ultrasonic	(c) 10 Hz
4. High-pressure region	(d) Ultrasonography

Answer:
1. (c) 10 Hz
2. (d) Ultrasonography
3. (b) 22 kHz
4. (a) Compressions

V. Assertion and Reason Type Questions

Mark the correct choice as
(a) If both the assertion and the reason are true and the reason is the correct explanation of the assertion.
(b) If both the assertion and the reason are true but the reason is not the correct explanation of the assertion.
(c) The assertion is true, but the reason is false.
(d) The assertion is false, but the reason is true.

Question 1.
Assertion: The change in air pressure affects the speed of sound.
Reason: The speed of sound in a gas is proportional to the square of the pressure
Answer:
(d) The assertion is false, but the reason is true.

Question 2.
Assertion: Sound travels faster in solids than in gases.
Reason: Solid posses a greater density than that of gases.
Answer:
(b) If both the assertion and the reason are true but the reason is not the correct explanation of the assertion.

VI. Answer very briefly

Question 1.
What is a longitudinal wave?
Answer:
If the particles of the medium vibrate along the direction of propagation of the wave.

Question 2.
What is the audible range of frequency?
Answer:
Audible range of frequency is from 20 Hz to 20000 Hz.

Question 3.
What is the minimum distance needed for an echo?
Answer:

1. The minimum distance required to hear an echo is 1/20th part of the magnitude of the velocity of sound in air.
2. If you consider the velocity of sound as 344 ms^-1, the minimum distance required to hear an echo is 17.2 m.

Question 4.
What will be the frequency sound having 0.20 m as its wavelength, when it travels with a speed of 331 m s^-1?
Answer:
Speed v = 331 m/s
Let the wave length be λ = 0.2 m
Let the frequency be n
∴ Frequency n = \(\frac{v}{λ}\) = \(\frac{331}{0.2}\) = \(\frac{3310}{2}\)
∴ Frequency = 1655 Hz

Question 5.
Name three animals, which can hear ultrasonic vibrations.
Answer:
Mosquitos, bats and dogs are the three animals that can hear ultrasonic vibrations.

VII. Answer briefly

Question 1.
Why does sound travel faster on a rainy day than on a dry day?
Answer:
When humidity increases, the speed of sound increases. That is why you can hear sound from long distances clearly during rainy seasons.

Question 2.
Why does an empty vessel produce more sound than a filled one?
Answer:
In an empty vessel, multiple reflections of sound takes place. Hence more sound is produced in an empty vessel than tilled one.

Question 3.
Air temperature in the Rajasthan desert can reach 46°C. What is the velocity of sound in air at that temperature? (v₀ = 331 ms^-1)
Answer:
Velocity of sound, v₀ = 331 ms^-1
Air temperature, T = 46° C
Velocity of sound in air temperature v_T = (v₀ + 0.61T) ms^-1
= 331 + (0.61 × 46)
= 331 + 28.06
v_T = 359.06 ms^-1.

Question 4.
Explain why the ceilings of concert halls are curved.
Answer:
The ceilings of concert halls are curved so that multiple reflections of sound waves can take place.
The parabolic surfaces are used to focus the sound at a particular point. Hence sound will be louder.

Question 5.
Mention two cases in which there is no Doppler effect in sound?
Answer:

1. When source (S) and listener (L) both are at rest.
2. When S and L move in such a way that distance between them remains constant.
3. When source S and L are moving in mutually perpendicular directions.
4. If the source is situated at the centre of the circle along which the listener is moving.

VIII. Problem Corner

Question 1.
A sound wave has a frequency of 200 Hz and a speed of 400 ms^-1 in a medium. Find the wavelength of the sound wave.
Solution:
A sound wave of frequency, n = 200 Hz
Speed, v = 400 ms^-1
The wavelength of the sound wave, λ = \(\frac{v}{n}\)
λ = \(\frac{400}{200}\) = 2 m.

Question 2.
The thunder of cloud is heard 9.8 seconds later than the flash of lightning. If the speed of sound in air is 330 ms^-1, what will be the height of the cloud?
Answer:
Speed of sound in air v = 330 m/s
Time to hear thunder t = 9.8 s
∴ Height of the cloud = v × t
= 330 × 9.8
= 3234 m.

Question 3.
A person who is sitting at a distance of 400 m from a source of sound is listening to a sound of 600 Hz. Find the time period between successive compressions from the source?
Solution:
Frequency = \(\frac{1}{\text { Time period }}\)
Time period = \(\frac{1}{\text { Frequency }}=\frac{1}{600}\)
T = 0.00167 seconds
The time period between successive compressions from the source is 0.00167 seconds.

Question 4.
An ultrasonic wave is sent from a ship towards the bottom of the sea. It is found that the time interval between the transmission and reception of the wave is 1.6 seconds. What is the depth of the sea, if the velocity of sound in the seawater is 1400 ms^-1?
Solution:

The depth of the sea is 1120 m.

Question 5.
A man is standing between two vertical walls 680 m apart. He claps his hands and hears two distinct echoes after 0.9 seconds and 1.1 seconds respectively. What is the speed of sound in the air?
Solution:
Given data is
d = 680 m
t₁ = 0.9 s
t₂ = 1.1 s
v = ?
\(\text { Velocity }=\frac{\text { Distance travelled by sound }}{\text { Time taken }}\)
\(v=\frac{2 d}{t}\)

Question 6.
Two observers are stationed in two boats 4.5 km apart. A sound signal sent by one, under water, reaches the other after 3 seconds. What is the speed of sound in the water?
Answer:
Distance of boats d = 4.5 × 10³ m
= 4500 m.
Time t = 3 s
Speed of sound in water = \(\frac{d}{t}\)
= \(\frac{4500}{3}\)
= 1500 m/s

Question 7.
A strong sound signal is sent from a ship towards the bottom of the sea. It is received back after 1 s What is the depth of sea given that the speed of sound in water 1450 ms^-1?
Solution:
Velocity of sound in water \(=\frac{\text { Distance travelled by sound }}{\text { Time taken }}\)
Depth of the sea, d = velocity × time
\(d=\frac{v t}{2}=\frac{1450 \times 1}{2}\) = 725 m.

IX. Answer in Detail

Question 1.
What are the factors that affect the speed of sound in gases?
Answer:
In the case of gases, the following factors affect the velocity of sound waves.
Effect of density : The velocity of sound in a gas is inversely proportional to the square root of the density of the gas. Hence, the velocity decreases as the density of the gas increases.
v ∝\(\sqrt{\frac{1}{d}}\)

Effect of temperature : The velocity of sound in a gas is directly proportional to the square root of its temperature. The velocity of sound in a gas increases with the increase in temperature v ∝ √T. Velocity at temperature T is given by the following equation:
V_r = (v_o + 0.61 T)ms^-1.
Here, v_o is the velocity of sound in the gas at 0° C. For air, v_o = 331 ms^-1. Hence, the velocity of sound changes by 0.61 ms^-1 when the temperature changes by one degree Celsius.

Effect of relative humidity : When humidity increases, the speed of sound increases. That is why you can hear sound from long distances clearly during rainy seasons.

Question 2.
What is mean by the reflection of sound? Explain.
Answer:
Reflection of Sound:
The bouncing of sound waves from the interface between two media is termed as the reflection of sound.
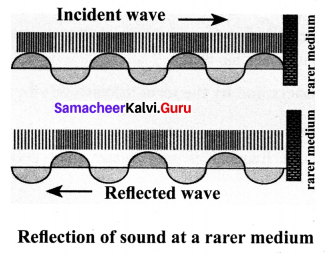
(a) Reflection at the boundary of a rarer medium

• Consider a wave travelling in a solid medium striking on the interface between the solid and the air. The compression exerts a force F on the surface of the rarer medium.
• As a rarer medium has smaller resistance for any deformation, the surface of separation is pushed backwards.
• As the particles of the rarer medium are free to move, a rarefaction is produced at the interface. Thus, compression is reflected as rarefaction and a rarefaction travels from right to left.

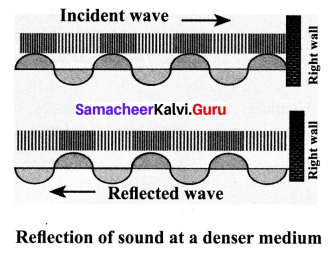
(b) Reflection at the boundary of a denser medium

• A longitudinal wave travels in a medium in the form of compressions and rarefactions. Suppose a compression travelling in the air from left to right reaches a rigid wall.
• The compression exerts a force F on the rigid wall. In turn, the wall exerts an equal and
  opposite reaction R = -F on the air molecules. This results in a compression near the rigid wall.
• Thus, a compression travelling towards the rigid wall is reflected back as a compression. That is the direction of compression is reversed.

(c) Reflection at sound in curved surfaces

• When the sound waves are reflected from the curved surfaces, the intensity of the reflected waves is changed.
• When reflected from a convex surface, the reflected waves are diverged out and the intensity is decreased.
• When sound is reflected from a concave surface, the reflected waves are converged and focused at a point. So the intensity of reflected waves is concentrated at a point.
• Parabolic surfaces are used when it is required to focus the sound at a particular point. Hence, many halls are designed with parabolic reflecting surfaces.
• In elliptical surfaces, sound from one focus will always be reflected the other focus, no matter where it strikes the wall.

Question 3.
(a) What do you understand by the term ‘ultrasonic vibration’?
(b) State three uses of ultrasonic vibrations.
(c) Name three animals which can hear ultrasonic vibrations.
Answer:
(a) Ultrasonic vibrations are the vibration with frequency greater than 20 KHz. Human ear cannot detect the ultrasonic vibration.

(b) (i) Ultrasonic waves are used in ultrasonography.
(ii) It is used to get signal images of a developing embryo in the mother’s uterus.
(in) They are used to forecast about tsunami and earthquake.

(c) Certain creatures like dog, bats, dolphins and mosquito can detect the waves.

Question 4.
What is an echo?
(a) State two conditions necessary for hearing an echo.
(b) What are the medical applications of echo?
(c) How can you calculate the speed of sound using echo?
Answer:
Echo: An echo is the sound reproduced due to the reflection of the original sound from various rigid surfaces such as walls, ceilings, surfaces of mountains, etc.

(a) (i) The persistence of hearing for human ears is 0.1 second. This means that we can hear two sound waves clearly if the time interval between the two sounds is at least 0.1 s. Thus, the minimum time gap between the original sound and an echo must be 0.1 s.

(ii) The above criterion can be satisfied only when the distance between the source of the sound and the reflecting surface would satisfy the following equation:
\(\begin{aligned} \text { Velocity } &=\frac{\text { Distance travelled by sound }}{\text { Timetaken }} \\ v &=\frac{2 d}{t} \\ d &=\frac{v t}{2} \end{aligned}\)
Since, t = 0.1 second, then \(d=\frac{v \times 0.1}{2}=\frac{v}{20}\)

(b) (i) The principle of echo is used in obstetric ultrasonography, which is used to create real – time visual images of the developing embryo or fetus in the mother’s uterus.
(ii) This is a safe testing tool, as it does not use any harmful radiations.

(c) Apparatus required:
A source of sound pulses, a measuring tape, a sound receiver and a stopwatch.
Calculation of speed of sound:
The sound pulse emitted by the source travels a total distance of 2nd while travelling from the source to the wall and then back to the receiver.
The time taken for this has been observed to be ‘t’. Hence, the speed of the sound wave is given by:
\(\text { Speed of sound }=\frac{\text { Distance travelled }}{\text { Timetaken }}=\frac{2 d}{t}\).

X. HOT Questions

Question 1.
Suppose that a sound wave and a light wave have the same frequency, then which one has a longer wavelength?
(a) Sound
(b) Light
(c) both (a) and (b)
(d) data not sufficient.
Answer:
(b) light
Explanation: The light wave has a longer wavelength because it has much greater speed.

Question 2.
When sound is reflected from a distant object, an echo is produced. Let the distance between the reflecting surface and the source of sound remain the same. Do you hear an echo sound on a hotter day? Justify your answer.
Answer:
Echo of sound is heard with less velocity and intensity on a hotter day. Because the velocity of sound is directly proportional to temperature of air. On a hotter day temperature will be higher so velocity of sound will be changed by higher values.

Samacheer Kalvi 10th Science Acoustics Additional Questions

I. Choose the best answer

Question 1.
Light can travel in a vacuum but not sound because of ______.
(a) speed of sound is very slow than light.
(b) light waves are electromagnetic in nature.
(c) sound waves are electromagnetic in nature.
(d) light waves are not electromagnetic in nature.
Answer:
(a) speed of sound is very slow than light.
Hint: Light can travel in a vacuum because light waves are electromagnetic in nature.

Question 2.
In a longitudinal wave there is a state of maximum compression at a point at an instant. The frequency of wave is 50 Hz. After what time will the same point be in the state of maximum rarefaction:
(a) 50 s
(b) 25 s
(c) 0.01 s
(d) 0.002 s
Answer:
(c) 0.01 s

Question 3.
When sound travels from air to water, which parameter does not change?
(a) Wavelength
(b) Frequency
(c) Velocity
(d) Temperature.
Answer:
(b) Frequency
Hint: Frequency remains unchanged when sound travels from air to water.

Question 4.
When a wave passes from one medium to another, there is a change of:
(a) Wavelength and velocity
(b) Wavelength and frequency
(c) Velocity and frequency
(d) Velocity only
Answer:
(a) Wavelength and velocity

Question 5.
At what temperature, the speed of sound in the air will become double of its value at 27°C?
(a) 54° C
(b) 627° C
(c) 327° C
(d) 927° C.
Answer:
(d) 927° C.
Hint:
\(\frac{v_{1}}{v_{2}}=\sqrt{\frac{\mathrm{T}_{1}}{\mathrm{T}_{2}}} \Rightarrow \frac{v_{1}}{2 v_{1}}=\sqrt{\frac{\mathrm{T}_{1}}{\mathrm{T}_{2}}}\)
⇒ \(\frac{1}{4}=\frac{27+273}{\mathrm{T}_{2}}\)
⇒ T₂ = 300 × 4 = 1200 K
⇒ T₂ = 1200 – 273 = 927° C.

Question 6.
Sound waves from a point source are propagating in all directions. What will be the ratios of amplitude at a distance 9 m and 25 m from the source?
(a) 9 : 25
(b) 25 : 9
(c) 3 : 5
(d) 81 : 625
Answer:
(b) 25 : 9

II. Fill in the blanks:

Question 1.
Sound waves in a gas are ______.
Answer:
Longitudinal.

Question 2.
The velocity of sound is the largest in ______.
Answer:
Steel.

Question 3.
Hertz is the unit of ______.
Answer:
Frequency.

Question 4.
Sound travels in rocks in the form of ______.
Answer:
Both longitudinal and transverse elastic waves.

Question 5.
The velocity of sound varies directly as the square root of the ______.
Answer:
The absolute temperature of the gas.

Question 6.
Reflection of sound waves obey the ______.
Answer:
Laws of reflection.

Question 7.
RADAR is the short form of ______.
Answer:
Radio Detection and Ranging.

Question 8.
The abbreviation of SONAR is ______.
Answer:
Sound Navigation and Ranging.

III. Match the following

Question 1.

Medium	Speed of Sound (m/s)
(i) Copper	(a) 343
(ii) Water	(b) 331
(iii) Air (0° c)	(c) 5010
(iv) Air (at 20° c)	(d) 1493

Answer:
(i) (c) 5010
(ii) (d) 1493
(iii) (b) 331
(iv) (a) 343.

Question 2.

Waves	Range
(i) Audible	(a) 340 m/s
(ii) Sound	(b) greater than 20kHz
(iii) Infrasonic	(c) 20Hz – 20 kHz
(iv) Light	(d) below 20 Hz
(v) Ultrasonic	(e) 3 × 108 m/s

Answer:
(i) (c) 20 Hz – 20 kHz
(ii) (a) 340 m/s
(iii) (d) below 20 Hz
(iv) (e) 3 × 10⁸ m/s
(v) (b) greater than 20 kHz.

IV. Assertion and Reason Questions

Question 1.
Assertion: Sound wave cannot propagate through a vacuum but light can.
Reason: Sound wave cannot be polarised but light can.
(a) Both assertion and reason are true and the reason is the correct explanation of the assertion.
(b) Both assertion and reason are true but the reason is not the correct explanation of the assertion.
(c) Assertion is true but the reason is false.
(d) Both assertion and reason are false.
Answer:
(b) Both assertion and reason are true but the reason is not the correct explanation of the assertion.
Explanation: Sound waves, being mechanical waves, cannot travel through a vacuum. Light waves, electromagnetic waves, can travel through a vacuum.

Question 2.
Assertion: The velocity of sound increases with increase in humidity.
Reason: Velocity of sound does not depend upon the medium.
(a) both assertion and reason are true and the reason is the correct explanation of the assertion.
(b) both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) Assertion is true but reason is false.
(d) Assertion is false but the reason is true.
Answer:
(c) The assertion is true but the reason is false.
Explanation: Velocity of sound increases with increase in humidity. The velocity of sound depends upon medium.

V. Answer Very Briefly

Question 1.
What is sound? Is it a force or energy?
Answer:
Sound is a vibration that typically propagates as an audible wave of pressure, through a transmission medium such as a gas, liquid or solid. Sound is not a force, it is an energy.

Question 2.
In which type of media, can longitudinal waves be propagated?
Answer:
Longitudinal waves can be propagated through solids, liquids and gases.

Question 3.
How does sound reach our ears from various sources?
Answer:
Sound reaches our ears in the form of transverse waves or vibrations from its source of production.

Question 4.
What is the minimum distance between two points in a wave having a phase difference of 2π?
Answer:
The minimum distance is the wavelength.

Question 5.
Suppose you and your friend are on the Moon. Will you be able to hear any sound produced by your friend?
Answer:

• As the Moon does not have air, you will not be able to hear any sound produced by your friend.
• Hence, you understand that the sound produced due to the vibration of different bodies needs a material medium like air, water, steel, etc, for its propagation.
• Hence, sound can propagate through a gaseous medium or a liquid medium or a solid medium.

Question 6.
What is the effect of pressure on the speed of sound in gas?
Answer:
The increase of pressure has no effect on the speed of sound in a gas.

Question 7.
Write down the difference between the sound and light waves.
Answer:

Sound	Light
1. Medium is required for the propagation	1. Medium is not required for the propagation.
2. Sound waves are longitudinal.	2. Light waves are transverse.
3. Wavelength ranges from 1.65 cm to 1.65 m.	3. Wavelength ranges from 4 × 10-7 m to 7 × 10-7 m.
4. Sound waves travel in the air with a speed of about 340 ms-1 at NTP.	4. Light waves travel in the air with a speed of 3 × 108 ms-1

Question 8.
Define particle velocity.
Answer:
The velocity with which the particles of the medium vibrate in order to transfer the energy in the form of a wave is called particle velocity.

Question 9.
Define wave velocity.
Answer:
The velocity with which the wave travels through the medium is called wave velocity.

Question 10.
Define velocity of a sound wave.
Answer:
The distance travelled by a sound wave in unit time is called the velocity of a sound wave.
\(\text { Velocity }=\frac{\text { Distance }}{\text { Time taken }}\)

Question 11.
State the laws of reflection of sound.
Answer:
The incident wave, the normal to the reflecting surface and the reflected wave at the point of incidence lie in the same plane.
The angle of incidence ∠i is equal to the angle of reflection ∠r.

Question 12.
State ‘Laws of reflection’.
Answer:

• The incident wave, the normal to the reflecting surface and the reflected wave at the point of incidence lie in the same plane.
• The angle of incidence ∠i is equal to the angle of reflection ∠r.

Question 13.
What is meant by rarer and denser medium?
Answer:

1. Rarer medium: The medium in which the velocity of sound increases compared to other medium is called rarer medium. (Water is rarer compared to air for sound).
2. Denser medium: The medium in which the velocity of sound decreases compared to other medium is called denser medium. (Air is denser compared to water for sound)

VI. Problem Corner

Question 1.
A wave of length 0.60 cm is produced in air and travels with a velocity of 340 ms^-1. Will it be audible to the human ear?
Solution:
Wavelength, λ = 0.6 × 10^-2 m
Velocity of sound, v = 340 ms^-1
Frequency, n = \(\frac{v}{\lambda}\)
⇒ n = \(\frac{340}{0.6 \times 10^{-2}}\)
⇒ n = 566.66 × 10²
⇒ n = 567 × 10² Hz.

Question 2.
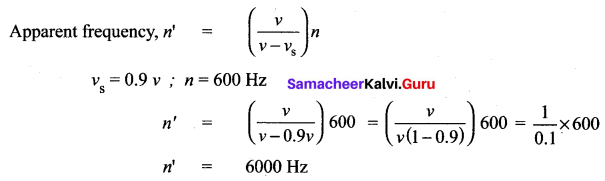
Consider a source moving towards a listener at a speed of 0.9 v. Where v is the velocity of sound. Calculate the apparent frequency if the actual frequency is 600 Hz.
Solution:

Question 3.
Audible frequencies have a range of 20 Hz to 20,000 Hz. Express it in terms of wavelength in air.
Answer:
Let the velocity of sound in air be 340 m/s
Initial frequency v₁ = 20 Hz
Initial wavelength λ₁ = \(\frac{v}{V_1}\)
= \(\frac{340}{20}\) = 17 m
Final frequency v₂ = 20 × 10³ Hz
Final wavelength λ₂ = \(\frac{340}{20×10³}\)
= 17 × 10^-3 = 0.017 m
The range of wavelength is from 17 m to 0.017 m

VII. Answer in detail.

Question 1.
Write down the applications of echo?
Answer:
Applications of echo:

• Some animals communicate with each other over long distances and also locate objects by sending the sound signals and receiving the echo as reflected from the targets.
• The principle of echo is used in obstetric ultrasonography, which is used to create real – time visual images of the developing embryo or fetus in the mother’s uterus. This is a safe testing tool, as it does not use any harmful radiations.
• Echo is used to determine the velocity of sound waves in any medium.

Question 2.
Classify sound waves based on their frequencies.
Answer:
(i) Audible waves : These are sound waves with a frequency ranging between 20 Hz and 20,000 Hz. These are generated by vibrating bodies such as vocal cords, stretched strings etc.

(ii) Infrasonic waves : These are sound waves with a frequency below 20 Hz that cannot be heard by the human ear. eg: waves produced during earth quake, ocean waves, sound produced by whales, etc.

(iii) Ultrasonic waves : These are sound waves with a frequency greater than 20 kHz, Human ear cannot detect these waves, but certain creatures like mosquito, dogs, bats, dolphins can detect these waves, eg: waves produced by bats.

Question 3.
Write down the concept of Ear trumpet and Megaphone.
Answer:
Ear trumpet:

• Ear trumpet is a hearing aid, which is useful by people who have difficulty in hearing.
• In this device, one end is wide and the other end is narrow. The sound from the sources fall into the wide end and are reflected by its walls into the narrow part of the device. This helps in concentrating the sound and the sound enters the eardrum with more intensity. This enables a person to hear the sound better.

Megaphone:

• A megaphone is a horn – shaped device used to address a small gathering of people.
• It’s one end is wide and the other end is narrow. When a person speaks at the narrow end, the sound of his speech is concentrated by the multiple reflections from the walls of the tube. Thus, his voice can be heard loudly over a long distance.

Question 4.
What is the Doppler effect? Derive the formula for the change in apparent frequency
1. Both source and listener move towards and away from each other.
2. Both source and listener move one behind the other source follows the listener and listener follows the source.
3. A source at rest, listener moves towards and away from the source.
4. A listener at rest, the source moves towards and away from the listener.
Answer:
1.

Position of source and listener	Note	Expression for apparent frequency
(i) Both source and listener move (ii) They move towards each other	(a) Distance between source and listener decreases. (b) Apparent frequency is more than actual frequency.	\(n^{\prime}=\left(\frac{v+v_{\mathrm{L}}}{v-v_{\mathrm{S}}}\right) n\)
(i) Both source and listener move (ii) They move away from each other	(a) Distance between source and listener increases. (b) Apparent frequency is less than actual frequency. (c) vS and vL become opposite to that in case-1.	\(n^{\prime}=\left(\frac{v-v_{\mathrm{L}}}{v+v_{\mathrm{S}}}\right) n\)

2.

Position of source and listener	Note	Expression for apparent frequency
(i) Both source and listener move (ii) They move one behind the other (iii) Source follows the listener	(a) Apparent frequency depends on the velocities of the source and the listener. (b) vS becomes opposite to that in case-2.	\(n^{\prime}=\left(\frac{v-v_{\mathrm{L}}}{v-v_{\mathrm{S}}}\right) n\)
(i) Both source and listener move (ii) They move one behind the other (iii) The listener follows the source	(a) Apparent frequency depends on the velocities of the source and the listener. (b) vS and vL become opposite to that in case-3.	\(n^{\prime}=\left(\frac{v+v_{\mathrm{L}}}{v+v_{\mathrm{s}}}\right) n\)

3.

Position of source and listener	Note	Expression for apparent frequency
(i) Source at rest (ii) Listener moves towards the source	(a) Distance between source and listener decreases. (b) Apparent frequency is more than actual frequency. (c) vS = 0 in case-1.	\(n^{\prime}=\left(\frac{v+v_{\mathrm{L}}}{v}\right) n\)
(i) Source at rest (ii) Listener moves away from the source	(a) Distance between source and listener increases. (b) Apparent frequency is less than actual frequency. (c) vS = 0 in case-2.	\(n^{\prime}=\left(\frac{v-v_{\mathrm{L}}}{v}\right) n\)

4.

Position of source and listener	Note	Expression for apparent frequency
(i) Listener at rest (ii) Source moves towards the listener	(a) Distance between source and listener decreases. (b) Apparent frequency is more than actual frequency. (c) vL = 0 in case-1.	\(n^{\prime}=\left(\frac{v}{v-v_{\mathrm{S}}}\right) n\)
(i) Listener at rest (ii) Source moves away from the listener	(a) Distance between source and listener increases. (b) Apparent frequency is less than actual frequency. (c) vL = 0 in case-2.	\(n^{\prime}=\left(\frac{v}{v+v_{\mathrm{S}}}\right) n\)

Question 5.
Explain echo method to measure velocity’ of sound.
Answer:
Apparatus required: A source of sound pulses, a measuring tape, a sound receiver, and a stop watch.
Procedure:

1. Measure the distance ‘d’ between the source of sound pulse and the reflecting surface using the measuring tape.
2. The receiver is also placed adjacent to the source. A sound pulse is emitted by the source.
3. The stopwatch is used to note the time interval between the instant at which the sound pulse is sent and the instant at which the echo is received by the receiver. Note the time interval as ‘t’.
4. Repeat the experiment for three or four times. The average time taken for the given number of pulses is calculated.

Calculation of speed of sound : The sound pulse emitted by the source travels a total distance of 2d while travelling from the source to the wall and then back to the receiver. The time taken for this has been observed to be ‘t’. Hence, the speed of sound wave is given by:
Speed of sound = \(\frac{distence Travelled}{Time Taken}\)
= \(\frac{2d}{t}\)

You can Download Samacheer Kalvi 9th Social Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Samacheer Kalvi 9th Social Science Economics Solutions Chapter 4 Tamilnadu Agriculture

Tamilnadu Agriculture Textual Exercise

I. Choose the correct answer:

Question 1.
Irrigated land surface out of cultivable land is
(a) 27%
(b) 57%
(c) 28%
(d) 49%
Answer:
(b) 57%

Question 2.
Out of the following which is not a food crop?
(a) Bajra
(b) Ragi
(c) Maize
(d) Coconut
Answer:
(d) Coconut

Question 3.
The productivity of paddy during the year 2014-2015
(a) 3,039 kg
(b) 4,429 kg
(c) 2,775 kg
(d) 3,519 kg
Answer:
(b) 4429 kilogram

Question 4.
Both agricultural productivity and food productivity has ……..
(a) decreased
(b) not stable
(c) remained stable
(d) increased
Answer:
(d) Increased

Question 5.
The North-East monsoon period in Tamilnadu ………
(a) August – October
(b) September – November
(c) October – December
(d) November – January
Answer:
(c) October – December

II. Fill in the blanks.

1. The major occupation of people in Tamilnadu is ……..
2. Tamilnadu receives rainfall from the ……. monsoon.
3. The total geographical area of Tamil Nadu is …….. hectares.

Answers:

1. Agriculture
2. Northeast
3. 30 lakh and 33 thousand

III. Match the following:

Answers:
1. (e)
2. (d)
3. (c)
4. (b)
5. (a)

IV. Give short Answers

Question 1.
Give two examples for each food crop and non-food crops.
Answer:

1. Food crops: Paddy, Wheat.
2. Non-food crops: Coconut, Cotton.

Question 2.
What are the factors responsible for the changes in the cropping area?
Answer:
The size of the total cropping land in Tamil Nadu is 4,544 thousand hectares and this keeps on changing every year. Sufficient rains at the proper period will increase this extent of land. Failure or shortage in rainfall leads to the reduction of land usage for cultivation. .

Question 3.
Who monitors the quantity and quality of groundwater?
Answer:
The Union Water Board is constantly monitoring the level and nature of groundwater.

Question 4.
Tabulate the productivity of paddy from 1965 to 2015.
Answer:

Question 5.
On what factors does crop cultivation depend? List out the factors on which crop cultivation depends.
Answer:
Crop cultivation depends on – rainfall, availability of water, weather and market prices.

Question 6.
Differentiate small and marginal farmers.
Answer:

Small Farmers	Marginal Farmers
Small farmers cultivate in lands ranging from 1 -2 hectares.	Marginal farmers cultivate in lands within 1 hectare.

V. Answer in Detail

Question 1.
Give a note on water resources in Tamilnadu.
Answer:

1. There are no perennial rivers in Tamil Nadu.
2. Tamil Nadu receives the required water from the northeast and southwest monsoons.
3. When the southwest monsoon rains are high in the catchment areas of Kavery River in Karnataka, Dams there get filled and in turn, Kavery River in Tamil Nadu gets water.
4. The area under irrigation is about 57% of the total area under cultivation.
5. Canals, lakes, open wells and bore wells also provide water for irrigation.
6. But agriculture in Tamil Nadu is dependent on groundwater.

Question 2.
What are the problems faced by using groundwater for agriculture?
Answer:
Agriculture in Tamil Nadu is dependent mostly on groundwater. Use of groundwater for agriculture creates many hardships too. There would be no suffering if the amount of water taken from the underground and the amount of water that goes into the underground during the rainy season are equal. On the contrary, as the amount of water taken increases, the ground water goes down resulting in complete dryness or change into unusable water.

Question 3.
Discuss the source of irrigation for agriculture.
Answer:

1. The northeast monsoon (oct-Dec) is a major source of water for Tamil Nadu.
2. The Northeast monsoon rains are stored in reservoirs, lakes, and tarns for cultivation.
3. Conventional water bodies like lakes, ponds, and canals provide water for agriculture in Tamil Nadu.
4. 2239 canals mn through Tamil Nadu covering a length of 9750 km.
5. There are 7985 small lakes, 33,142 large lakes, 15 lakh open wells.
6. There are 3,54,000 borewells in the state where agriculture is carried out with the help of these water resources.
7. The area of land that is irrigated from the lakes is very low. Nearly 3.68 lakh hectares of land obtain water from lakes.
8. The canals provide water to 6.68 lakh hectares.
9. Borewells irrigate 4.93 lakh hectares and open wells provide water to 11.91 lakh hectares of land.
10. Still in Tamil Nadu agriculture is dependent on groundwater.

Question 4.
Tabulate the crops grown in Tamil Nadu.
Answer:
Crops grown in Tamil Nadu are:

1. Paddy
2. Black gram
3. Maize
4. Coconut
5. Corn
6. Sugarcane
7. Millets

VI Activity

Question 1.
Analyse the cultivation of food crops and non-food crops of your village/area.
Answer:

Question 2.
Thanjavur is famous for which crop? Why is it so? Research.
Answer:
(a) The Principal crops in Thanjavur District are paddy, green gram, black gram, sugarcane,
cotton, groundnut, gingelly, coconut, fruits and vegetables in the areas where irrigation facility is available.
In the rainfed area cholam, kumbu, ragi, maize, some edible oil seeds, non-edible oilseeds, fodder crops etc.
(b) The land is ideal for growing crops like Rice. The major portion of Thanjavur land consists of alluvial deposits. Thanjavur is known as the Rice bowl of Tamil Nadu.
(c) Soil and Water Management Research Institute Kalluthottam was established in 1972. They conduct research on the improved methods of water conveyance, application, and utilization on rice and other crops grown in the Cauvery Delta zone.

Question 3.
Collect statistical data, where paddy is being cultivated at Thanjavur District, which is called the Nerkalanjium of Tamil Nadu.
Answer:
(a) Thanjavur is known as the Rice bowl of Tamil Nadu.
(b) Samba cultivation has picked up in Thanjavur District.
(c) In Tiruvarur district direct sowing has been done on 70,000 hectares of land, while transplantation has been completed on 11,500 hectares.
(d) High concentrations of rice production is found in the taluks of Orathanadu, Thiruvaiyaru, Kumbakonam, Pabanasam, Thiruvidaimarudur, etc.

Tamilnadu Agriculture Additional Questions

I. Choose the correct answer.

Question 1.
This is the total employee population engaged in agriculture according to the 2001 census.
(a) 48.3%
(b) 49.3%
(c) 47.3%
(d) 46.3%
Answer:
(b) 49.3%

Question 2.
The total geographical area of Tamil Nadu is
(a) one crore thirty lakh and thirty-three thousand hectares
(b) one crore twenty lakh and thirty-two thousand hectares
(c) one crore forty lakh and thirty-three thousand hectares
(d) one crore twenty-five lakh and thirty thousand hectares
Answer:
(a) one crore thirty lakh and thirty-three thousand hectares

Question 3.
The number of blocks identified as excessive users of groundwater are
(a) 140
(b) 141
(c) 139
(d) 138
Answer:
(c) 139

Question 4.
……… cultivation is carried out at a large scale of 30 percent cultivated land area.
(a) Paddy
(b) Varagu
(c) Cholam
(d) Kambu
Answer:
(a) Paddy

Question 5.
Production capacity of rice in Tamil Nadu was …….. Kg per hectare in 2014 – 2015.
(a) 4420
(b) 4422
(c) 4425
(d) 4427
Answer:
(d) 4427

II. Fill in the blanks.

1. The agricultural workers in Tamil Nadu in 2011 were ……..
2. A major portion of the workers involved in agricultural activities are ……… labourers.
3. Most of the cultivators in Tamil Nadu are …….. farmers.
4. There are no …….. rivers in Tamil Nadu.
5. The ……… Board is constantly monitoring the level and nature of groundwater.
6. Tamil Nadu agriculture is dependent on ……….
7. Crops are divided into ……. and ……….

Answers:

1. 96 lakhs
2. landless
3. marginal
4. Perennial
5. Union Ground Water
6. groundwater
7. food, non-food

III. Match the following:

Answers:
1. (d)
2. (a)
3. (b)
4. (c)

IV. Give Short Answers.

Question 1.
What happened to the number of workers engaged in Agriculture in the past ten years?
Answer:
It has been noticed that the number of farmers in Tamilnadu has got reduced during the last 10 years according to the 2011 census data. Similarly, the number of agricultural workers also reduced during the same period.

Question 2.
What type of employees are involved in agricultural activities?
Answer:
A major portion of the workers involved in agricultural activities are landless labourers. All the landholders do not have the same amount of land. Many have very little land and very few people hold large areas of land.

Question 3.
“The total area of land under agriculture is shrinking fast.” What does it show?
Answer:
The total land area under agriculture is shrinking fast not only in Tamilnadu but also throughout India. The number of marginal farmers has increased in India. In contrast, the number of marginal farmers is decreasing in Tamil Nadu. This shows that the farmers are doing other occupations.

Question 4.
Comment on water resources of Tamil Nadu.
Answer:
There are no perennial rivers in Tamil Nadu. Tamil Nadu receives the required water from the Northeast and Southwest monsoons. When the southwest monsoon rains are high in the catchment areas of the Cauvery River in Karnataka dams get filled and in turn, the Cauvery river in Tamil Nadu gets water.

Question 5.
How is the productivity of crops?
Answer:
The productivity of crops continues to increase. For example, the productivity of paddy in 1965 – 66 was 1,409 kg. It increased to 2,029 kg in 1975-76 and 2,372 kg in 1985-86. It . increased to 2,712 kg after a decade. The production was 4,429 kg in the year 2014-15. In the past fifty years, the productivity of paddy has increased more than three times.

V. Answer in Detail.

Question 1.
Explain irrigation and crop types.
Answer:
All cultivated crops can be classified as food crops and non-food crops. 57 percentage of the total land under food grain cultivation is irrigated. In 2014-15, 59 percentage of food crops and 50 percentage of nonfood crops were irrigated in Tamilnadu.

The total area of land cultivated in Tamil Nadu was 59 lakh and 94 thousand hectares in 2014—2015. Out of this non-food crops were 76%.

Paddy cultivation is carried out at a large scale of 30 percent cultivated land area and other food crops in 12 percent area. Millets are cultivated in a very low percentage of area. Sorghum(Cholam) cultivation in 7 percent land area, cumbu in one percent and ragi in 1.7 percent. Other millets occupy 6 percent in the year 2014-2015.

The area cultivatable land changes every year as a result of many factors such as rainfall, availability of water, weather and market prices.

You can Download Samacheer Kalvi 10th Social Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Social Science Geography Solutions Chapter 7 Human Geography of Tamil Nadu

Human Geography of Tamil Nadu Textual Exercise

I. Choose the correct answer.

Question 1.
The delta which is known as Granary of South India is ……………….
(a) Cauvery delta
(b) Mahanadi delta
(c) Godavari delta
(d) Krishna delta
Answer:
(a) Cauvery delta

Question 2.
Second staple food of the people of Tamil Nadu is:
(a) Pulses
(b) Millets
(c) Oilseeds
(d) Rice
Answer:
(b) Millets

Question 3.
Literacy rate of Tamil Nadu as per 2011 census is ……………
(a) 80.32%
(b) 62.33%
(c) 73.45%
(d) 80.33%
Answer:
(d) 80.33%

Question 4.
A major hydro-electric power project of Tamil Nadu is:
(a) Mettur
(b) Papanasam
(c) Sathanur
(d) Tungabhadra
Answer:
(a) Mettur

Question 5.
Number of major and minor ports in Tamil Nadu are
(a) 3 and 15
(b) 4 and 15
(c) 3 and 16
(d) 4 and 16
Answer:
(a) 3 and 15

II. Fill in the blanks.

1. Agriculture of Tamil Nadu constitutes …………….. % of its economy.
2. Sathanur dam is constructed across the river …………..
3. Tamil Nadu ranks …………….. in India with a share of over 20% in total road projects under operation in the Public – Private Partnership (PPP).
4. ………….. is the third largest airport in India after Mumbai and Delhi.
5. The difference between the value of exports and imports is called ………….
Answers:
1. 21
2. Thenpennai
3. Second
4. Chennai International Airport
5. Balance of trade

III. Match the following.

Answer:
1. (b)
2. (d)
3. (a)
4. (c)

IV. Questions 1-2 are assertion and reasoning type

Question 1.
Assertion (A): Coimbatore, Tiruppur and Erode region is called as The Textile Valley of Tamil Nadu.
Reasoning (R): They contribute a major share to the state’s economy through textiles.
(a) Both (A) and (R) are true and (R) explains (A)
(b) Both (A) and (R) are true but, (R) does not explain (A)
(c) (A) is true but (R) is false
(d) (A) is false but (R) is true
Answer:
(a) Both (A) and (R) are true and (R) explains (A)

Question 2.
Assertion (A): The Nilgiris is the least populated district of Tamil Nadu
Reasoning (R): It is located in the western most part of Tamil Nadu.
(а) Both (A) and (R) are true and (R) explains (A)
(b) Both (A) and (R) are true but, (R) does not explain (A)
(c) (A) is true but (R) is false
(d) (A) is false but (R) is false
Answer:
(b) Both (A) and (R) are true but, (R) does not explain (A)

V. Answer the following in briefly.

Question 1.
Explain the cropping seasons of Tamil Nadu.
Answer:

Question 2.
Why is Coimbatore called the Manchester of Tamil Nadu?
Answer:
Coimbatore has the ideal conditions for cotton cultivation – Humid weather in the early stages and hot weather during the harvest period. Cotton cultivation and the textile industries are the reasons to call Coimbatore as the “Manchester of Tamil Nadu”.

Question 3.
Name the important multipurpose projects of Tamil Nadu.
Answer:
Mettur Dam, Amaravathi Dam, Papanasam Dam, Bhavani Sagar Dam.

Question 4.
What is MRTS?
Answer:

1. Mass Rapid Transport System (MRTS) a well established suburban railway network. Currently developing a Metro system, with its first underground operation since May 2017.
2. It is mainly started to manage the crowd during peak hours. The elevated metro system. Connects the heart of the city from North to South.

Question 5.
List out the air ports and sea ports of Tamil Nadu.
Answer:
Airports:

1. Chennai International Airport
2. Coimbatore International Airport
3. Madurai International Airport
4. Tiruchirapalli International Airport

Domestic Airports:

1. Tuticorin and Salem

Sea Port: Major Sea Ports are:

1. Chennai
2. Ennore and
3. Tuticorin
   Intermediate port at Nagapattinam and 15 minor ports.

Question 6.
Have you heard about any stampede in your district? write about that incident briefly.
Answer:
During Athivaradhar festival minor stampede that brokeout on Thursday (18^th July 2019) the crowd flocked to Kancheepuram as it was an auspicious day after the lunar eclipse. Four people died.

On 21^st April 2019 atleast seven people died in stampede in Tamil Nadu during a temple festival at Muthuaiyampalayam Karuppusamy temple in Thuraiyur a village near Trichy (Sunday).

VI. Distinguish between the following.

Question 1.
Marine Fishing and Inland fishing
Answer:

Marine Fishing	Inland Fishing
It is carried out in oceans and seas.	Inland fishing is carried out in lakes, rivers, ponds, estuaries, backwaters and swamps.
Large mechanised boats are used for fishing.	Catamaran, diesel boats and floating nets are used in fishing.
The fish varieties caught are sharks, flying fish, counch, catfish, silver bellies and crabs.	Oysters and prawns are cultured in original nurseries.
Chennai, KanyaKumari, Tirunelveli, Nagapattinam, Thanjavur and Ramanathapuram.	Vellore, Cuddalore, Sivagangai and Virudhunagar districts are inland fish production of the state.

Question 2.
Food Crops and Non- Food Crops
Answer:

Food Crops	Non- Food Crops
Food crops are mainly grown for consumption	They are mainly grown for sale purpose
Paddy is the main food crop and cereals, pulses and millets are also the second staple food of the people of Tamil Nadu	Sugarcane, cotton, tree and coffee
Cauvery delta is known as the Granary of South India leading in rice cultivation	Tiruvallur, Kancheepuram, Vellore, coimbatore, Cuddalore, Erode, Madurai, Ramanatha Puram, Salem, Thoothukudi, Nilgiris and yercaud.

Question 3.
Surface Water and Ground Water
Answer:

Surface Water	Ground Water
The total surface water potential of the state is about 24,864 mem.	The utilizable groundwater resource of the state is 22,423 mem.
There are 17 major river basins in the state with 81 reservoirs and about 41,262 tanks	The current level of utilization of water is about 13,558 mem.
Most of the surface water has already been tapped, primarily for irrigation, where water use in the largest.	60% of the available recharge, while about (8875 mcm) 40% is the balance available for use.

VII. Give reasons for the following

Question 1.
Farmers switch over from inorganic to organic farming.
Answer:
By continuous usage of chemical fertilizers, pesticides and insecticides the soil became unfit for cultivation after some years. It causes a threat to agriculture. So to bring back the soil to fertility and to make it fit for cultivation farmers switch over from inorganic to organic farming. Organic wastes, biological pest control crop residues and animal manure only used under organic farming.

Question 2.
Cities are densely populated than the villages.
Answer:
Agriculture, job opportunities and industrial development are the main causes of population density in the cities then the villages.

Question 3.
Karur is Called the Textile Capital of Tamil Nadu.
Answer:
Karur is an industry town and is very famous for cottage and hand-loom textile industries. Moreover state’s most of the textile goods exports is from Karur district. That is why Karur is called the textile capital of Tamil Nadu.

Question 4.
Mostly stampede occurs in Temples.
Answer:
Most of the religious festivals are located in areas like banks of rivers hilly terrains or mountain tops. These areas lack proper pathways, posing a geographical risk to the pilgrims. It often disrupts the orderly movement of crowds resulting in irrational and dangerous movement for self-protection, leading to injuries and fatalities. Because of the lack of physical infrastructure, the mob behaviour increases the sense of threat, which results in a stampede.

VIII. Answer the following in a paragraph.

Question 1.
Write about the plantation farming of Tamil Nadu.
Answer:
Plantation Crops: Tea, coffee, cashew, rubber, pepper and cinchona.

The hill slopes with laterite soil and acidic-nature is ideal for the plantation crops.

Tea: Tea plantations are found in the hills of the Nilgins and Coimbatore. Notable region for tea estates Nilgiris.

Coffee: Coffee plants are grown in the hills of Western Ghats as well as Eastern Ghats. It is also found in the hilly slopes of Dindigui, Madurai, Theni and Salem districts.
Notable places: Yercaud, Kolli hills and Kodaikanal,

Rubber: Rubber plantations are significant in Kanyakumari.

Cashew: It is extensively cultivated in Cuddalore district.

Pepper: Confined to the warm and wet slopes of Eastern and Western Ghats of Tamil Nadu.

Cinchona: It is planted at heights varying from 1060 to 1280 metres in Anaimalai hills.

Cardamom: Cardamom estates are located at few places in the hills of Madurai region at an elevation of 915 to 1525 metres.

Position: Tamil Nadu stands second in area and production of tea and coffee next to Assam and Karnataka respectively.

Question 2.
Give an account on water resources of Tamil Nadu.
Answer:

1. Tamil Nadu constitutes 4% of India’s land area and is inhabited by 6% of India’s population, but has-only 2.5% of India’s water resources.
2. More than 95% of the surface water and 80% of the ground water have already been put into use.
3. Major uses of water include human/animal consumption irrigation and industrial use.
4. The state is heavily dependent on monsoon rains.
5. The annual average rainfall is around 930 mm (47% during the northeast monsoon, 35% during the south west monsoon, 14% in summer and 4% in winter.
   

Question 3.
Bring out the mineral distribution in Tamil Nadu.
Answer:
(i) Tamil Nadu is the leading holder of country’s resources of vermiculite, magnetite, dunite, rutile, garnet, molybdenum and ilmenite.

(ii) The state accounts for the country’s 55.3% of lignite, 75% of vermiculite, 69% of dunite, 59% of garnet, 52% of molybdenum and 30% of titanium mineral resources.
Important minerals are found in the state are as follows:

1. Neyveli has large lignite resources.
2. Coal is available in Ramanathapuram
3. Oil gas are found in the Cauvery basin
4. Iron deposits are found in Kanjamalai region in Salem district and Kalrayan Malai region of Tiruvannamalai district.
5. Magnesite ores are available near Salem.
6. Bauxite is found in Servarayan Hills, Kotagiri, Udagamandalam, Palani and Kollimalai areas.
7. Gypsum is obtained in Tiruchirappalli, Tirunelveli, Thoothukudi and Virudhunagar districts.
8. Ilmenite and rutile are found in the sands of Kanyakumari beach.
9. Limestone is available in Coimbatore, Cuddalore, Dindigul, Kancheepuram, Karur, Madurai, Nagapattinam, Namakkal, Perambalur, Ramanathapuram, Salem and Tiruvallur districts.
10. Magnesite is obtained in Coimbatore, Dharmapuri, Karur, Namakkal, the Nilgiris, Salem.
11. Feldspar, quartz, copper and lead are found in some parts of the state.

Question 4.
State the densely populated regions of Tamil Nadu and account for its high density.
Answer:

1. The number of persons living per square km is referred as population density.
2. A place is said to have high density of population if number of persons living per sq km is above 800.
3. As per 2011 census the density of population in Tamil Nadu is 555 per sq.km

Densely populated regions of Tamil Nadu:
Chennai is the densest district – 26,903 persons per sq.km followed by Kanyakumari (1106), Tiruvallur (1049), Kancheepuram (927), Madurai (823), Coimbatore (748), Cuddalore (1702), Thanjavur (691), Nagapattinam (668-), Salem (663), Vellore (646), Tiruchirappalli (602).

Question 5.
Explain the different modes of transport available in Tamil Nadu.
Answer:
Roadways:
The State has a total road length of 167,000 km, In which 60,628km are maintained by state Highways Department. It ranks second in India with a share of over 20% in total road projects under operation in the Public-Private Partnership (PPP) model.

Railways:

• Tamil Nadu has a well-developed rail network as part of Southern Railway, headquartered at Chennai.
  The present Southern Railway network extends over a large area of India’s southern peninsula, covering Tamil Nadu, Kerala, Puducherry, minor portions of Karnataka and Andhra Pradesh.
• Tamil Nadu has a total railway track length of 6,693 km with 690 railway stations in the state.
• The system connects it with most of the major cities in India.
• Main rail junctions in the state include Chennai, Coimbatore, Erode, Madurai, Salem, Tiruchirappalli and Tirunelveli.
• Chennai has a well-established suburban railway network, a Mass Rapid Transport System (MRTS) and is currently developing a Metro system, with its first underground stretch in operation since May 2017.

Airways:

• Tamil Nadu has four major international airports. Chennai International Airport is currently the third largest airport in India after Mumbai and Delhi.

Water ways:

• Tamil Nadu has 3 major ports. They are Chennai, Ennore and Tuticorin. It has an intermediate port at Nagapattinam and 15 minor ports. Ennore intermediate port was recently converted as a major port and handles the major coal and ore traffics in Tamil Nadu.

Question 6.
Write about Road safety rules.
Answer:
In recent years the number of road accidents in Tamil Nadu has been increasing. It is reported that 15% of the road accidents of the country takes place in Tamil Nadu.

Basic road safety rules:

1. Aware of the road signals
2. Stop, look and cross
3. Listen and ensure whether a vehicle is approaching
4. Don’t rush on roads
5. Crossroads in pedestrian crossings
6. Don’t stretch hands while driving vehicles.
7. Never crossroad at bends and stay safe in a moving vehicle.
8. Avoid speeding, Drunk and driving, use helmets and seat belts and follow traffic rules.

“Know – Risk! No – risk!”

IX. Map Study

Question 1.
Mark the areas of major crops, minerals, dams, airport and seaports.
Answer:

Human Geography of Tamil Nadu Additional Questions

I. Choose the correct answer.

Question 1.
Tea, Coffee, rubber, pepper and cashew are …………. crops.
(a) Food
(b) Fiber
(c) Plantation
Answer:
(c) Plantation

Question 2.
The word Agriculture is derived from the ……………….. words “ager and Cultura”.
(a) Latin
(b) Greek
(c) Tamil
(d) Spanish
Answer:
(a) Latin

Question 3.
Rice, Cotton, Sugercane are grown with …………….
(a) Drying farming
(b) Irrigation farming
(c) Cattle reasing
Answer:
(b) Irrigation farming

Question 4.
In Tamil Nadu Rice Research Institute is situated at:
(a) Aduthurai
(b) Madurai
(c) Thiruvallur
(d) Chennai
Answer:
(a) Aduthurai

Question 5.
Millets are ……………… crops.
(a) Wet crops
(b) Dry crops
(c) Plantation
Answer:
(b) Dry crops

Question 6.
To promote ……………….. a central scheme named ‘National Project on Organic Farming’was launched.
(a) mixed farming
(b) organic farming
(c) aquaculture
(d) plantation farming
Answer:
(b) organic farming

Question 7.
Which is known as the Textile capital of Tamil Nadu?
(a) Salem
(b) Karur
(c) Tirunelveli
Answer:
(b) Karur

Question 8.
……………….. is also known as ‘poor man’s cow’.
(a) Goat
(b) Sheep
(c) Buffalo
(d) Horse
Answer:
(a) Goat

Question 9.
The most populated district in Tamil Nadu is …………….
(a) Madurai
(b) Tiruvallur
(c) Chennai
Answer:
(c) Chennai

Question 10.
districts lead in the Inland fish production.
(a) Chennai
(b) Cuddalore
(c) Sivagangai
(d) Vellore
Answer:
(d) Vellore

II. Fill in the blanks:

1. …………. irrigation is most predominant irrigation system in TamilNadu.
2. ……….. Dam is one of the biggest earthen dams in the country.
3. Amaravathi reservoir is notable for the …………….
4. Papanasam dam is also known as ………….. dam.
5. Parappalar project is located near …………….
6. Tamil Nadu occupies ……………… position in the country in silk production.
7. The Vellore district is the top exporter of finished …………. in the country.
8. Tamil Nadu accounts for about ………….. of India’s …………. exports.
9. Tamil Nadu ranks among the Indian states in population density.
10. ………… in considered the ‘fire works capital’ of India.
Answers:
1. Well
2. Bhavani
3. Mugger crocodiles
4. Karaiyar
5. Ottanchatram
6. Fourth
7. leather goods
8. 17%, Software
9. 12th
10. Sivakasi

III. Match the following.

a.

1.	Rearing of birds	(a)	Apiculture
2.	Rearing of honeybees	(b)	Horticulture
3.	Rearing of silkworms	(c)	Poultry farming
4.	Growing fruits	(d)	Sericulture

Answer:
1. (c)
2. (a)
3.(d)
4.(b)

b.

1.	Wet fanning	(a)	Millets
2.	Dry farming	(b)	Rice
3.	Plantation farming	(c)	Sugarcane
4.	Market gardening	(d)	Tea, Coffee
5.	Irrigation farming	(e)	Kancheepuram

Answer:
1. (b)
2. (a)
3. (d)
4. (e)
5. (c)

IV. Answer briefly:

Question 1.
What is Agriculture?
Answer:
Agriculture is a practice of farming that includes cultivation of crops, rearing of animals, birds, forestry, fisheries and other related activities.

Question 2.
What is the Multipurpose River Valley Projects?
Answer:
Multipurpose river valley projects are basically designed for the development of irrigation for agriculture and hydropower generation they are used for many other purposes as well.

Question 3.
List out the major food crops and commercial crops of the state.
Answer:

1. The principal food crops – paddy, millets and pulses.
2. The commercial crops – sugarcane, cotton, oilseeds, spices, tea, and coffee and cashew.

Question 4.
Define Trade.
Answer:
Trade-in an exchange of goods and commodities either within the country or between countries.

Question 5.
Write a note on Tamil Nadu Rice Research Institute.
Answer:

1. Tamil Nadu Rice Research Institute was established in April 1985 under Tamil Nadu Agricultural University.
2. It is situated at AduthUrai (Thanjavur).
3. It’s function is to perform lead function for rice and rice based cropping system research with the help of existing agriculture colleges and research centers.

Question 6.
Name any four districts with low density of population.
Answer:
Nilgiris, Perambalur, Dharmapuri and Sivagangai.

Question 7.
What are minor ports?
Answer:
Minor ports are anchorage ports where cargo is transhipped from the vessel to the store.
Ex. Cuddalore, Nagapattinam, Kolachal and Rameshwaram.

Question 8.
What are the uses of Chinchona?
Answer:

• Chinchona is a forest product.
• From chinchona quinine a drug is extracted.
• Malaria is treated with this medicine.

Question 9.
Write the expansion of these abbreviated terms.

1. TNAU
2. TANTEA
3. TNPL
4. TANCEM
5. Gl
6. CLRI
7. SEZ
8. TTDC

Answer:

1. TNAU: Tamil Nadu Agriculture University
2. TANTEA: Tamil Nadu Tea Plantation Corporation Limited
3. TNPL: Tamil Nadu Newsprint and Papers Limited
4. TANCEM: Tamil Nadu Cements Corporation Limited
5. GI: Geographical Indication
6. CLRI: Central Leather Research Institute –
7. SEZ: Special Economic Zone
8. TTDC: Tamil Nadu Tourism-Development Corporation

Question 10.
Name the factors influencing agriculture.
Answer:
The factors influencing agriculture can be classified as Physical, Social and economic factors.

• Physical factors includes soil, temperature, rainfall, humidity, climate and slope of land.
• The social factors includes traditional knowledge belief and myths of farmers, farm size and holdings and fanners acceptance towards innovation.
• Economic factors are market loan assistance, government subsidy and incentives.

V. Distinguish:

Question 1.
Wet farming and Dry farming
Answer:

Wet farming	Dry farming
Water supply is available through out the year from rain fall and irrigation for farming.	Farming is carried out only during rainy season.
Rice and sugarcane are grown.	Ragi and millets are grown.

Question 2.
Commercial crops and Plantation crops
Answer:

Commercial crops	Plantation crops
Sugarcane, tobacco, oil seeds, spices, turmeric etc are commercial crops.	Tea, coffee, rubber, pepper and cashewnut are the main plantation crops.
Tobacco is yet another commercial crop grown an Dindigul, Teni and Madurai districts.	Coffee in grown in the W.Ghats and E. Ghats.

Question 3.
Imports and Exports
Answer:

Imports	Exports
Goods and services bought from overseas producers.	Goods and services sold to overseas consumers.
A country that imports goods and services loses foreign exchage currency.	A country that exports goods and services gains foreign exchange currency.
Tamil Nadu imports machineries, electrical equipments, mineral, fuel and pharmaceutical products.	Tamil Nadu exports agricultural products, Leather products, Gems, and jewellery, chemical and related products.

VI. Answer the following in detail.

Question 1.
Tourism is considered as an industry – justify. Give an account on Tourism in Tamil Nadu.
Answer:

1. Tourism is considered as an industry because of its enormous potential in creating employment for a large number of people.
2. Approximately 28 lakh foreign and 11 crore domestic tourists visit our state (Tamil Nadu) annually.
3. Reasons: The presence of ancient temples and monuments, hill stations pilgrim centres, a variety of natural land scapes, long coast line along with rich culture and heritage make Tamil Nadu the best destination for tourists.
4. Promoter: Tourism in Tamil Nadu is promoted by Tamil Nadu Tourism Development Corporation (TTDC).
5. The state currently ranks the highest among Indian states with about 25 crore arrivals (in 2013).

Question 2.
Give an account for the distribution of Textile industry in Tamil Nadu.
Answer:
Textile industry is one of the traditionally well-developed industries in Tamil Nadu. Tamil Nadu has a major share in the Indian Textile industry in terms of production and export of yams, fabrics, knitwear and garments. Tamil Nadu contributes 30% of India’s share in export of cotton, yam and fabrics.

Tropical climate availability of raw materials, demand for cotton in market, power supply from numerous power projects and abundant cheap labour are favourable factors for widespread distribution of textile industries in Tamil Nadu. The textile mills are concentrated in Coimbatore, Tirupur, Salem, Palladam, Kamr, Dindigul, Vimdhunagar, Tirunelveli, Thoothukudi, Madurai and Erode. Tamil Nadu has about 3,50,000 power looms manufacturing cotton fabrics.

Maximum units are concentrated in and around Coimbatore region for this region it is known as the “Manchester of South India”. Timpur and Erode contributes much for the state economy, therefore they are referred to as ‘Textile Valley of Tamil Nadu’.

Timpur alone contributes 70% of export of knitwear of Tamil Nadu. Erode specializes in garments and bedspreads. The city of Kamr is known as ‘Textile capital of Tamil Nadu Silk Textiles’. Tamil Nadu occupies fourth place in silk textile production in our country Kancheepuram silk is unique in its quality and is known for its traditional value all over the world. Arani, Rasipuram and Thimbuvanam are other silk centres of Tamil Nadu.

Sericulture Training Institute in Hosur training farmers to adopt agriculture along with farm work to accelerate rural industrialization Mettur, Madurai and Ramanathapuram are specialized areas for manufacturing synthetic clothes.