Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.4

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.4

Question 1.
By the principle of mathematical induction, prove that, for n ≥ 1

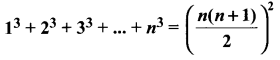
Solution:

∴ P(k+ 1) is true.
Thus P(K) is true ⇒ (k + 1) is true.
Hence by principle of mathematical induction, P(n) is true for all n ∈ N.

Question 2.
By the principle of mathematical induction, prove that, for n > 1

Solution:

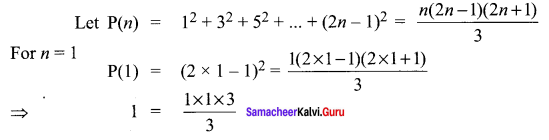
∴ P(1) is true
Let P(n) be true for n = k

∴ P(k + 1) is true
Thus P(k) is true ⇒ P(k + 1) is true. Hence by the principle of mathematical induction, P(k) is true for all n ∈ N.

Question 3.
Prove that the sum of the first n non-zero even numbers is n² + n.
Solution:
Let P(n) = 2 + 4 + 6 + ………….. + 2n = n² + n

Step 1:
Let us verify the statement for n = 1
P (1 ) = 2 = 1² + 1 = 1 + 1 = 2.
∴ The given result is true for n = 1.

Step 2:
Let us assume that the given result is true for n = k
P ( k) = 2 + 4 + 6 + ………… + 2k = k² + k

Step 3:
Let us prove the result for n = k + 1
P (k+ 1 ) = 2 + 4 + 6+ + 2k + (2k + 2 )
P(k+ 1 ) = P(k) + (2k + 2)
= k² + k + 2k + 2
= k² + 3k + 2
= k² + 2k + k + 2
= k(k +2) + 1(k + 2)
P(k+ 1 ) = (k+ 1) (k + 2) ……….. (1)
P (k) = k² + k
= k (k + 1 )
P(k+ 1) = (k + 1) (k + 1 + 1)
= (k + 1) (k + 2)
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
2 + 4 + 6 + ………….. + 2n = n² + n
is true for all natural numbers n.

Question 4.
By the principle of Mathematical induction, prove that, for n ≥ 1.

Solution:


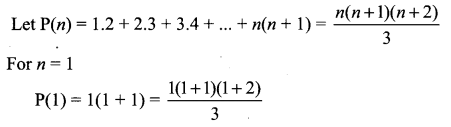
∴ P(k + 1) is true
Thus P(k) is true ⇒ P(k + 1) is true
Hence by the principle of mathematical induction, P(n) is true for all n ∈ N

Question 5.
Using the Mathematical induction, show that for any natural number n ≥ 2,

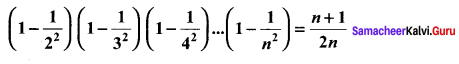
Solution:


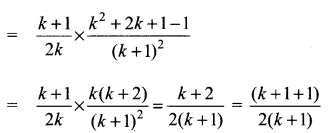
⇒ P(k + 1) is true when P(k) is true so by the principle of mathematical induction P(n) is true.

Question 6.
Using the Mathematical induction, show that for any natural number n ≥ 2,

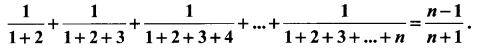
Solution:


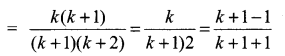
⇒ P(k + 1) is true when P(k) is true so by the principle of mathematical induction P(n) is true for n ≥ 2.

Question 7.
Using the Mathematical induction, show that for any natural number n

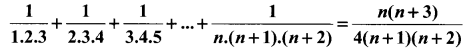
Solution:


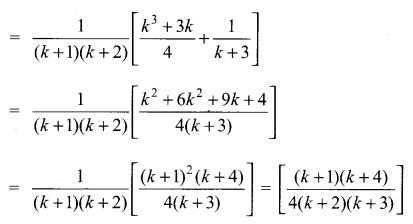
∴ P(k + 1) is true
Thus p(k) is true ⇒ P(k + 1) is true
Hence by the principle of mathematical induction,
p(n) is true for all n ∈ z

Question 8.
Using the Mathematical induction, show that for any natural number n,

Solution:


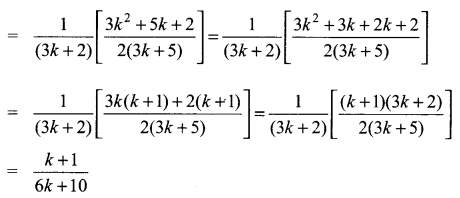
∴ P(k + 1) is true
Thus P(k) is true ⇒ P(k + 1) is true. Hence by the principle of mathematical induction, P(n) is true for all n ∈ N.

Question 9.
Prove by Mathematical Induction that
1! + (2 × 2!) + (3 × 3!) + … + (n × n!) = (n + 1)! – 1
Solution:
Let p(n) = 1! + (2 × 2 !) + (3 × 3!) +…. .+ (n × n!) = (n + 1)! – 1

Step 1:
First let us verify the result for n = 1
P(1) = 1! = (1 + 1)! – 1
P(1) = 1! = 2! – 1
P(1) = 1 = 2 – 1 = 1
∴ We have verified the result for n = 1.

Step 2:
Let us assume that the result is true for n = k
P(k) = (1 × 1 !) + (2 × 2!) + (3 × 3!) + …………. + (k × k!) = (k + 1)! – 1

Step 3:
Let us prove the result for n = k + 1
P(k + 1)=(1 × 1!) + (2 × 2!) + (3 × 3!) + ………….. + (k × k!) + ((k + 1) × (k + 1)!)
P(k + 1) = P(k) + ((k + 1) × (k + 1)!)
P(k + 1) = (k + 1)! – 1 + (k + 1) × (k + 1)!
= (k + 1)! + (k + 1) (k + 1)! – 1
= (k + 1)! (1 + k + 1) – 1
= (k + 1)! (k + 2) – 1
= (k + 2)! – 1
P(k + 1) = ((k + 1) + 1)! – 1
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
(1 × 1!) + (2 × 2!) + (3 × 3!) + …………… + (n × n!) = (n + 1)! – 1
is true for all natural numbers n.

Question 10.
Using the Mathematical induction, show that for any natural number n, x²ⁿ – y²ⁿ is divisible by x +y.
Solution:
Let P(n) = x²ⁿ – y²ⁿ is divisible by x + y
Step 1:
First, let us verify the result for n = 1.
P ( 1 ) = x²⁽¹⁾ – y²⁽¹⁾ = x² – y²
P(1) = (x + y) (x – y) which is divisible by x + y
∴ The result is true for n = 1

Step 2:
Let us assume that the result is true for n = k
P(k) = x^2k – y^2k which is divisible by x + y
∴ P (k) = x^2k – y^2k = λ (x + y) where λ ∈ N ——— (1)

Step 3:
Let us prove the result for n = k + 1

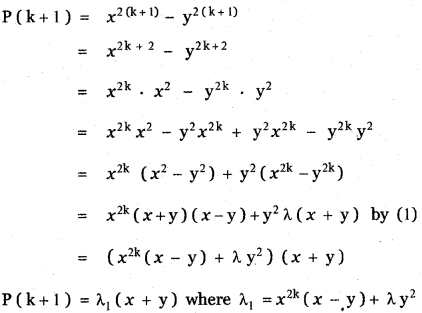
∴ P ( k + 1) is divisible by x + y
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
x²ⁿ – y²ⁿ is divisible by x + y
for all natural numbers n.

Question 11.
By the principle of mathematical induction, prove that, for n ≥ 1,

Solution:

Question 12.
Use induction to prove that n³ – 7n + 3, is divisible by 3, for all natural numbers n.
Solution:
Let P ( n) = n³ – 7n + 3 is divisible by 3

Step 1:
First let us verify the results for n = 1
P(I) = 1³ – 7 × 1 + 3
= 1 – 7 + 3
P (1) = – 3
which is divisible by 3
∴ The result is true for n = 1

Step 2:
Let us assume that the result is true for n = k
P(k) = k³ – 7k + 3 is divisible by 3
P(k) = k³ – 7k + 3 = 3λ where λ ∈ N

Step 3:
Let us prove the result for n = k + 1
P(k + 1) = (k + 1)³ – 7(k + 1 ) + 3
= k³ + 3k² + 3k + 1 – 7k – 7 + 3
= k³ + 3k² – 4k – 3
= k³ – 4k – 3k + 3k – 3 + 6 – 6 + 3k²
= k³ – 7k + 3 + 3k – 6 + 3k²
= (k³ – 7k + 3) + 3(k² + k – 2)
= 3λ + 3 (k² + k – 2)
P(k + 1) = 3 (λ + k² + k – 2 )
which is a multiple of 3, hence divisible by 3
This implies P (k + 1) is true.
∴ Thus, we have proved the result for n = k + 1.
Hence by the principle of mathematical induction, the result is true for all natural numbers n.
n³ – 7n + 3 is divisible by 3 for all natural numbers n.

Question 13.
Use induction to prove that 5^{n + 1} + 4 × 6ⁿ when divided by 20 leaves a remainder 9, for all natural numbers n.
Solution:
P(n) is the statement 5^{n + 1} + 4 × 6ⁿ – 9 is ÷ by 20
P(1) = 5^{1 + 1} + 4 × 6¹ – 9 = 5² + 24 – 9
= 25 + 24 – 9 = 40 ÷ by 20
So P(1) is true
Assume that the given statement is true for n = k
(i.e) 5^{k + 1} + 4 × 6ⁿ – 9 is ÷ by 20
P(1) = 5^{1 + 1} + 4 × 6¹ – 9
= 25 + 24 – 9
So P(1) is true
To prove P(k + 1) is true
P(k + 1) = 5^{k + 1 + 1} + 4 × 6^{k + 1 + 1} – 9
= 5 × 5 ^{k + 1} + 4 × 6 × 6^k – 9
= 5[20C + 9 – 4 × 6^k] + 24 × 6^k – 9 [from(1)]
= 100C + 45 – 206^k + 246^k – 9
= 100C + 46^k + 36
= 100C + 4(9 + 6^k)
Now for k = 1 ⇒ 4(9 + 6^k) = 4(9 + 6)
= 4 × 15 = 60 ÷ by 20 .
for k = 2 = 4(9 + 6²) = 4 × 45 = 180 ÷ 20
So by the principle of mathematical induction 4(9 + 6^k) is ÷ by 20
Now 100C is ÷ by 20.
So 100C + 4(9 + 6^k) is ÷ by 20
⇒ P(k + 1) is true whenever P(k) is true. So by the principle of mathematical induction P(n) is true.

Question 14.
Use induction to prove that 10ⁿ + 3 × 4^{n + 2} + 5, is divisible by 9, for all natural numbers n.
Solution:
P(n) is the statement 10ⁿ + 3 × 4^{n + 2} + 5 is ÷ by 9
P(1) = 10¹ + 3 × 4² + 5 = 10 + 3 × 16 + 5
= 10 + 48 + 5 = 63 ÷ by 9
So P(1) is true. Assume that P(k) is true
(i.e.) 10^k + 3 × 4^{k + 2} + 5 is ÷ by 9
(i.e.) 10^k + 3 × 4^{k + 2} + 5 = 9C (where C is an integer)
⇒ 10^k = 9C – 5 – 3 × 4^{k + 2} ……(1)
To prove P(k + 1) is true.
Now P(k + 1) = 10^{k + 1} + 3 × 4^{k + 3} + 5
= 10 × 10^k + 3 × 4^{k + 2} × 4 + 5
= 10[9C – 5 – 3 × 4^{k + 2}] + 3 × 4^{k + 2} × 4 + 5
= 10[9C – 5 – 3 × 4^{k + 2}] + 12 × 4^{k + 2} + 5
= 90C – 50 – 30 × 4^{k + 2} + 12 × 4^{k + 2} + 5
= 90C – 45 – 18 × 4^{k + 2}
= 9[10C – 5 – 2 × 4^{k + 2}] which is ÷ by 9
So P(k + 1) is true whenever P(K) is true. So by the principle of mathematical induction P(n) is true.

Question 15.
Prove that using the Mathematical induction

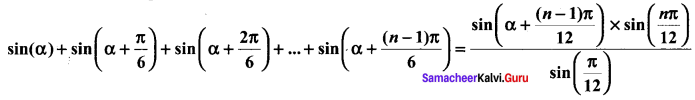
Solution:

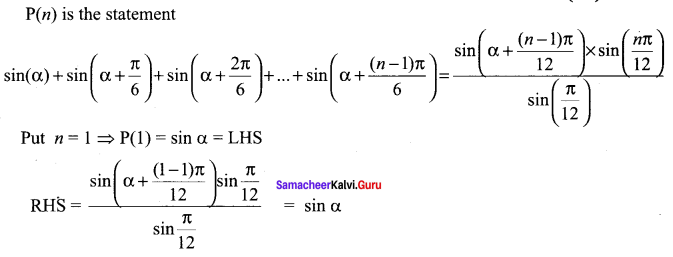
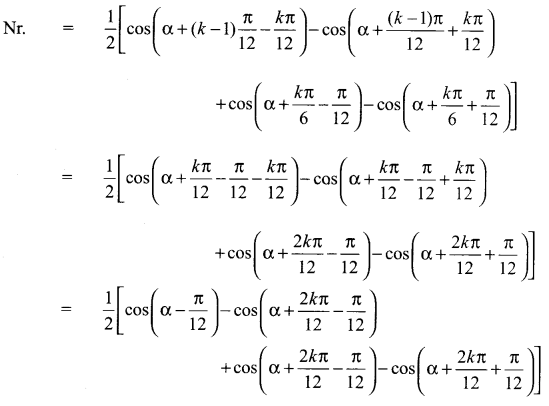
Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.4 Additional Questions

Question 1.
Prove by induction the inequality (1 + x)ⁿ ≥ 1 + nx, whenever x is positive and n is a positive integer.
Solution:
P(n) : (1 +x)ⁿ ≥ 1 +nx
P(1): (1 + x)¹ ≥ 1 + x
⇒ 1 + x ≥ 1 + x, which is true.
Hence, P(1) is true.
Let P(k) be true
(i.e.) (1 + x)^k ≥ 1 + kx
We have to prove that P(k + 1) is true.
(i.e.) (1 + x)^{k + 1} ≥ 1 + (k + 1)x
Now, (1 + x)^{k + 1} ≥ 1 + kx [∵ p(k) is true]
Multiplying both sides by (1 + x), we get
(1 + x)^k(1 + x) ≥ (1 + kx)(1 + x)
⇒ (1 + x)^{k + 1} ≥ 1 + kx + x + kx²
⇒ (1 + x)^{k + 1} ≥ 1 + (k + 1)x + kx² ….. (1)
Now, 1 + (k + 1) x + kx² ≥ 1 + (k + 1)x …… (2)
[∵ kx² > 0]
From (1) and (2), we get
(1 + x)^{k + 1} ≥ 1 + (k + 1)x
∴ P(k + 1) is true if P(k) is true.
Hence, by the principle of mathematical induction, P(n) is true for all values, of n.

Question 2.
3²ⁿ – 1 is divisible by 8.
Solution:
P(n) = 3²ⁿ – 1 is divisible by 8
For n = 1, we get
P(1) = 3^2.1 – 1 = 9 – 1 = 8
P(1) = 8, which is divisible by 8.
Let P(n) be true for n = k
P(k) = 3^2k – 1 is divisible by 8 ….. (1)
Now, P(k + 1) = 3^{(2k + 2)} – 1 = 3^2k.3² – 1
= 3²(3^2k – 1) + 8
Now, 3^2k – 1 is divisible by 9. [Using (1)]
∴ 3² (3^2k – 1) + 8 is also divisible by 8.
Hence, 3²ⁿ – 1 is divisible by 8 ∀ n E N

Question 3.
Prove by the principle of mathematical induction if x and y are any two distinct integers, then xⁿ – yⁿ is divisible by x – y. [OR]
xⁿ – yⁿ is divisible by x – y, where x – y ≠ 0.
Solution:
Let the given statement be P(n).
(i.e.) P(n): xⁿ – yⁿ = M(x – y), x – y ≠ 0

Step I.
When n = 1,
xⁿ – yⁿ = x – y = M(x – y) ….(1)
⇒ P(1) is true.

Step II.
Assume that P(k) is true.
(i.e.) x^k – y^k = M(x – y), x – y ≠ 0
We shall now show that P(k + 1) is true
Now, x^{k + 1} – y^{k + 1} = x^{k + 1} – x^ky + x^{k + 1}y – y^{k + 1}
= x^k(x – y) + y(x^k – y^k)
= x^k(x – y) + yM(x – y) [Usng ….. (1)]
= (x – y)(x^k – yM)
∴ By the principle of mathematical induction, P(n) is true for all n ∈ N

Question 4.
Prove by the principle of mathematical induction that for every natural number n, 3^{2n + 2} – 8n – 9 is divisible by 8.
Solution:
Let P(n): 3^{2n + 2} – 8n – 9 is divisible by 8.
Then, P(1): 3^{2.1 + 2} – 8.1 – 9 is divisible by 8.
(i.e.) 3⁴ – 8 – 9 is divisible by 8 or 81 – 8 – 9 is divisible by 8
(or) 64 is divisible by 8, which is true.
Suppose P(k) is true, then
P(k) : 3^{2k + 2} – 8k – 9 is divisible by 8
(i.e.) 3^{2k + 2} – 8k – 9 = 8m, where m ∈ N (or)
3^{2k + 2} = 8m + 8k + 9
P(k + 1) is the statement given by, …(1)
P(k + 1) : 3^{2(k + 1) + 2} – 8(k + 1) – 9

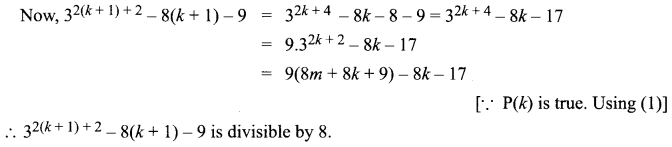
∴ P(k + 1) is true
Hence, by the principle of mathematical induction, P(n) is true for all n ∈ N

Question 5.
Use the principle of mathematical induction to prove that for every natural number n.

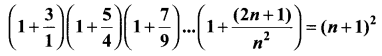
Solution:
Let P(n) be the given statement, i.e.

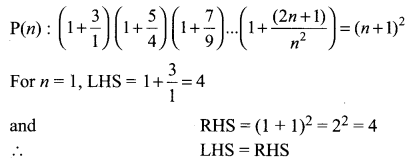
⇒ P(1) is true.
We note that P(n) is true for n = 1.
Assume that P(k) is true

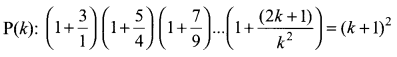
Now, we shall prove that P(k + 1) is true whenever P(k) is true. We have,

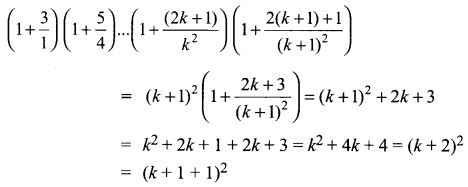
∴ P(k + 1) is also true whenever P(k) is true
Hence, by the principle of mathematical induction, P(n) is also true for all n ∈ N.

Question 6.
n³ – n is divisible by 6, for each natural number n ≥ 2.
Solution:
Let P(n) : n³ – n

Step 1 :
P(2): 2³ – 2 = 6 which is divisible by 6. So it is true for P(2).

Step 2 :
P(A): k³ – k = 6λ. Let it is be true for k ≥ 2
⇒ k³ = 6λ + k …(i)

Step 3 :
P(k + 1) = (k + 1)³ – (k + 1)
= k³ + 1 + 3k² + 3k – k – 1 = k³ – k + 3(k² + k)
= k³ – k + 3(k² + k) = 6λ + k – k + 3(k² + k)
= 6λ + 3(k² + k) [from (i)]
We know that 3(k² + k) is divisible by 6 for every value of k ∈ N.
Hence P(k + 1) is true whenever P(k) is true.

Question 7.
For any natural number n, 7ⁿ – 2ⁿ is divisible by 5.
Solution:
Let P(n) : 7ⁿ – 2ⁿ

Step 1:
P(1) : 7¹ – 2¹ = 5λ which is divisible by 5. So it is true for P(1).

Step 2:
P(k): 7^k – 2^k = 5λ. Let it be true for P(k)

Step 3:
P(k + 1) = 7^{k + 1} – 2^{k + 1}

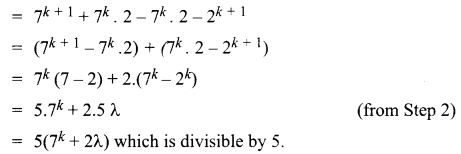
So, it is true for P(k + 1)
Hence, P(k + 1) is true whenever P(k) is true.

Question 8.
n² < 2ⁿ, for all natural numbers n ≥ 5.
Solution:
Let P(n) : n² < 2ⁿ for all natural numbers, n ≥ 5

Step 1 :
P(5) : 1⁵ < 2⁵ ⇒ 1 < 32 which is true for P(5)

Step 2 :
P(k): k² < 2k. Let it be true for k ∈ N

Step 3 :
P(k + 1): (k + 1)² < 2^{k + 1}
From Step 2, we get k² < 2^k
⇒ k² < 2^{k + 1} < 2k + 2k + 1


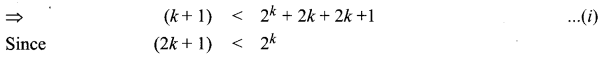
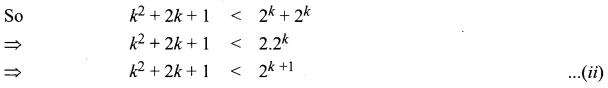
From eqn. (i) and (ii), we get (k + 1)² < 2^{k + 1}
Hence, P(k + 1) is true whenever P(k) is true for k ∈ N, n ≥ 5.

Question 9.
In 2n < (n + 2)! for all natural number n.
Solution:
Let P(n) : 2n < (n + 2)! for all k ∈ N.

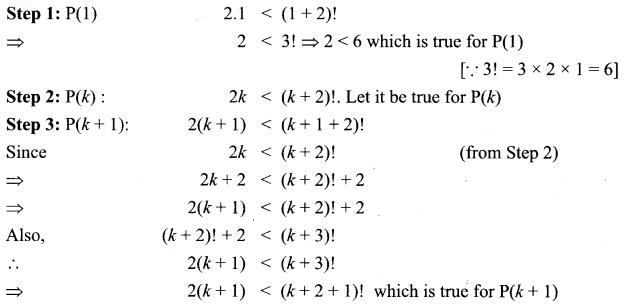
Hence, P(k + 1) is true whenever P(k) is true.

Question 10.
1 + 5 + 9 + … + (4n – 3) = n(2n – 1), ∀ n ∈ N.
Solution:
Let P(n) : 1 + 5 + 9 + … + (4n – 3) = n(2n – 1), ∀ n ∈ N

Step 1:
P(1) : 1 = 1(2.1 – 1) = 1 which is true for P(1)

Step 2:
P(k) : 1 + 5 + 9 + … + (4k – 3) = k(2k – 1). Let it be true.

Step 3:
P(k + 1) : 1 + 5 + 9 + … + (4k – 3) = k(4k + 1)
= k(2k – 1) + (4k + 1) = 2k² – k + 4k + 1
= 2k² + 3k + 1 = 2k² + 2k + k + 1
= 2k(k + 1) + 1 (k + 1) = (2k + 1)(k + 1)
= (k+ 1) (2k + 2 – 1) = (k + 1) [2(k + 1) – 1]
Which is true for P(k + 1).
Hence, P(k + 1) is true whenever P(k) is true.