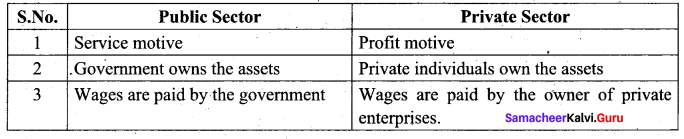
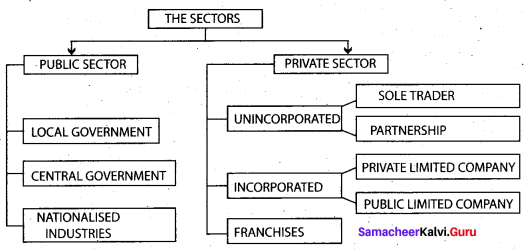
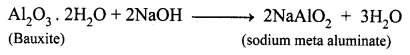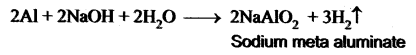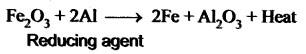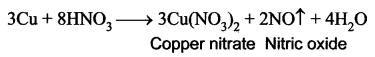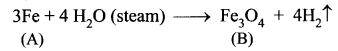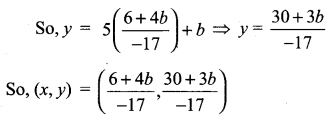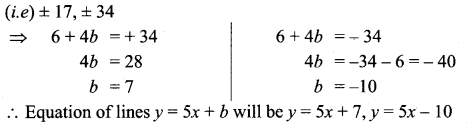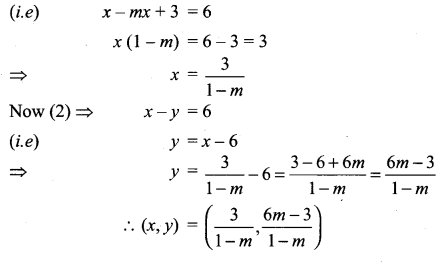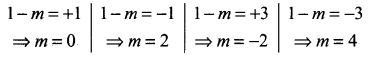You can Download Samacheer Kalvi 10th Science Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Science Solutions Chapter 8 Periodic Classification of Elements
Samacheer Kalvi 10th Science Periodic Classification of Elements Textual Evaluation Solved
I. Choose the best answer.
Question 1.
The number of periods and groups in the periodic table are ____.
(a) 6, 16
(b) 7, 17
(c) 8, 18
(d) 7, 18.
Answer:
(d) 7, 48.
Question 2.
The basis of modern periodic law is:
(a) atomic number
(b) atomic mass
(c) isotopic mass
(d) number of neutrons
Answer:
(a) atomic number
Question 3.
_____ group contains the member of the halogen family.
(a) 17th
(b) 15th
(c) 18th
(d) 16th.
Answer:
(a) 17th
Question 4.
……….is a relative periodic property.
(a) atomic radii
(b) ionic radii
(c) electron affinity
(d) electronegativity
Answer:
(d) electronegativity
Question 5.
Chemical formula of rust is ____.
(a) FeO.xH2O
(b) FeO4.xH2O
(c) Fe2O3.xH2O
(d) FeO.
Answer:
(c) Fe2O3.xH2O
Question 6.
In the aluminothermic process the role of Al is ____.
(a) oxidizing agent
(b) reducing agent
(c) hydrogenating agent
(d) sulphurising agent.
Answer:
(b) reducing agent

Question 7.
The process of coating the surface of metal with a thin layer of zinc is called:
(a) painting
(b) thinning
(c) galvanization
(d) electroplating
Answer:
(c) galvanization
Question 8.
Which of the following have inert gases 2 electrons in the outermost shell?
(a) He
(b) Ne
(c) Ar
(d) Kr.
Answer:
(a) He
Question 9.
Neon shows zero electron affinity due to:
(a) stable arrangement of neutrons
(b) stable configuration of electrons
(c) reduced size
(d) increased density
Answer:
(b) stable configuration of electrons
Question 10.
____ is an important metal to form an amalgam.
(a) Ag
(b) Hg
(c) Mg
(d) Al.
Answer:
(b) Hg
II. Fill in the blanks.
Question 1.
If the electronegativity difference between two bonded atoms in a molecule is greater than 1.7, the nature of bonding is ____.
Answer:
Ionic bond.
Question 2.
____ is the longest period in the periodical table.
Answer:
Sixth period.
Question 3.
______ forms the basis of modem periodic table.
Answer:
Atomic number.
Question 4.
If the distance between two Cl atoms in Cl2 molecule is 1.98 Å, then the radius of the Cl atom is ____.
Answer:
0.99 Å.

Question 5.
Among the given species A–, A+, and A, the smallest one in size is ______.
Answer:
A+.
Question 6.
The scientist who propounded the modem periodic law is ______.
Answer:
Henry Moseley.
Question 7.
Across the period, ionic radii ______ (increases,decreases)
Answer:
Decreases.
Question 8.
_______ and ______ are called inner transition elements.
Answer:
Lanthanides and Actinides.
Question 9.
The chief ore of Aluminium is ______.
Answer:
Bauxite (Al2O3.2H2O).
Question 10.
The chemical name of rust is ______.
Answer:
Hydrated ferric oxide.
III. Match the following.
Question 1.
| 1. Galvanisation |
(a) Noble gas elements |
| 2. Calcination |
(b) Coating with Zn |
| 3. Redox reaction |
(c) Silver-tin amalgam |
| 4. Dental filling |
(d) Alumino thermic process |
| 5. Group 18 elements |
(e) Heating in the absence of air |
Answer:
1 – (b), 2 – (e), 3 – (d), 4 – (c), 5 – (a).
IV. True or False: (If false give the correct statement)
Question 1.
Moseley’s periodic table is based on atomic mass.
Answer:
False.
Correct Statement: Moseley’s periodic table is based on atomic number.
Question 2.
Ionic radius increases across the period from left to right.
Answer:
False.
Correct Statement: Ionic radius decreases across the period from left to right.

Question 3.
All ores are minerals, but all minerals cannot be called as ores.
Answer:
True.
Question 4.
Al wires are used as electric cables due to their silvery – white colour.
Answer:
False.
Correct Statement: Al wires are used as electric cables due to their good conductor of electricity.
Question 5.
An alloy is a heterogeneous mixture of metals.
Answer:
False.
Correct Statement: An alloy is a homogenous mixture of metals.
V. Assertion and Reason:
Answer the following questions using the data given below.
(i) A and R are correct, R explains the A.
(ii) A is correct, R is wrong.
(iii) A is wrong, R is correct.
(iv) A and R are correct, R doesn’t explain A.
Question 1.
Assertion: The nature of bond in HF molecule is ionic
Reason: The electronegativity difference between H and F is 1.9.
Answer:
(i) A and R are correct, R explains the A.
Question 2.
Assertion: Magnesium is used to protect steel from rusting.
Reason: Magnesium is more reactive than iron.
Answer:
(i) A and R are correct, R explains the A.
Question 3.
Assertion: An uncleaned copper vessel is covered with a greenish layer.
Reason: copper is not attacked by alkali
Answer:
(iv) A and R are correct, R doesn’t explain A.
VI. Short Answer Questions.
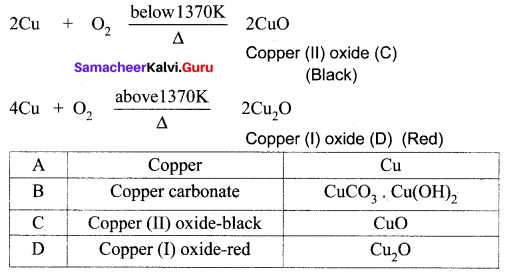
Question 1.
A is a reddish-brown metal, which combines with O2 at < 1370 K gives B, a black coloured compound. At a temperature > 1370 K, A gives C which is red in colour. Find A, B and C with reaction.
Answer:
(i) Reddish brown metal (A) is copper.
(ii) (A) reacts with O2 at bleow 1370 K gives Copper (II) oxide (B), which is black in colour.
2Cu + O2 \(\xrightarrow [ 1370k ]{ below }\) 2CuO (Copper (II) oxide) (B).
(iii) (A) reacts with O2 at above 1370 K gives Copper (I) oxide (C), which is red in colour.
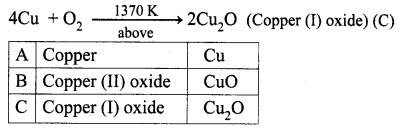
Question 2.
A is a silvery – white metal. A combines with O2 to form B at 800°C, the alloy of A is used in making the aircraft. Find A and B.
Answer:
(i) Silver – white metal (A) is Aluminium.
(ii) (A) combines with O2 to form aluminium oxide at 800°C.

(iii) Duralumin is the alloy of Al, which is used to make aircraft

Question 3.
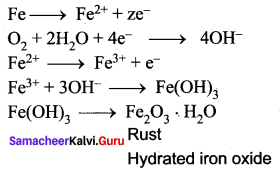
What is rust? Give the equation for formation of rust.
Answer:
Rust is hydrated ferric oxide, Fe2O3.xH2O. It is formed when iron is exposed to moist air.
4 Fe + 3O2 + xH2O > 2Fe2O3.xH2O
Question 4.
State two conditions necessary for rusting of iron.
Answer:
Conditions for rusting of iron:
- The presence of water and oxygen is essential for the rusting of iron.
- Impurities in the iron, the presence of water vapour, acids, salts and carbon dioxide hasten to rust.
- Pure iron does not rust in dry and CO2 free air. It also does not rust in pure water, free from dissolved salts.
VII. Long Answer Questions
Question 1.
(a) State the reason for the addition of caustic alkali to bauxite ore during purification of bauxite.
(b) Along with cryolite and alumina, another substance is added to the electrolyte mixture. Name the substance and give one reason for the addition.
Answer:
(a) Naturally, Bauxite is not soluble in normal solvents. Therefore the addition of caustic alkali to bauxite plays an important role while extraction of aluminium. Caustic alkali dissolves bauxite forming soluble sodium meta aluminate while impurities remain insoluble and precipitate as red mud.
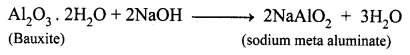
(b) Along with cryolite and alumina, another substance is added to the electrolyte mixture is Fluorspar. Adding of fluorspar lowers the fusion temperature of the electrolyte.
Question 2.
The electronic configuration of metal A is 2, 8, 18, 1. The metal A when exposed to air and moisture forms B a green layered compound. A with conc. H2SO4 forms C and D along with water. D is a gaseous compound. Find A, B, C and D.
Answer:
(i) The electronic configuration of metal (A) is 2, 8, 18, 1. A is copper (Z = 29)
(ii) (A) Copper exposed to air and moisture forms green layered compound (B) that is a copper carbonate.
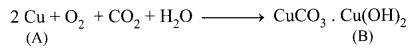
(iii) Copper (A) reacts with conc.H2SO4 to give copper sulphate (C) and Sulphur dioxide (D).
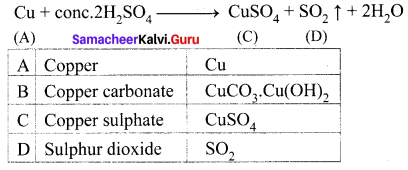
Question 3.
Explain the smelting process.
Answer:
Smelting (in a Blast Furnace): The charge consisting of roasted ore, coke and limestone in the ratio 8 : 4 : 1 is smelted in a blast furnace by introducing it through the cup and cone arrangement at the top. There are three important regions in the furnace.
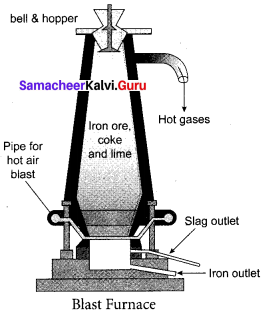
(a) The Lower Region (Combustion Zone): The temperature is at 1500°C. In this region, coke bums with oxygen to form CO2 when the charge comes in contact with a hot blast of air.
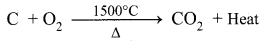
It is an exothermic reaction since heat is liberated.
(b) The Middle Region (Fusion Zone): The temperature prevails at 1000°C. In this region, CO2 is reduced to CO.
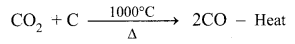
Limestone decomposes to calcium oxide and CO2
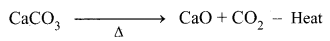
These two reactions are endothermic due to absorption of heat. Calcium oxide combines with silica to form calcium silicate slag.
CaO + SiO2 → CaSiO3
(c) The Upper Region (Reduction Zone): The temperature prevails at 400°C . In this region carbon monoxide reduces ferric oxide to form a fairly pure spongy iron.
\(\mathrm{Fe}_{2} \mathrm{O}_{3}+3 \mathrm{CO} \stackrel{400^{\circ} \mathrm{C}}{\longrightarrow} 2 \mathrm{Fe}+3 \mathrm{CO}_{2}\)
The molten iron is collected at the bottom of the furnace after removing the slag.
The iron thus formed is called pig iron. It is remelted and cast into different moulds. This iron is called cast iron.
VIII. HOT Questions.
Question 1.
Metal A belongs to period 3 and group 13. A in red hot condition reacts with steam to form B. A with strong alkali forms C. Find A, B and C with reactions.
Answer:
(i) Metal (A) belongs to period 3 and group 13, is Aluminium (Al).
(ii) (A) Al in red hot condition reacts with steam to form Aluminium oxide (B).

(iii) Aluminium (A) reacts with strong alkali forms of sodium meta aluminate (C).
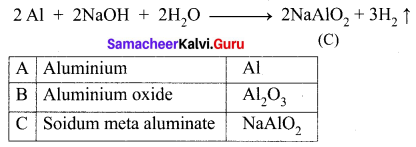
Question 2.
Name the acid that renders aluminium passive. Why?
Answer:
Dil. or cone. HNO3 does not attack aluminium, but renders Al passive due to the formation of oxide film on its surface.
Question 3.
(a) Identify the bond between H and F in the HF molecule.
(b) What property forms the basis of identification?
(c) How does the property7 vary in periods and in groups?
Answer:
(a) The nature of the bond in the HF molecule is ionic.
(b) Electronegativity.
(c) Along the period, from left to right in the periodic table the electronegativity increases because of the increase in the nuclear charge which in turn attracts the electrons more strongly. On moving down a group, the electronegativity of the elements decreases because of the increased number of energy levels.
Samacheer Kalvi 10th Science Periodic Classification of Elements Additional Questions Solved
I. Choose the best answer.
Question 1.
Which period contains only two elements?
(a) Second
(b) First
(c) Third
(d) Fifth.
Answer:
(b) First
Question 2.
The sixth period contains inner transition elements.
(a) 18
(b) 14
(c) 10
(d) 8
Answer:
(b) 14
Question 3.
Lanthanides and Actinides are called as _____.
(a) Alkali metals
(b) Inner transition elements
(c) Transition elements
(d) Representative elements.
Answer:
(b) Inner transition elements
Question 4.
The number of valence electrons present in Halogens is:
(a) One
(b) Seven
(c) Zero
(d) Two
Answer:
(b) Seven
Question 5.
The distance between the two hydrogen nuclei of the molecule is 0.74 Å. So its covalent radius is _____.
(a) 0.74 Å
(b) 0.99 Å
(c) 0.37 Å
(d) 7.4 Å.
Answer:
(c) 0.37 Å
Question 6.
Along the groups, atomic radius _____.
(a) decreases
(b) increases
(c) decreases then increase
(d) no change.
Answer:
(b) increases.
Question 7.
Which one of the following elements will have the highest electronegativity?
(a) chlorine
(b) nitrogen
(c) caesium
(d) fluorine
Answer:
(d) fluorine

Question 8.
Electron affinity is measured in _____.
(a) kJ-1
(b) mol-1
(c) kJ/mol
(d) kJ/mol2.
Answer:
(c) kJ/mol
Question 9.
Noble gases have ______ electron affinity.
(a) positive
(b) negative
(c) zero
(d) high.
Answer:
(c) zero
Question 10.
The element with positive electron gain enthalpy is:
(a) Hydrogen
(b) Sodium
(c) Argon
(d) Fluorine
Answer:
(b) Sodium
Question 11.
The mineral from which a metal can be readily and economically extracted on a large scale is said to be a / an _____.
(a) Ore
(b) Flux
(c) Slag
(d) Gangue.
Answer:
(a) Ore
Question 12.
Flux + Gangue → _____?
(a) Mineral
(b) Matrix
(c) Slag
(d) Smog.
Answer:
(c) Slag
Question 13.
………… is used for anodizing process.
(a) Zinc
(b) iron
(c) Aluminium
(d) Tin
Answer:
(c) Aluminium
Question 14.
The ore which can be purified by gravity separation method is _____.
(a) Haematite
(b) oxide ores
(c) sulphide ores
(d) both (a) and (b).
Answer:
(d) both (a) and (b).
Question 15.
The calcium silicate slag is formed in ………. zone.
(a) combustion zone
(b) fusion zone
(c) reduction
(d) molten
Answer:
(b) fusion zone
Question 16.
Zinc blende is purified by _____.
(a) Hydraulic method
(b) Magnetic separation method
(c) Froth floatation method
(d) Chemical method.
Answer:
(c) Froth floatation method
Question 17.
Bauxite ore is purified by _____.
(a) Leaching process
(b) Hydraulic method
(c) Froth floatation method
(d) Magnetic separation method.
Answer:
(a) Leaching process

Question 18.
When copper reacts with dil.HNO3 it liberates …………. gas.
(a) SO2
(b) NO2
(C) CO2
(d) NO
Answer:
(d) NO
Question 19.
Which metal process low melting point?
(a) Gallium
(b) Caesium
(c) Aluminium
(d) Copper.
Answer:
(a) Gallium
Question 20.
Which one of the following is not an ore of aluminium?
(a) Bauxite
(b) Haematite
(c) Cryolite
(d) Corundum.
Answer:
(b) Haematite
Question 21.
……….. is stored in Kerosene.
(a) Iron
(b) Silver
(c) Sodium
(d) Aluminium
Answer:
(c) Sodium
Question 22.
Electrolytic reduction of alumina into aluminium is ______.
(a) Hall’s process
(b) Alumino thermic process
(c) Baeyer’s process
(d) Bessemerisation process.
Answer:
(a) Hall’s process
Question 23.
In Hall’s process, cathode used is ______.
(a) Iron tank
(b) Graphite
(c) Pure alumina
(d) Iron tank linked with graphite.
Answer:
(d) Iron tank linked with graphite.
Question 24.
The metal oxides are usually……….. in nature.
(a) basic
(b) acidic
(c) amphoteric
(d) neither acidic nor basic
Answer:
(a) basic
Question 25.
A silvery-white metal is ______.
(a) Aluminium
(b) Copper
(c) Iron
(d) Zinc.
Answer:
(a) Aluminium
Question 26.
Aluminium reacts with NaOH to give ______.
(a) Al2O3
(b) AlCl3
(c) NaAlO2
(d) Al(OH)3
Answer:
(c) NaAlO2
Question 27.
Atoms of the elements belonging to the same group of periodic table will have:
(a) same number of protons
(b) same number of electrons in the valence shell
(c) same number of neutrons
(d) same number of electrons
Answer:
(b) same number of electrons in the valence shell
Question 28.
Chief ore of copper is ______.
(a) CuFeS2
(b) Cu2O
(c) Cu2S
(d) CuSO4
Answer:
(a) CuFeS2

Question 29.
Molecular formula for copper pyrites ______.
(a) Cu2O
(b) Cu2S
(c) CuCO3
(d) CuFeS2
Answer:
(d) CuFeS2
Question 30.
The electronegativity of fluorine is:
(a) 4.0
(b) 3
(c) 2.8
(d) 2.1
Answer:
(a) 4.0
Question 31.
The second most abundant metal available next to aluminium is ______.
(a) Cu
(b) Ag
(c) Au
(d) Fe.
Answer:
(d) Fe.
Question 32.
Most important ore of iron is ______.
(a) Haematite
(b) Magnetite
(c) Iron pyrite
(d) Cryolite.
Answer:
(a) Haematite
Question 33.
The volatile impurities present in haematite are:
(a) Carbon and Nitrogen
(b) Oxygen and Nitrogen
(c) Helium and Oxygen
(d) Sulphur and Phosphorus
Answer:
(d) Sulphur and Phosphorus
Question 34.
The solute present in brass is:
(a) copper
(b) zinc
(c) tin
(d) magnesium
Answer:
(b) zinc
Question 35.
Which one of the following is used for making pressure cookers?
(a) Brass
(b) Magnalium
(c) Duralumin
(d) Nickel steel
Answer:
(c) Duralumin
Question 36.
Which is used as propeller?
(a) Stainless steel
(b) Nickel steel
(c) Brass
(d) Magnalium.
Answer:
(b) Nickel steel
Question 37.
Gold does not occur in the combined form. It does not react with air or water. It is in the ______ state.
(a) native
(b) combined
(c) complex
(d) molten.
Answer:
(a) native
Question 38.
Which of the following metal is not found in a free state?
(a) Ag
(b) Au
(c) Pt
(d) Al.
Answer:
(d) Al.

Question 39.
Which one of the following does not react with copper?
(a) Oxygen
(b) Conc.H2SO4
(c) NaOH
(d) Conc.HNO3
Answer:
(c) NaOH
Question 40.
An element which is an essential constituent of all organic compounds belongs to ______ group.
(a) 14th
(b) 15th
(c) 16th
(d) 17th.
Answer:
(a) 14th
Question 41.
The highest ionization energy is exhibited by ______.
(a) Halogens
(b) Alkaline earth metals
(c) Transition metals
(d) Nobel gases.
Answer:
(d) Nobel gases.
Question 42.
Which two elements of the following belongs to the same period? (Al, Si, Ba, O).
(a) Si, Ba
(b) Al, Ba
(c) Al, Si
(d) Al, O.
Answer:
(c) Al, Si
Question 43.
98% pure copper and 2% impurities is called ______.
(a) Matte
(b) Copper pyrites
(c) blister copper
(d) cuprite.
Answer:
(c) blister copper
Question 44.
_____ is used in making anchors and electromagnets.
(a) Steel
(b) Pig iron
(c) Cast iron
(d) Wrought iron.
Answer:
(d) Wrought iron.
Question 45.
Which reagent does not react with iron?
(a) Conc. HNO3
(b) Conc.H2SO4
(c) Steam
(d) Dil. HNO3
Answer:
(a) Conc. HNO3
II. Fill in the blanks.
Question 1.
Matte is a mixture of ______.
Answer:
Cu2S + FeS.
Question 2.
Second group elements are called ______.
Answer:
Alkaline earth metals.
Question 3.
Ionisation energy is measured in _____ unit.
Answer:
kJ/mol

Question 4.
The ionisation energy ______ along the period.
Answer:
Increases.
Question 5.
______ property, which predicts the nature of bonding between the atoms in a molecule.
Answer:
Electronegativity.
Question 6.
If the difference in electronegativity between two elements is 1.7, the bond has ____ and _____.
Answer:
50% ionic character, 50% covalent character.
Question 7.
If the difference in electronegativity between two elements is less than 1.7, the bond is considered to be ______.
Answer:
Covalent.
Question 8.
If the difference in electronegativity between two elements is greater than 1.7, the bond is considered to be ______.
Answer:
Ionic.
Question 9.
The process of extracting the ores from the earth’s crust is called ______.
Answer:
Mining.
Question 10.
______ is the main principle behind in Hydraulic method.
Answer:
Specific gravity.
Question 11.
Froth floatation process is preferable for ______ ores.
Answer:
Lighter
(or)
Sulphide.

Question 12.
On heating in air, iron forms ______.
Answer:
Fe3O4
Question 13.
Iron reacts with Chlorine to form _____ compound.
Answer:
Ferric chloride.
Question 14.
The corrosive action in the absence of moisture is called ______.
Answer:
Dry corrosion.
Question 15.
______ technique used to renovate the Pamban bridge.
Answer:
Protective coating.
Question 16.
The atomic number is the number of ____ in the nucleus or number of ______ revolving around the nucleus in an atom.
Answer:
Protons, electrons.
Question 17.
The long form of periodic table is based upon the _____ of elements.
Answer:
Electronic configuration.
Question 18.
In the periodic table, the horizontal rows are called _____ and vertical columns are called ______.
Answer:
Periods, groups.
Question 19.
The modem periodic table has been divided into ______ blocks known as _______ blocks.
Answer:
Four, s, p, d, f
Question 20.
The ______ of the elements in a period decreases from left to right and the atomic radii of the elements present in a group downwards.
Answer:
Atomic size, increases.
Question 21.
_______ period is the longest period and it contains ______ elements.
Answer:
Seventh, 32.
Question 22.
In the periodic table, there are ______ groups and _____ periods.
Answer:
18, 7.
Question 23.
Metals like Ti, Cr, Mn, Zr find their application in the manufacturing of defence equipment called ______.
Answer:
Strategic metals.
Question 24.
The metal ______ plays a vital role in nuclear reactions releasing nuclear energy and used in nuclear weapons.
Answer:
Uranium.
Question 25.
Copper, silver and gold are called _______ as they are used in making ____ and ______.
Answer:
Coinage metals, coins and jewellery.

Question 26.
Purity of gold is expressed in ______ and ______ is pure gold.
Answer:
Carats, 24 – carat gold.
Question 27.
_______ is an ore of aluminium and _____ is its mineral.
Answer:
Bauxite, clay.
Question 28.
All ______ cannot be called as ores but all ______ are minerals.
Answer:
Minerals, ores.
Question 29.
The process of extracting the ores from the earth’s crust is called ______.
Answer:
Mining.
Question 30.
The rocky impurity associated with the ore is called ____ or ______.
Answer:
Gangue, matrix.
Question 31.
_____ is a substance added to the ore to reduce the fusion temperature and to remove impurities.
Answer:
Flux.
Question 32.
____ is the process of reducing the roasted metallic oxide to metal.
Answer:
Smelting.
Question 33.
Slag is the fusible product formed when ____ reacts with ____ during the extraction of metals.
Answer:
Flux, gangue
Question 34.
The temperature applied in Hall’s process is _____ and the voltage used in ______.
Answer:
900 – 950°C, 5 – 6V
Question 35.
_____ is used in making manhole covers and drain pipes and _______ is used in making transmission cables and T.V. towers.
Answer:
Pig iron, steel.
Question 36.
______ is defined as the slow and steady destruction of a metal by the environment.
Answer:
Corrosion.
Question 37.
_______ is a process of coating zinc on iron sheets by using electric current.
Answer:
Galvanization.
III. Match the following.
Question 1.
| i. Boron family |
(a) Group 17 |
| ii. Carbon family |
(b) Group 16 |
| iii. Nitrogen family |
(c) Group 13 |
| iv. Chalcogen family |
(d) Group 15 |
| v. Halogen family |
(e) Group 14 |
Answer:
i – c, ii – e, iii – d, iv – b , v – a.
Question 2.
| i. Alkali metals |
(a) Lanthanides & Actinides |
| ii. Alkaline earth metals |
(b) Groups 3 – 12 |
| iii. Transition elements |
(c) Group 2 |
| iv. Inner transition elements |
(d) Group 1 |
Answer:
i – d, ii – c, iii – b, iv – a.
Question 3.
| i. Group 18 |
(a) Main group elements |
| ii. Group 3 – 12 |
(b) Noble gases |
| iii. Group 13 – 18 |
(c) Halogens |
| iv. Group 17 |
(d) Transition elements |
Answer:
i – b, ii – d, iii – a, iv – c.
Question 4.
| i. Copper |
(a) Lustrous greyish white metal |
| ii. Iron |
(b) Cn 112 |
| iii. Aluminium |
(c) Reddish-brown metal |
| iv. Copernicium |
(d) Silvery white metal |
Answer:
i – c, ii – a, iii – d, iv – b.
Question 5.
| Alloys |
Composition |
| i. Brass |
(a) Al, Mg, Mn, Cu |
| ii. Duralumin |
(b) Cu, Zn |
| iii. Bronze |
(c) Al, Mg |
| iv. Magnalium |
(d) Cu, Sn |
Answer:
i – b, ii – a, iii – d, iv – c.
Question 6.
| Elements |
Electronegative value |
| i. F |
(a) 2.5 |
| ii. Cl |
(b) 2.8 |
| iii. Br |
(c) 3.0 |
| iv. I |
(d) 4.0 |
Answer:
i – d, ii – c, iii – b, iv – a.
Question 7.
| Process |
Ores |
| i. Hydraulic process |
(a) ZnS |
| ii. Magnetic separation |
(b) Fe2O3 |
| iii. Froth floatation process |
(c) SnO2 |
| iv. Leaching process |
(d) Al2O3. 2H2O |
Answer:
i – b, ii – c, iii – a, iv – d.
Question 8.
| i. Cuprite |
(a) Halide ore |
| ii. Marble |
(b) Oxide ore |
| iii. Fluorspar |
(c) Sulphide ore |
| iv. Galena |
(d) Carbonate ore |
Answer:
i – b, ii – d, iii – a, iv – c.
Question 9.
| Alloy |
Metals present |
Uses |
| 1. Brass |
Fe, C, Ni |
Statues, Coins |
| 2. Bronze |
Al, Mg, Mn, Cu |
Aircraft, Pressure cookers |
| 3. Duralumin |
Fe, C, Ni, Cr |
Cables, Propeller |
| 4. Magnalium |
Cu, Sn |
Automobile parts, Utensils |
| 5. Stainless steel |
Cu, Zn |
Scientific instruments, Air craft |
| 6. Nickel steel |
Al, Mg |
Medals, decorative items |
Answer:
| Alloy |
Metals present |
Uses |
| 1. Brass |
Cu, Zn |
Medals, decorative items |
| 2. Bronze |
Cu, Sn |
Statues, Coins |
| 3. Duralumin |
Al, Mg, Mn, Cu |
Aircraft, Pressure cookers |
| 4. Magnalium |
Al, Mg |
Scientific instruments, Air craft |
| 5. Stainless steel |
Fe, C, Ni, Cr |
Automobile parts, Utensils |
| 6. Nickel steel |
Fe, C, Ni |
Cables, Propeller |
Question 10.
| Metal |
Ore |
Chemical formula |
| 1. Copper |
Bauxite |
ZnCO3 |
| 2. Aluminium |
Haematite |
CuFeS2 |
| 3. Iron |
Copper pyrite |
Fe2O3 |
| 4. Zinc |
Calamine |
Al2O3.2H2O |
Answer:
| Metal |
Ore |
Chemical formula |
| 1. Copper |
Copper pyrite |
CuFeS2 |
| 2. Aluminium |
Bauxite |
Al2O3.2H2O |
| 3. Iron |
Haematite |
Fe2O3 |
| 4. Zinc |
Calamine |
ZnCO3 |
IV. State whether true or false. If false, give the correct statement.
Question 1.
First period contains only one element.
Answer:
False.
Correct Statement: First period contains two elements.(Hydrogen & Ftelium)
Question 2.
The valency of all alkali metals is one.
Answer:
True.

Question 3.
Noble gases are more reactive.
Answer:
False.
Correct Statement: Noble gases are less reactive.
Question 4.
The atomic radius decreases from Li to B?
Answer:
True.
Question 5.
As the positive charge increases, the size of the cation also increases.
Answer:
False.
Correct Statement: As the positive charge increases, the size of the cation also decreases.
Question 6.
Copper pyrite ore is concentrated by gravity separation method.
False
Correct Statement: Copper pyrite ore is concentrated by froth floatation process.
Question 7.
Aluminium alloyed with gold and silver for making coins and jewels.
Answer:
False.
Correct Statement: Copper alloyed with gold and silver for making coins and jewels.
Question 8.
The corrosive action in the presence of moisture is called wet corrosion.
Answer:
True
Question 9.
The physical and chemical properties of elements are the periodic function of their atomic numbers – modern periodic law.
Answer:
True.
Question 10.
The long form of periodic table consists of horizontal rows called groups and vertical columns called periods.
Answer:
False.
Correct statement: The long form of periodic table consists of horizontal rows called periods and vertical columns called groups.
Question 11.
The first period in the periodic table is the shortest period and contains 8 elements from Lithium to Neon.
Answer:
False.
Correct statement: The first period in the periodic table is the shortest period and contains 2 elements Hydrogen and Helium.
(OR)
The second period in the periodic table is the short period and contains 8 elements from Lithium to Neon.
Question 12.
The sixth period in the periodic table is the longest period and contains 32 elements.
Answer:
True.
Question 13.
Group 1, 2 and 13 – 18 are called normal elements.
(or)
Main group elements.
(or)
Representative elements.
Answer:
True.
Question 14.
The atomic size of the elements in a period increases from left to right.
Answer:
False.
Correct statement: The atomic size of the elements in a period decreases from left to right.
Question 15.
In a period, the metallic character of the element increases while their non-metallic character decreases.
Answer:
False.
Correct statement: In a period, the metallic character of the element decreases while their non-metallic character increases.

Question 16.
The last element authenticated by IUPAC is Cn 112 [Copemicium].
Answer:
True.
Question 17.
Silver was the first metal to be used in making utensils and weapons.
Answer:
False.
Correct statement: Copper was the first metal to be used in making utensils and weapons.
Question 18.
The strategic metals such as copper, silver and gold are used in the manufacturing of defence equipment.
Answer:
False.
Correct statement: The strategic metals such as titanium, chromium manganese, zirconium are used in the manufacturing of defence equipment.
Question 19.
Copper, silver and gold are called coinage metals.
Answer:
True.
Question 20.
For making ornaments, 24 – carat gold is used which is pure gold.
Answer:
False.
Correct statement: For making ornaments, 22 – carat gold is used which contains 22 parts of gold by weight and 2 parts of copper by weight.
Question 21.
The mineral from which a metal can be readily and economically extracted on a large scale is said to be ore.
Answer:
True.
Question 22.
The rocky impurity associated with the ore is called flux.
Answer:
False.
Correct statement: The rocky impurity associated with the ore is called gangue or matrix.
Question 23.
Slag is the fusible product formed when flux reacts with gangue during the extraction of metals.
Answer:
True.
Question 24.
Metals which have high chemical reactivity are found in a free state or in the native state.
Answer:
False.
Correct statement: Metals which have low chemical reactivity are found in a free state or in the native state.
Question 25.
Aluminium is the metal found most abundantly in the earth’s crust.
Answer:
True
Question 26.
Aluminium is a reddish-brown metal and it is a bad conductor of heat and electricity.
Answer:
False.
Correct statement: Aluminium is a silvery – white metal and it is a good conductor of heat and electricity.

Question 27.
Aluminium reacts with strong caustic alkalis forming aluminates.
Answer:
True
Question 28.
Conc. Nitric acid renders aluminium active due to the formation of nitride film on its surface.
Answer:
False.
Correct statement: Cone. Nitric acid renders aluminium passive due to the formation of oxide film on its surface.
Question 29.
Aluminium is a powerful reducing agent.
Answer:
True.
Question 30.
Duralumin alloy is light, having high tensile strength and corrosion-resistant.
Answer:
True.
Question 31.
Fe and Al2O3 are used in thermite welding.
Answer:
False.
Correct statement: Al powder and Fe2O3 is used in thermite welding.
Question 32.
The chief ore of copper is Ruby copper.
Answer:
False.
Correct statement: The chief ore of copper is copper pyrite.
Question 33.
Iron is a lustrous greyish white metal and can be magnetised.
Answer:
True.
Question 34.
The rust has the chemical formula as Fe3O4.
Answer:
False.
Correct statement: The rust has the chemical formula as Fe2O3. xH2O.
V. Assertion and Reason.
Question 1.
Assertion (A): Nobel gas is unreactive.
Reason (R): They have unstable electronic configuration in their valence shells.
(a) Both (A) and (R) are correct
(b) Both (A) and (R) are not correct
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(c) (A) is correct but (R) is wrong
Question 2.
Assertion (A): The nature of bond in NaI molecule is covalent.
Reason (R): The electronegativity difference between Na and I is 1.5
(a) Both (A) and (R) are correct
(b) Both (A) and (R) are not correct
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct
Question 3.
Assertion (A): Haematite ore was purified by Hydraulic method.
Reason (R): Haematite is oxide ore.
(a) Both (A) and (R) are correct
(b) Both (A) and (R) are wrong
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct

Question 4.
Assertion (A): Corundum is a chief ore of aluminium.
Reason (R): Molecular formula of Corundum is Al2O3
(a) (A) and (R) are correct, (R) explains the (A)
(b) (A) is correct, (R) is wrong
(c) (A) is wrong, (R) is correct
(d) (A) and (R) are correct, (R) doesn’t explain (A).
Answer:
(c) (A) is wrong, (R) is correct
Question 5.
Assertion (A): The chemical properties of the elements in the same period are not similar.
Reason (R): As the electronic configuration changes across the period, the chemical properties of the elements are not similar.
(a) Both (A) and (R) are correct
(b) Both (A) and (R) are not correct
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct
Question 6.
Assertion (A): Copper, Silver and Gold are used in making coins and jewellery. So they are called coinage metals.
Reason (R): These metals release an enormous amount of nuclear energy.
(a) Both (A) and (R) are correct
(b) Both (A) and (R) are wrong
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(c) (A) is correct but (R) is wrong
Question 7.
Assertion (A): Metals like Titanium, Chromium, Manganese and Zirconium are called strategic metals!
Reason (R): They find their applications in the manufacturing of defence equipment.
(a) Both (A) and (R) are correct
(b) Both (A) and (R) are wrong
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct
Question 8.
Assertion (A): Gold, Silver and Platinum are the metals that are found in a free state.
Reason (R): Those metals have low chemical reactivity and are found in a free state or in the native state.
(a) Both (A) and (R) are wrong
(b) Both (A) and (R) are correct
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(b) Both (A) and (R) are correct
Question 9.
Assertion (A): Aluminium occurs in the combined state.
Reason (R): It is a reactive metal and so it occurs in combined state.
(a) Both (A) and (R) are correct
(b) Both (A) and (R) are wrong
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct
Question 10.
Assertion (A): In the aluminothermic process, Iron oxide is reduced to iron by igniting with Aluminium powder.
Reason (R): Aluminium is a powerful reducing agent.
(a) Both (A) and (R) are wrong
(b) (A) is correct but (R) is wrong
(c) (A) is wrong but (R) is correct
(d) Both (A) and (R) are correct.
Answer:
(d) Both (A) and (R) are correct
Question 11.
Assertion (A): When iron is dipped in conc.HNO3 it becomes chemically inert (or) passive.
Reason (R): Iron becomes passive when treated with nitric acid is due to the formation of a layer of iron oxide Fe3O4 on its surface.
(a) Both (A) and (R) are correct
(b) (A) is correct but (R) is wrong
(c) (A) is wrong but (R) is correct
(d) Both (A) and (R) are wrong.
Answer:
(d) Both (A) and (R) are wrong
Question 12.
Assertion (A): Duralumin is used in making aircraft, tools and pressure cookers.
Reason (R): Duralumin is an alloy that is light, strong, resistant to corrosion.
(a) Both (A) and (R) are wrong
(b) Both (A) and (R) are correct
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(b) Both (A) and (R) are correct
Question 13.
Assertion (A): Nickel steel is used in making cables, aircraft parts and propeller.
Reason (R): Nickel steel alloy is hard, brittle and polishable.
(a) Both (A) and (R) are correct
(b) Both (A) and (R) are wrong
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(c) (A) is correct but (R) is wrong
Question 14.
Assertion (A): Magnesium is used in a sacrificial protection method to prevent corrosion.
Reason (R): Magnesium is more reactive than iron. When it is coated on the articles made of steel, it sacrifices itself to protect steel.
(a) Both (A) and (R) are correct
(b) Both (A) and (R) are wrong
(c) (A) is correct but (R) is wrong
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct
Question 15.
Assertion (A): Electroplating method not only protects but also enhances the metallic appearance.
Reason (R): Electroplating is a method of coating one metal with another by passing current.
(a) (A) is right, (R) is wrong
(b) (A) is right, (R) is not relevant
(c) (A) is right, (R) is relevant
(d) Both (A) and (R) are wrong.
Answer:
(c) (A) is right, (R) is relevant
VI. Short Answer Questions.
Question 1.
State modern periodic law.
Answer:
Modem periodic law states that the physical and chemical properties of elements are the periodic function of their atomic numbers.
Question 2.
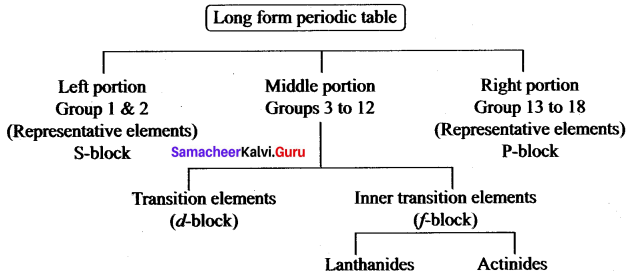
Write the flow chart of the long form of the periodic table.
Answer:
Question 3.
The distance between the adjacent copper atoms in solid copper is 2.56 Å. Calculate what is the metallic radius of Cu?
Answer:
Metallic radius of copper = \(\frac{2.56}{2}\) = 1.28 Å
Question 4.
Briefly write any four characteristics of a group in the periodic table.
Answer:
- The elements present in a group have the same valency.
- The elements present in a group have identical chemical properties.
- The physical properties of the elements in the group very gradually.
- The atomic radii of die elements present in a group increase downwards.
Question 5.
What is the principle behind Froth floatation?
Answer:
This process depends on the preferential wettability of the ore with oil (pine oil) and the gangue particles by water. Lighter ores, such as sulphide ores, are concentrated by this method. Eg: Zinc blende (ZnS).
Question 6.
What are minerals?
Answer:
A mineral may be a single compound or a complex mixture of various compounds of metals found in the earth, e.g. Clay Al2O3. 2SiO2. 2H2O is the mineral of Aluminium.
Question 7.
Write the increasing order of radii of the following species.
(a) Na, Na+, Cl, Cl–
(b) Li, Na, K, Rb
Answer:
(a) Na+, Cl, Na, Cl–
(b) Li, Na, K, Rb
Question 8.
Differentiate ore and mineral.
Answer:
| Ore |
Mineral |
| 1. Ores contain a large percentage of metal. |
1. Minerals contain a low percentage of metal. |
| 2. Ores can be used for die extraction of metals on a large scale readily and economically. |
2. Metals cannot be extracted easily from minerals. |
| 3. Bauxite Al2O3. 2H2O is the ore of aluminium. |
3. Clay Al2O3.2SiO.2H2O is the mineral of aluminium. |
Question 9.
Define metallurgy.
Answer:
The various steps involved in the extraction of metals from their ores as well as refining of crude metals are collectively known as metallurgy.
Question 10.
Elements a, b, c and d have the following electronic configurations
(a) ls2 2s² 2p6
(b) Is², 2s², 2p6, 3s², 3p1
(c) Is², 2s², 2p6, 3s², 3p6
(d) Is², 2s², Ip1
Answer:
(a) and (c), (b) and (d). Because the number of valence electrons are the same.
Question 11.
What is slag? Give an example.
Answer:
Slag is a fusible product formed when flux reacts with gangue during the extraction of metals.
Flux + gangue → slag
CaO + SiO2 → CaSiO3
Question 12.
Why the electron affinities of noble gases are zero?
Answer:
Noble gases show no tendency to accept electrons because the outer 5 and p orbitals of noble gases are completely filled. No more electrons can be added to them and hence their electron affinities are zero.
Question 13.
Why does gold, silver and platinum occur in free state?
Answer:
Gold, silver and platinum have low chemical reactivity and so they are found in the free state or in a native state.
Question 14.
How does Aluminium reacts with air?
Answer:
Reaction with air: It is not affected by dry air. On heating at 800°C, aluminium bums very brightly forming it’s oxide and nitride.
4Al + 3O2 → Al2O3(Aluminium oxide)
2Al + N2 → 2 AlN (Aluminium nitride)
Question 15.
How does Aluminium react with caustic soda? Give an equation.
Answer:
Aluminium reacts with caustic soda to give sodium meta aluminate with the liberation of H2 gas.
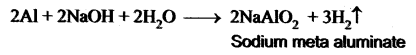
Question 16.
Prove that aluminium is a powerful reducing agent.
Answer:
Aluminium is a powerful reducing agent When a mixture of aluminium powder and iron oxide is ignited, iron oxide is reduced to iron. This process is known as the aluminothermic process.
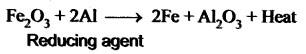
Question 17.
Write a note on Aluminothermic process.
Answer:
As reducing agent: Aluminium is a powerful reducing agent. When a mixture of aluminium powder and iron oxide is ignited, the latter is reduced to metal. This process is known as aluminothermic process.
Fe2O3 + 2Al → 2Fe + Al2O3 + heat
Question 18.
What is the action of heat on copper?
Answer:
On heating at different temperatures in the presence of oxygen, copper forms two types of oxides CuO, Cu2O.

Question 19.
Explain the action of dilute nitric acid with copper.
Answer:
Copper reacts with dil.HNO3 with the liberation of Nitric oxide gas.
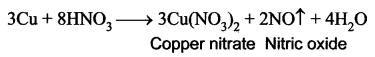
Question 20.
What happens when copper is treated with conc.HNO3 and with conc.H2SO4?
Answer:

Question 21.
What do you mean by Ferrous and Non-Ferrous alloys? Given an example for each.
Answer:
Ferrous alloys : Contain iron as a major component.
Eg: Stainless steel, Nickel steel
Non-Ferrous alloys : These alloys do not contain iron as a major part.
Eg: Aluminium alloy, Copper alloy.
Question 22.
Explain the action of air with iron.
Answer:
3Fe + 2O2 → Fe3O4 [Magnetic oxide (Black)].
Question 23.
What are amalgams? How are they prepared?
Answer:
An amalgam is an alloy of mercury with another metal.
Amalgams are formed by the metallic bonding with the electrostatic force of attraction between the electrons and the positively charged metal ions.
Question 24.
Explain the action of steam with iron.
Answer:

Question 25.
Mention the types of iron on the basis of carbon content.
Answer:
| Pig iron |
Iron with 2 – 4.5% carbon |
| Wrought iron |
Iron with < 0.25% carbon |
| Steel |
Iron with 0.25 – 2% carbon |
Question 26.
What is dry corrosion or chemical corrosion?
Answer:
The corrosive action in the absence of moisture is called dry corrosion. It is the process of a chemical attack on a metal by corrosive liquids or gases such as O2, N2, SO2, H2S etc… It occurs at high temperature, of all the gases mentioned above O2 is the most reactive gas to impart the chemical attack.
Question 27.
What is an amalgam? Give one example with its use.
Answer:
- An amalgam is an alloy of mercury with metals such as sodium, gold and silver.
- Dental amalgam is an alloy of mercury with silver and tin and it is used in the dental filling.
Question 28.
Explain sacrificial protection.
Answer:
Magnesium is more reactive than iron. When it is coated on the articles made of steel, it sacrifices itself to protect steel.
Question 29.
Define corrosion.
Answer:
Corrosion is defined as the slow and steady destruction of a metal by the environment. It results in the deterioration of the metal to form metal compounds by means of chemical reactions with the environment.
Question 30.
What is the action of Air and moisture on copper?
Answer:
Copper gets covered with a green layer of basic carbonate in the presence of CO2 and moisture.
2 Cu + O2 + CO2 + H2O → CUCO3.CU(OH)2
Question 31.
Give any two uses of aluminium.
Answer:
- Aluminium metal is a corrosion – resistant and a good conductor of heat. So it is used in making utensils.
- Aluminium is used in welding as thermite and a very good reducing agent.
Question 32.
What is the modern periodic table?
Answer:
The modem periodic table is a tabular arrangement of elements in rows and columns, highlighting the regular repetition of properties of the elements.
Question 33.
Explain the smelting process of iron in the Blast furnace.
Answer:
The charge consisting of roasted ore, coke and limestone in the ratio 8 : 4 : 1 is smelted in a blast furnace by introducing it through the cup and cone arrangement at the top.
Question 34.
What are the periodic properties?
Answer:
Properties such as atomic radius, ionic radius, ionisation energy, electronegativity, electron affinity, show a regular periodicity and hence they are called periodic properties.
Question 35.
Define Atomic radius.
Answer:
The atomic radius of an atom is defined as the distance between the centre of its nucleus and the outermost shell containing the valence electron.
Question 36.
Write the action of dil.HCl and dil.H2SO4 with iron.
Answer:
(i) Fe + 2HCl → FeCl2 + H2↑
(ii) Fe + H2SO4 → FeSO4 + H2↑
Question 37.
What is a covalent radius?
Answer:
It is defined as half the distance between the nuclei of two covalently bonded atoms of the same element in a molecule.
Question 38.
Define Ionisation energy.
Answer:
Ionisation energy is the minimum energy required to remove an electron from a gaseous atom in its ground state to form a cation.
Question 39.
What is an alloy?
Answer:
An alloy is a homogeneous mixture of two or more metals or of one or more metals with certain non-metallic elements. The properties of alloys are often different from the component metals.

Question 40.
What is Electronegativity?
Answer:
Electronegativity of an element is the measure of the tendency of its atom to attract the shared pair of electrons towards itself in a covalent bond.
Question 41.
Write the steps involved in metallurgical process.
Answer:
A metallurgical process involves three main steps as follows:
- Concentration or Separation of the ore: It is the process of removal of impurities from the ore.
- Production of the metal: It is the conversion of the ore into metal.
- Refining of the metal: It is the process of purification of the metal.
Question 42.
Give a single term for each of the following:
(i) The process of extracting the ores from the Earth’s crust is called:
Answer:
Mining
(ii) The rocky impurities associated with an ore is called:
Answer:
Gangue or matrix
(iii) The substance added to the ore to reduce fusion temperature:
Answer:
Flux
(iv) Noble metals occur in this state:
Answer:
Native
Question 43.
How will you convert copper into copper carbonate?
Answer:
Copper reacts with oxygen in the presence of CO2 and moisture to give copper carbonate.
2Cu + O2 + CO2 + H2O → CuCO3. Cu(OH)2 (Copper Carbonate).
Question 44.
Mention the uses of iron.
Answer:
Uses of iron:
- Pig iron (Iron with 2 – 4.5 % of carbon): It is used in making pipes, stoves, radiators, railings, manhole covers and drain pipes.
- Steel (Iron with < 0.25 % of carbon): It is used in the construction of buildings, machinery, transmission cables and T.V towers and in making alloys.
- Wrought iron (Iron with 0.25 – 2 % of wrought carbon): It is used in making springs, anchors and electromagnets.
Question 45.
What are the chemical properties of metals in terms of
- valence electrons
- Atomicity.
Answer:
- Valence electrons: Metals usually have 1, 2 or 3 electrons in their outermost shell.
- Atomicity: Metals are usually monoatomic in their vapour state.
Question 46.
Why alloys are said to solid solutions?
Answer:
Alloys can be considered solid solutions in which the metal with high concentration is solvent and other metals are solute.
Example: brass is a solid solution of zinc (solute) in copper (solvent).
Question 47.
Write a note on Dry corrosion.
Answer:
- The corrosive action in the absence of moisture is called dry corrosion.
- It is the process of a chemical attack on a metal by corrosive liquids or gases such as O2, N2, SO2, H2S etc. in which O2 is more reactive.
- It occurs at high temperature
Question 48.
Explain Wet Corrosion.
Answer:
- The corrosive action in the presence of moisture is called wet corrosion.
- It occurs as a result of the electrochemical reaction of metal with water or an aqueous solution of salt or acids or bases.
Question 49.
What is electroplating?
Answer:
Electroplating is a method of coating one metal over another metal by passing an electric current.
VII. Long Answer Questions.
Question 1.
Explain the variation of ionisation energy along the group and period.
Answer:
- As the atomic size decreases from left to right in a period, more energy is required to remove the electrons. So, the ionisation energy increases throughout the period.
- Down the group, the atomic size increases and hence the valence electrons are loosely bound. They require relatively less energy for the removal. Thus, ionisation energy decreases down the group in the periodic table.
Question 2.
Explain the electrolytic refining of copper.
Answer:
(i) Blister copper contains 98% of pure Cu and 2 % of impurities and is purified by electrolytic refining.
For electrolytic refining of Cu we use:
Cathode: A thin plate of pure Cu.
Anode: A block of impure Cu
Electrolyte: CuSO4 + dil H2SO4
(ii) When electric current is passed through the electrolytic solution, Pure Cu gets deposited at the cathode and the impurities settle at the bottom of the anode in the form of anode mud.
Question 3.
Explain Gravity separation method.
Answer:
Gravity Separation (or) Hydraulic method:
1. Principle: The difference in the densities or specific gravities of the ore and the gangue is the main principle behind this method. Oxide ores are purified by this method,
e.g., Haematite Fe2O3 the ore of iron.
2. Method: The ore is poured over a sloping, vibrating corrugated table with grooves and a jet of water is allowed to flow over it. The denser ore particles settle down in the grooves and lighter gangue particles are washed down by the water.
Question 4.
Discuss the magnetic separation methods.
Answer:
Magnetic separation method:
Principle: The magnetic properties of the ores from the basis of separation. When either the ore or the gangue is magnetic, this method is employed, e.g., Tinstone SnO2, the ore of tin.
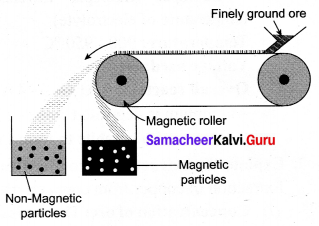
Method: The crushed ore is placed over a conveyer belt which rotates around two metal wheels, one of which is magnetic. The magnetic particles are attracted to the magnetic wheel and fall separately apart from the nonmagnetic particles.
Question 5.
Explain the froth floatation process.
Answer:
Froth floatation Process:
Principle: This process depends on the preferential wettability of the ore with oil (pine oil) and the gangue particles by water. Lighter ores, such as sulphide ores, are concentrated by this method, e.g., Zinc blende (ZnS).
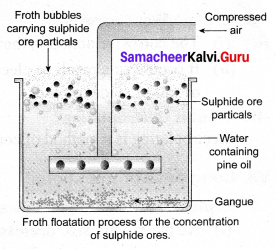
Method: The crushed ore is taken in a large tank containing oil and water and agitated with a current of compressed air. The ore is wetted by the oil and gets separated from the gangue in the form of froth. Since the ore is lighter, it comes on the surface with the froth and the impurities are left behind, e.g., Zinc blende (ZnS).
Question 6.
How will you extract aluminium from its ore?
Answer:
The extraction of aluminium from bauxite involves two steps:
(i) Conversion of bauxite into alumina – Baeyer’s Process
The conversion of Bauxite into Alumina involves the following steps:
Bauxite ore is finely ground and heated under pressure with a solution of concentrated caustic soda solution at 150° C to obtain sodium metal aluminate.
On diluting sodium meta aluminate with water, a precipitate of aluminium hydroxide is formed.
The precipitate is filtered, washed, dried and ignited at 1000°C to get alumina.
\(2 \mathrm{Al}(\mathrm{OH})_{3} \stackrel{1000^{\circ} \mathrm{C}}{\longrightarrow} \mathrm{Al}_{2} \mathrm{O}_{3}+3 \mathrm{H}_{2} \mathrm{O}\)
(ii) Electrolytic reduction of alumina – Hall’s Process
Aluminium is produced by the electrolytic reduction of fused alumina (Al2O3) in the electrolytic cell.
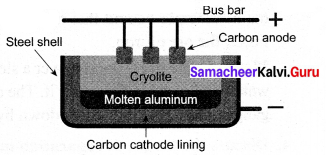
Cathode: Iron tank linked with graphite
Anode: A bunch of graphite rods suspended in a molten electrolyte.
Electrolyte: Pure alumina + molten cryolite + fluorspar (fluorspar lowers the fusion temperature of electrolyte)
Temperature: 900 – 950°C
The voltage used: 5 – 6 V
Aluminium is deposited at the cathode and oxygen gas is liberated at the anode. Oxygen combines with graphite to form CO2.
Question 7.
Explain the extraction of copper from copper pyrites.
Answer:
Extraction of copper from copper pyrites involves the following steps:
(i) The concentration of ore: The ore is crushed and then concentrated by froth floatation process.
(ii) Roasting: The concentrated ore is roasted in excess of air. During the process of roasting, the moisture and volatile impurities are removed. Sulphur, phosphorus, arsenic and antimony are removed as oxides. Copper pyrite is partly converted into sulphides of copper and iron.
\(2 \mathrm{CuFeS}_{2}+\mathrm{O}_{2} \rightarrow \mathrm{Cu}_{2} \mathrm{S}+2 \mathrm{FeS}+\mathrm{SO}_{2} \uparrow\)
(iii) Smelting: The roasted ore is mixed with powdered coke and sand and is heated in a blast furnace to obtain matte (Cu2S + FeS) and slag. The slag is removed as waste.
(iv) Bessemerisation: The molten matte is transferred to the Bessemer converter in order to obtain blister copper. Ferrous sulphide from matte is oxidized to ferrous oxide, which is removed as slag using silica.

(v) Refining: Blister copper contains 98% of pure copper and 2% of impurities and is purified A by electrolytic refining. This method is used to get metal of a high degree of purity. For electrolytic refining of copper, we use:
Cathode: A thin plate of pure copper metal.
Anode: A block of impure copper metal.
Electrolyte: Copper sulphate solution acidified with sulphuric acid.
When an electric current is passed through the electrolytic solution, pure copper gets deposited at the cathode and the impurities settle at the bottom of the anode in the form of sludge called anode mud.
Question 8.
Explain the metallurgy of iron.
Answer:
Iron is chiefly extracted from haematite ore (Fe2O3):
(i) Concentration by Gravity Separation: The powdered ore is washed with steam of water. As a result, the lighter sand particles and other impurities are washed away and the heavier ore particles settle down.
(ii) Roasting and Calcination: The concentrated ore is strongly heated in a limited supply of air in a reverberatory furnace. As a result, moisture is driven out and sulphur, arsenic and phosphorus impurities are oxidized off.
(iii) Smelting (in a Blast Furnace): The charge consisting of roasted ore, coke and limestone in the ratio 8 : 4 : 1 is smelted in a blast furnace by introducing it through the cup and cone arrangement at the top. There are three important regions in the furnace.
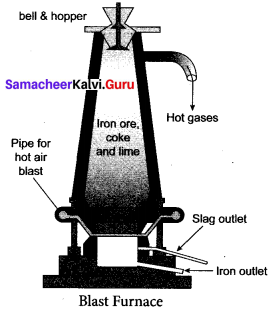
a. The Lower Region (Combustion Zone):
The temperature is at 1500°C. In this region, coke bums with oxygen to form CO2 when the charge comes in contact with a hot blast of air.
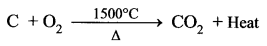
It is an exothermic reaction since heat is liberated.
b. The Middle Region (Fusion Zone):
The temperature prevails at 1000°C. In this region, CO2 is reduced to CO.
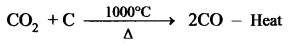
Limestone decomposes to calcium oxide and CO2
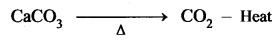
These two reactions are endothermic due to absorption of heat. Calcium oxide combines with silica to form calcium silicate slag.
CaO + SiO2 → CaSiO3
c. The Upper Region (Reduction Zone): The temperature prevails at 400°C. In this region carbon monoxide reduces ferric oxide to form a fairly pure spongy iron.
\(\mathrm{Fe}_{2} \mathrm{O}_{3}+3 \mathrm{CO} \stackrel{400^{\circ} \mathrm{C}}{\longrightarrow} 2 \mathrm{Fe}+3 \mathrm{CO}_{2}\)
The molten iron is collected at the bottom of the furnace after removing the slag.
The iron thus formed is called pig iron. It is remelted and cast into different moulds. This iron is called cast iron.
Question 9.
Explain the types of alloys.
Answer:
Based on the presence or absence of Iron, alloys can be classified into:
1. Ferrous alloys: Contain Iron as a major component.
A few examples of ferrous alloys are Stainless Steel, Nickel Steel etc.
2. Non – ferrous alloys: These alloys do not contain Iron as a major component.
For example, Aluminium alloy, Copper alloy etc.
Copper Alloys (Non – ferrous):
| Alloys |
Uses |
| Brass (Cu, Zn) |
Electrical fittings, medal, decorative items, hardware |
| Bronze (Cu, Sn) |
Statues, coins, bells, gongs |
Aluminium Alloys (Non – ferrous):
| Alloys |
Uses |
| Duralumin (Al, Mg, Mn, Cu) |
Aircraft tools, pressure cookers |
| Magnalium (Al, Mg) |
Aircraft, scientific instruments |
Iron Alloys(Ferrous):
| Alloys |
Uses |
| Stainless steel (Fe, C, Ni, Cr) |
Utensils, cutlery, automobile parts |
| Nickel steel (Fe, C, Ni) |
Cables, aircraft parts, propeller |
VIII. HOT Questions.
Question 1.
What would be the atomic number of the next
- alkali metal
- alkaline earth metal
- Halogens
- inert gas, if discovered in future.
Answer:
- Alkali metal: 118 + 1 = 119
- Alkaline earth metal: 120
- Halogens: 117
- Inert gas: 118
Question 2.
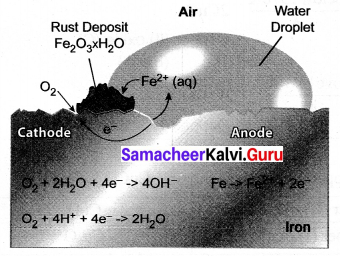
Explain the mechanism of rusting?
Answer:
Rust is chemically known as hydrated ferric oxide (it is formulated as Fe2O3.xH2O).
Rusting results in the formation of scaling reddish – brown hydrated ferric oxide on the surface of iron and iron-containing materials.
Question 3.
All ores are minerals, but ait minerals are not ores. Why?
Answer:
- The elements or compounds of the metals which occur in nature in the earth’s crust are called minerals whereas ore is a mineral from which the metal is profitably extracted.
- For example, aluminium exists in the two mineral forms, that is clay and bauxite. But aluminium is mainly extracted from bauxite which contains 70 % aluminium oxide. So, bauxite is an ore of aluminium whereas clay is not ore.
- So, all ores are minerals but all minerals need not be ores.
Question 4.
Why the graphite rods acting as anode in the Hall’s process should be replaced periodically?
Answer:
During Hall’s Process, the carbon electrodes get consumed, so they have to be replaced periodically.
Question 5.
Anionic radius Is higher than the corresponding neutral atom. Give reason.
Answer:
When an atom gains one or more electrons it forms an anion. During the formation of anion, the number of orbital electrons becomes greater than the nuclear charge. Hence, the electrons are not strongly attracted by the lesser number of nuclear charges. Hence anionic radius is higher than the corresponding neutral atom.
Question 6.
A reddish – brown metal A, when exposed to moist air, forms a green layer B. When A is heated at different temperatures in the presence of O2, it forms two types of oxides – C (black) and D (red). Identify A, B, C, D and write the balanced equation.
Answer:
(i) A reddish – brown metal A is a copper (Cu).
(ii) When copper (A) is exposed to moist air it forms a green layer (B) is copper carbonate.

(iii) When copper is heated at different temperature in the presence of oxygen, it forms two types of oxides CuO and Cu2O. (C and D)
Question 7.
A silvery – white metal on treatment with NaOH and HCl liberates H2 gas to form B and C respectively. The metal A will not react with acid D due to the formation of a passive film on the surface. Hence it is used for transporting acid D. Identify A, B, C, D and support your answer with balanced equations.
Answer:
(i) A silvery – white metal (A) is Aluminium (Al).
(ii) Aluminium reacts with NaOH to form B which is known as sodium meta aluminate with the liberation of H2 gas.

(iii) Aluminium reacts with HCl to form Aluminium chloride which is known as C with the liberation of H2 gas.

(iv) Aluminium does not react with conc. nitric acid (HNO3) which is known as D, due to the formation of a passive film on the surface.
| A |
Aluminium |
Al |
| B |
Sodium meta aluminate |
NaAlO2 |
| C |
Aluminium chloride |
AlCl3 |
| D |
Nitric acid |
HNO3 |
Question 8.
Metal A belongs to period 4 and group 8. A in red hot condition reacts with steam to form B. A reacts with dilute HNO3 to give C. A again reacts with conc. H2SO4 to give D. Find A, B, C and D with suitable reaction.
Answer:
(i) Metal (A) belongs to period 4 and group 8 is iron (Fe).
(ii) Iron (A) reacts with steam to form magnetic oxide (B)
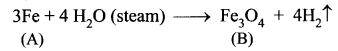
(iii) Iron (A) reacts with dilute HNO3 in cold condition to give ferrous nitrate (C).
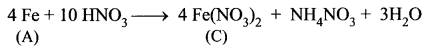
(iv) Iron (A) reacts with conc.H2SO4 to form Ferric Sulphate (D).


![]()





![]()
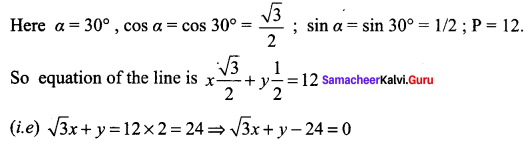
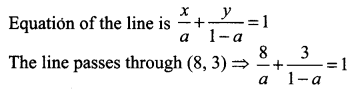
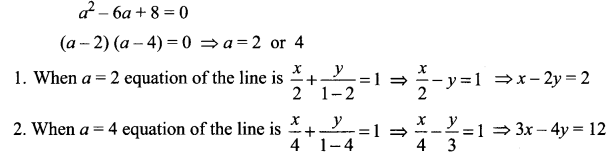

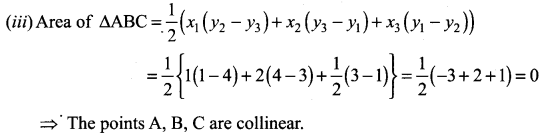

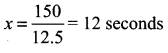
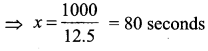
![]()




![]()

![]()
![]()
![]()

![]()