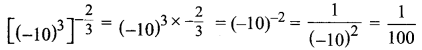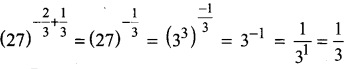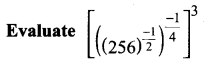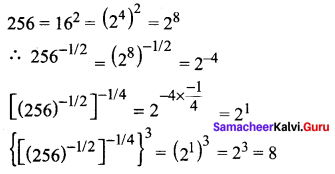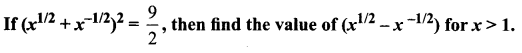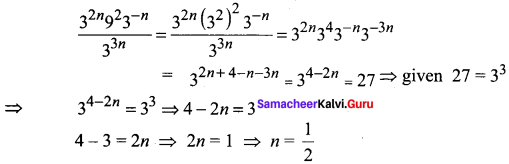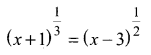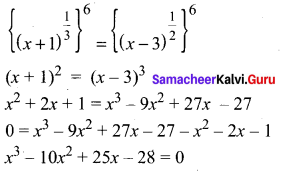Prasanna

Students can Download Chemistry Chapter 12 Basic Concepts of Organic Reactions Chemistry Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Chemistry Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Chemistry Solutions Chapter 12 Basic Concepts of Organic Reactions

Samacheer Kalvi 11th Chemistry Basic Concepts of Organic Reactions Textual Evaluation Solved

I. Choose The Best Answer:

Question 1.
For the Following reactions –
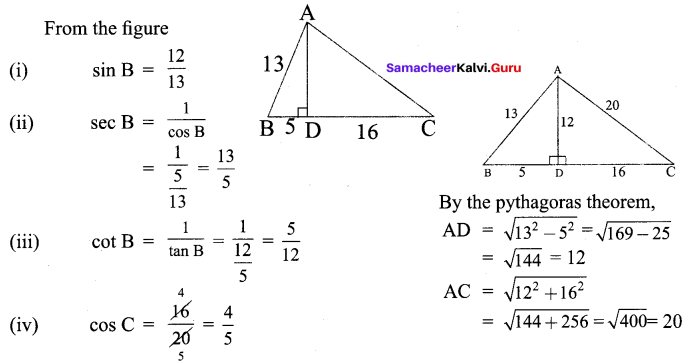
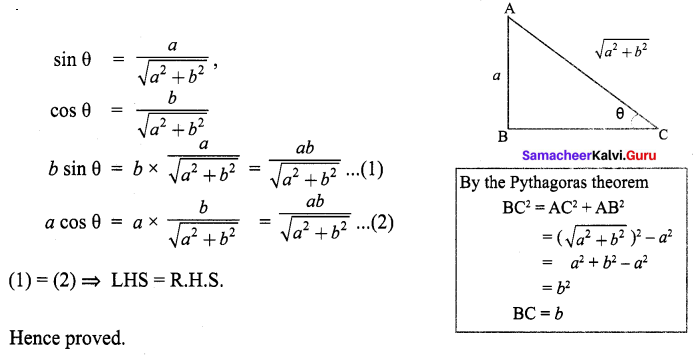
(A) CH₃ CH₂ CH₂ Br + KOH → CH₃ – CH + KBr + H₂O
(B) (CH₃ )₃ CBr + KOH → (CH₃ )₃ COH + KBr
(C)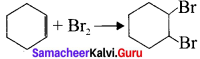
Which of the following statement is correct’?
(a) (A) is elimination, (B) and (C) are substitution
(b) (A) is substitution, (B) and (C) are elimination
(c) (A) and (B) are elimination and (C) is addition reaction
(d) (A) is elimination, B is substitution and (C) is addition reaction.
Answer:
(d) (A) is elimination, B is substitution and (C) is addition reaction.

Question 2.
What is the hybridisation state of benzyl carbonium ion?
(a) sp²
(b) spd²
(c) sp³
(d) sp²d
Answer:
(a) sp²

Question 3.
Decreasing order of nucleophilicity is –
(a) OH^–> RNH₂^– > ^–OCH₃> RNH₂
(b) NH₂^–> OH^–> ^–OCH₃> RNH₂
(c) NH,> CH₃O >OH^–> RNH₂
(d) CH₃O^–> NH₂^–> OH^–> RNH₂
Answer:
(b) NH₂^–> OH^–> ^–OCH₃> RNH₂₊

Question 4.
Which of the tòllowing species is not eLectrophilic in nature?
(a) Cl⁺
(b) BH₃
(c) H₃O⁺
(d) ⁺NO₂
Answer:
(c) H₃O⁺

Question 5.
Homolytic fission of covalent bond leads to the formation of –
(a) electrophile
(b) nucicophile
(c) Carbocation
(d) free radical
Answer:
(d) free radical

Question 6.
Hyper Conjugation is also known as –
(a) no bond resonance
(b) Baker – nathan effect
(c) both (a) and (b)
(d) none of these
Answer:
(c) both (a) and (b)

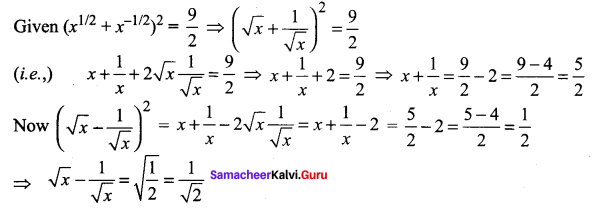
Question 7.
Which of the group has highest +I effect?
(a) CH₃^–
(b) CH₃CH₂^–
(c) (CH₃)₂ -CH-
(d) (CH₃)₃-C-
Answer:
(d) (CH₃)₃-C-

Question 8.
Which of the following species does not exert a resonance effect?
(a) C₆H₅OH
(b) C₆H₅Cl
(c) C₆H₅NH₂
(d) C₆H₅NH₃
Answer:
(d) C₆H₅NH₃

Question 9.
-I effect is shown by –
(a) -Cl
(b) -Br
(c) both (a) and (b)
(d) -CH₃
Answer:
(c) both (a) and (b)

Question 10.
Which of the following carbocation will be most stable?
(a) \({ PH }_{ 3 }\overset { + }{ C- } \)
(b) CH₃–\(\overset { + }{ C{ H }_{ 2 } } \)
(c) (CH₃)₂–\(\overset { + }{ C{ H } } \)
(d) CH₂ = CH-CH₃
Answer:
(a) \({ PH }_{ 3 }\overset { + }{ C- } \)

Question 11.
Assertion : Tertiary Carbocations are generally formed more easily than primary Carbocations.
Reason : Hyper conjugation as well as inductive effect due to additional alkyl group stabilize tertiary carbonium ions.
(a) both assertion and reason arc true and reason is the correct explanation of assertion.
(b) both assertion and reason are true but reason is not the correct explanation of assertion.
(c) Assertion is true but reason is false
(d) Both assertion and reason are false
Answer:
(a) both assertion and reason are true and reason is the correct explanation of assertion.

Question 12.
Heterolytic fission of C-C bond results in the formation of –
(a) free radical
(b) Carbanion
(c) Carbocation
(d) Carbanion and Carbocation
Answer:
(e) Carbocation

Question 13.
Which of the following represent a set of nucleophiles?
(a) BF₃, H₂O, NH^2-
(b) AlCl₃, BF₃, NH₃
(c) CN^–, RCH^–₂, ROH
(d) H⁺, RNH⁺₂, CCl₂
Answer:
(c) CN^–, RCH^–₂, ROH

Question 14.
Which of the following species does not acts as a nucleophile?
(a) ROH
(b) ROR
(c) PCl₃
(d) BF₃
Answer:
(d) BF₃

Question 15.
The geometrical shape of carbocation is
(a) Linear
(b) tetrahedral
(c) Planar
(d) Pyramidal
Answer:
(c) Planar

II. Write brief answer to the following questions.

Question 16.
Write short notes on:
(a) Resonance
(b) Hyper conjugation
Answer:
(a) Resonance:
1. Certain organic compounds can be represented by more than one structure and they differ only in the position of bonding and lone pair of electrons. Such structures are called resonance structure and this phenomenon is called as resonance. This phenomenon is also called as mesomerism or mesomeric effect.

2. For example, the structure of aromatic compounds such as benzene and conjugated system like 1,3 butadiene cannot be represent by a single structure and their observed properties can be explained on the base of a resonance hybrid.

3. Resonance structure of benzene.

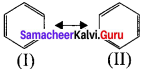
(I) and (II) are called as resonance hybridš of benzcnc.

4. For 1,3 butadiene:

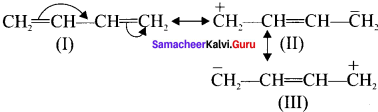
(I), (II) and (III) are called as resonance hybrids of 1,3 butadiene.

(b) Hyper conjugation:
1. The denationalization of electrons of σ bond is called as hyper conjugation. it is a special stabilizing effect that results due to the interaction of electrons of a σ bond with the adjacent empty non-bonding P-orbitais resulting in an extended molecular orbital.

2. Hyper conjugation is a permanent effect.

3. For example, in propane. the σ- electrons of C-H bond of methyl group can be delocalised into the it- orbital of doubly bonded carbon as represented below.

Question 17.
What are electrophiles and nucleophiles? Give suitable examples for each.
Answer:
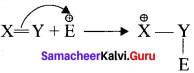
Nucleophiles are reagents that has high affinity for electron positive centers. They possess an atom that has an unshared pair of electrons, and hence it is in search for an electro-positive centre where it can have an opportunity to share its electrons to form a covalent bond, and gets stabilised. They are usually negatively charged ions or electron-rich neutral molecules (contains one or more lone pair of electrons). All Lewis bases act as nucleophiles.
Example :
Ammonia(NH₃) and amines (RNH₂), water (H₂O), alcohols (ROH) and ethers ((R-O-R)

Electrophiles:
Electrophiles are reagents that are attracted towards negative charge or electron-rich center. They are either positively charged ions or electron-deficient neutral molecules. All Lewis acids acts as electrophiles. Neutral molecules like SnCl4 can also act as an electrophile, as it has vacant d – orbitals which can accommodate the electrons from others.
Example:
Carbon dioxide (CO₂), dichlorocarbene (: CCl₂), Aluminium chloride (AlCl₃), boron trifluoride (BF₃) and Ferric Chloride (FeCl₃)

Question 18.
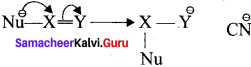
Show the heterolysis of the covalent bond by using curved arrow notation and complete the following equations. Identify the nucleophile In each case.
1. CH₃-Br+KOH →
2. CH₃-OCH₃+HI →
Answer:

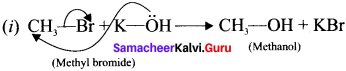
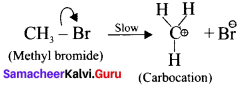
In this case, \(\overset { \ominus }{ Br } \) and \(\overset { \ominus }{ OH } \) are nucleophiles.

Another mechanism:
Step – I

Step-II

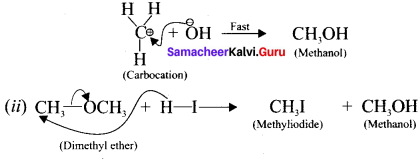
In this case, OCH₃ and -I are nucleophiles
Another mechanism:
Step – I

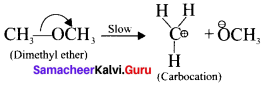
Step – II

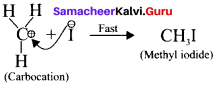
Question 19.
Explain inductive effect with suitable example.
Inductive effect:
Answer:
1. it is defined as the change ¡n the polarization of a covalent bond due to the presence of adjacent bonded atoms or groups in the molecule. It is denoted as I-effect.

2. Atoms or groups which lose electron towards a carbon atom are said to have a +I effect.
Example:
CH₃-,(CH₃)₂ CH-,(CH₃)₂ C- etc.

3. Atoms or groups which draw electrons away from a carbon atom are said to have a -I effect.
Example:
-NO₂. -I, -Br, -OH, C₆H₅ etc.

4. For example, consider ethane and ethyl chloride. The C-C bond in ethane is non polar while the C-C bond in ethyl chloride is polar. We know that chlorine is more electronegative than carbon and hence it attracts the shared pair of electrons between C-Cl in ethyl chloride towards it self.

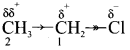
This develops a slight negative charge on chlorine and a slight positive charge on carbon to which chlorine is attached. To compensate it, the C₁ draws the shared pair of electron between itself and C₂. This polarization effect is called inductive effect.

Question 20.
Explain the electromeric effect.
Electromeric effect:
Answer:
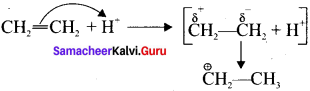
1. The electromeric effect refers to the polarity produced in a multiple bonded compound when it is attacked by a reagent when a double or a triple bond is exposed to an attack by an electrophile the two π electrons which from the π bond are completely transferred to one atom or the other.

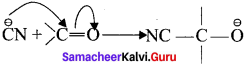
2. When a nucleophile approaches the carbonyl compound, the π-electrons between C and O is instantaneously shifted to the more electronegative oxygen. This makes the carbon electron-deficient and thus facilitating the formation of a new bond between the incoming nucleophile and the carbonyl carbon atom.

3. When an electrophile such as H approaches an alkene molecule their electrons are instantaneously shifted to the electrophile and a new bond is formed between carbon and hydrogen. This makes the other carbon electron-deficient and hence it acquires a positive charge.

4. This effect denotes as E-effect.

Question 21.
Give examples for the following types of organic reactions
1. – elimination
2. Electrophilic substitution.
Answer:
1. β-elimination:
Elimination reactions involve the cleavage of a bond and tórmation of an air bond. A nucleophilic pair of electrons heads into a new it bond as a leaving group departs. This process is called 3-elimination because the bond Í to the nucleophilic pair of electrons breaks.
Example:
(a) n-propyl bromide on reaction with alcoholic KOH give propene. in this reaction hydrogen and Br are eliminated.

(b) Acid-catalysed dehydration of alcohols

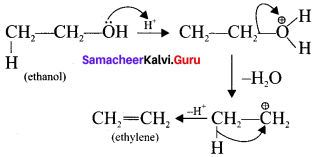
2. Electrophilic substitution:
Substitution reactions when are brought about by electrophiles are called electrophilic substitution reaction.
Example:
(a) Nitration of benzene

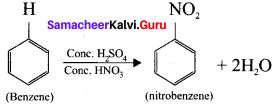
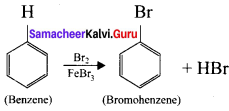
(b) Bromination of benzene:

Samacheer Kalvi 11th Chemistry Basic Concepts of Organic ReactionsAdditional Questions Solved

I. Choose The Correct Answer.

Question 1.
Statement-I: All the organic molecules contain covalent bonds.
Statement-II: Organic molecules are formed by the mutual sharing of electrons between atoms.
(a) Statement-I and II are correct and statement-II is the correct explanation of statement-I.
(b) Statement-I and II are correct but Statement-II is not the correct explanation of statement-I.
(c) Statement-I is correct but statement-II is wrong.
(d) Statement-I is wrong but statement-II is correct.
Answer:
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.

Question 2.
Statement-I: Homolytic cleavage is an asymmetrical one.
Statement-II: A single covalent bond breaks and each of the bonded atoms retains one electron.
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.
(b) Statement-I and II are correct but statement-II is not correct explanation of statement-I.
(c) Statement-I is correct but statement-II is wrong.
(d) Statement-I is wrong but statement-II is correct.
Answer:
(a) Statement-I and II are correct and statement-Il is correct explanation of statement-I.

Question 3.
Heterolysis of propane gives
a) Methyl and ethyl free radicals
b) Methyl carbocation and ethyl free radicals
c) Methyl anion and ethyl carbocation
d) Methyl free radical and ethyl carbocation
Answer:
c) Methyl anion and ethyl carbocation

Question 4.
Which one of the following ¡s correct order of stability of alkyl free radicals?

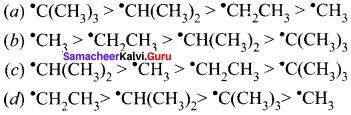
Answer:

Question 5.
Statement-I: Ileterolytic cleavage is unsymmetrical one.
Statement-II: A covalent bond breaks and one of the bonded atom retains the bond pair of electrons.
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.
(b) Statement-I and II are correct but statement-II is not correct explanation of statement-I.
(c) Statement-I is correct but statement-II is wrong.
(d) Statement-I is wrong but statement-II is correct
Answer:
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.

Question 6.
The shape of methyl free radicals is
a) Planar
b) Pyramidal
c) Tetrahedral
d) Linear
Answer:
a) Planar

Question 7.
Which one of the following is correct order of the stability of carbanions?
(a) ^–C(CH₃)₃> ^–CH(CH₃)₂> ^–CH₂-CH₃> ^–CH₃
(b) ^–CH₃> ^–CH₂-CH₃> ^–CH(CH₃)₂> ^–C(CH₃)₃
(c) ^–CH(CH₃), > ^–CH₃> ^–CH₂-CH₃ > ^–C(CH₃)₃
(d) ^–CH₂-CH₃ > ^–CH(CH₃)₂> ^–CH₃> ^–C(CH₃)₃
Answer:
(b) CH₃> CH₂-CH₃> CH(CH₃)₂> C(CH₃)₃

Question 8.
Which of the following contains only three pairs of electrons
a) Carbocation
b) Carbanion
c) Free radical
d) All of these
Answer:
a) Carbocation

Question 9.
Which one of the following is not nucleophile
(a) H₂O
(b) NH₃
(c) R-OH
(d) FeCl₃
Answer:
(d) FeCl₃

Question 10.
In carbonium ion the carbon bearing the positive charge is
a) sp hybridized
b) sp² hybridized
c) sp³ hybridized
d) un hybridized
Answer:
b) sp² hybridized

Question 11.
Which one of the following is nucleophile?
(a) BF₃
(b) AlCl₃
(c) CO₂
(d) R-SH
Answer:
(d) R-SH

Question 12.
The geometry of a methyl carbanion is likely to be
a) Pyramidal
b) Tetrahedral
c) Planar
d) Linear
Answer:
a) Pyramidal

Question 13.
Which one of the following species has a tendency to show +I effect?
(a) -NH₂
(b) -Cl
(c) -C₆H₅
(d) -CH₃
Answer:
(d) -CH₃

Question 14.
Which one of the following has the strongest acidic character?
(a) HCOOH
(b) CH₃COOH
(c) CH₂ClCOOH
(d) CCl₃COOH
Answer:
(d) CCl₃COOH

Question 15.
Which one of the following has the least acidic character?
(a) HCOOH
(b) CH₃COOH
(c) CH₂ClCOOH
(d) CCl₃COOH
Answer:
(b) CH₃COOH

Question 16.
Electrophiles are
a) Electron loving species
b) Electron hating species
c) Nucleus loving reagents
d) Nucleus hating reagents
Answer:
a) Electron loving species

Question 17.
Statement-I: Fluoro acetic acid is stronger acid than acetic acid
Statement-II: Fluorine has high electronegativity and it is facilitate to dissociate the OH bond easily.
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.
(b) Statement-I and II are correct but statement-II is not correct explanation of statement-I.
(c) Statement-I is correct but statement-II is wrong.
(d) Statement-I is wrong but statement-Il is correct
Answer:
(a) Statement-I and II are correct and statement-II is correct explanation of statement-I.

Question 18.
Which one of the following is an example for negative mesomeric effect?
(a) -SH
(b) -SR
(c) -NH₂
(d) -NO₂
Answer:
(d) -NO₂

Question 19.
Methyl carbanium ion is
a) Electrophile
b) Lewis acid
c) Nucleophile
d) Both (a) and (b)
Answer:
c) Nucleophile

Question 20.
Identify the one which does not come under the organic addition reaction
(a) Hydration
(b) Dehydration
(c) Halogenation
(d) Hydro halogenation
Answer:
(b) Dehydration

Question 21.
Primary alcohols undergo which type of reaction to form alkenes?
(a) Elimination
(b) Oxidation
(c) Reduction
(d) Hydrolysis
Answer:
(a) Elimination

Question 22.
Identify the type of reaction
(a) Addition reaction
(b) Elimination reaction
(c) Reduction reaction
(d) Oxidation reaction
Answer:
(d) Oxidation reaction

II. Match the following.

Answer:

III. Fill in the blanks.
Question 1.
The slowest step in the mechanism determines ………..
Answer:
Rate of reaction

Question 2.
Homolytic cleavage occurs under the conditions of ………….
Answer:
High temperature.

Question 3.
During the cleavage of Azobisisobutyronitrile produces species ……….
Answer:
Free radical

Question 4.
The cleavage of C-Br bond in tert-butyl bromide leads to formation of ………..
Answer:
Carbocation

Question 5.
The cleavage of C-H bond in aldehydes Leads to formation of ………….
Answer:
Carbanion

Question 6.
Electron displacement occurring in saturated compounds along a carbon chain is termed as …………
Answer:
Inductive effect

Question 7.
The addition of H to alkene is an example of effect ……….
Answer:
+E

Question 8.
Example for positive mesomeric effect is ………..
Answer:
-OH

Question 9.
Acidity of phenol was explained by …………
Answer:
R-effect

Question 10.
Hydrolysis of alkyl halide is an example for ……….
Answer:
Nucleophilic substitution

Question 11.
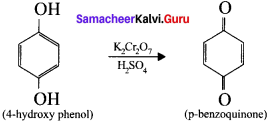
4-hydroxy phenol reacts with acidified potassium dichromate to gives
Answer:
p-Benzoquinone

Question 12.
Enzyme present in apple is
Answer:
Polyphenol oxidase

Question 13.
Benzene reacts with H₂ in the presence of Pt to give
Answer:
Cyclohexane

Question 14.
Alcohol on refluxing with K₂Cr₂O₇ gives……..
Answer:
Carboxylic acid

Question 15.
Carbonyl compounds especially ketones undergo reduction to form ………..
Answer:
Secondary alcohols

Question 16.
Ethane undergoes thrombolytic cleavage to form ………..
Answer:
Methyl free radical

IV. Choose the odd one out.
Question 1.
(a) NH₃
(b) H₂O
(c) CN^–
(d) RSH
Answer:
(c) CN^– It is a negatively charged nucleophile whereas others are neutral nucleophiles.

Question 2.
(a) CO₂
(b) RX
(c) MCl₃
(d) FeCl₃
Answer:
(b) RX. It is a positive charged electrophiles whereas others are neutral electrophiles.

Question 3.
(a) -F
(b) – Cl
(c) – COOH
(d) CH₃O^–
Answer:
(d) CH₃O^–. It is a group carrying negative charge one electron-donating (or) +I group whereas others are -I group.

Question 4.
(a) – C(CH₃)₃
(b) – COOK
(c) – CH(CH₃)₂
(d) – COO^–
Answer:
(b) – COOH. It has -I effect whereas others have a +I effect.

Question 5.
(a) -OH
(b) -NH₂
(c) -SH
(d) -COOH
Answer:
(d) – COOH. It has a negative mesomeric effect whereas others have a positive mesomeric effect.

V. Choose the correct pair.
Question 1.
(a) Homolytic clevage : carbocation
(b) Homolytic clevage : carbanion
(c) Homolytic clevage : free radicals
(d) Heterolytic clevage : free radicals
Answer:
(c) Homolytic clevage : free radicals

Question 2.
(a) + C(CH₃)₃ > ⁺CH(CH₃)₂> ⁺CH₂-CH₃ > ⁺CH₃ : Relative stability of carbocations.
(b) – C(CH₃)₃ > ^–CH(CH₃)₂ > ^–CH₂-CH₃ > ^–CH₃ : Relative stability of carbanion.
(c) OH^–,RO^–, RCOO^– : Neutral nucleophile
(d) AlCl₃, BF₃, FeCl₃ : Positively charged nucleophile
Answer:
(a) + C(CH₃)₃ > ⁺CH(CH₃)₂> ⁺CH₂-CH₃ > ⁺CH₃ : Relative stability of carbocations.

Question 3.
(a) CH₃ – CH₂ – CH₂Br + Alcoholic KOH : Substitution reaction
(b) CH₃ – CH₂ – CH₂Br + Alcoholic KOH : Elimination reaction
(c) CH₃CHO + Acidic dichromate : Reduction reaction
(d) Benzene + Pt + H₂ : Oxidation reaction
Answer:
(b) CH₃ – CH₂ – CH₂Br + Alcoholic KOH : Elimination reaction

VI. Choose the incorrect pair.
Question 1.
(a) – OH,- SH, -NH₂ : Positive mesometic effect
(b) – NO₂ >CO, – COOH : Negative mesomeric effect
(c) – F, – Cl, – NO₂ : Electron withdrawing group
(d) – C(CH₃)₃, – CH(CH₃)₃ – CH₂ – CH₃ : Electron withdrawing group
Answer:
(c) – F, – Cl, – NO₂ : Electron withdrawing group

Question 2.
(a) NH₃ andAmines : Neutral nucleophile
(b) OH^– and RCOO^– : Negative nucleophile
(c) RX and H₃O₃ : Positive electrophile
(d) MCl₃, BF₃ : Negative electrophile
Answer:
(d) AlCl₃, BF₃ : Negative electrophile

Question 3.

Answer:

VII. Assertion and Reason.
Question 1.
Assertion (A): Neutral molecule SnCl₄ can act as an electrophile.
Reason (R): it has vacant ‘d’ orbitais which can accommodate the electrons from others.
(a) Both (A) and (R) are correct and (R) is the correct explanation of (A).
(b) Both (A) and (R) are correct but (R) is not the correct explanation of (A).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Question 2.
Assertion (A) : The C-C bond in ethane is non-polar while the C-C bond in ethyl chloride is polar.
Reason (R) : Chlorine is more electronegative than carbon and hence it attracts the shared pair of electron between C-C in ethyl chloride and it develops a negative charge on Cl and positive charge on Carbon.
(a) Both (A) and (R) are correct but (R) is not the correct explanation of (A).
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Question 3.
Assertion (A): Phenol is more acidic than aliphatic alcohols.
Reason (R): The phenoxide ion is more stabilized than phenol by resonance effect and hence resonance favours ionization of phenol to form H and shows acidity.
(a) Both (A) and (R) are correct and (R) is the correct explanation of(A).
(b) Both (A) and (R) are correct but (R) is not the correct explanation of(A).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct and (R) is the correct explanation of(A).

Question 4.
Assertion (A): The cut apple turns brown.
Reason (R): Cut apple exposes its cells to atmospheric oxygen and the oxidizes the phenolic compound present in it. Due to this enzymatic browning, the cut apple turns brown.
(a) Both (A) and (R) are correct but (R) is not the correct explanation of (A).
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Samacheer Kalvi 11th Chemistry Basic Concepts of Organic Reactions 2 Marks Question and Answers

II. Answer briefly.

Question 1.
What is the mechanism of reaction?
Answer:
Many chemical reactions are depicted in one or more simple steps. Each step passes through an energy barrier, leading to the formation of short-lived intermediates or transition states. The series of simple steps which collectively represent the chemical change, from the substrate to product is called the mechanism of the reaction. The slowest step in the mechanism determines the overall rate of the reaction.

Question 2.
What is the mechanism of the reaction?
Answer:
In organic reactions, that series of simple steps collectively represent the chemical change, from the substrate to product, this is called as the mechanism of the reaction. The slowest step in the mechanism determines the overall rate of the reaction.

Question 3.
What is the Negative Mesomeric effect? Give example.
Answer:
The negative resonance effect occurs when the electrons move towards the substituent attached to the conjugated system. It occurs if the electron-withdrawing substituents are attached to the conjugated system. In such cases, the attached group has a tendency to withdraw electrons through resonance. These electron-withdrawing groups are usually denoted as -R or -M groups.
Example:
NO₂, > C = O, – COOH, – C ≡ N etc..

Question 4.
Explain the homolytic fission of a covalent bond?
Answer:

• Homolytic cleavage is the process in which a covalent bond breaks symmetrically in such way that each of the bonded atoms retains one electron.
• This type of cleavage occurs under high temperatures or in the presence of UV light.
• in a compound containing a non-polar covalent bond formed between atoms of similar electronegativity, in such molecules the cleavage of bonds results in free radicals.
• For example, ethane undergoes homolytic fission to produce, two methyl free radicals.
  

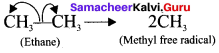
Question 5.
What are free radical initiators?
Answer:
The types of reagents that promote homolytic cleavage in substrate are called as free radical initiators. They are short lived and are highly reactive.

Question 6.
Mention any two examples for free radical initiators?
Answer:
Two examples for free radical initiators

• Azobisisobutyronitnie (AIBN)
• Benzoyl peroxide

Question 7.
Explain the heterolytic fission of a covalent bond?
Answer:

• Heterolytic cleavage is the process in which a covalent bond breaks unsymmetrically such that one of the bonded atom retains the bond pair of electron.
• It results in the formation of a cation and an anion of the two bonded atoms the most electronegative.
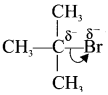
• For example in tert-butyibromide, the C-Br bond is polar as bromine is more electronegative than carbon. Hence the C-Br undergoes heterolytic cleavage to form a terl-butyl carbocation and bromide anion.
  

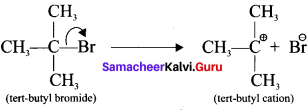
Question 8.
What are carbocations?
Answer:
1. Let us consider the heterolytic fission of the bond C-X present in organic molecule. If atom X has a greater electronegativity than the carbon atom, the former takes away the bonding electron pair and becomes negatively charged while the carbon will lose its electron and thus acquire a positive charge.
2. Such a cationic species carrying a positive charge on carbon are known as carbocation or carhonitim ion.

Question 9.
What are carbanions?
Answer:
Let us consider the heterolytic fission of the bond C-X present in an organic molecule. if the carbon atom has greater electronegativity than the atom X, the former takes away the bonding electron pair and acquires a negative charge. The resulting carbon anion is known as carbanion.

Question 10.
After cutting an apple it turns brown. Why?
Answer:
Apples contain an enzyme called polyphenol oxidase (PPO), also known as tyrosinase. Cutting an apple exposes its cells to atmospheric oxygen and oxidizes the phenolic compounds present in apples. This is called the enzymatic browning that turns a cut apple brown. In addition to apples, enzymatic browning is also evident in bananas, pears, avocados and even potatoes.

Question 11.
Identify which of the following are electrophiles and nucleophiles?

1. NH₃
2. AlCl₃
3. R-SH
4. R-X
5. R-O-R
6. BF₃

Answer:

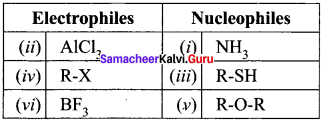
Question 12.
How will you distinguish between electrophiles and nucleophiles?
Answer:
Electrophiles:

• They are electron deficient.
• They are cations.
• They are lewis acids.
• Accept an electron pair.
• Attack on electron-rich sites.

Nucleophites:

• They are electron-rich.
• They are anions.
• They are lewis bases.
• Donate an electron pair.
• Attack on electron-deficient sites.

Question 13.
What are all the sources for the human body that produces free radicals?
Answer:
Sources for the human body produces free radicals,

• The human body is exposed to X-rays.
• Cigarette smoke.
• Industrial chemicals.
• Air pollutants.

Question 14.
In what way free radicals affect the human body?
Answer:

• Free radicals can disrupt cell membranes.
• Increase the risk of many forms of cancer.
• Damage the interior lining of blood vessels.
• leads to a high risk of heart disease and stroke.

Question 15.
How to reduce the effect of free radicals?
Answer:

• Use vitamins and minerals to counter the effects of free radicals.
• Fruits contain antioxidants which decrease the effects of free radicals.

Question 16.
Identify which of the following shows the +I and -I effect?

1. -NO₂
2. -SO₂H
3. -I
4. -OH
5. CH₂O-
6. CH₂–

Answer:

Question 17.
Why chloro acetic acid is stronger acid than acetic acid?
Chioro acetic acid:
Answer:

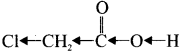
Chioro acetic acid has Cl-group and it has high electronegativity and shows -I effect. Therefore Cl-atom to faciLitate the dissociation of O-H bond very fastly, whereas in the case of acetic acid, has CH₃ group and it shows +I effect, theretòre dissociation of O-H bond will be more difficult. Thus chloro acetic acid is stronger acid than acetic acid.

Question 18.
Explain the positive and negative electromeric effects?
Answer:
1. When an electrophile such as W approaches an alkene molecule, the π electrons are instantaneously shifted to the electrophile and a new bond is formed between carbon and hydrogen. This makes the other carbon electron deficient and hence it acquires a positive charge.

2. When the it electron is transferred towards the attacking reagent, it is called the positive electromeric (+E) effect.

3. Whèn the t electron is transferred away from the attacking reagent it is called the negative electromeric (-E) effect.

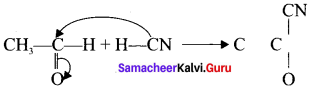
For example : The attack of C\({ N }^{ \ominus }\) on a carbonyl carbon.

Question 19.
Write short notes on the positive mesomeric effect?
Answer:

• The positive mesomeric effect occurs, when the electrons move away from substituent attached to the conjugated system.
• It occurs if the electron releasing substituents are attached to the conjugated system.
• The attached group has a tendency to release electrons through resonance, these electron releasing groups are usually denoted as +R or +M groups.
• Examples: -OH, -SH, -OR, -SR, -NH₂ etc.

Question 20.
Write short notes on the negative mesomeric effect?
Answer:

• The negative mesomeric effect occurs when the electrons move towards the substituent attached to the conjugated system.
• It occurs if the electron-withdrawing substituents are attached to the conjugated system.
  The attached group has a tendency to withdraw electrons through resonance, these electron-withdrawing groups are usually denoted as -R or -M groups.
• Examples:
  

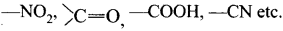
Question 21.
What are addition reactions? Give an example.
Answer:
All organic compounds having double or triple bond adopt addition reactions in which two substances unite to form a single compound. During the addition reaction the hybridization of the substrate changes as only one bond breaks and two new bonds are formed.
Example:

Question 22.
What are elimination reactions? Give an example.
Answer:
In these reactions, two atoms or groups are removed from a molecule without being substituted by other atoms or groups. A new C-C double bond is formed between the carbon atoms to which the eliminated atoms or groups are previously attached. It is always accompanied with change in hybridization.
Example:

Question 23.
What are organic oxidation reactions? Give an example.
Answer:
Most of the oxidation reaction of organic compounds involves gain of oxygen or loss of hydrogen.
Example:

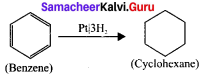
Question 24.
What are organic reduction reactions? Give an example.
Answer:
Most of the reduction reaction of organic compounds involves the gain of hydrogen or loss of oxygen.
Example:

Question 25.
Why cut apple turns a brown colour?
Answer:

• Apples contain an enzyme called polyphenol oxidase (PPO) also known as tyrosinase.
• Cutting an apple exposes its cells to atmospheric oxygen and oxidizes the phenolic compounds present in apples. This is called the “enzymatic browning” that turns a cut apple brown.
• In addition to apples, enzymatic browning is also evident in bananas, pears, avocados, and even potatoes.

Question 26.
What are the different types of organic reactions?
Answer:
Organic compounds undergo many reactions, however, in the actual sense, we can fit all those reactions into the below-mentioned six categories.

1. Substitution reactions
2. Addition reactions
3. Elimination reactions
4. Oxidation and reduction reactions
5. Rearrangement reactions
6. Combination of the above

Question 27.
How will you convert alcohol into aldehyde?
Answer:
When primary alcohol reacts with acidified potassium dichromate to gives aldehyde.

Question 28.
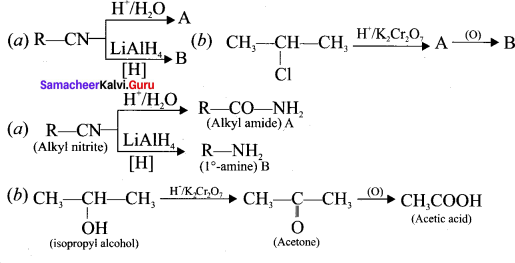
What happen when nitrile undergoes acid hydrolysis?
Answer:
When alkyl nitrile undergoes acid hydrolysis to give amide, which on further hydrolysis to give carboxylic acid.

Question 29.
Complete the following reactions and identify the products?
Answer:

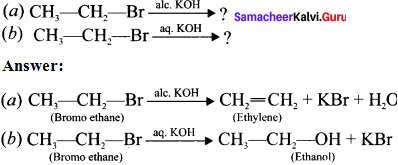
Question 30.
Predict the product for the following reaction.
Answer:

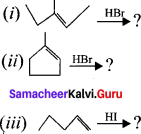
Answer:

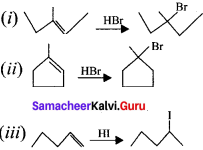
Question 31.
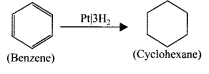
How will you convert benzene into cyclohexane?
Answer:
Benzene undergo catalytic hydrogenation in presence of platinum to give cyclohexane.

Question 32.
Complete the reaction and name the product

Answer:

Question 33.
Identify the product and mention the type of organic reaction.
Answer:

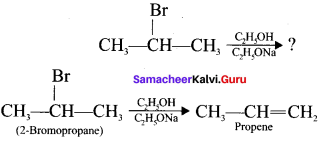
This is one of the elimination reaction.

Question 34.
Complete the following reaction and identify the product.
Answer:

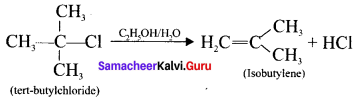
Question 35.
What are substitution reaction?
Answer:
In this reaction an atom or a group of atoms attached to a carbon atom is replaced by a new atom or a group of atoms.

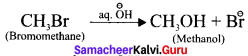
Here, -Br is replaced by -OH group.

Question 36.
How will substitution reactions are classified?
Answer:
Substitution reactions can be classified as,

• Nucleophilic substitution reaction.
• Electrophilic substitution reaction.
• Free radical substitution reaction.

Question 37.
Draw the resonance structures for the following compounds?

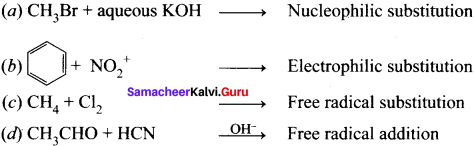
Answer:

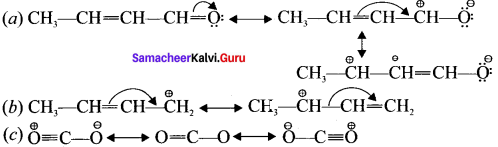
Question 38.
Identify the reagents shown in box in the following equations as nucleophiles or electrophiles.
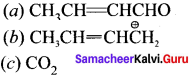
Answer:

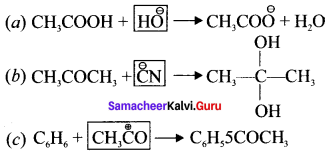
In (a) \(\overset { \ominus }{ OH } \) is nucleophile
In (b) \(\overset { \ominus }{ CN } \) is nucleophile
In (c) CH₃\(\overset { \ominus }{ CO } \) is electrophile

Question 39.
Classify the following reactions in one of the reaction type of organic reaction.
Answer:
(a) CH₃CH₂Br + \({ SH }^{ \ominus }\) → CH₃CH₂SH + \({ Br }^{ \ominus }\)
(b) (CH₃)₂C = CH₂ + HCI (CH₃)₂CCl – CH₃
(c) CH₃CH₂Br + \({ OH }^{ \ominus }\) → CH₂ = CH₂ + H₂O + \({ Br }^{ \ominus }\)
(a) Nucleophilic substitution reaction.
(b) Electrophilic addition reaction.
(c) Elimination reaction.

Question 40.
Which electron displacement effect explain the following correct orders of acidity of the carboxylic acids?
Answer:
CH₃CH₂COOH > (CH₃)₂ CHCOOH > (CH₃)₃C COOH
As the number of alkyl group increases, +I effect increases and it strengthen the O-H bond. i.e., O-H bond dissociation is very difficult.

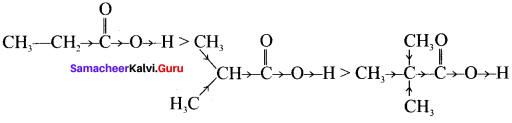
Therefore +I effect explain the correct orders of acidity of the carboxylic acids.

Question 41.
Which of the two, NO₂CH₂CH₂\({O}^{ \ominus }\) or CH₃CH₂\({O}^{ \ominus }\) is expected to be more stable and why?
Answer:

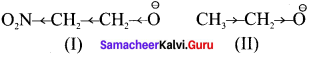
(I) is more stable than (II) because NO₂ group has -I effect and hence it tends to disperse the -ve charge on the 0-atom. In contrast., CH₃CH, has +I effect. It therefore, tends to intensify the -ve charge and hence destabilizes it.

Samacheer Kalvi 11th Chemistry Basic Concepts of Organic Reactions 5 Marks Questions and Answers

Question 1.
Explain electron movement in organic reactions.
Answer:
All organic reactions can be understood by following the electron movements.

• Lone pair becomes a bonding pair.
• Bonding pair becomes a lone pair.
• A bond breaks and becomes another bond.

The electron movement depends on the nature of the substrate, reagent and the prevailing conditions.
Type – 1.
A lone Pair to a bonding pair

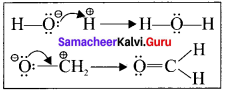
Type – 2.
A bonding pair to a lone Pair

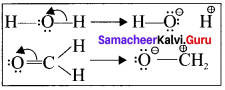
Type – 3.
A bonding pair to an another bonding pair

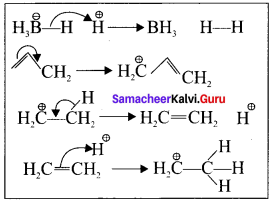
Question 2.
How does inductive effect influence the reactivity and acidity of carboxylic acids?
Answer:
(a) Reactivity:

• When a highly electronegative atom such as halogen is attached to a carbon then it makes the C—X bond polar.
• In such cases the -I effect of halogen facilitates the attack of an incoming nucleophile at the polarized carbon and hence increases the reactivity.
  
• If a -I group is attacher neared to a carbonyl carbon, it decreases the availability of electron density on the carbonyl carbon and hence increases the rate of the nucleophilic addition reaction.

(b) Acidity of carboxylic acid:

• When a halogen atom is attached to the carbon which is neared to the carboxylic acid group, its -I effect withdraws the bonded electrons towards itself and makes the ionization of H+ easy.
• The acidity of various chioro acetic acid is in the following order. Cl₃C-COOH > Cl₂CHCOOH > ClCH₂COOH The strength of the acid increases with increase in the effect of the group attached to the carboxyl group.
• Similarly the following order of acidity in the carboxylic acids is due to the +1 effect of alkyl group. (CH₃)₃CCOOH < (CH₃)₂CHCOOH <CH₃COOH

Question 3.
Explain the acidic nature of phenol.
Answer:

• Resonance is useful in explaining certain properties such as acidic of phenol.
• The phenoxide ion is more stabilized than phenol by resonance effect.
• The resonance favours ionisation of phenol to form H+ and shows acidity.
  
  phenoxide ion resonance structures.
  
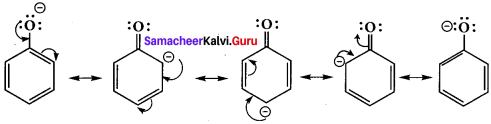
• The above structures shows that there is a charge separation in the resonance structure of phenol which needs energy whereas there is no such hybrid structures in the case of phenoxide ion. This increases stability accounts for the acidic character of phenol.

Question 4.
How does the hyperconjugation effect explain the stability of alkenes?
Answer:

• The relative stability of various classes of carhonium ions may be explained by the number of no-bond resonance structures that can be written for them.
• Such structures are arrived by shifting the bonding electrons from an adjacent C-H bond to the electron-deficient carbon.
• in this way, the positive charge originally on carbon is dispersed to the hydrogen. This manner of electron release by assuming no bond character in the adjacent C-H bond is called hyperconjugation or Baker- Nathan effect.
• The greater the hyperconjugation, the greater will be the stability of the compound. The increasing order of stability can be shown as:
  
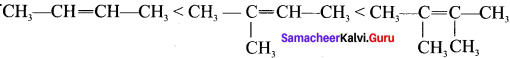
• Alkyl group increases in the C=C double bond carbon, hyperconjugation increases, and stability of that organic compound also increases.

Question 5.
Explain the types of addition reactions?
Answer:
Addition reactions are classified into three types. They are,

1. Electrophilic addition reaction
2. Nucleophilic addition reaction
3. Free radical addition reaction

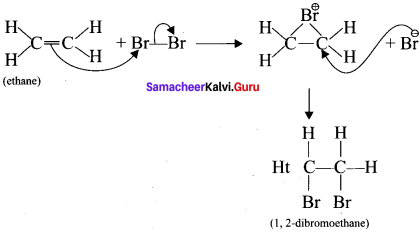
1. Electrophilic addition reaction:
An electrophilic addition reaction can be described as an addition reaction in which a reactant with multiple bonds as in a double or triple bond undergoes has it air bond broken and two new a bond are formed.

2. Nucleophilic addition reaction:
A nucleophilic addition reaction is an addition reaction where a chemical compound with an electron-deficient or electrophilic double or triple bond, reacts with a nucleophilic which is an electron-rich reactant with the disappearance of the double bond and creation of two new single or bonds.

3. Free radical addition reaction:
it is an addition reaction in organic chemistry involving free radicals. The addition may occur between a radical and a non radical or between two radicals.

Question 6.
Explain the types of substitution reaction?
Answer:
Substitution reactions are classified into three types. They are,

1. Nucleophilic substitution reaction.
2. Electrophilic substitution reaction.
3. Free radical substitution reaction.

1. Nucleophilic substitution reaction:
A nucleophilic substitution reaction in organic chemistry is a type of reaction where a nucleophilic gets attached to the positive charged atoms or molecules of the other substance. A good example of a nucleophilic substitution reaction is the hydrolysis of alkyl bromide, under the basic conditions where in the nucleophile is nothing but the base H. whereas the leaving group is the Br°. The reaction for the following is as give below.

2. Electrophilic substitution reaction:
The electrophilic substitution reaction involves the electrophiles. The electrophilic reactions occur mostly with the aromatic compounds. This types of substitution reaction arc basically defined as those chemical reactions where the electrophile replaces the functional group in a compound but not the hydrogen atom, sometimes hydrogen atom can be also replaced by electrophiles.
For example:

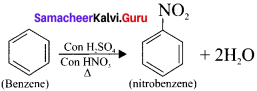
3. Free radical substitution reaction:
Free radical substitution reaction involving free radicals arc a reactive intermediate.
A – X + Y → A – Y + X
CH₄ + Cl → CH + HCl
CH₃ + Cl → CH₃Cl (methyl chloride)

Question 7.
For the following bond cleavages use curved-arrows to show the electron flow and classify each as homolytic or heterolytic fission. Identify reactive intermediate produced as free radical,, carbocation and carbanion?

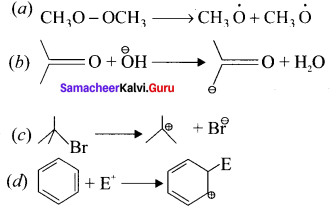
Answer:

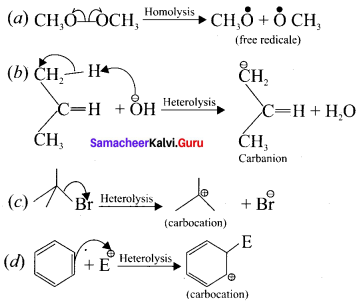
Question 8.
An organic compound (A) has a molecular formula C₂H₆O it is one of the primary alcohol. A reacts with acidified potassium dichromate to give B. B on further undergoes to oxidation reaction to give C. C on reacts with SOCl₃ to give D which ¡s chlorinated product. Identify A,B,C and D, explain with equation.
Answer:
1. C₂H₆O is CH₃-CH₂-OH which is a primary alcohol (A)
2. CH₃-CH₂-OH (A) reacts with H⁺/ K₂Cr₂O₇ to give acetaldehyde (B)

3. CH₃CHO (B) which on further oxidation to give acetic acid (C).

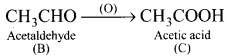
4. Acetic acid reacts with SOCl₂ to give acetyl chloride (D).

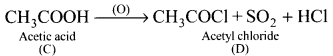
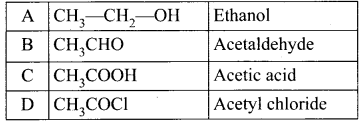
Question 9.
An organic compound (A) of a molecular formula C₂H₄ which is a simple alkene. A reacts with dil H₂S0₄ to give B. A again reacts with Cl₂ to give C. Identify AB and C and write the equations.
Answer:
1. C₂H₂ is CH₂=CH₂ is a simple alkene. A is ethylene.
2. Ethylene (A) reacts with dii H₂SO₄ to give ethanol (B)

3. Ethylene (A) reacts with Cl, to give 1.2 dichloro ethane (C)

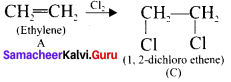
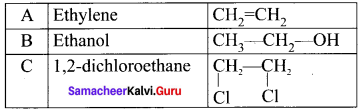
Question 10.
Complete the reactions and identify the products.
Answer:

Students can Download Chemistry Chapter 15 Environmental Chemistry Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Chemistry Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Chemistry Solutions Chapter 15 Environmental Chemistry

Samacheer Kalvi 11th Chemistry Environmental Chemistry Textual Evaluation Solved

Samacheer Kalvi 11th Chemistry Environmental Chemistry Multiple Choice Questions

Question 1.
Th gaseous envelope around the earth is known as atmosphere. The region lying between an altitude of 11-50 km is –
(a) Troposphere
(b) Mesophere
(c) Thermosphere
(d) Stratosphere
Answer:
(d) Stratosphere

Question 2.
Which of the following is natural and human disturbance in ecology?
(a) Forest fire
(b) Floods
(c) Acid rain
(d) Greenhouse effect
Answer:
(a) Forest fire

Question 3.
Bhopal Gas Tragedy is a case of –
(a) thermal pollution
(b) air pollution
(c) nuclear pollution
(d) land pollution
Answer:
(b) air pollution

Question 4.
Haemoglobin of the blood forms carboxyhaemoglobin with –
(a) Carbon dioxide
(b) Carbon tetrachioride
(c) Carbon monoxide
(d) Carbonic acid
Answer:
(c) Carbon monoxide

Question 5.
Which sequence for greenhouse gases is based on GWP?
(a) CFC > N₂O > CO₂ > CH₄
(b) CFC > CO₂ > N₂O > CH₄
(c) CFC > N₂O > CH₄ > CO₂
(d) CFC > CH₄ > N₂O > CO₂
Answer:
(c) CFC > N₂O > CH₄ > CO₂

Question 6.
Photo chemical smog formed in congested metropolitan cities mainly consists of –
(a) Ozone, SO₂ and hydrocarbons
(b) Ozone, PAN and NO₂
(c) PAN, smoke and SO₂
(d) Hydrocarbons, SO₂ and CO₂
Answer:
(b) Ozone, PAN and NO₂

Question 7.
The pH of normal rain water is –
(a) 6.5
(b) 7.5
(c) 5.6
(d) 4.6
Answer:
(c) 5.6

Question 8.
Ozone depletion will cause –
(a) forest fires
(b) eutrophication
(c) bio magnification
(d) global warming
Answer:
(d) global warming

Question 9.
Identify the wrong statement in the following.
(a) The clean water would have a BOD value of more than 5 ppm
(b) Greenhouse effect is also called as Global warming
(c) Minute solid particles in air is known as particulate pollutants
(d) Biosphere is the protective blanket of gases surrounding the earth
Answer:
(a) The clean water would have a BOD value of more than 5 ppm

Question 10.
Living in the atmosphere of CO is dangerous because it –
(a) Combines with O₂ present inside to form CO₂
(b) Reduces organic matter of tissues
(c) Combines with haemoglobin and makes it incapable to absorb oxygen
(d) Dries up the blood
Answer:
(c) Combines with haemoglobin and makes it incapable to absorb oxygen

Question 11.
Release of oxides of nitrogen and hydrocarbons into the atmosphere by motor vehicles is prevented by using –
(a) grit hamber
(b) scrubbers
(c) trickling filters
(d) catalytic convertors
Answer:
(c) trickling filters

Question 12.
Biochemical oxygen Demand value less than 5 ppm indicates a water sample to be
(a) highly polluted
(b) poor in dissolved oxygen
(c) rich in dissolved oxygen
(d) low COD
Answer:
(c) rich in dissolved oxygen

Question 13.
Match the list I and list II and select the correct answer using the code given below in the list:

Answer:

Question 14.
Match the list I and list II and select the correct answer using the code given below in the list

Answer:

Question 15.
Assertion (A) : if BOD level of water in a reservoir is more than 5 ppm it is highly polluted.
Reason(R) : High biological oxygen demand means high activity of bacteria in water
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
Answer:
(d) (iv)

Question 16.
Assertion (A) : Excessive use of chlorinated pesticide causes soil and water pollution.
Reason (R) : Such pesticides arc non-biodegradable.
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
Answer:
(a) (i)

Question 17.
Assertion (A) : Oxygen plays a key role in the troposphere.
Reason (R) : Troposphere is not responsible for all biological activities
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
Answer:
(d) (iv)

Samacheer Kalvi 11th Chemistry Environmental Chemistry Short Answer Questions

Question 18.
Dissolved oxygen in water is responsible for aquatic life. What processes are responsible for the reduction in dissolved oxygen in water’?
Answer:

• Organic matter such as leaves, grass, trash can pollute water. Microorganisms present in water can decompose these organic matter and consume dissolved oxygen in water.
• Eutrophication is a process by which water bodies receive excess nutrients that stimulates excessive plant growth. This enhanced plant growth in water bodies is called algal bloom.
• The growth of algae in extreme abundance covers the water surface and reduces the oxygen concentration in water. Thus, bloom-infeded water inhibits the growth of other. living organisms in the water body.
• This process in which the nutrient rich water support a dense plant population, kills animal life by depriving it of oxygen and results in loss of biodiversity is known as eutrophication.

Question 19.
What would happen, if the greenhouse gases were totally missing in the earth’s atmosphere?
Answer:

• The primary greenhouse gases in Earth’s atmosphere are water vapour, carbon dioxide, methane, nitrous oxide and ozone.
• Naturally occurring greenhouse gases allow solar radiations to reach the earth’s surface, while trapping radiations from the earth on its way back out to space.
• There would he no life on Earth without the warmth provided by this natural greenhouse gases.
• In the absence of greenhouse gases. the average temperature of the earth will decrease drastically. As a result. life on Earth would be impossible.

Question 20.
Define smog.
Answer:

• Smog is a combination of smoke and fog which form droplets that remains suspended in the air.
• Smog is a chemical mixture of gases that forms a brownish yellow haze. It mainly consists of ground level ozone, oxides of nitrogen, volatile organic compounds, SO₂, acidic aerosols and some other gases.

Question 21.
Which is considered to be earth’s protective umbrella? Why?
Answer:

• At high altitudes in the atmosphere consists of a layer of ozone (O₂) which acts as an umbrella for harmful UV radiations. Ozone is considered to be earth’s protective umbrella.
• It protects us from harmful effects of UV-radiations of the sun such as skin cancer.
• Ozone layer prevent the UV radiations to reach the earth surface. So it acts as an umbrella for the Earth.

Question 22.
What are bio-degradable and non-biodegradable pollutants?
Answer:

• The pollutants which can be easily decomposed by the natural biological processes are called biodegradable pollutants. For example plant wastes, animal wastes.
• The pollutants which cannot be decomposed by the natural biological processes are called non-biodegradable pollutants. For example, metal wastes such as Hg and Pb, D.D.T. plastics, nuclear vastcs.

Question 23.
From where does ozone come in the photochemical smog?
Answer:

• Photochcrnical smog is formed by the combination of smoke, dust and fog with air pollutants in the presence of sunlight.
• Chemically it is oxidising in nature because of high concentration of oxidising agents such as NO₂ and O₂. So it is also called oxidising smog.
• Photochemical smog is formed by following reactions:
• N₂ + O₂ → 2NO
  2NO + O₂ → 2NO₂
  
  (O) + O₂ → O₃
  O₃ + NO → NO₂ + O₂
  
• NO and O₃ arc strong oxidizing agents and they can react with unburnt hydrocarbons in polluted air to form formaldehyde, acrolcin and PAN.

Question 24.
A person was using water supplied by corporation. Due to shortage of water he started using underground water. He felt laxative effect. What could be the cause?
Answer:
Drinking water containing moderate level of sulphatcs is harmless. But excessive concentration (>500 ppm) of suiphates in drinking water causes laxative effect.

Question 25.
What is green chemistry?
Answer:

• Green chemistry is a chemical philosophy encouraging the design of products and processes that reduces or eliminates the use and generation of hazardous substances.
• Efforts to control environmental pollution resulted in development of science for the synthesis of chemicals favorable to environment.
• Green chemistry means science of environmentally favorable chemical synthesis.

Question 26.
Explain how does greenhouse effect cause global warming.
Answer:

• The earth’s atmosphere allows most of the visible light from the sun to pass through and reach the earth’s surface. As earth’s surface is heated by sunlight, it radiates a part of this energy back towards the space as longer IR wavelengths.
• Some of the heat is trapped by CH₂, CO₂. CFCs and water vapour present in the atmosphere. They absorb IR radiations and block a large portion of earth’s emitted radiations.
• The radiations thus absorbed is partly remitted to the earth’s surface. Therefore the earth’s surface gets heated up by a phenomenon called greenhouse effect.
• Thus greenhouse effect is defined as the heating up of the earth surface due to trapping of infrared radiations reflected by earth’s surface by CO₂ layer in the atmosphere. The heating up of the earth through the greenhouse effect is called global warming.

Question 27.
Mention the standards prescribed by BIS for quality of drinking water.
Answer:
Standard characteristics prescribed for deciding the quality of drinking water by BIS are as follows:

Question 28.
How does classical smog differ from photochemical smog?
Answer:
Classical smog:

• Classical smog is caused by coal-smoke and fog.
• It occurs in cold humid climate.
• The chemical composition is the mixture of SO₂, SO₃ gases and humidity.
• Chemically it is reducing in nature because of high concentration of SO, and so it is also called reducing smog.
• It is primarily responsible for acid rain.
• It also causes bronchial irritation.

Photochemical smog:

• Photochemical smog is cause by photochemical oxidants.
• It occurs in warm, dry and sunny climate.
• The chemical composition is the mixture of NO₂ and O₃ gases.
• Chemically it is oxidising in nature because of high concentration of oxidising agents such as NO₂ and O₃
• and so it is also called oxidising smog.
• It causes irritation to eyes, skin and lungs and increase the chances of asthma.
• It causes corrosion of metals, stones

Question 29.
What are particulate pollutants? Explain any three.
Answer:
1. Particulate pollutants are small solid particles, and liquid droplets suspended in air.
Examples:
dust, pollen, smoke, soot and liquid aerosols.

2. Types of Particulates:
Particulates in the atmosphere may be of two types:

• viable particulate and
• non-viable particulate.

3.The viable particulates are small size living organisms such as bacteria, fhngi, moulds and algae which are dispersed in air.

4. The non-viable particulates are small solid particles and liquid droplets suspended in air. There are four types of non-viable particulates in the atmosphere. They are
(a) Smoke
(b) Dust
(c) Mist
(d) Fumes

5. Smoke:
Smoke particulate consists of solid particles formed by combustion of organic matter. For example, cigarette smoke, oil smoke, smokes from burning of fossil fuels, garbage and dry leaves.

6. Dust:
It is composed of fine solid particles produced during crushing and grinding of solid materials. For example, sand from sand blasting, saw dust from wood works and fly ash from power generating units.

7. Mist:
They are formed by particles of sprayed liquids and condensation of vapours in air. For example, sulphuric acid mist, herbicides and insecticides sprays can form mists.

8. Fumes:
They are obtained by condensation of vapours released during sublimation, distillation, boiling and calcination and by several other chemical reactions.
For example:
organic solvents, metals and metallic oxides.

Question 30.
Even though the use of pesticides increases the crop production, they adversely affect the living organisms. Explain the function and the adverse effects of the pesticides.
Answer:
1. Pesticides are the chemicals that are used to kill or stop the growth of unwanted organims. But these pesticides can affect the health of human beings. Pesticides are classified as
(a) insecticides,
(b) Fungicides and
(c) Herbicides.

(a) Insecticides:
Insecticides like DDT, BHC, Aidrin can stay in soil for a long period of time and are absorbed by soil. They contaminate root crops like carrot, radish.

(b) Fungicides:
Organomercury compounds dissociate in soil to produce mercury which is highly toxic.

(c) Herbicides:
They are used to control unwanted plants and are also known as weed killers. Eg, Sodium chlorate, sodium nitrate. They are toxic to mammals.

Question 31.
Ethane bums completely in air to give CO₂. while in a limited supply of air gives CO. The same gases are found in automobile exhaust. Both CO and CO₂ are atmospheric pollutants

1. What is the danger associated with these gases?
2. How do the pollutants affect the human body?

Answer:
Danger associated with CO and CO₂ & health hazards to human body
(a) Carbon monoxide binds with haemoglohin and form carboxyhaemoglobin which impairs normal oxygen transport by blood and hence the oxygen carrying capacity of blood is reduced. This oxygen deficiency results in headache, tension, dizziness, loss of consciousness, blurring of eyesight and cardiac arrest.

(b) Increase in CO₂ level in the atmosphere is responsible for global warming. It causes headache and nausea.

Question 32.
On the basis of chemical reactions involved, explain how do CFC’s cause depletion of ozone layer in stratosphere?
Answer:
(i) The chioro-Iluoro derivatives of methane and ethane are named Freons (CFC’s). They slowly pass from troposphere to stratosphere. They stay for a very longer period of about 50-100 years. In the presence of UV radiations, CFC’s break up into chienne free radicals.

Cl• + O₃ → { ClO }^{ \bullet } + O₂
ClO• + O → { Cl }^{ \bullet } + O₂

(iii) Chlorine radical is regenrated in the course of the reaction. Due to this continuous attack of Cl free radicals, thinning of ozone layer takes place which leads to the formation of ozone hole.

(iv) Li is estimated that for every reactive chlorine atom generated in the stratosphere 1,00,000 molecules of ozone are depleted.

Question 33.
How is acid rain formed? Explain its effect.
Answer:
1. Rain water has a pli of 5.6 due to the dissolution of CO., into it. Oxides of sulphur and nitrogen in the atmosphere may be absorbed by droplets of water that make up the clouds and get chemically converted into sulphuric acid and nitric acid. Due to this the pH of rain water drops below the level of 5.6. Hence it is called acid rain.

2. Acid rain is a by-product of sulphur and Nitrogen oxides in the atmosphere. Burning of fossil fuels in power stations, furnaces and petrol, diesel in motor engines produce SO₂ and NO₂ gases. They are converted into H₂SO₄ and HNO₃ by the reaction with oxygen and water.

3. 2SO₂ + O₃ + 2H₂O → 2H₂SO₄
4NO₂ + O₂+ 2H₂O → 4HNO₃

Harmful effects of acid rain:
1. Acid rain causes damage to buildings made us of marbles. This attack on marble is termed as stone leprosy.
CaCO₃ + H₂SO₂ CaSO₄ + H₂O + CO₂↑

2. Acid rain affects plant and animal life in aquatic ecosystem.

3. It is harmful For agriculture, as it dissolves in the earth and removes the nutrients needed for the growth of plants.

4. It corrodes water pipes resulting in the leaching of heavy metals such as iron, lead and copper into drinking water which have toxic effects.

5. it causes respiratory ailment in humans and animals.

Question 34.
Differentiate the following:

1. BOD and COD
2. Viable and non-viable particulate pollutants

Answer:
Biochemical oxygen demand (BOD):

• The total amount of oxygen (in milligrams) consumed by microorganisms in decomposing the waste in one litre ut water at 20°C for a period of 5 days is called biochemical oxygen demand (BOD).
• its value is expressed in ppm.
• DOD is used as a measure of degree ofwater pollution.
• BOD is only a measurement of consumed oxygen by microorganims to decompose the organic matter.
  Clean water would have BOD value less than 5 ppm.

Chemical ox gen demand (COD):

• Chemical oxygen demand is defined as the amount of oxygen required by the organic matter in a sample of water for its oxidation by a strong oxidising agent like K₇Cr₂O₇ in acidic medium for a period of 2 hours.
• Its value is expressed in mg / litre.
• COD is a measure of amount of organic compounds in a water sample.
• COD refers to the requirement of dissolved oxygen for both the oxidation of organic and inorganic constituents.
• Clean water would have COD value greater than 250 mg/litre.

2. Viable and non-viable particulate pollutants
Viable pollutants:

• The viable particulates are small size living organisms such as bacteria, fungi. moulds, algae which are dispersed in air.
• They are all organic particulates.
• They contain living organisms.
•  Eg. ftingi, bacteria, algae, moulds. Viable particles are the particles with at least one microorganism affecting the sterility of the product.

Non-viable pollutants:

• The non-viable particulates are small solid particles and liquid droplets suspended in air.
• They are all inorganic particulates.
• They contain non-living organisms.
• Eg. Smoke, dust, mist, fumes.
• Non-viable particles are the particles without microorganisms but act as transporting agent for viable particles.

Question 35.
Explain how oxygen deficiency is caused by carbon monoxide in our blood? Give its effect.
Answer:

1. Carbon monoxide binds with haemoglobin and form carboxy the haemoglobin which impairs normal oxygen transport by blood and hence the oxygen carrying capacity of blood is reduced.
2. This oxygen deficiency results in headache, dizziness, tension, loss of consciousness, blurring of eyesight and cardiac arrest.

Question 36.
What are the various methods you suggest lo protect our environment from pollution?
Answer:
Methods to control environmental pollution:

• Waste management Environmental pollution can be controlled by proper disposal of wastes.
• Recycling A large amount of disposed waste materials can he reused by recycling the waste, thus it reduces the landfill. –
• By substitution of less toxic solvents for highly toxic ones are used in industrial processes.
• By growing more trees.
• By using fuels with lower sulphur content.
• By control measures in vehicle emissions which are adequate.

Samacheer Kalvi 11th Chemistry Environmental Chemistry Additional Questions Solved

I. Choose the correct answer

Question 1.
Which one of the following is bio-degradable pollutant?
(a) DDT
(b) Plastics
(c) Mercury
(d) Wood
Answer:
(d) Wood

Question 2.
Which one of the following gases is not present in troposphere?
(a) N₂O₂
(b) CO₂
(c) N₂
(d) water vapours
Answer:
(c) N₂

Question 3.
Which of the following pair of’ oxides is responsible for acid rain?
(a) SO₃ + NO₂
(b) CO₂ + CO
(c) N₂O + CH₄
(d) O₂ + H₂
Answer:
(a) SO₃ + NO₂

Question 4.
Which one of the following is produced as a result of incomplete combustion of coal’?
(a) CO₂
(b) CO
(c) SO₂
(d) SO₃
Answer:
(b) CO

Question 5.
Which of the following is not a greenhouse gas’?
(a) CO
(b) O₃
(c) CH₄
(d) Water vapours
Answer:
(a) CO

Question 6.
Photochemical smog occurs in warm, dry and sunny climate. One of the following is not among-st the components of photochemical smog. Identify it.
(a) NO₂
(b) O₃
(c) SO₂
(d) Unsaturated hydrocarbons
Answer:
(c) SO₂

II. Match the following
1.

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

III. Fill in the blanks

Question 1.
An example for biodegradable pollutant is ………
Answer:
plant waste.

Question 2.
An example for non-biodegradable pollutant ………
Answer:
metal waste.

Question 3
……… is the lowest layer of atmosphere.
Answer:
Troposphere.

Question 4.
Ozone is present in ……… layer of the atmosphere.
Answer:
Stratosphere.

Question 5
……… is called blue planet.
Answer:
Earth.

Question 6.
About 80% of the mass of the atmosphere is present in ………
Answer:
Troposphere.

Question 7.
……… will reduce the oxygen carrying capacity of blood.
Answer:
CO

Question 8
……… gas is used in the process of photosynthesis.
Answer:
CO₂

Question 9.
……… gas potentially damage plant leaves and retard photosynthesis.
Answer:
NO₂

Question 10.
……… is formed by incomplete combustion of coal.
Answer:
CO₂

Question 11.
……… binds with haemoglobin and reduce the oxygen carrying capacity of blood.
Answer:
CO

Question 12.
……… is carcinogenic and causes irritation in eyes and mucous membrane.
Answer:
PAH

Question 13.
The earths surface get heated up by a phenomenon called ………
Answer:
Greenhouse effect

 

Question 14.
The main constituent of layer responsible for global warming is ………
Answer:
CO₂

Question 15.
Earth’s average surface temperature would be only about ………
Answer:
-18°C

Question 16.
The pH of rain water is normally ………
Answer:
5.6

Question 17.
……… pair of compounds is present in acid-rain water.
Answer:
HNO₃ + H₂SO₄

Question 18.
……… is an example of viable particulate.
Answer:
Bacteria.

Question 19.
……… is an example of non-viable particulate matter.
Answer:
Cement dust.

Question 20.
Particulate pollutants will result in the health hazard named as ………
Answer:
pneimoconiosis.

Question 21.
Coal miners may suffer from ………
Answer:
Black lung disease.

Question 22.
Textile workers may suifer from ………
Answer:
White lung disease.

Question 23.
………….. aftect childrcns brain. interfers with maturation of RBC’s and even causes cancer.
Answer:
Lead.

Question 24.
……… can be used to reduce particulate pollutant.
Answer:
electrostatic precipitator

Question 25.
……… is the combination of smoke and fog.
Answer:
Smog.

Question 26.
Classical smog called London smog contains ………
Answer:
Coal-smoke and fog.

Question 27.
Classical smog is otherwise called ………
Answer:
reducing smog.

Question 28.
Photochemical smog is otherwise called ………
Answer:
Los angeles smog.

Question 29.
The three main components of photochemical sinog are ………
Answer:
Hydrogen sulphide. dust and PAN.

Question 30.
……… plantation can metabolise nitrogen oxide and control photochemical smog.
Answer:
Pinus tree.

Question 31.
……… acts as an umbrella for the earth and prevent harmful UV radiations.
Answer:
ozone.

Question 32.
……… pair of compounds is found to be highly responsible for depletion of ozone layer.
Answer:
Nitric oxide + CFC

Question 33.
Freons are ………
Answer:
Chiorofluoroalkanes.

Question 34.
Ozone layer is depicted by the reactive ………
Answer:
Chlorine atom.

Question 35.
Examples for water borne diseases are ………
Answer:
Dysentery and cholera.

Question 36.
The standard pH of drinking water is ………
Answer:
6.5 to 8.5

Question 37.
The essential elements for soil are ………
Answer:
N,P,K

Question 38
……… is a better alternative for carnicogentic benzene.
Answer:
Xylene.

Question 39.
The alternate solvent used instead of tetrachioroethYlefle in dry cleaning is ………
Answer:
Liquefied CO₂

Question 40.
……… is used for bleaching clothes in laundry.
Answer:
H₂O₂

Question 41.
……… is used to bleach paper.
Answer:
H₂O₂

Question 42.
……… is the most safest pesticide.
Answer:
Neem based pesticide.

Question 43.
……… acid is most abundant ¡n acid rain.
Answer:
H₂SO₄

Question 44.
……… causes less pollution.
Answer:
CO₂

Question 45.
Besides CO₂ the other greenhouse gas is ………
Answer:
CH₄

Question 46.
BOD is a measure of ………
Answer:
Organic pollutant in water.

Question 47.
The pollutant released in Bhopal gas tragedy was ………
Answer:
Methyl isocyanate.

Question 48.
The greatest affinity for haemoglobin in shown by ………
Answer:
CO

Question 49.
Eutrophication causes reduction in ………
Answer:
dissolved oxygen.

IV Choose the odd one out

Question 1.
(a) Plant waste
(b) DDT
(c) Plastic
(d) Nuclear waster
Answer:
(a) Plant waste. It is biodegradable pollutant whereas others are non-biodegradable pollutants.

Question 2.
(a) Plant waste
(b) Animal wastes
(c) Paper
(d) Nuclear waste
Answer:
(d) Nuclear waste. It is non-biodegradable pollutant whereas others are biodegradable wastes.

Question 3.
(a) N₂O₂
(b) CO₂
(c) H₂O (Vap)
(d) O₃
Answer:
(d) O₃ It is present in stratosphere whereas others are present in troposphere.

Question 4.
(a) O₂⁺
(b) O⁺
(c) N₂
(d) NO⁺
Answer:
(c) N₂. ills present in mesosphere whereas others are present in thermosphere.

Question 5.
(a) N₂
(b) O₂
(c) O₃
(d) N₂O₂
Answer:
(d) N₂O₂ It is present in troposphere whereas others are present in stratosphere.

Question 6.
(a) CH₄
(b) CO
(c) CO₂
(d) CFC
Answer:
(b) CO. It is a poisonous gas whereas others are responsible for green house effect.

V. Choose the correct pair

Question 1.
(a) CCF : Green house effect
(b) CO : Carcinogenic
(c) PAH : Acid rain
(d) NO : Lung injury
Answer:
(a) CCF : Green house effect

Question 2.
(a) NO₂ : Green house effect
(b) CFC : asthma and lung injury
(c) PAH : carcinogenic
(d) CO₂ : green house effect
Answer:
(a) NO₂ : Green house effect

Question 3.
(a) Classical smog : NO₂ and O₂
(b) London smog : SO₂, SO₂ and humidity
(c) Photochemical smog : CO₂ and CO
(d) Los Angel smog : NO₂ and NO₃
Answer:
(b) London smog : SO₂ , SO₂ and humidity

VI. Choose the incorrect pair

Question 1.
(a) Photochemical smog : NO₂ and O₂
(b) Classical smog : SO₂, SO₃ and humidity
(c) Smog : Smoke and fog
(d) Non viable particulate : Algae, Fungi
Answer:
(d) Non viable particulate : Algae, Fungi

Question 2.
(a) Viable particulate : bacteria, fungi
(b) Non viable particulate : smoke, dust
(c) Acid rain : HCl + HNO₂
(d) Photochemical smog : NO₂ + O₃
Answer:
(c) Acid rain : HCl + HNO₂

Question 3.
(a) Lead : Damage to kidney, liver
(b) Sulphate : Laxative effect
(c) Nitrage : Blue baby syndrome
(d) TDS : Damage to bone and teeth
Answer:
(d) TDS : Damage to bone and teeth

Question 4.
(a) Insecticides : DDT. BCHs
(b) Herbicides : Organo mercury compounds
(c) Herbicides : Sodium chlorate, sodium arsenite
(d) Industrial waste : Mercury. copper
Answer:
(b) Herbicides : Organo mercuiy compounds

VII. Assertion & Reason
Assertion (A) : Depletion of ozone layer causes skin cancer.
Reason (R) : Depletion olozone layer will allow more UV rays to reach the earth surface and cause skin cancer.
(a) Both (A) and (R) are correct and (R)is the correct explanation of (A).
(b) Both (A) and (R) are correct but (R) is not the correct explanation of (R).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Question 2.
Assertion (A) : UV radiations damages the fish productivity.
Reason (R) : UV radiations affect the growth of phytoplankions as a result food chain in ocean is disturbed.
(a) Both (A) and (R) are correct hut (R) is not the correct explanation of (A).
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).
(c) (A) is correct but (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(b) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Question 3.
Assertion (A) : The pH ol acid rain is less than 5.6.
Reason (R) : CO, present in the atmosphere dissolves in rain water and forms carbonic acid,
(a) Both (A) and (R) are correct and (R) is the correct explanation of (A).
(b) Both (A) and (R) are correct hut (R) is not correct explanation of (A).
(c) (A) is correct bitt (R) is wrong.
(d) (A) is wrong but (R) is correct.
Answer:
(a) Both (A) and (R) are correct and (R) is the correct explanation of (A).

Samacheer Kalvi 11th Chemistry Environmental Chemistry 2 Mark Questions and Answers

Question 1.
What is meant by environmental pollution?
Answer:
Any undesirable change in our environment that have harmful effects on plants. animals and human beings is called environmental pollution.

Question 2.
Write a note on constituents of earth’s atmosphere.
Answer:
Earth’s atmosphere is a layer of gases retained by earth’s gravity. it contains roughly 78% Nitrogen, 21% Oxygen. 0.93% Argon, 0.04% Carbon dioxide. traces of other gases and little amount of water vapour. This mixture is commonly known as air.

Question 3.
What is called troposphere? How many layers are present in it? Give their names.
Answer:

1. The lowest layer of the atmosphere is called the troposphere and il extends from 0 10 km from the earth surface.
2. About 80% of the mass of the atmosphere is in this layer. 3 layers are present in it.
3. They are –
   • Hydrosphere
   • Lithosphere
   • Biosphere

Question 4.
Write about hydrosphere (or) Why Earth is called as Blue planer?
Answer:

• Hydrosphere include all types of water sources like oceans, seas, rivers, lakes. streams, underground water, polar ice-caps, clouds etc.
• It covers about 75% of the earth’s surface. Hence earth is called as Blue planet.

Question 5.
What is lithosphere?
Answer:
Lithosphere includes soil, rocks and mountains which are solid components of Earth.

Question 6.
What is biosphere?
Answer:
Biosphere includes the lithosphere. hydrosphere and atmosphere integrating the living organisms present in the lithosphere, hydrosphere and atmosphere.

Question 7.
What is air pollution?
Answer:
Air pollution is defined as any undesirable change in air which adversely affects living organisms. Air pollution is limited to troposphere and stratosphere.

Question 8.
What are the types of air pollutants? Give examples.
Answer:
1. Air pollutants exists in two major forms namely:
(a) Gaseous air pollutants
(b) Particulates

2. Gaseous air pollutants:
Oxides of sulphur, oxides of nitrogen, oxides of carbon and hydrocarbons are the gaseous air pollutants.

3. Particulate pollutants:
Particulate pollutants are small solid particles and liquid droplets suspended in air.
Exarnple:
dust, pollen, smoke, soot, aerosols.

Question 9.
Define greenhouse effect.
Answer:
Greenhouse effect is defined as the heating up of the earth’s surface due to trapping of infrared radiations reflected by earth’s surface by the CO₂ layer in the atmosphere.

Question 10.
What is Global warming?
Answer:
The heating up of the earth through the greenhouse effect is called Global warming.

Question 11.
When rain water is named as acid rain?
Answer:
Rain water normally has a pH of 5.6 due to dissolution of atmospheric CO₂ particles into it. Oxides of sulphur and nitrogen in the atmosphere are absorbed by droplets of water that make up clouds and get chemically converted into sulphuric acid and nitric acid. As a result the pH of rainwater drops below 5.6 and hence it is called acid rain.

Question 12.
What is stone leprosy? How is it formed?
Answer:

• The attack on the marble of buildings by acid rain is called stone leprosy.
• Acid rain causes extensive damage to buildings made up of marble CaCO + H₂SO₄ CaSO₄ + H₂O + CO₂↑

Question 13.
What are fumes? Give one example.
Answer:
Fumes are one of the non-viable particulate pollutants air. They are obtained by condensation of vapours released during sublimation, distillation, boiling and calcination. For example, organic solvents, metals and metallic oxides form fume particles.

Question 14.
What are the techniques to reduce particulate pollutants?
Answer:
The particulates from air can be removed by using electrostatic precipitators, gravity settling chambers, wet scrubbers or by cyclone collectors. These techniques are base on washing away or settling of the particulate matter.

Question 15.
How will you control photochemical smog?
Answer:
The formation of photochemical smog can be suppressed by preventing the release of nitrogen oxide and hydrocarbons into the atmosphere from the motor vehicles by using catalytic convertors in engines. Plantation of certain trees like Pinus, Pyrus Querus vitus and Juniparus can metabolise nitrogen oxide.

Question 16.
What is meant by water pollution’?
Answer:
Water pollution is defined as the addition of foreign substances or factors like heat which degrades the quality of water so that it becomes an health hazard or unfit for use.

Question 17.
What are the sources of water pollution? Give examples.
Answer:

• The water pollutants originate form both natural as well as human activities. The source of water pollution are classified as point and non-point sources.
• Easily identified source of water pollution is called a point source. For example, Municipal and industrial discharge pipes.
• Non-point source cannot be identified easily. For example, agricultural runoffs, mining wastes, acid rain, storm water drainage and construction sediments.

Question 18.
What is BOD’?
Answer:
The total amount of oxygen (in milligrams) consumed by microorganisms in decomposing the waste in one litre of water at 20°C for a period of 5 days is cal Led biochemical oxygen demand (BOD) and its value is expressed in ppm.

Question 19.
What is COD?
Answer:
Chemical oxygen demand (COD) is defined as the amount of oxygen required by the organic matter in a sample of water for its oxidation by a strong oxidising agent like K₂Cr₂O₇ in acidic medium for a period of 2 hours.

Question 20.
What are total dissolved solids (TDS)?
Answer:

• Most of the salts are soluble in water. It include cations like calcium, magnesium, sodium, potassium, iron and anions like carbonate, bicarbonate, chloride, sulphate, phosphate and nitrate.
• Use of drinking water having TDS (total dissolved solids) concentration higher than 500 ppm causes possibilities of irritation in stomach and intestine.

Question 21.
What are the constituents of soil?
Answer:
Soil is a thin layer of organic and inorganic material that covers the earth’s rocky surface. Soil constitutes the upper crust of the earth, which supports land, plants and animals.

Question 22.
Define – soil pollution.
Answer:
Soil pollution is defined as the build up of persistent toxic compounds, radioactive materials, chemical salts and disease causing agents in soil which have harmful effects on plant growth and animal health. Soil pollution affects the structure and fertility of soil, ground water quality and food chain in biological ecosystem.

Question 23.
Explain how industrial waste affects the soil.
Answer:

• Industrial activities have been the biggest contributor to soil pollution especially the mining and manufacturing activities.
• Industrial wastes include cyanides. chromates, acids, alkalis and metals like mercury, copper, zinc, cadmium and lead.
• These industrial wastes in the soil surface lies for a long time and makes it unsuitable for use.

Question 24.
What is green chemistry?
Answer:

• Efforts to control environment pollution have resulted in the development of chemicals favorable for environment and this branch of science is called green chemistry.
• It is a chemical philosophy encouraging the design of products and processes that reduces or eliminates the use and generation of hazardous substances.

Question 25.
Write a note about dry cleaning of clothes.
Answer:
Solvents like tetrachioroethylene is used in dry cleaning of clothes, pollute the ground water and are carcinogenic. In place of tetrachloroethylene liquefied CO₂ with suitable detergents an alternate solvent used. Liquefied CO₂ is not that much harmful for the groundwater. Nowadays H₂O₂ is used for bleaching clothes in laundry that give better results and utilises less water.

Question 26.
Carbon monoxide gas is more dangerous than carbon dioxide gas. Why?
Answer:
Carbon monoxide gas combines with haemoglobin to form a very stable compound known as carboxy haemoglobin. When its concentration in blood reaches 3-4%, the oxygen carrying capacity of the blood is greatly reduced. This results into headache, nervousness and sometimes death of the person. On the other hand CO₂ does not combine with haemoglobin and hence it is less harm ful than CO.

Question 27.
Which gases are responsible for greenhouse effect? List some of them.
Answer:
CO, is mainly responsible for greenhouse effect. Other greenhouse gases are methane, nitrous oxide, water vapours, CFCs and ozone.

Question 28.
A large number of fishes are suddenly found floating dead on a lake. There is no evidence of toxic dumping but you find an abundance of phytoplankton. Suggest a reason for the fish killing.
Answer:
Excessive phytoplankton (organic pollutants such as leaves, grass trash etc.) growth which is present in water is biodegradable. Bacteria decomposes this organic matter in water. During this process when large number of bacteria decomposes the organic matter, they consume the dissolved oxygen in water. When the level of dissolved oxygen falls below 6 ppm then the fishes cannot survive and they die.

Question 29.
How carbon monoxide acts as a poison for human beings’?
Answer:
Carbon monoxide is a poisonous gas because it combines with haemoglobin of RBC to form carboxyhaernoglobin as:
CO + Haemoglobin ⇌ Carboxyhaemoglobin
It inhibits the transport of oxygen to different pans of the body. Thus the body becomes oxygen-starved.

Question 30.
Give three examples in which the principles green chemistry has been applied.
Answer:

• In dry-cleaning, use of liquefied CO₂ in place of non-environment friendly tetrachioroethene (Cl₂C = CCl₂).
• Use of H₂O₂ in bleaching in place of chlorine.
• In the manufacture of chemicals like ethanal by using environment-friendly chemicals and conditions. ,

Samacheer Kalvi 11th Chemistry Environmental Chemistry 3 Marks Questions and Answers

Question 1.
Write about Bhopal gas tragedy.
Answer:

• On 3rd Decembers. 1984 at Bhopal city in India, by the early morning, an explosion at Union carbide pesticide plant released a cloud of toxic gas (Methyl isocyanate) CH₃NCO into the air.
• Since the gas is twice as heavy as air, it did not drift away but formed a blanket over the surrounding area.
• It attacked people’s lungs and affect their breathing staying there or in the nearby areas. Thousands of peopic died and lives of many were ruined. The lungs, brain, eyes, muscles as well as gastrointestinal, neurological and immune system of those people who survived were severely affected.

Question 2.
Explain how the oxides of sulphur pollute the atmospheric air. Give its haririful eflects.
Answer:

• Sulphur dioxide and sulphur trioxide are produced by burning sulphur containing fossil fuels and by roasting of suiphide ores.
• SO₂ is a poisonous gas for both animals and plants. SO₂ causes eye irritation, coughing and respiratory diseases like asthma, bronchitis.
• SO₂ is oxidised to more harmful SO₃ gas in the presence of particulate matter present in the polluted air:
  
  SO₂ combines with atmospheric water vapour to form H₂SO₄ which comes down along with rain in the form of acid rain:
• Acid rain causes stone leprosy. affect aquatic ecosystem, corrode water pipes and causes respiratory ailment in humans and animals.

Question 3.
How oxides of nitrogen are harmful?
Answer:
(i) Oxides of nitrogen are produced during high temperature combustion processes, by oxidation of nitrogen in air and it is formed the combustion of fuels such as coal, diesel and petrol.

(iii) The oxides of nitrogen are converted into nitric acid which comes down in the form of acid rain. They also form reddish brown haze in heay traffic.
(iv) Nitrogen dioxide potentially damage plant leaves and retard photosynthesis.
(v) NO₂ is a respiratory irritant and it can cause asthma and lung injury.

Question 4.
Explain how hydrocarbons pollute the atmospheric air.
Answer:

• The compounds composed of carbon and Hydrogen only are called hydrocarbons. They are mainly produced naturally and also by incomplete combustion of automobile fuels.
• They are potential cancer causing (carcinogenic) agents.
• For example polynuclear aromatic hydrocarbons (PAH) are carcinogenic, they cause irritation in eyes and mucous membranes.

Question 5.
Write flotes about great London smog.
Answer:

• The great smog of London (1952) was an instance of severe air pollution that affected the London from 5th December 9^th of December, 1952 and then dispersed quickly when the whether changed.
• It causes major disruption by reducing the visibility and even penetrating indoor areas.
• Government medical reports estimated that 4000 people had died as a direct result of smog and 100.000 were made ill by the smog effect on their respiratory tract.

Question 6.
What are the effects of classical smog?
Answer:

• Smog is primarily responsible for acid rain.
• Smog results in poor visibility and it affects air and road transport.
• It also causes bronchial irritation.

Question 7.
Explain how oxides of nitrogen are introduced directly into the stratosphere?
Answer:

• Nitrogen oxides are introduced directly into the stratosphere by the supersonic jet aircraft engines in the form of exhaust gases.
• These oxides arc released by combustion of fossil fuels and nitrogen fertilisers. Inert nitrous oxide in the stratosphere is photochemically converted into more reactive nitric oxide.
• Oxides of nitrogen catalyses the decomposition of ozone and are themselves regenerated. Ozone gets depleted as follows:
  
  Thus NO is regenerated in the chain reaction.

Question 8.
How chemical wastes pollute water?
Answer:

• A whole variety of chemicals from industries, such as metals and solvents are poisonous to fish and other aquatic life.
• Toxic pesticides can accumulate in fish and shell fish and poison the people who eat them.
• Detergents and oil float spoils the water bodies.
• Acids from mine drainage and salts from various sources can also contaminate water sources.

Question 9.
Explain the presence of fluoride in water and its hazardous effects?
Answer:

• Fluoride ion deficiency in drinking water causes tooth decay.
• The fluoride ions make the enamel on teeth much harder by converting hydroxyapatite
  [3(Ca₃(PO₄)₂. Ca(OFl)₂]. the enamel on the surface of the teeth into much harder fluorapatite [3(Ca₃(PO₃)₂. CaF₂]
• Fluoride ion concentration above 2 ppm causes brown mottling of teeth. Excess fluoride causes damage to bones and teeth.

Question 10.
Explain the harmful effects of

1. lead
2. Nitrate in drinking water.

Answer:

1. Drinking water containing lead contamination above 50 ppm can cause damage to liver, kidneys and reproductive system.
2. Use of drinking water having concentration of nitrates higher than 45 ppm may cause (blue baby syndrome) methemoglobinemia disease in chiidrens.

Question 11.
Explain how styrene is produced by traditional and greener routes?
Answer:
1. Traditional route:
This method involve two steps-Carcinogenic benzene reacts with ethylene to form ethyl benzene. After that ethyl benzene undergoes dehydrogenation using Fe₂O₃ / Al₂O₃ to give styrene.

2. Greener route:
To avoid carcinogenic benzene. greener routes to start with cheaper and
environment friendly xylene.

Question 12.
How acetaldehyde is commercially prepared by green chemistry?
Answer:
Acetaldehyde is commercially prepared by one step oxidation of ethene in the presence of ionic catalyst in aoiieniis medium with 9% yield.

Question 13.
What do you mean by ozone hole? What are its consequences?
Answer:
Depletion of ozone layer creates some sort of holes in the blanket of ozone which surrounds us in the atmosphere and this is known as ozone hole.

• With the depletion of the ozone layer, UV radiations filters into the troposphere which leads to ageing of skin. cataract, sunburn, skin cancer etc.
• By killing many of the phytoplanktons, it can damage the fish productivity.
• Evaporation rate increases through the surface and stomata of leaves which can decrease the moisture content of the soil.

Question 14.
What is photo chemical smog? What arc its effects? How can it be controlled?
Answer:
It is a kind of smog formed in warm, dry and sunny climate. It is formed when sunlight is absorbed by SO₂ oxides of nitrogen and hydrocarbons. It act as an oxidising agent.

Effects of photo chemical smog:

• It produces irritation in eyes and also in respiratory system.
• It can damage many materials such as metals, stones, building materials etc.
• NO₂ present in photochemical smog gives it brown colour which reduces the visibility.
• it is harmful to fabrics, crops and ornamental plants.

Control of photochemical smog:

• By using catalytic converters in automobilës.
• By spraying certain compounds into the atmosphere which generate free radicals that can easily combine with the free radicals that initiates the reaction forming toxic compounds of photochernical smog.
• Certain plants such as Pinus, Juniparus, Pyrus could be also helpful in this matter.

Question 15.
(a) Define eutrophication and pneumoconiosis.
(b) Write differences between photochemical smog and classical smog.
Answer:
(a) Eutrophication:
When the growth of algae increases in the surface of water, dissolved oxygen in water is greatly reduced. This phenomenon is known as eutrophication. Due to this growth of fishes gets inhibited.

(b) Pueumoconiosis:
It is a disease which irritates lungs. It causes scarring or fibrosis of the lungs.

Pholochemical smog:

• It is formed as a result of photochernical decomposition of nitrogen dioxide and chemical reactions involving hydrocarbons.
• It takes place during dry warm season in presence of sunlight.
• It is oxidising in nature.

Classical smog:

• It’s formed due to condensation of SO₂ vapours on particles of carbon in cold climate.
• it is generally formed during winter when there is severe cold.
• It is reducing in nature.

Samacheer Kalvi 11th Chemistry Environmental Chemistry 5 Marks Questions and Answers

Question 1.
Explain about the different layers of Earth’s atmosphere.
Answer:
Earth’s atmosphere can he divided into different layers with characteristic altitude and temperature.

Question 2.
What arc the health effects of particulate pollutants?
Answer:
1. Dust, mist, fumes etc. are air borne particles which are dangerous for human health. Particulate pollutants bigger than 5 microns are likely to settle in the nasal passage whereas particles of about 10 microns enter the lungs easily and causes scaring or fibrosis of lung lining.

They irritate the lungs and causes cancer and asthma. This disease is called pneumoconiosis. Coal miners may suffer from black lung disease. Textile workers may suffer from white lung disease.

2. Lead particulates affect children’s brain. interferes with maturation of RBC’s and even causes cancer.

3. Particulates in the atmosphere reduces the visibility by scattering and absorption of sun light. It is dangerous for aircraft and motor vehicles.

4. Particulates provide nuclei for cloud formation and increases fog and rain.

5. Particulates deposit on plant leaves and hinder the intake of CO₂ from the air and affect photosynthesis.

Question 3.
What arc the effects of photochernical smog?
Answer:

• The three main components of photochemical smog are nitrogen oxide, ozone and oxidized hydrocarbons like HCHO, CH₂ = CH – CRO and PAN.
• Photo chemical smog causes irritation to eyes. skin and lungs. It also increases the chance of asthma.
• high concentration of ozone and NO can cause nose and throat irritation, chest pain, difficulty in breathing.
• PAN is toxic to plants, attack younger leaves and cause bronzing and glazing of their surfaces.
• It causes corrosion of metals, stones, building materials and painted surfaces.

Question 4.
Explain about the environmental impacts of ozone depletion.
Answer:
1. The formation and destruction of ozone is a regular natural process, which never disturbs the equilibrium level of ozone in the stratosphere. Any change in the equilibrium level of ozone in the atmosphere will adversely affect the Life in biosphere in the following ways.
2. Depletion of ozone layer will allow more UV rays to reach the earth surface and would cause skin cancer and also decreases the immunity level in human beings.
3. UV radiations atlecis plant proteins which lead to harniful mutation in plant cells.
4. UV radiations affect the growth of phytoplankton and as a result ocean food chain is disturbed and it even damages the fish productivity.

Question 5.
Explain the list of major water pollutants and their sources.
Answer:

• Microorganisms – Domestic sewage, domestic waste water, dung heap
• Organic wastes – Domestic sewage, animal excreta, food processing factory wastc. detergents and decayed animals and plants
• Plant nutrients – Chemical fertilisers
• Heavy metals – Heavy metal producing factories
• Sediments – Soil erosion by agriculture and strip-mining
• Pesticides – Chemicals used for killing insects, fungi and weeds
• Radioactive substances – Mining of uranium containing minerals
• Heat – Water used for cooling in industries

Question 6.
Describe about the causes of water pollution.
Answer:
Causes of water pollution –
1. Microbiological pollutants:
(a) Disease causing microorganisms like bacteria, viruses and protozoa are most senous water pollutants. They come from domestic sewage and animal excreta.
(b) Fish and shellfish can become contaminated from them and people who eat them will also become ill.
(c) Dysentery and cholera are water borne diseases.
(d) Human excrcta contain bacteria such as Escherichia coll and Streptococcus farcical- -is which causes gastrointestinal diseases.

2. Organic wastes:
Organic matter such as leaves, grass, trash can also pollute water. Water pollution is cause by excessive phytoplankton growth within water.

3. Chemical wastes:
A whole variety of chemicals from industries such as metals and solvents are poisonous to fish and other aquatic life. Detergents and oils float spoils the water bodies. Acids from mine drainage and salts form various sources can also contaminate water sources.

Question 7.
What are the harmful effects of chemical water pollutants’?
Answer:

1. Cadmium and mercury can cause kidney damage.
2. Lead poisoning can lead to severe damage of kidneys. liver and brain. It also affects the central nervous system.
3. Polychiorinated biphenyl causes skin diseases and are carcinogenic in nature.

Question 8.
Explain about green chemistry in day-to-day life.
Answer:
1. Dry cleaning of clothes:
Solvents like tetrachloroethylene used in dry cleaning of clothes, pollute the ground water and are carcinogenic. In place of tetrachloro ethylene, liquefied CO₂ with suitable detergent is an alternate solvent used. Liquefied CO₂ is not harmful to the ground water. Nowadays H₂O₂ is used for bleaching clothes in laundry, gives better result and utilises less water.

2. Bleaching of paper:
Conventional method of bleaching was done with chlorine. Nowadays H₂O₂ can be used for bleaching paper in the presence of catalyst.

3. Synthesis of chemicals:
Acetaldehyde is commercially prepared by one step oxidation of ethene in the presence of ionic catalyst in aqueous medium with 90% yield.

4. Instead of petrol, methanol is used as a fuel in automobiles.
5. Neem based pesticides have been synthesis-ed, which are more safer than the chlorinated hydrocarbons.

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 6 Trigonometry Ex 6.1

9th standard trigonometry exercise 6.1 Question 1.
From the given figure find all the trigonometric ratios of angle B.
Solution:

9th maths trigonometry exercise 6.1 Question 2.
From the given figure, find the values of
(i) sin B
(ii) sec B
(iii) cot B
(iv) cos C
(v) tan C
(vi) cosec C
Solution:

trigonometry exercise 6.1 Question 3.
If 2 cos θ = \(\sqrt{3}\), then find all the trigonometric ratios of angle θ.
Solution:

Trigonometry solutions exercise 6.1 Question 4.
If cos A = \(\frac{3}{5}\), then find the value of \(\frac{\sin A-\cos A}{2 \tan A}\)
Solution:

trignometry solution of 9th class Question 5.
If cos A = \(\frac{2 x}{1+x^{2}}\) then find the values of sin A and tan A in terms of x.
Solution:

Question 6.

Solution:

Question 7.
If 3 cot A = 2, then find the value of \(\frac{4 \sin A-3 \cos A}{2 \sin A+3 \cos A}\)
Solution:

Question 8.
If cos θ : sin θ = 1 : 2, then find the value of \(\frac{8 \cos \theta-2 \sin \theta}{4 \cos \theta+2 \sin \theta}\)
Solution:

Question 9.
From the given figure, prove that θ + ϕ = 90°. Also prove that there are two other right angled triangles. Find sin α, cos β and tan ϕ
Solution:


(∴ By Pythagoras theorem, in a right angled triangle square of hypotenuse is equal to sum of the squares of other two side)
And also in the figure, ∆ADC, ∆DBC are two other triangles.
As per the data given,
9²+ 12² = 81 + 144 = 225 = 15²
∴ ∆ ADC is a right angled triangle, then 12² + 16² = 144 + 256 = 400 = 20²
∴ ∆ DBC is also a right angled triangle

Question 10.
A boy standing at point O finds his kite flying at a point P with distance OP = 25 m. It is at a height of 5 m from the ground. When the thread is extended by 10 m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)
Solution:
In the figure,
∆OPM, ∆OQN are similar triangles. In similar triangles the sides are in the same proportional.

Students can Download Economics Chapter 7 International Economics Questions and Answers, Notes Pdf, Samacheer Kalvi 12th Economics Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 7 International Economics

Samacheer Kalvi 12th Economics International Economics Text Book Back Questions and Answers

Part – A
Multiple Choice Questions.

Question 1.
Trade between two countries is known as ………………………. trade
(a) External
(b) Internal
(c) Inter – regional
(d) Home
Answer:
(a) External

Question 2.
Which of the following factors influence trade?
(a) The stage of development of a product
(b) The relative price of factors of productions
(c) Government
(d) All of the above.
Answer:
(d) All of the above.

Question 3.
International trade differs from domestic trade because of ……………………….
(a) Trade restrictions
(b) Immobility of factors
(c) Different government policies
(d) All the above
Answer:
(d) All the above

Question 4.
In general, a primary reason why nations conduct international trade is because ……………………….
(a) Some nations prefer to produce one thing while others produce another
(b) Resources are not equally distributed among all trading nations
(c) Trade enhances opportunities to accumulate profits
(d) Interest rates are not identical in all trading nations
Answer:
(b) Resources are not equally distributed among all trading nations

Question 5.
Which of the following is a modem theory of international trade?
(a) Absolute cost
(b) Comparative cost
(c) Factor endowment theory
(d) None of these
Answer:
(c) Factor endowment theory

Question 6.
Exchange rates are determined in ……………………….
(a) Money market
(b) Foreign exchange market
(c) Stock market
(d) Capital market
Answer:
(b) Foreign exchange market

Question 7.
Exchange rate for currencies is determined by supply and demand under the system of ……………………….
(a) Fixed exchange rate
(b) Flexible exchange rate
(c) Constant
(d) Government regulated
Answer:
(b) Flexible exchange rate

Question 8.
Net export equals ……………………….
(a) Export × Import
(b) Export + Import
(c) Export – Import
(d) Exports of services only
Answer:
(c) Export – Import

Question 9.
Who among the following enunciated the concept of single factoral terms of trade?
(a) Jacob Viner
(b) G.S.Donens
(c) Taussig
(d) J.S.Mill
Answer:
(a) Jacob Viner

Question 10.
Terms of Trade of a country show ……………………….
(a) Ratio of goods exported and imported
(b) Ratio of import duties
(c) Ratio of prices of exports and imports
(d) Both (a) and (c)
Answer:
(c) Ratio of prices of exports and imports

Question 11.
Favourable trade means value of exports are ………………………. Than that of imports.
(a) More
(b) Less
(c) More or Less
(d) Not more than
Answer:
(a) More

Question 12.
If there is an imbalance in the trade balance (more imports than exports), it can be reduced by ……………………….
(a) Decreasing customs duties
(b) Increasing export duties
(c) Stimulating exports
(d) Stimulating imports
Answer:
(c) Stimulating exports

Question 13.
BOP includes ……………………….
(a) Visible items only
(b) Invisible items only
(c) Both visible and invisible items
(d) Merchandise trade only
Answer:
(c) Both visible and invisible items

Question 14.
Components of balance of payments of a country includes ……………………….
(a) Current account
(b) Official account
(c) Capital account
(d) All of above
Answer:
(d) All of above

Question 15.
In the case of BOT ……………………….
(a) Transactions of goods are recorded.
(b) Transactions of both goods and services are recorded.
(c) Both capital and financial accounts are included.
(d) All of these
Answer:
(a) Transactions of goods are recorded.

Question 16.
Tourism and travel are classified in which of balance of payments accounts?
(a) Merchandise trade account
(b) Services account
(c) Unilateral transfers account
(d) Capital account
Answer:
(b) Services account

Question 17.
Cyclical disequilibrium in BOP occurs because of ……………………….
(a) Different paths of business cycle.
(b) The income elasticity of demand or price elasticity of demand is different.
(c) Long – run changes in an economy
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)

Question 18.
Which of the following is not an example of foreign direct investment?
(a) The construction of a new auto assembly plant overseas
(b) The acquisition of an existing steel mill overseas
(c) The purchase of bonds or stock issued by a textile company overseas
(d) The creation of a wholly owned business firm overseas
Answer:
(c) The purchase of bonds or stock issued by a textile company overseas

Question 19.
Foreign direct investments not permitted in India ……………………….
(a) Banking
(b) Automic energy
(c) Pharmaceutical
(d) Insurance
Answer:
(b) Automic energy

Question 20.
Benefits of FDI include, theoretically ……………………….
(a) Boost in Economic Growth
(b) Increase in the import and export of goods and services
(c) Increased employment and skill levels
(d) All of these
Answer:
(d) All of these

Part – B
Answer The Following Questions Each Question Carries 2 Marks.

Question 21.
What is International Economics?
Answer:

1. International Economics is that branch of economics which is concerned with the exchange of goods and services between two or more countries. Hence the subject matter is mainly related to foreign trade.
2. International Economics is a specialized field of Economics which deals with the economic interdependence among countries and studies the effects of such interdependence and the factors that affect it.

Question 22.
Define international trade?
Answer:
International Trade refers to the trade or exchange of goods and services between two or more countries. In other words, it is a trade among different countries or trade across political boundaries. It is also called as ‘external trade’ or ‘foreign trade’ or ‘inter-regional trade’.

Question 23.
State any two merits of trade?
Answer:

1. Trade is one of the powerful forces of economic integration.
2. The term ‘trade’ means exchange of goods, wares or merchandise among people.

Question 24.
What is the main difference between Adam Smith and Ricardo with regard to the emergence of foreign trade?
Answer:
Adam Smith Foreign Trade:

1. According to Adam Smith the basis of International trade was absolute cost advantage.
2. Trade between two countries would be mutually beneficial when one country produces a commodity at an absolute cost advantage.
3. Adam Smith argued that all nations can be benefitted when there is free trade and specialisation interms of their absolute cost advantage.

Ricardo Foreign Trade:

1. Ricardo demonstrates that the basis of trade is the comparative cost difference.
2. Trade can take place even if the absolute cost difference is absent but there is comparative cost difference.
3. According to Ricardo a country can gain from trade when it produces at relatively lower costs.

Question 25.
Define Terms of Trade?
Answer:
Terms of Trade:

1. The gains from international trade depend upon the terms of trade which refers to the ratio of export prices to import prices.
2. It is the rate at which the goods of one country are exchanged for goods of another country’.
3. It is expressed as the relation between export prices and import prices.
4. Terms of trade improves when average price of exports is higher than average price of imports.

Question 26.
What do you mean by balance of payments?
Answer:
Balance of Payments (BOP):

1. BoP is a systematic record of a country’s economic and financial transactions with the rest of the world over a period of time.

2. When a payment is received from a foreign country, it is a credit transaction while a payment to a foreign country is a debit transaction.

3. The principal items shown on the credit side are exports of goods and services, transfer receipts in the form of gift etc., from foreigners, borrowing from abroad, foreign direct investment and official sale of reserve assets including gold to foreign countries and international agencies.

4. The principal items on the debit side include imports of goods and serv ices, transfer payments to foreigners, lending to foreign countries, investments by residents in foreign countries and official purchase of reserve assets or gold from foreign countries and international agencies.

Question 27.
What is meant by Exchange Rate?
Meaning of Foreign Exchange (FOREX):

1. FOREX refers to foreign currencies. The mechanism through which payments are effected between two countries having different currency systems is called FOREX system. It covers methods of payment, rules and regulations of payment and the institutions facilitating such payments.

2. “FOREX is the system or process of converting one national currency into another, and of transferring money from one country to another”.

Part – C
Answer The Following Questions Each Question Carries 3 Marks.

Question 28.
Describe the subject matter of International Economics?
Answer:
Subject Matter of International Economics:
The subject matter of International Economics includes large number of segments which are classified into the following parts.

1. Pure Theory of Trade:
This component explains the causes for foreign trade, composition, direction and volume of trade, determination of the terms of trade and exchange rate, issues related to balance of trade and balance of payments.

2. Policy Issues:
Under this part, policy issues such as free trade vs. protection, methods of regulating trade, capital and technology flows, use of taxation, subsidies and dumping, exchange control and convertibility, foreign aid, external borrowings and foreign direct investment, measures of correcting disequilibrium in the balance of payments etc are covered.

3. International Cartels and Trade Blocs:
This part deals with the economic integration in the form of international cartels, customs unions, monetary unions, trade blocs, economic unions and the like. It also discusses the operation of Multi National Corporations (MNCs).

4. International Financial and Trade Regulatory Institutions:
The financial institutions like International Monetary Fund IMF, IBRD, WTO etc which influence international economic transactions and relations shall also be the part of international economics.

Question 29.
Compare the Classical Theory of international trade with Modern Theory of International trade?
Answer:
Classical Theory of International Trade:

1. The classical theory explains the phenomenon of international trade on the basis of labour theory of value.
2. It presents a one factor (labour) model.
3. It attributes the differences in the comparative costs to differences in the productive efficiency of workers in the two countries.

Modern Theory of International Trade:

1. The modem theory explains the phenomenon of international trade on the basis of general theory of value.
2. It presents a multi – factor (labour and capital) model.
3. It attributes the differences in comparative costs to the differences in factor endowments in the two countries.

Question 30.
Explain the Net Barter Terms of Trade and Gross Barter Terms of Trade?
Answer:
1. Net Barter Terms of Trade:
This type was developed by Taussig in 1927.The ratio between the prices of exports and of imports is called the “net barter terms of trade’. It is named by Viner as the ‘commodity terms of trade’.
It is expressed as:
T_n = (P _x /P_m ) × 100
Where,
T_n = Net Barter Terms of Trade
P_x = Index number of export prices
P_m = Index number of import prices
This is used to measure the gain from international trade. If ‘Tn’ is greater than 100, then it is a favourable terms of trade which will mean that for a rupee of export, more of imports can be received by a country.

2. Gross Barter Terms of Trade:
This was developed by Taussig in 1927 as an improvement over the net terms of trade. It is an index of relationship between total physical quantity of imports and the total physical quantity of exports.
T = (Q_m/Q_x) × 100
Where,
Q_m = Index of import quantities
Q_x = Index of export quantities
If for a given quantity of export, more quantity of import can be consumed by a country, then one can say that terms of trade are favourable.

Question 31.
Distinguish between Balance of Trade and Balance of Payments?
Answer:
Balance of Trade:

1. Balance of Trade refers to the total value of a country’s exports of commodities and total value of imports of commodities.
2. Only export and import of commodities are included in the statement of Balance of Trade of a country.
3. The Balance of Trade between the values of goods exchanged between two countries.
4. Balance of Trade is a merchandise items or visible items only.

Balance of Payments:

1. Balance of payments is a systematic record of a country’s economic and financial transactions with the rest of the world over a period of time.
2. The principal items shown on the credit side are exports of goods and services, transfer receipts in the form of gift, etc.
3. The Balance of payments between the values of goods and services changed between two countries.
4. Balance of payments is a both visible and non – visible items.

Question 32.
What are import quotas?
Answer:
Import Control: Imports may be controlled by

1. Imposing or enhancing import duties
2. Restricting imports through import quotas
3. Licensing and even prohibiting altogether the import of certain non-essential items. But this would encourage smuggling.

Question 33.
Write a brief note on flexible exchange rate?
Answer:
Flexible Exchange Rates: Under the flexible exchange rate (also known as floating exchange rate) system, exchange rates are freely determined in an open market by market forces of
demand and supply

Question 34.
State the objectives of Foreign Direct Investment.
Answer:
Objectives of FDI:
FDI has the following objectives.

1. Sales Expansion
2. Acquisition of resources
3. Diversification
4. Minimization of competitive risk.
   • FDI may help to increase the investment level and thereby the income and employment in the host country.
   • Direct foreign investment may facilitate transfer of technology to the recipient country.
   • FDI may also bring revenue to the government of host country when it taxes profits of foreign firms or gets royalties from concession agreements.
   • A part of profit from direct foreign investment may be ploughed back into the expansion, modernization or development of related industries.
   • It may kindle a managerial revolution in the recipient country through professional management and sophisticated management techniques.
   • Foreign capital may enable the country to increase its exports and reduce import requirements. And thereby ease BoP disequilibrium.
   • Foreign investment may also help increase competition and break domestic monopolies.
   • If FDI adds more value to output in the recipient country than the return on capital from foreign investment, then the social returns are greater than the private returns on foreign investment.
   • By bringing capital and foreign exchange FDI may help in filling the savings gap and the foreign exchange gap in order to achieve the goal of national economic development.
   • Foreign investments may stimulate domestic enterprise to invest in ancillary industries in collaboration with foreign enterprises.

Part – D
Answer The Following Questions Each Question Carries 5 Marks.

Question 35.
Discuss the differences between Internal Trade and International Trade?
Answer:
Internal Trade:

1. Trade takes place between different individuals and firms within the same nation.
2. Labour and capital move freely from one region to another.
3. There will be free flow of goods and services since there are no restrictions.
4. There is only one common currency.
5. The physical and geographical conditions of a country are more or less similar.
6. Trade and financial regulations are more or less the same.
7. There is no difference in political affiliations, customs and habits of the people and government policies.

International Trade:

1. Trade takes place between different individuals and firms in different countries.
2. Labour and capital do not move easily from one nation to another.
3. Goods and services do not easily move from one country to another since there are a number of restrictions like tariff and quota.
4. There are different currencies.
5. There are differences in physical and geographical conditions of the two countries.
6. Trade and financial regulations such as interest rate, trade laws differ between countries.
7. Differences are pronounced in political affiliations, habits and customs of the people and government policies

Question 36.
Explain briefly the Comparative Cost Theory?
Answer:
Ricardo’s Theory of Comparative Cost Advantage:

1. David Ricardo, the British economist in his ‘Principles of Political Economy and Taxation’ published in 1817, formulated a systematic theory called ‘Comparative Cost Theory’.

2. Ricardo demonstrates that the basis of trade is the comparative cost difference. In other words, trade can take place even if the absolute cost difference is absent but there is comparative cost difference.

3. According to Ricardo, a country can gain from trade when it produces at relatively lower costs. Even when a country enjoys absolute advantage in both goods, the country would specialize in the production and export of those goods which are relatively more advantageous.

Assumptions:

1. There are only two nations and two commodities (2 × 2 model)
2. Labour is the only element of cost of production.
3. All labourers are of equal efficiency.
4. Labour is perfectly mobile within the country but perfectly immobile between countries, (v) Production is subject
5. To the law of constant returns.
6. Foreign trade is free from all barriers.
7. No change in technology.
8. No transport cost.
9. Perfect competition.
10. Full employment.
11. No government intervention.

Illustration:
Ricardo’s theory of comparative cost can be explained with a hypothetical example of production costs of cloth and wheat in America and India.

It is evident from the example that India has an absolute advantage in production of both cloth and wheat.

However, India should concentrate on the production of wheat in which she enjoys a comparative cost advantage. (80/120 < 90/100). For America the comparative cost disadvantage is lesser in cloth production. Hence America will specialize in the production of cloth and export it to India in exchange for wheat. (Any exchange ratio between 0.88 units and 1.2 units of cloth against one unit of wheat represents gain for both the nations).

With trade, India can get 1 unit of cloth and 1 unit of wheat by using its 160 labour units. In the absence of trade, for getting this benefit, India will have to use 170 units of labour. America also gains from this trade. With trade, America can get 1 unit of cloth and one unit of wheat by using its 200 units of labour. Otherwise, America will have to use 220 units of labour for getting 1 unit of cloth and 1 unit of wheat.

Question 37.
Discuss the Modern Theory of International Trade?
Answer:
Modern Theory of International Trade:
Introduction:
The modem theory of international trade was developed by Swedish economist Eli Heckscher and his student Bertil Ohlin in 1919. This model was based on the Ricardian theory of international trade. This theory says that the basis for international trade is the difference in factor endowments. It is otherwise called as ‘Factor Endowment Theory’.

The Theory:
The classical theory argued that the basis for foreign trade was comparative cost difference and it considered only labour factor. But the modem theory of international trade explains the causes for such comparative cost difference. This theory attributes international differences in comparative costs to:

1. Difference in the endowments of factors of production between countries, and
2. Differences in the factor proportions required in production.

Assumptions:

1. There are two countries, two commodities and two factors. (2 × 2 × 2 model)
2. Countries differ in factor endowments.
3. Commodities are categorized in terms of factor intensity.
4. Countries use same production technology.
5. Countries have identical demand conditions.
6. There is perfect competition in both product and factor markets in both the countries

Explanation:
According to Heckscher – Ohlin, “a capital – abundant country will export the capital – intensive goods, while the labour-abundant country will export the labour – intensive goods”. A factor is regarded abundant or scare in relation to the quantum of other factors. A country can be regarded as richly endowed with capital only if the ratio of capital to other factors is higher than other countries

Illustration:

In the above example, even though India has more capital in absolute terms, America is more richly endowed with capital because the ratio of capital in India is 0.8 which is less than that in America where it is 1.25. The following diagram illustrates the pattern of word trade.

Limitations:

1. Factor endowment of a country may change over time.
2. The efficiency of the same factor (say labour) may differ in the two countries. For example, America may be labour scarce in terms of number of workers. But in terms of efficiency, the total labour may be larger.

Question 38.
Explain the types of Terms of Trade given by Viner?
Answer:
Terms of Trade related to the Interchange between Productive Resources:

1. The Single Factoral Terms of Trade:
Viner has devised another concept called “the single factoral terms of trade” as an improvement upon the commodity terms of trade. It represents the ratio of export – price index to the import – price index adjusted for changes in the productivity of a country’s factors in the production of exports. Symbolically, it can be stated as
T_f = (P_x / P_m ) F_x
Where, T_f stands for single factoral terms of trade index. F_x stands for productivity in exports (which is measured as the index of cost in terms of quantity of factors of production used per unit of export).

2. Double Factoral Terms of Trade:
Viner constructed another index called “Double factoral terms of Trade”. It is expressed as
T_ff = (P_x / P_m )(F_x / F_m)
which takes into account the productivity in country’s exports, as well as the productivity of foreign factors.
Here, F_m represents import index (which is measured as the index of cost in terms of quantity of factors of production employed per unit of imports).

Question 39.
Bring out the components of balance of payments account?
Answer:
Components of BOPs:
The credit and debit items are shown vertically in the BOP account of a country. Horizontally, they are divided into three categories, i.e.

1. The current account,
2. The capital account and
3. The official settlements account or official reserve assets account.

1. The Current Account:
It includes all international trade transactions of goods and services, international service transactions (i.e. tourism, transportation and royalty fees) and international unilateral transfers (i.e. gifts and foreign aid).

2. The Capital Account:
Financial transactions consisting of direct investment and purchases of interest-bearing financial instruments, non-interest bearing demand deposits and gold fall under the capital account.

3. The Official Reserve Assets Account:
Official reserve transactions consist of movements of international reserves by governments and dfficial agencies to accommodate imbalances arising from the current and capital accounts.

The official reserve assets of a country include its gold stock, holdings of its convertible foreign currencies and Special Drawing Rights (SDRs) and its net position in the International Monetary Fund (IMF).
Balance of payment (BOP) Account Chart
Credit (Receipts) – Debit (Payments) = Balance [Deficit (-), Surplus (+)]
Deficit if Debit > Credit

Question 40.
Discuss the various types of disequilibrium in the balance of payments?
Answer:
Types BOP Disequilibrium:
There are three main types of BOP Disequilibrium, which are discussed below.

1. Cyclical Disequilibrium,
2. Secular Disequilibrium,
3. Structural Disequilibrium.

1. Cyclical Disequilibrium:
Cyclical disequilibrium occurs because of two reasons. First, two countries may be passing through different phases of business cycle. Secondly, the elasticities of demand may differ between countries.

2. Secular Disequilibrium:
The secular or long-run disequilibrium in BOP occurs because of long – run and deep seated changes in an economy as it advances from one stage of growth to another. In the initial stages of development, domestic investment exceeds domestic savings and imports exceed exports, as it happens in India since 1951.

3. Structural Disequilibrium:
Structural changes in the economy may also cause balance of payments disequilibrium. Such structural changes include development of alternative sources of supply, development of better substitutes, exhaustion of productive resources or changes in transport routes and costs.

Question 41.
How the Rate of Exchange is determined? Illustrate?
Answer:
Determinants of Exchange Rates:
Exchange rates are determined by numerous factors and they are related to the trading relationship between two countries.
Factors determining Exchange Rate:

1. Differentials in Inflation
2. Differential in Interest Rates
3. Current Account Deficits
4. Public Debt
5. Terms of Trade
6. Political and Economic Stability
7. Recession
8. Speculation

1. Differentials in Inflation:

1. Inflation and exchange rates are inversely related.
2. A country with a consistently lower inflation rate exhibits a rising currency value, as its purchasing power increases relative to other currencies.

2. Differentials in Interest Rates:

1. There is a high degree of correlation between interest rates, inflation and exchange rates.
2. Central banks can influence over both inflation and exchange rates by manipulating interest rates.
3. Higher interest rates attract foreign capital and cause the exchange rate to rise and vice versa.

3. Current Account Deficits:

1. A deficit in the current account implies excess of payments over receipts.
2. The country resorts to borrowing capital from foreign sources to make up the deficit.
3. Excess demand for foreign currency lowers a country’s exchange rate.

4. Public Debt:

1. Large public debts are driving out foreign investors, because it leads to inflation.
2. As a result, exchange rate will be lower.

5. Terms of Trade:

1. A country’s terms of trade also determines the exchange rate.
2. If the price of a country’s exports rises by a greater rate than that of its imports, its terms ‘ of trade will improve.
3. Favorable terms of trade imply greater demand for the country’s exports and thus BoP becomes favorable.

6. Political and Economic Stability:
If a nation’s political climate is stable and economic performance is good, its currency value will be appreciated by attracting more foreign capital.

7. Recession:

1. Interest rates are low during the recession phase.
2. This will decrease inflow of foreign capital.
3. As a result, a currency will be depreciated against other currencies, thereby lowering the exchange rate.

8. Speculation:

1. If a country’s currency value is expected to rise, investors will demand more of that currency in order to make a profit in the near future.
2. This results in appreciation of the exchange rate.
3. Beside the above determinants, relative dominance in the global politics and the power to announce economic sanctions over other countries also determine exchange rates.

Question 42.
Explain the relationship between Foreign Direct Investment and economic development?
Answer:
Foreign Direct Investment (FDI) and Trade:

1. FDI is an important factor in global economy.
2. Foreign trade and FDI are closely related. In developing countries like India
3. FDI in the natural resource sector, including plantations, increases trade volume.
4. Foreign production by FDI is useful to substitute foreign trade.
5. FDI is also influenced by the income generated from the trade and regional integration schemes.
6. FDI is helpful to accelerate the economic growth by facilitating essential imports needed for carrying out development programmes like capital goods, technical know-how, raw materials and other inputs and even scarce consumer goods.
7. FDI may be required to fill the trade gap.
8. FDI is encouraged by the factors such as foreign exchange shortage, desire to create employment and acceleration of the pace of economic development.
9. Many developing countries strongly prefer foreign investment to imports.
10. However, the real impact of FDI on different sections of an economy.

Samacheer Kalvi 12th Economics International Economics Addtional Questions and Answers

Part – I
Multiple Choice Questions.

Question 1.
Foreign trade means ………………………..
(a) Trade between nations of the world
(b) Trade among different states
(c) Trade among two states
(d) Trade with one nation
Answer:
(a) Trade between nations of the world

Question 2.
Balance of Trade means
(a) Import and export of invisible items only
(b) Import and export of both visible and invisible items
(c) Import of visible items only
(d) Import and export of visible items only
Answer:
(d) Import and export of visible items only

Question 3.
International trade is regulated at present by ………………………..
(a) IBRD
(b) WTO
(c) OMF
(d) GATT
Answer:
(b) WTO

Question 4.
The exports of India are broadly classified into ……………………….. categories.
(a) Two
(b) Three
(c) Four
(d) Five
Answer:
(c) Four

Question 5.
The New Export – Import policy gives a further push to ………………………..
(a) Liberalisation
(b) Mixed system
(c) Capitalism
(d) Socialism
Answer:
(a) Liberalisation

Question 6.
The World Trade organisation is a ………………………..
(a) Promote of private foreign investment
(b) Promoter of International monetary co-operation
(c) Lateral trade agreement
(d) New trade body to settle trade disputes between nations
Answer:
(d) New trade body to settle trade disputes between nations

Question 7.
To promote ……………………….. stability is one of the aims of IMF.
(a) Exchange
(b) Money
(c) Investment
(d) Finance
Answer:
(a) Exchange

Question 8.
The New Export Import policy was implemented in ………………………..
(a) 1990 – 1995
(b) 1991 – 1996
(c) 1992 – 1997
(d) 1993 – 1998
Answer:
(c) 1992 – 1997

Question 9.
The role of WTO is to regulate trade among the nations of the ………………………..
(a) Trade
(b) Organisation
(c) World
(d) Regulation
Answer:
(c) World

Question 10.
The WTO was setup in the year ………………………..
(a) 1995
(b)1885
(c) 1875
(d) 1865
Answer:
(a) 1995

Question 11.
……………………….. means value of imports is in excess of the value exports.
(a) Balance of Trade
(b) Unfavourable balance of trade
(c) Favourable balance of trade
(d) Export trade
Answer:
(b) Unfavourable balance of trade

Question 12.
……………………….. items means the imports and exports of services and other foreign transfer transactions.
(a) Invisible
(b) Visible
(c) Exports
(d) Imports
Answer:
(a) Invisible

Question 13.
Foreign trade increases worker’s welfare atleast ……………………….. ways.
(a) Two
(b) Three
(c) Four
(d) Five
Answer:
(c) Four

Question 14.
……………………….. trade refers to the trade or exchange of goods and services between two or more countries.
(a) Internal
(b) External
(c) International
(d) Domestic
Answer:
(c) International

Question 15.
If trade is done on large scale it is called ………………………..
(a) Whole sale trade
(b) State trade
(c) Central trade
(d) World trade
Answer:
(a) Whole sale trade

Question 16.
The relationship between value of exports and value of imports is known as ………………………..
(a) EXIM
(b) Foreign exchange
(c) Trade
(d) Terms of trade
Answer:
(d) Terms of trade

Question 17.
If the value of exports is greater than value of imports then it is known as ……………………….. terms of trade.
(a) Unfavourable
(b) Favourable
(c) Moderate
(d) Low
Answer:
(b) Favourable

Question 18.
Imports of India may be divided into ……………………….. parts.
(a) Two
(b) Three
(c) Four
(d) Five
Answer:
(b) Three

Question 19.
……………………….. means imports and exports of commodities.
(a) EXIM
(b) Visible items
(c) Non visible items
(d) Foreign exchange
Answer:
(b) Visible items

Question 20.
……………………….. means exports and imports may be exactly equal.
(a) Balance of trade
(b) Balance of payments
(c) Balanced balance of Trade
(d) Balanced balance of payments
Answer:
(c) Balanced balance of Trade

Question 21.
A special branch of Economics which primarily deals with the basics of ……………………….. trade.
(a) Internal
(b) External
(c) International
(d) Foreign trade
Answer:
(c) International

Question 22.
FDI objective is called ………………………..
(a) Sales expansion
(b) Export expansion
(c) Import expansion
(d) EXIM expansion
Answer:
(a) Sales expansion

Question 23.
The currency of another country is called ………………………..
(a) Money transfer
(b) Money exchange
(c) Foreign exchange
(d) Foreign transfer
Answer:
(c) Foreign exchange

Question 24.
Abundance in the availability of a factor in a country is called ………………………..
(a) Endowment policy
(b) Comparative cost
(c) Absolute cost
(d) Factor Endowment
Answer:
(d) Factor Endowment

Question 25.
Foreign Investment mostly takes the form of ………………………..
(a) Indirect investment
(b) Direct investment
(c) IMF investment
(d) World bank investment
Answer:
(b) Direct investment

II. Match the following and choose the correct answer by using codes given below:

Question 1.
A. Internal Trade – (i) International trade
B. Modem Theory – (ii) Labour
C. Classical Theory – (iii) Geographical boundaries
D. Modem Theory – (iv) Eli Heckscher
Codes:
(a) A (ii) B (iii) C (iv) D (i )
(b) A (iii) B (i) C (ii) D (iv)
(c) A (iv) B (ii) C (i) D (iii)
(d) A (i) B (iv) C (iii) D (ii)
Answer:
(b) A (iii) B (i) C (ii) D (iv)

Question 2.
A. Export – (i) Disequillibrium
B. Secular – (ii) Surplus goods
C. Delibrate measure – (iii) Foreign loans
D. Monetary measures – (iv) Exchange control
Codes:
(a) A (ii) B (i) C (iii) D (iv)
(b) A (i) B (ii) C (iv) D (iii)
(c) A (iii) B (iv) C (ii) D (i)
(d) A (iv) B (iii) C (i) D (ii)
Answer:
(a) A (ii) B (i) C (iii) D (iv)

Question 3.
A. Adam Smith – (i) Foreign Exchange
B. Eli Heckscher – (ii) Absolute cost advantage
C. Movement of goods – (iii) Modem theory of International trade
D. FOREX – (iv) Visible trade
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iii) C (iv) D (i)
(c) A (iv) B (i) C (ii) D (iii)
(d) A (iii) B (iv) C (i) D (ii)
Answer:
(b) A (ii) B (iii) C (iv) D (i)

Question 4.
A. Term of trade – (i) Official reserve
B. FDI – (ii) Exchange rate
C. Gold stock – (iii) Income terms of trade
D. G.S; Dorrance – (iv) Global economy
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iv) B (iii) C (ii) D (i)
(c) A (ii) B (iv) C (i) D (iii)
(d) A (iii) B (i) C (iv) D (ii)
Answer:
(c) A (ii) B (iv) C (i) D (iii)

Question 5.
A. Net Barter Terms of Trade – (i) T_f = (P_x / P_m)F_s
B. Gross Barter Terms of Trade – (ii) T_n = (P_s / P_m) × 100
C. Income Terms of Trade – (iii) T_g = (Q_m / Q_s) × 100
D. Single Factoral Terms of Trade – (iv) T_s = (P_s / P_m)Q_s
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iv) B (iv) C (i) D (ii)
(c) A (iv) B (i) C (ii) D (iii)
(d) A (ii) B (iii) C (iv) D (i)
Answer:
(d) A (ii) B (iii) C (iv) D (i)

III. State whether the statements are true or false.

Question 1.
(i) Trade is one of the powerful forces of economic integration.
(ii) Price of a commodity is measured by the amount of labour required to produce it.

(a) Both (i) and (ii) are false
(b) Both (i) and (ii) are true
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(b) Both (i) and (ii) are true

Question 2.
(i) International Economics is a specialized field of economics.
(ii) Inflation and exchange rates are direct relationship.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is false but (ii) is true
(d) (i) is true but (ii) is false .
Answer:
(d) (i) is true but (ii) is false.

Question 3.
(i) Movement of goods are called “Visible Trade”.
(ii) Only export and import of commodities are included in the statement of balance of trade of the country.

(a) Both (i) and (ii) are false
(b) Both (i) and (ii) are true
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(b) Both (i) and (ii) are true

Question 4.
(i) The Income terms of trade was given by Taussig.
(ii) Gross Barter Terms of trade was developed by G.S. Dorrance.

(a) Both (i) and (ii) are false
(b) Both (i) and (ii) are true
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are false

Question 5.
(i) Viner constructed another index called “Double Factoral terms of Trade”.
(ii) Viner has devised another concept called the “Single factoral terms of trade”.

(a) Both (i) and (ii) are false
(b) Both (i) and (ii) are true
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(b) Both (i) and (ii) are true

IV. Which of the following is correctly matched.

Question 1.
(a) David Ricardo – Factor Endowment Theory
(b) Eli Heckscher – British Economist
(c) Marshall – Swedish Economist
(d) Adam Smith – Theory of Absolute cost advantage
Answer:
(d) Adam Smith – Theory of Absolute cost advantage

Question 2.
(a) T_N = (P_x / P_m) x 100 – Net Barter Term of Trade
(b) T = (Q_m / Q_x) x 100 – Income Terms of Trade
(c) T_y = (P_x / P_m) Q_x – Gross Barter Terms of Trade
(d) T_ff = (P_x / P_m)(F_x / F_m) – Single Factoral Terms of Trade
Answer:
(a) T_N = (P_x / P_m) x 100 – Net Barter Term of Trade

Question 3.
(a) SDR – Special Drawing Rights
(b) IMF – India Monetary Fund
(c) BOP – Balance of Price
(d) BOT – Balance of Technology
Answer:
(a) SDR – Special Drawing Rights

Question 4.
(a) NER – Normal Exchange Rate
(b) RER – Real Exchange Ratio
(c) NEER – Normal Effective Exchange Rate
(d) REER – Real Effective Exchange Rate
Answer:
(d) REER – Real Effective Exchange Rate

Question 5.
(a) FDI – Foreign Direct Investment
(b) FOREX – Foreign Export
(c) UDC – Under Development Consumption
(d) MNC – Multi National Country
Answer:
(a) FDI – Foreign Direct Investment

V. Which of the following is not correctly matched.

Question 1.
(a) P₂ – Price level in India
(b) P_f – Price level in abroad (say VS)
(c) e – Nominal exchange rate is flexible
(d) P_x – Price index of exports
Answer:
(c) e – Nominal exchange rate is flexible

Question 2.
(a) Internal Trade – Trade with in Nation
(b) External Trade – Trade between two countries
(c) Balance of Trade – Visible Trade
(d) Income Terms of Trade – Adam smith
Answer:
(d) Income Terms of Trade – Adam smith

Question 3.
(a) FOREX – Foreign Exchange
(b) WTO – World Trade Organisation
(c) FDI – Foreign Direct Investment
(d) IBRD – india Bank Recruitment Development
Answer:
(d) IBRD – india Bank Recruitment Development

Question 4.
(a) Cartels – Economic Integration
(b) Scarce factor – Imports
(c) Factor endowment theory – Ohlin and Ricardo
(d) Labour cost – Unrealistic
Answer:
(c) Factor endowment theory – Ohlin and Ricardo

Question 5.
(a) Intra – regional trade – Internal trade
(b) World Bank – IMF
(c) Types of Exchange Rate – Fixed exchange rate system
(d) Equillibrium Exchange Rate – David Ricardo
Answer:
(d) Equillibrium Exchange Rate – David Ricardo

VI. Pick the odd one out.

Question 1.
The major sectors benefied from FDi in India are ………………….
(a) Financial Sector
(b) Insurance
(c) Telecommunication
(d) Agriculture
Answer:
(d) Agriculture

Question 2.
Determinants of Exchange Rates
(a) Differentials in Inflation
(b) Differntials in Interest Rates
(c) Current Account Deficits
(d) Public people
Answer:
(d) Public people

Question 3.
Types of Exchange Rates
(a) REAL
(b) NEER
(c) Nominal exchange rate
(d) Real exchange rate
Answer:
(a) REAL

Question 4.
Export promotion is ………………….
(a) Reduction of duties
(b) Import Incentives
(c) Export subsidies
(d) Export Incentives
Answer:
(b) Import Incentives

Question 5.
Monetary measures is ………………………
(a) Monetary contraction
(b) Devaluation
(c) Tourism Development
(d) Exchange control
Answer:
(c) Tourism Development

VII. Assertion and Reason.

Question 1.
Assertion (A): David Ricardo was formulated as an explicit and precise theory.
Reason (R): David Ricardo developed the theory of absolute cost advantage.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 2.
Assertion (A): Gains from International trade.
Reason (R): International trade also known as domestic trade.
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 3.
Assertion (A): FDI is an Domestic Economy.
Reason (R): FDI is an Global Economy.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Question 4.
Assertion (A): Exchange control means the state intervention.
Reason (R): Exchange control means the forex market.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 5.
Assertion (A): Price of a commodity is measured by the amount of labour required to produce it.
Reason (R): Trade is one of the Demerit.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Part – B
Answer The Following Questions In One or Two Sentences.

Question 1.
Define “Domestic Trade”?
Answer:

1. It refers to the exchange of goods and services within the political and geographical boundaries of a nation.
2. It is a trade within a country.
3. This is also known as ‘domestic trade’ or ‘home trade’ or ‘intra-regional trade’.

Question 2.
State Ricardo’s Theory of comparative cost advantage criticisms?
Answer:
Criticisms:

1. Labour cost is a small portion of the total cost. Hence, theory based on labour cost is unrealistic.
2. Labourers in different countries are not equal in efficiency.

Question 3.
Write Factor endowment model?
Answer:
Factor endowment model:

1. Developed by Heckscher and Ohlin
2. Countries with a relative factor abundance can specialise and trade
3. Abundance of skilled labour → specialisation → export → exchange for goods are services produced by countries with abundance of unskilled labour
4. Exports embody the abundant factor
5. Imports embody the scarce factor

Question 4.
Write Modern Theory of International Trade differences in comparative costs?
Answer:
Modem Theory of International Trade theory attributes international differences in comparative costs to:

1. Difference in the endowments of factors of production between countries, and
2. Differences in the factor proportions required in production.

Question 5.
Write Modern Theory of International Trade Limitations?
Answer:
Limitations:

1. Factor endowment of a country may change over time.
2. The efficiency of the same factor (say labour) may differ in the two countries. For example, America may be labour scarce in terms of number of workers. But in terms of efficiency, the total labour may be larger.

Question 6.
Define “Visible Trade”?
Answer:
Visible Trade:
Only export and import of commodities are included in the statement of Balance of Trade of a country. Movements of goods (export and imports of commodities) are also known as ‘visible trade’,

Question 7.
Define “Balance of Payments Disequillibrium”?
Answer:
Balance of Payments Disequilibrium:
The BoP is said to be balanced when the receipts (R) and payments (P) are just equal, i.e.,
R / P = 1

Question 8.
Write favourable and unfavourable balance of payments and equations?
Answer:
Favourable BoP:
When receipts exceed payments, the BoP is said to be favourable. That is,
R / P > 1.

Unfavourable BOP:
When receipts are less than payments, the BoP is said to be unfavourable or adverse. That is,
R / P < 1.

Part – C
Answer The Following Questions In One Paragraph.

Question 1.
Write Adam Smith’s theory of Absolute Cost Advantage Assumptions?
Answer:
Assumptions:

1. There are two countries and two commodities (2 x 2 model).
2. Labour is the only factor of production.
3. Labour units are homogeneous.
4. The cost or price of a commodity is measured by the amount of labour required to produce it.
5. There is no transport cost.

Question 2.
Write Ricardo’s Theory of Comparative Cost Advantage Assumptions/
Answer:
Assumptions:

1. There are only two nations and two commodities (2 × 2 model)
2. Labour is the only element of cost of production.
3. All labourer s are of equal efficiency.
4. Labour is perfectly mobile within the country but perfectly immobile between countries.
5. Production is subject to the law of constant returns.
6. Foreign trade is free from all barriers.
7. No change in technology.
8. No transport cost.
9. Perfect competition.
10. Full employment.
11. No government intervention.

Question 3.
What are International Specialization gains?
Answer:
International specialization offers the following gains.

1. Better utilization of resources.
2. Concentration in the production of goods in which it has a comparative advantage.
3. Saving in time.
4. Perfection of skills in production.
5. Improvement in the techniques of production.
6. Increased production.
7. Higher standard of living in the trading countries.

Question 4.
Write favourable and unfavourable balance of Trade?
Answer:
Favourable BOT:
When the total value of commodity exports of a country exceeds the total value of commodity imports of that country, it is said that the country has a ‘favourable’ balance of trade.

Unfavourable BOT:
If total value of commodity exports of a country is less than the total . value of commodity imports of that country, that country is said to have an ‘unfavourable’ balance of trade.

Part – D
Answer The Following Questions In About A page.

Question 1.
Explain the Adam Smith’s Theory of Absolute Cost Advantage Theory and Assumptions with diagram?
Answer:
Adam Smith’s Theory of Absolute Cost Advantage:
Adam Smith argued that all nations can be benefitted when there is free trade and specialisation in terms of their absolute cost advantage.

The Theory:

1. According to Adam Smith, the basis of international trade was absolute cost advantage.

2. Trade between two countries would be mutually beneficial when one country produces a commodity at an absolute cost advantage over the other country which in turn produces another commodity at an absolute cost advantage over the first country.

Assumptions:

1. There are two countries and two commodities (2 × 2 model).
2. Labour is the only factor of production.
3. Labour units are homogeneous.
4. The cost or price of a commodity is measured by the amount of labour required to produce it.
5. There is no transport cost.

Illustration:

Absolute cost advantage theory can be illustrated with the help of the following example.

1. From the illustration, it is clear that India has an absolute advantage in the production of wheat over China and China has an absolute advantage in the production of cloth over India.
2. Therefore, India should specialize in the production of wheat and import cloth from China.
3. China should specialize in the production of cloth and import wheat from India.
4. This kind of trade would be mutually beneficial to both India and China.

Question 2.
Briefly explain the gains from International Trade Categories?
Answer:
Gains from International Trade:

1. International trade helps a country to export its surplus goods to other countries and secure a better market for it.
2. Similarly, international trade helps a country to import the goods which cannot be produced at all or can be produced at a higher cost.
3. The gains from international trade may be categorized under four heads.

I. Efficient Production:

1. International trade enables each participatory country to specialize in the production of goods in which it has absolute or comparative advantages.
2. International specialization offers the following gains.
   1. Better utilization of resources.
   2. Concentration in the production of goods in which it has a comparative advantage.
   3. Saving in time.
   4. Perfection of skills in production.
   5. Improvement in the techniques of production.
   6. Increased production.
   7. Higher standard of living in the trading countries.

II. Equalization of Prices between Countries:
International trade may help to equalize prices in all the trading countries.

1. Prices of goods are equalized between the countries (However, in reality it has not happened).
2. The difference is only with regard to the cost of transportation.
3. Prices of factors of production are also equalized (However, in reality it has not happened).

III. Equitable Distribution of Scarce Materials:
International trade may help the trading countries to have equitable distribution of scarce resources.

IV. General Advantages of International Trade:

1. Availability of variety of goods for consumption.
2. Generation of more employment opportunities.
3. Industrialization of backward nations.
4. Improvement in relationship among countries (However, in reality it has not happened).
5. Division of labour and specialisation.
6. Expansion in transport facilities.

Question 3.
Describe the Types of Terms of Trades?
Answer:
Types of Terms of Trade:
The different concepts of terms of trade were classified by Gerald M.Meier into the following three categories:
Terms of Trade related to the Ratio of Exchange between Commodities:

1. Net Barter Terms of Trade:

1. This type was developed by Taussig in 1927.
2. The ratio between the prices of exports and of imports is called the “net barter terms of trade’.
3. It is named by Viner as the ‘commodity terms of trade’.

It is expressed as:
T_n = (P_x / P_m ) × 100
Where,
T_n = Net Barter Terms of Trade
P_x = Index number of export prices
P_m = Index number of import prices
This is used to measure the gain from international trade.
If ‘T_n’ is greater than 100, then it is a favourable terms of trade which will mean that for a rupee of export, more of imports can be received by a country.

2. Gross Barter Terms of Trade:

1. This was developed by Taussig in 1927 as an improvement over the net terms of trade.
2. It is an index of relationship between total physical quantity of imports and the total physical quantity of exports.

T = (Q_m / Q_x) × 100 Where,
Q_m = Index of import quantities .
Q_x = Index of export quantities
If for a given quantity of export, more quantity of import can be consumed by a country, then one can say that terms of trade are favourable.

3. Income Terms of Trade:

1. The income terms of trade was given by G.S.Dorrance in 1948.
2. It is the index of the value of exports divided by the price index for imports multiplied by quantity index of experts.
3. In other words, it is the net barter terms of trade of a country multiplied by its exports – volume index.

T = (P_x / P_m) Q
Where,
P_x = Price index of exports
P_m = Price index of imports
Q_x = Quantity index of exports

Question 4.
Briefly explain causes for Balance of payments disequillibrium?
Answer:
Causes for BoP Disequilibrium:
The following are the major causes producing disequilibrium in the balance of payments of a country.

(I) Cyclical Fluctuation:

1. Cyclical disequilibrium in different countries is caused by their cyclical fluctuations, their phases and magnitude.
2. World trade shrinks during depression while trade flourishes during prosperity.

(II) Structural Changes:

1. Structural disequilibrium is caused by the structural changes brought by huge development and investment programmes in the developing economies.
2. Such economies may have high propensity to import for want of capital for rapid industrialization, while export may not be boosted up to that extent.

(III) Development Expenditure:

1. Development disequilibrium is caused by rapid economic development which results in income and price effects.
2. The less developed countries in the early stage of development are not self sufficient.
3. Income, savings and investment are abysmally low.
4. They depend upon developed countries for import of commodities, capital and technology.
5. Export potential is low and import intensity is high.
6. So the LDCs suffer from adverse BoP.

(IV) Consumerism:

1. Balance of payments position of a country is adversely affected by a huge increase in consumption.
2. This increases the need for imports and decreases the capacity to export.

(V) Demonstration Effect:

1. Deficit in the balance of payments of developing countries is also caused by demonstration effect which influences the people in UDCs to imitate western styled goods.
2. This will raise the propensity to import causing adverse balance of payments.
3. This is good for the developed countries.

(VI) Borrowing:

1. International borrowing and investment may cause a deficit in the balance of payments.
2. When the international borrowing is heavy, a country’s balance of payments will be adverse since it repays loans with interest.
3. Servicing of debt is a huge burden. That is why the UDCs are forced to borrow more, (viz) Technological Backwardness:
4. Due to technological backwardness, the people (Indians) are unable to use the energy (Solar) available with them.
5. As a result they import huge petroleum products from foreign countries, increasing the trade deficit.

(VII) Technological Backwardness:

1. Due to technological backwardness, the people (Indians) are unable to use the energy (Solar) available with them.
2. As a result they import huge petroleum products from foreign countries, increasing the trade deficit.

(VIII) Global Politics:

1. The rich countries (e.g. USA) need to sell their weapons to promote their economy and generate employment.

2. Hence, wars between countries (for example Iran and Irag, Pakistan and India) are stimulated In order to win the wars, the poor countries are forced to buy the weapons from weapon – rich countries, using their export earnings and creating trade deficit.

3. Thus UDCs are trapped forever.

Students can Download Economics Chapter 5 Monetary Economics Questions and Answers, Notes Pdf, Samacheer Kalvi 12th Economics Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 5 Monetary Economics

Samacheer Kalvi 12th Economics Monetary Economics Text Book Back Questions and Answers

Part – A
Multiple Choice Questions.

Question 1.
The RBI Headquarters is located at ………………………
(a) Delhi
(b) Chennai
(c) Mumbai
(d) Bengalore
Answer:
(c) Mumbai

Question 2.
Money is ………………………
(a) Acceptable only when it has intrinsic value
(b) Constant in purchasing power
(c) The most liquid of all assets
(d) Needed for allocation of resources
Answer:
(c) The most liquid of all assets

Question 3.
Paper currency system is managed by the ………………………
(a) Central Monetary authority
(b) State Government
(c) Central Government
(d) Banks
Answer:
(a) Central Monetary authority

Question 4.
The basic distinction between M₁ and M₂ is with regard to ………………………
(a) Post office deposits
(b) Time deposits of banks
(c) Saving deposits of banks
(d) Currency
Answer:
(b) Time deposits of banks

Question 5.
Irving Fisher’s Quantity Theory of Money was popularized in ………………………
(a) 1908
(b) 1910
(c) 1911
(d) 1914
Answer:
(c) 1911

Question 6.
MV stands for ………………………
(a) Demand for money
(b) Supply of legal tender money
(c) Supply of bank money
(d) Total supply of money
Answer:
(b) Supply of legal tender money

Question 7.
Inflation means ………………………
(a) Prices are rising
(b) Prices are falling
(c) Value of money is increasing
(d) Prices are remaining the same
Answer:
(a) Prices are rising

Question 8.
………………………. inflation results in a serious depreciation of the value of money.
(a) Creeping
(b) Walking
(c) Running
(d) Hyper
Answer:
(d) Hyper

Question 9.
…………………… inflation occurs when general prices of commodities increases due to increase in production costs such as wages and raw materials.
(a) Cost – push
(b) Demand pull
(c) Running
(d) Galloping
Answer:
(a) Cost – push

Question 10.
During inflation, who are the gainers?
(a) Debtors
(b) Creditors
(c) Wage and salary earners
(d) Government
Answer:
(a) Debtors

Question 11.
…………………… is a decrease in the rate of inflation.
(a) Disinflation
(b) Deflation
(c) Stagflation
(d) Depression
Answer:
(a) Disinflation

Question 12.
Stagflation combines the rate of inflation with ……………………
(a) Stagnation
(b) Employment
(c) Output
(d) Price
Answer:
(a) Stagnation

Question 13.
The study of alternating fluctuations in business activity is referred to in Economics as ……………………
(a) Boom
(b) Recession
(c) Recovery
(d) Trade cycle
Answer:
(d) Trade cycle

Question 14.
During depression the level of economic activity becomes extremely ……………………
(a) High
(b) Bad
(c) Low
(d) Good
Answer:
(c) Low

Question 15.
“Money can be anything that is generally acceptable as a means of exchange and that the same time acts as a measure and a store of value”, This definition was given by ……………………
(a) Crowther
(b) A.C.Pigou
(c) F.A.Walker
(d) Francis Bacon
Answer:
(a) Crowther

Question 16.
Debit card is an example of ……………………
(a) Currency
(b) Paper currency
(c) Plastic money
(d) Money
Answer:
(c) Plastic money

Question 17.
Fisher’s Quantity Theory of money is based on the essential function of money as ……………………
(a) Measure of value
(b) Store of value
(c) Medium of exchange
(d) Standard of deferred payment
Answer:
(c) Medium of exchange

Question 18.
V in MV = PT equation stands for ……………………
(a) Volume of trade
(b) Velocity of circulation of money
(c) Volume of transaction
(d) Volume of bank and credit money
Answer:
(b) Velocity of circulation of money

Question 19.
When prices rise slowly, we call it ……………………
(a) Galloping inflation
(b) Mild inflation
(c) Hyper inflation
(d) Deflation
Answer:
(b) Mild inflation

Question 20.
…………………… inflation is in no way dangerous to the economy.
(a) Walking
(b) Running
(c) Creeping
(d) Galloping
Answer:
(c) Creeping

Part – B
Answer The Following Questions In One or Two Sentences.

Question 21.
Define Money?
Answer:

1. Many economists developed definition for money. Among these, definitions of Walker and Crowther are given below:
   “Money is, what money does ” – Walker.
2. “Money can be anything that is generally acceptable as a means of exchange and at the same time acts as a measure and a store of value”. – Crowther
3. Money is anything that is generally accepted as payment for goods and services and repayment of debts and that serves as a medium of exchange.
4. A medium of exchange is anything that is widely accepted as a means of payments.

Question 22.
What is barter?
Answer:

1. Before money was invented, exchange took place by Barter, that is, commodities and services were directly exchanged for other commodities and services.
2. Such exchange of goods for goods was known as “Barter Exchange” or “Barter System”.

Question 23.
What is commodity money?
Answer:

1. After the barter system and commodity money system, modem money systems evolved.
2. Among these, metallic standard is the premier one. ,
3. Under metallic standard, some kind of metal either gold or silver is used to determine the standard value of the money and currency.
4. Standard coins made out of the metal are the principal coins used under the metallic standard.
5. These standard coins are full bodied or full weighted legal tender.
6. Their face value is equal to their intrinsic metal value.

Question 24.
What is gold standard?
Answer:

1. Gold Standard is a system in which the value of the monetary unit or the standard currency is directly linked with gold.
2. The monetary unit is defined in terms of a certain weight of gold.
3. The purchasing power of a unit of money is maintained equal to the value of a fixed weight of gold.

Question 25.
What is plastic money? Give example?
Answer:

1. The latest type of money is plastic money.
2. Plastic money is one of the most evolved forms of financial products.
3. Plastic money is an alternative to the cash or the standard “money”.
4. Plastic money is a term that is used predominantly in reference to the hard plastic cards used every day in place of actual bank notes.
5. Plastic money can come in many different forms such as Cash cards, Credit cards, Debit cards, Pre-paid Cash cards, Store cards, Forex cards and Smart cards.
6. They aim at removing the need for carrying cash to make transactions.

Question 26.
Define inflation?
Answer:

1. Inflation is a consistent and appreciable rise in the general price level.
2. In other words, inflation is the rate at which the general level of prices for goods and services is rising and consequently the purchasing power of currency is falling.
3. “Too much of Money chasing too few goods” – Coulbourn
4. “A state of abnormal increase in the quantity of purchasing power” – Gregorye

Question 27.
What is Stagflation?
Answer:
Stagflation is a combination of stagnant economic growth, high unemployment and high inflation.

Part – C
Answer The Following Questions In One Paragraph.

Question 28.
Write a note on metallic money?
Answer:

1. After the barter system and commodity money system, modem money systems evolved.
2. Among these, metallic standard is the premier one.
3. Under metallic standard, some kind of metal either gold or silver is used to determine the standard value of the money and currency.
4. Standard coins made out of the metal are the principal coins used under the metallic standard. Monetary Economics 93
5. These standard coins are full bodied or Ml weighted legal tender.
6. Their face value is equal to their intrinsic metal value.

Question 29.
What is money supply?
Answer:

1. Money supply means the total amount of money in an economy.
2. It refers to the amount of money which is in circulation in an economy at any given time.
3. Money supply plays a crucial role in the determination of price level and interest rates.
4. Money supply viewed at a given point of time is a stock and over a period of time it is a flow.

Question 30.
What are the determinants of money supply?
Answer:
Determinants of Money Supply:

1. Currency Deposit Ratio (CDR); It is the ratio of money held by the public in currency to that they hold in bank deposits.
2. Reserve deposit Ratio (RDR); Reserve Money consists of two things (a) vault cash in banks and (b) deposits of commercial banks with RBI.
3. Cash Reserve Ratio (CRR); It is the fraction of the deposits the banks must keep with RBI. (z’v) Statutory Liquidity Ratio (SLR); It is the fraction of the total demand and time deposits of the commercial banks is the form of specified liquid assests.

Question 31.
Write the types of inflation?
Answer:
The four types of inflation are –
1. Creeping Inflation:
Creeping inflation is slow-moving and very mild. The rise in prices will not be perceptible but spread over a long period. This type of inflation is in no way dangerous to the economy. This is also known as mild inflation or moderate inflation.

2. Walking Inflation:
When prices rise moderately and the annual inflation rate is a single digit . (3% – 9%), it is called walking or trolling inflation.

3. Running Inflation:
When prices rise rapidly like the running of a horse at a rate of speed of 10% – 20% per annum, it is called running inflation.

4. Galloping inflation:
Galloping inflation or hyper inflation points out to unmanageably high inflation rates that run into two or three digits. By high inflation the percentage of the same is almost 20%
to 100% from an overall perspective.

Other types of inflation (on the basis of inducement):

1. Currency inflation:
The excess supply of money in circulation causes rise in price level.

2. Credit inflation:
When banks are liberal in lending credit, the money supply increases and thereby rising prices. .

3. Deficit induced inflation:
The deficit budget is generally financed through printing of currency by the Central Bank. As a result, prices rise.

4. Profit induced inflation:
When the firms aim at higher profit, they fix the price with higher margin. So prices go up.

5. Scarcity induced inflation:
Scarcity of goods happens either due to fall in production (e.g. farm goods) or due to hoarding and black marketing. This also pushes up the price. (This has happened is Venezula in the year 2018).

6. Tax induced inflation:
Increase in indirect taxes like excise duty, custom duty and sales tax may lead to rise in price (e.g. petrol and diesel). This is also called taxflation.

Question 32.
Explain Demand-pull and Cost push inflation?
Answer:
Demand – Pull Vs Cost – Push inflation:

1. Demand – Pull Inflation:
Demand and supply play a crucial role in deciding the inflation levels in the society at all points of time. For instance, if the demand is high for a product and supply is low, the price of the products increases.

2. Cost – Push Inflation:
When the cost of raw materials and other inputsrises inflation results. Increase in wages paid to labour also leads to inflation.

Question 33.
State Cambridge equations of value of money?
Answer:
Cambridge Approach (Cash Balances Approach):

1. Marshall’s Equation:
The Marshall equation is expressed as:
M = KPY
Where
M is the quantity of money Y is the aggregate real income of the community . P is Purchasing Power of money
K represents the fraction of the real income which the public desires to hold in the form of money.
Thus, the price level P = M/KY or the value of money (The reciprocal of price level) is 1/P = KY/M
The value of money in terms of this equation can be found out by dividing the total quantity of goods which the public desires to holdout of the total income by the total supply of money. According to Marshall’s equation, the value of money is influenced not only by changes in M, but also by changes in K.

2. Keynes’Equation
Keynes equation is expressed as:
n = pk (or) p = n / k
Where
n is the total supply of money p is the general price level of consumption goods
k is the total quantity of consumption units the people decide to keep in the form of cash, Keynes indicates that K is a real balance, because it is measured in terms of consumer goods. According to Keynes, peoples’ desire to hold money is unaltered by monetary authority. So, price level and value of money can be stabilized through regulating quantity of money (n) by the monetary authority.
Later, Keynes extended his equation in the following form:
n = p (k + rk’) or p = n / (k + rk’)
Where,
n = total money supply p = price level of consumer goods
k = peoples’ desire to hold money in hand (in terms of consumer goods) in the total income of them
r = cash reserve ratio
k’ = community’s total money deposit in banks, in terms of consumers goods.
In this extended equation also, Keynes assumes that, k, k’ and r are constant. In this situation, price level (P) is changed directly and proportionately changing in money volume (n).

Question 34.
Explain disinflation?
Answer:
Disinflation:
Disinflation is the slowing down the rate of inflation by controlling the amount of credit (bank loan, hire purchase) available to consumers without causing more unemployment. Disinflation may be defined as the process of reversing inflation without creating unemployment or reducing output in the economy.

Part – D
Answer the following questions in one page.

Question 35.
Illustrate Fisher’s Quantity theory of money?
Answer:
(a) Fisher’s Quantity Theory of Money:
The quantity theory of money is a very old the¬ory. It was first propounded in 1588 by an Italian economist, Davanzatti. But, the credit for popularizing this theory in recent years rightly belongs to the well-known American economist, Irving Fisher who published his book, ‘The Purchasing Power of Money” in 1911. He gave it a quantitative form in terms of his famous “Equation of Exchange”.
The general form of equation given by Fisher is –
MV = PT

1. Fisher points out that in a country during any given period of time, the total quantity of money (MV) will be equal to the total value of all goods and services bought and sold (PT). MV = PT
Supply of Money = Demand for Money

2. This equation is referred to as “Cash Transaction Equation”.
Where M = Money Supply/quantity of Money
V = Velocity of Money
P = Price level
T = Volume of Transaction.
It is expressed as P = MV / T which implies that the quantity of money determines the price level and the price level in its turn varies directly with the quantity of money, provided ‘V’ and ‘T’ remain constant.

3. According to Marshall, peoples desire to hold money (the coefficient, K) is more powerful in determination of money, rather than quantity of money (M). So, peoples’ desire to hold money is a determinant of value of money.

4. The above equation considers only currency money. But, in a modem economy, bank’s demand deposits or credit money and its velocity play a vital part in business. Therefore, Fisher extended his original equation of exchange to include bank deposits M, and its velocity Vr The revised equation was:
PT = MV + M₁V₁
P = \(\frac { MV+M_{ 1 }V_{ 1 } }{ T } \)

5. From the revised equation, it is evident, that the price level is determined by (a) the quantity of money in circulation ‘M’ (b) the velocity of circulation of money ‘V’ (c) the volume of bank credit money M₁ (d) the velocity of circulation of credit money V₁, and the volume of trade (T)

Diagramatic Illustration:

Quantity of Money

1. Figure (A) shows the effect of changes in the quantity of money on the price level. When the quantity of money is OM, the price level is OP. When the quantity of money is doubled to OM₂, the price level is also doubled to OP₂. Further, when the quantity of money is increased four – fold to OM₄, the price level also increases by four times to OP₄. This relationship is expressed by the curve OP = f (M) from the origin at 45°.

2. Figure (B), shows the inverse relation between the quantity of money and the value of money, where the value of money is taken on the vertical axis. When the quantity of money is OM₁, the value of money is 01 / P₁. But with the doubling of the quantity of money to OM₂, the value of money becomes one – half of what it was before, (01 / P₂). But, with the quantity of money increasing by four – fold to OM₄, the value of money is reduced by 01 / P₄. This inverse relationship between the quantity of money and the value of money is shown by downward sloping curve 1 / OP = f (M).

Question 36.
Explain the functions of money?
Answer:

1. Primary Functions:

(I) Money as a medium of exchange:
This is considered as the basic function of money. Money has the quality of general acceptability, and all exchanges take place in terms of money.

(II) Money as a measure of value:
The second important function of money is that it measures the value of goods and services. In other words, the prices of all goods and services are expressed in terms of money. Money is thus looked upon as a collective measure of value.

2. Secondary Functions:

(I) Money as a Store of value:
Savings done in terms of commodities were not permanent. But, with the invention of money, this difficulty has now disappeared and savings are now done in terms of money. Money also serves as an excellent store of wealth, as it can be easily converted into other marketable assets, such as, land, machinery, plant etc.

(II) Money as a Standard of Deferred Payments:
Borrowing and lending were difficult problems under the barter system. In the absence of money, the borrowed amount could be returned only in terms of goods and services. But the modem money – economy has greatly facilitated the borrowing and lending processes.

(III) Money as a Means of Transferring Purchasing Power:
The field of exchange also went on extending with growing economic development. The exchange of goods is now extended to distant lands.

3. Contingent Functions:

(I) Basis of the Credit System:
Money is the basis of the Credit System. Business transactions are either in cash or on credit.

(II) Money facilitates distribution of National Income:
The task of distribution of national income was exceedingly complex under the barter system.

(III) Money helps to Equalize Marginal Utilities and Marginal Productivities:
Consumer can obtain maximum utility only if he incurs expenditure on various commodities in such a manner as to equalize marginal utilities accruing from them. Now in equalizing these marginal utilities, money plays an important role, because the prices of all commodities are expressed in money.

(IV) Money Increases Productivity of Capital:
Money is the most liquid form of capital. In other words, capital in the form of money can be put to any use.

4. Other Functions:

(I) Money helps to maintain Repayment Capacity:
Money possesses the quality of general acceptability. To maintain its repayment capacity, every firm has to keep assets in the form of liquid cash. The firm ensures its repayment capacity with money.

(II) Money represents Generalized Purchasing Power:
Purchasing power kept in terms of money can be put to any use. It is not necessary that money should be used only for the purpose for which it has been served.

(III) Money gives liquidity to Capital:
Money is the most liquid form of capital. It can be put to any use.

Question 37.
What are the causes and effects of inflation on the economy?
Answer:
Causes of Inflation:
The main causes of inflation in India are as follows:

1. Increase in Money Supply:
Inflation is caused by an increase in the supply of money which leads to increase in aggregate demand. The higher the growth rate of the nominal money supply, the higher is the rate of inflation.

2. Increase in Disposable Income:
When the disposable income of the people increases, it raises their demand for goods and services. Disposable income may increase with the rise in national income or reduction in taxes or reduction in the saving of the people.

3. Increase in Pubiic Expenditure:
Government activities have been expanding due to developmental activities and social welfare programmes. This is also a cause for price rise.

4. Increase in Consumer Spending:
The demand for goods and services increases when they are given credit to buy goods on hire-purchase and installment basis.

5. Cheap Monetary Policy:
Cheap monetary policy or the policy of credit expansion also leads to increase in the money supply which raises the demand for goods and services in the economy.

6. Deficit Financing:
In order to meet its mounting expenses, the government resorts to deficit financing by borrowing from the public and even by printing more notes.

7. Black Assests, Activities and Money:
The existence of black money and black assests due to corruption, tax evasion etc., increase the aggregate demand. People spend such money, lavishly. Black marketing and hoarding reduces the supply of goods.

8. Repayment of Public Debt:
Whenever the government repays its past internal debt to the public, it leads to increase in the money supply with the public.

9. Increase in Exports:
When exports are encouraged, domestic supply of goods decline. So prices rise.

Effects of Inflation:
The effects of inflation can be classified into two heads:

1. Effects on Production and
2. Effects on Distribution.

1. Effects on Production:
When the inflation is very moderate, it acts as an incentive to traders and producers. This is particularly prior to full employment when resources are not fully utilized. The profit due to rising prices encourages and induces business class to increase their investments in production, leading to generation of employment and income.

(I) However, hyper – inflation results in a serious depreciation of the value of money.

(II) When the value of money undergoes considerable depreciation, this may even drain out the foreign capital already invested in the country.

(III) With reduced capital accumulation, the investment will suffer a serious set-back which may have an adverse effect on the volume of production in the country.

(IV) Inflation also leads to hoarding of essential goods both by the traders as well as the consumers and thus leading to still hiher inflation rate.

(V) Inflation encourages investment in speculative activities rather than productive purposes.

2. Effects on Distribution:

1. Debtors and Creditors:
During inflation, debtors are the gainers while the creditors are losers.

2. Fixed – income Groups:
The fixed income groups are the worst hit during inflation because their incomes being fixed do not bear any relationship with the rising cost of living.

3. Entrepreneurs:
Inflation is the boon to the entrepreneurs whether they are manufacturers, traders, merchants or businessmen, because it serves as a tonic for business enterprise.

4. Investors:
The investors, who generally invest in fixed interest yielding bonds and securities have much to lose during inflation.

Question 38.
Describe the phases of Trade cycle?
Answer:
Phases of Trade Cycle
The four different phases of trade cycle is referred to as

1. Boom
2. Recession
3. Depression and
4. Recovery. These are illustrated in the figure:

Phases of Trade Cycle:

1. Boom or Prosperity Phase:
The full employment and the movement of the economy beyond full employment is characterized as boom period.

1. During this period, there is hectic activity in economy.
2. Money wages rise, profits increase and interest rates go up.
3. The demand for bank credit increases and there is all – round optimism.

2. Recession:

1. The turning point from boom condition is called recession.
2. This happens at higher rate, than what was earlier.
3. Generally, the failure of a company or bank bursts the boom and brings a phase of recession.
4. Investments are drastically reduced, production comes down and income and profits decline.
5. There is panic in the stock market and business activities show signs of dullness.
6. Liquidity preference of the people rises and money market becomes tight.

3. Depression:

1. During depression the level of economic activity becomes extremely low.
2. Firms incur losses and closure of business becomes a common feature and the ultimate result is unemployment.
3. Interest prices, profits and wages are low. The agricultural class and wage earners would be worst hit.
4. Banking institutions will be reluctant to advance loans to businessmen.
5. Depression is the worst phase of the business cycle.
6. Extreme point of depression is called as “trough”, because it is a deep point in business cycle.

4. Recovery:

1. After a period of depression, recovery sets in.
2. This is the turning point from depression to revival towards upswing.
3. It begins with the revival of demand for capital goods.
4. Autonomous investments boost the activity.
5. The demand slowly picks up and in due course the activity is directed towards the upswing with more production, profit, income, wages and employment.
6. Recovery may be initiated by innovation or investment or by government expenditure (autonomous investment).

Samacheer Kalvi 12th Economics Consumption and Investment Functions Additional Questions

Part – A
I. Multiple Choice Questions.

Question 1.
During Inflation?
(a) Business men gain
(b) Wage earners gain
(c) Salary gain
(d) Renters gain
Answer:
(a) Business men gain

Question 2.
Galloping Inflation is also known as –
(a) Deflation
(b) Persistent Inflation
(c) Stagflation
(d) Cost – push Inflation
Answer:
(b) Persistent Inflation

Question 3.
The modem economy is described as –
(a) Demand Economy
(b) Supply Economy
(c) Money Economy
(d) Wage Economy
Answer:
(c) Money Economy

Question 4.
The term ………………………… refers to a phase or policy when interest rates are high.
(a) Purchasing money
(b) Power money
(c) Fiat money
(d) Dear money
Answer:
(d) Dear money

Question 5.
Currency notes in circulation are referred to as –
(b) Fiat money
(c) Value of money
(d) Cheap money
Answer:
(b) Fiat money

Question 6.
What is the name of inflation without a rise in price level?
(a) Repressed Inflation
(b) Hyper Inflation
(c) Galloping Inflation
(d) Cost – Push Inflation
Answer:
(a) Repressed Inflation

Question 7.
Give the example of a country that experienced hyper Inflation?
(a) India
(b) China
(c) Germany
(d) Africa
Answer:
(c) Germany

Question 8.
Which is the most important function of money?
(a) Measure of value
(b) Store of value
(c) Medium of exchange
(d) Standard of deferred payments
Answer:
(c) Medium of exchange

Question 9.
What is the other name for “Equation of Exchange”?
(a) Fisher’s Equation
(b) Keynes Equation
(c) Marshall’s Equation
(d) Equation of Exchange
Answer:
(a) Fisher’s Equation

Question 10.
What is the cheap money policy?
(a) High rates of Interest
(b) Low rates of Interest
(c) Medium rates of Interest
(d) Very high rates of Interest
Answer:
(b) Low rates of Interest

Question 11.
Monetary policy is controlled by –
(a) Central bank
(b) State Government
(c) Private sector
(d) Central Government
Answer:
(d) Central Government

Question 12.
………………………… is usually effective for controlling inflation.
(a) Monetary policy
(b) RBI
(c) State Government
(d) Central government
Answer:
(a) Monetary policy

Question 13.
Monetary policy is usually effective in controlling –
(a) Bank
(b) Inflation
(c) Deflation
(d) Stagflation
Answer:
(b) Inflation

Question 14.
Money acts as a common measure of –
(a) Reserve money
(b) Fiat money
(c) Value
(d) Broad money
Answer:
(c) Value

Question 15.
Bank rate is lowered during –
(a) Inflation
(b) Price
(c) Employment
(d) Deflation
Answer:
(d) Deflation

Question 16.
Under dear money policy is –
(a) Rate of Interest is low
(b) Rate of interest is high
(c) Bank rate is high
(d) Money supply is more
Answer:
(b) Rate of interest is high

Question 17.
M₃ is called –
(a) Narrow money
(b) Reserve money
(c) Broad money
(d) Fiat money
Answer:
(c) Broad money

Question 18.
Price mechanism plays a vital role in –
(a) Capitalism
(b) Socialism
(c) Mixed economy
(d) Traditional economy
Answer:
(a) Capitalism

Question 19.
“Money is what money does” ………………………… this definition was given by –
(a) Crowther
(b) Fisher
(c) Grasham
(d) Walker
Answer:
(d) Walker

Question 20.
Currency with the public is known as –
(a) M₁
(b) M₂
(C) M₃
(d) M₄
Answer:
(a) M₁

Question 21.
Cost – push inflation is induced by rising –
(a) Costs
(b) Money
(c) Broad money
(d) Inflation
Answer:
(b) Money

Question 22.
The direct exchange of goods for goods is known as –
(a) Money exchange
(b) Money transfer
(c) Barter System
(d) Barter goods
Answer:
(c) Barter System

Question 23.
Money is a matter of functions –
(a) One
(b) Two
(c) Three
(d) Four
Answer:
(d) Four

Question 24.
Deflation is a period marked by ………………………… prices.
(a) Increasing
(b) Falling
(c) Constant
(d) High
Answer:
(d) High

Question 25.
Dear money refers to ………………………… rate being high.
(a) Money
(b) Finance
(c) Interest
(d) Cost
Answer:
(c) Interest

II. Match the following and choose the correct answer by using codes given below

A. Deficit financing – (i) Monetary policy objectives
B. Store of value – (ii) Currency notes
C. Price stability – (iii) Causes inflation
D. Fiat money – (iv) Function of money
Codes:
(a) A (iii) B (iv) C (i) D (ii)
(b) A (ii) B (iii) C (iv) D (i)
(c) A (iv) B (ii) C (iii) D (i)
(d) A (i) B (iv) C (ii) D (iii)
Answer:
(a) A (iii) B (iv) C (i) D (ii)

Question 2.
A. Falling prices – (i) Black money
B. Government securities – (ii) Business loss
C. Bank rate – (iii) Open Market operation
D. Unaccounted money – (iv) Credit control
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iii) C (iv) D (i)
(c) A (iii) B (iv) C (i) D (ii)
(d) A (iv) B (i) C (ii) D (iii)
Answer:
(b) A (ii) B (iii) C (iv) D (i)

Question 3.
A. Checking Inflation – (i) Irving Fisher
B. Great Depression – (ii) Narrow money
C. Quantity theory of money – (iii) Wage freeze
D. M₁ – 1930
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (iv) C(i) D (ii)
(c) A (ii) B (iii) C (iv) D (i)
(d) A (iv) B (i) C (ii) D (iii)
Answer:
(b) A (iii) B (iv) C(i) D (ii)

Question 4.
A. Cheap money policy – (i) Purchasing money
B. Prices pushed – (ii) Creeping inflation
C. Value of money – (iii) Low rate of interest
D. Selective credit control – (iv) Moral suasion
Codes:
(a) A (iii) B (ii) C (i) D (iv)
(b) A (ii) B (i) C (iv) D (iii)
(c) A (iv) B (iii) C (ii) D (i)
(d) A (i) B (iv) C (iii) D (ii)
Answer:
(a) A (iii) B (ii) C (i) D (iv)

Question 5.
A. Galloping Inflation – (i) Money Act
B. M₃is called – (ii) Hyperinflation
C. Measure of value – (iii) Broad money
D. Deflation Codes – (iv) Bank rate
Codes:
(a) A (i) B (ii) C (iv) D (iii)
(b) A (iv) B (i) C (iii) D (ii)
(c) A (iii) B (iv) C (ii) D (i)
(d) A (ii) B (iii) C (i) D (iv)
Answer:
(d) A (ii) B (iii) C (i) D (iv)

III. State whether the statements are true or false.

Question 1.
(i) Inflation is taxation without legislation was said by Milton Friedman.
(ii) Money is the most liquid form of capital.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 2.
(i) “The purchasing power of money” was a book published by Irving Fisher in 1911.
(ii) The general form of equation given by Fisher is M = KPY.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 3.
(i) The study of alternating fluctuations in business activity is referred to in Economics as Trade cycle.
(ii) During depression the level of economic activity becomes extremely high.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 4.
(i) Creeping Inflation is in no way dangerous to the economy.
(ii) Debit card is an example of paper currency.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 5.
(i) MV = PT equation stands for volume of Trade.
(ii) Fisher’s Quantity Theory of money is based on the essential function of money as measure of value.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(b) Both (i) and (ii) are false

IV. Which of the following is correctly matched:

Question 1.
(a) Medium of exchange – CRR
(b) Cash Reserve Ratio – Gold standard
(c) Goods exchange for goods – Barter system
(d) Full weighted legal tender – Plastic money
Answer:
(c) Goods exchange for goods – Barter system

Question 2.
(a) Depression – Starting stage
(b) Recession – Turning point from boom
(c) Boom – Economic activities
(d) Inflation – Hectic activity
Answer:
(b) Recession – Turning point from boom

Question 3.
(a) Store of value – Liquidity cash
(b) Deflation – Rise in price
(c) Trade cycle – Narrow money
(d) Quantity theory of money – J.M. Keynes
Answer:
(d) Quantity theory of money – J.M. Keynes

Question 4.
(a) The purchasing power of currency – Falling
(b) Monetary measures are adopted by – State bank
(c) The turning point from boom is – Inflation
(d) Money supply means the total – Inflation amount of money in – World
Answer:
(a) The purchasing power of currency – Falling

Question 5.
(a) The Marshall’s equation – MV = PT
(b) Cash Reserve Ratio – CRR
(c) Statutory Liquidity cash – SLC
(d) Functions of money – Money supply
Answer:
(b) Cash Reserve Ratio – CRR

Question 6.
(a) Barter System – Technology
(b) Gold Standard – Standard currency is directly linked with gold
(c) Plastic money – Money value
(d) Paper money – Smart card
Answer:
(b) Gold Standard – Standard currency is directly linked with gold

V. Which of the following is not correctly matched:

Question 1.
(a) Inflation – Rise in price
(b) Deflation – Fall in price
(c) Hyper Inflation – India
(d) Hyper deflation – Phases of Trade cycle
Answer:
(c) Hyper Inflation – India

Question 2.
(a) Currency Deposit Ratio – CDR
(b) Reserve Deposit Ratio – RDR
(c) Cash Reserve Ratio – CRR
(d) Statutory Liquidity Ratio – SRL
Answer:
(d) Statutory Liquidity Ratio – SRL

Question 3.
(a) M – Money supply / Quantity of money –
(b) V – Velocitu of money
(c) P – Price level
(d) T – Price rise slow moving
Answer:
(d) T – Price rise slow moving

Question 4.
(a) Creeping Inflation – Price rise slow moving
(b) Walking Inflation – Price rise moderately
(c) Running Inflation – Price rise rapidly running
(d) Galloping Inflation – Price rise very slow
Answer:
(d) Galloping Inflation – Price rise very slow

Question 5.
(a) Money supply – Central Bank
(b) Dear money policy – During Inflation
(c) Value of money – Purchasing power
(d) Black money – Narrow money
Answer:
(d) Black money – Narrow money

VI. Pick the odd one out.

Question 1.
The main functions of money can be classified
(a) Primary functions
(b) Secondary functions
(c) Contingent functions
(d) Territory functions
Answer:
(d) Territory functions

Question 2.
Money secondary functions are
(a) Money as a store of value
(b) Money as a standard of Deferred payments
(c) Money as a means of Transferring purchasing power
(d) Money as a modem exchange system
Answer:
(d) Money as a modem exchange system

Question 3.
Contingent functions are called
(a) Basis of the credit system
(b) Money facilitates distribution of state income
(c) Money’helps to equalize marginal utility
(d) Money increases productivity of capital
Answer:
(b) Money facilitates distribution of state income

Question 4.
RBI publishes information of money supply are
(a) M₂ = Currency coins and demand deposits
(b) M₂ = M₁ + Saving deposits with post office savings banks and Total Deposits
(c) M₃ = M₂ + Time deposits of all commercial and co – operative banks
(d) M₄ = M₃ + Total deposits with post offices
Answer:
(b) M₂ = M₁ + Saving deposits with post office savings banks and Total Deposits

Question 5.
Determinants of money supply are
(a) Consumer Deposit Ratio (CDR)
(b) Reserve Deposit Ratio (RDR)
(c) Cash Reserve Ratio (CRR)
(d) Statutory Liquidity Ratio (SLR)
Answer:
(a) Consumer Deposit Ratio (CDR)

Question 6.
Types of Inflation are
(a) Currency Inflation
(b) Credit Inflation
(c) Demand Induced Inflation
(d) Profit Induced Inflation
Answer:
(c) Demand Induced Inflation

Question 7.
The four different phases of trade cycle is referred to as
(a) Regression
(b) Recession
(c) Depression
(d) Recovery
Answer:
(a) Regression

VII. Assertion and Reason.

Question 1.
Assertion (A): Stagflation is a combination of stagnant economic growth, high unemployment and high inflation.
Reason (R): Stagflation is the slowing down the rate of inflation by controlling the amount of credit.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 2.
Assertion (A): Keynes and Milton Friedman together suggested Monetary measures, Fiscal measures and other measures to prevent and control of inflation.
Reason (R): Keynes and Milton Friedman together suggested other measures are Short term and Long – term measures.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 3.
Assertion (A): A trade cycle refers to oscillations in aggregate economic activity particularly in employment, output, income, etc.
Reason (R): The four different phases of trade cycle is referred to Boom, Recession, Depression and Recovery.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 4.
Assertion (A): Fiscal policy is now recognized as an important instrument to tackle an inflationary situation.
Reason (R): Monetary measures are adopted by the central bank.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 5.
Assertion (A): Currency is created by the RBI and Union Government.
Reason (R): Bank deposits are created by commercial banks and co-operative banks.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 6.
Assertion (A): Recovery may be initiated by Money balance.
Reason (R): Recovery may be government expenditure.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Part – B
Answer The Following Questions In One or Two Sentences.

Question 1.
Define “Silver Standard”?
Answer:
Silver Standard: The silver standard is a monetary system in which the standard economic unit of account is a fixed weight of silver. The silver standard is a monetary arrangement in which a country’s Government allows conversion of its currency into fixed amount of silver.

Question 2.
What is paper currency?
Answer:

1. The paper currency standard refers to the monetary system in which the paper currency notes issued by the Treasury or the Central Bank or both circulate as unlimited legal tender.
2. The paper standard is also known as managed currency standard.
3. The quantity of money in circulation is controlled by the monetary authority to maintain price stability.

Question 3.
Name the main functions of money?
Answer:

Question 4.
Write RBI publishes information alternative measures of money supply?
Answer:
RBI publishes information for four alternative measures of Money supply, namely M₂ , M₂ and M₃ and M₄
M₁ = Currency, coins and demand deposits
M₂ = M₁ + Savings deposits with post office savings banks
M₃ = M₂ + Time deposits of all commercial and cooperative banks.
M₄ = M₃ + Total deposits with Post offices.

Question 5.
Define “Currency symbol”?
Answer:
Currency Symbol ₹
The new symbol designed by D.Udaya Kumar, a post graduate of IIT Bombay was finally selected by the Union cabinet on 15th July, 2010. The new symbol, is an amalgamation of Devanagri ‘Ra’ and the Roman ‘R’ without the stem. The symbol of India rupee came into use on 15th July, 2010. After America, Britain, Japan, Europe Union. India is the 5th country to accept a unique currency symbol.

Question 6.
Write Fisher’s Quantity Theory of money equation?
Answer:

1. The general form of equation given by Fisher is MV = PT.
2. Fisher points out that in a country during any given period of time, the total quantity of money (MV) will be equal to the total value of all goods and services bought and sold (PT).
3. MV = PT

Question 7.
Define “Trade cycle”?
Answer:
“A trade cycle is composed of periods of good trade characterised by rising prices and low unemployment percentages altering with periods of bad trade characterised by falling prices and high unemployment percentages”.

Part – C
Answer The Following Questions In One Paragraph.

Question 1.
Write the meaning of Money supply?
Answer:
Meaning of Money Supply

1. In India, currency notes are issued by the Reserve Bank of India (RBI) and coins are issued by the Ministry of Finance, Government of India (GOI).
2. Besides these, the balance is savings, or current account deposits, held by the public in commercial banks is also considered money.
3. The currency notes are also called fiat money and legal tenders.

Question 2.
Explain the Deflation?
Answer:
Deflation:

1. The essential feature of deflation is falling prices, reduced money supply and unemployment.
2. Though falling prices are desirable at the time of inflation, such a fall should not lead to the fall in the level of production and employment.
3. But if prices fall from the level of full employment both income and employment will be adversely affected.

Question 3.
What is the meaning of trade cycle?
Answer:
Meaning of Trade Cycle:

1. A Trade cycle refers to oscillations in aggregate economic activity particularly in employment, output, income, etc.
2. It is due to the inherent contraction and expansion of the elements which energize the economic activities of the nation.
3. The fluctuations are periodical, differing in intensity and changing in its coverage.

Question 4.
Explain the Evolution of money?
Answer:
Barter System:

1. The introduction of money as a medium of exchange was orje of the greatest inventions of mankind.
2. Before money was invented, exchange took place by Barter, that is, commodities and services were directly exchanged for other commodities and services.
3. Under the barter system, buyers and sellers of commodities had to face a number of difficulties.
4. Surplus goods were exchanged for money which in turn was exchanged for other needed goods.
5. Goods like furs, skins, salt, rice, wheat, utensils, weapons, etc. were commonly used as money.
6. Such exchange of goods for goods was known as “Barter Exchange” or “Barter System”.

Question 5.
What is the meaning of Crypto currency?
Answer:
Crypto Currency:

1. A digital currency in which encryption techniques are used to regulate the generation of units of currency and verify the transfer of funds, operating independently of a Central Bank.
2. Decentralised crypto currencies such as Bitcoin now provide an outlet for Personal Wealth that is beyond restriction and confiscation.

Question 6.
Explain the Trade cycle Depression?
Answer:
Depression:

1. During depression the level of economic activity becomes extremely low.
2. Firms incur losses and closure of business becomes a common feature and the ultimate result is unemployment.
3. Interest prices, profits and wages are low.
4. The agricultural class and wage earners would be worst hit.
5. Banking institutions will be reluctant to advance loans to businessmen.
6. Depression is the worst phase of the business cycle.
7. Extreme point of depression is called as “trough”, because it is a deep point in business cycle.
8. Any person fell down in deeps could not come out from that without other’s help.
9. Similarly, an economy fell down in trough could not come out from this without external help.
10. Keynes advocated that autonomous investment of the government alone can help the economy to come out from the depression.

Part – D
Answer The Following Questions In One Page.

Question 1.
Explain the Measures of control inflation?
Answer:
Measures to Control Inflation:
Keynes and Milton Friedman together suggested three measures to prevent and control of inflation.

1. Monetary measures
2. Fiscal measures (J.M. Keynes) and
3. Other measures.

1. Monetary Measures:

1. These measures are adopted by the Central Bank of the country.
2. They are
   • Increase in Bankrate
   • Sale of Government Securities in the Open Market
   • Higher Cash Reserve Ratio (CRR) and Statutory Liquidity Ratio (SLR)
   • Consumer Credit Control and
   • Higher margin requirements
   • Higher Repo Rate and Reverse Repo Rate.

2. Fiscal Measures:

1. Fiscal policy is now recognized as an important instrument to tackle an inflationary situation.
2. The major anti – inflationary fiscal measures are the following:
   Reduction of Government Expenditure and Public Borrowing and Enhancing taxation.

3. Other Measures:
These measures can be divided broadly into short – term and long – term measures.

(a) Short – term measures can be in regard to public distribution of scarce essential commodities through fair price shops (Rationing). In India whenever shortage of basic goods has been felt, the government has resorted to import so that inflation may not get triggered.

(b) Long – term measures will require accelerating economic growth especially of the wage goods which have a direct bearing on the general price and the cost of living. Some restrictions on present consumption may help in improving saving and investment which may be necessary for accelerating the rate of economic growth in the long run.

Question 2.
Briefly explain the Monetary Economics and money?
Answer:

1. Monetary Economics is a branch of economics that provides a framework for analyzing money and its functions as a medium of exchange, store of value and unit of account.
2. It examines the effects of monetary systems including regulation of money and associated financial institutions.
   Meaning
3. Money is anything that is generally accepted as payment for goods and services and repayment of debts and that serves as a medium of exchange.
4. A medium of exchange is anything that is widely accepted as a means of payments.
5. In recent years, the importance of credit has increased in all the countries of the world.
6. Credit instruments are used on an extensive scale.
7. The use of cheques, bills of exchange, etc. has gone up.
8. It should however, be remembered that money is the basis of credit.

Question 3.
Explain the Inflation Effects of production?
Answer:
Effects on Production: When the inflation is very moderate, it acts as an incentive to traders and producers. This is particularly prior to full employment when resources are not fully utilized. The profit due to rising prices encourages and induces business class to increase their investments in production, leading to generation of employment and income.

1. However, hyper – inflation results in a serious depreciation of the value of money and it discourages savings on the part of the public.

2. When the value of money undergoes considerable depreciation, this may even drain out the foreign capital already invested in the country.

3. With reduced capital accumulation, the investment will suffer a serious set – back which may have an adverse effect on the volume of production in the country. This may discourage entrepreneurs and business men from taking business risk.

4. Inflation also leads to hoarding of essential goods both by the traders as well as the consumers and thus leading to still higher inflation rate.

5. Inflation encourages investment in speculative activities rather than productive purposes.

Students can Download Economics Chapter 4 Consumption and Investment Functions Questions and Answers, Notes Pdf, Samacheer Kalvi 12th Economics Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 4 Consumption and Investment Functions

Samacheer Kalvi 12th Economics Consumption and Investment Functions Text Book Back Questions and Answers

Part – A
Multiple Choice Questions.

Question 1.
The average propensity to consume is measured by –
(a) C / Y
(b) C × Y
(c) Y / C
(d) C + Y
Answer:
(a) C / Y

Question 2.
An increase in the marginal propensity to consume will:
(a) Lead to consumption function becoming steeper
(b) Shift the consumption function upwards
(c) Shift the consumption function downwards
(d) Shift savings function upwards
Answer:
(a) Lead to consumption function becoming steeper.

Question 3.
If the Keynesian consumption function is C = 10 + 0.8 Y then, if disposable income is Rs 1000, what is amount of total consumption?
(a) ₹ 0.8
(b) ₹ 800
(c) ₹ 810
(d) ₹ 0.81
Answer:
(c) ₹ 810

Question 4.
If the Keynesian consumption function is C = 10 + 0.8 Y then, when disposable income is Rs 100, what is the marginal propensity to consume?
(a) ₹ 0.8
(b) ₹ 800
(c) ₹ 810
(d) ₹ 0.81
Answer:
(a) ₹ 0.8

Question 5.
If the Keynesian consumption function is C = 10 + 0.8 Y then, and disposable income is ₹ 100, what is the average propensity to consume?
(a) ₹ 0.8
(b) ₹ 800
(c) ₹ 810
(d) ₹ 0.9
Answer:
(d) ₹ 0.9

Question 6.
As national income increases –
(a) The APC falls and gets nearer in value to the MPC.
(b) The APC increases and diverges in value from the MPC.
(c) The APC stays constant
(d) The APC always approaches infinity.
Answer:
(a) The APC falls and gets nearer in value to the MPC.

Question 7.
As increase in consumption at any given level of income is likely to lead –
(a) Higher aggregate demand
(b) An increase in exports
(c) A fall in taxation revenue
(d) A decrease in import spending
Answer:
(a) Higher aggregate demand

Question 8.
Lower interest rates are likely to:
(a) Decrease in consumption
(b) increase cost of borrowing
(c) Encourage saving
(d) increase borrowing and spending
Answer:
(d) increase borrowing and spending

Question 9.
The MPC is equal to:
(a) Total spending / total consumption
(b) Total consumption / total income
(c) Change in consumption / change in income
(d) None of the above
Answer:
(c) Change in consumption / change in income

Question 10.
The relationship between total spending on consumption and the total income is the –
(a) Consumption function
(b) Savings function
(c) Investment function
(d) aggregate demand function
Answer:
(a) Consumption function

Question 11.
The sum of the MPC and MPS is –
(a) 1
(b) 2
(c) 0.1
(d) 1.1
Answer:
(a) 1

Question 12.
As income increases, consumption will –
(a) fall
(b) not change
(c) fluctuate
(d) increase
Answer:
(d) increase

Question 13.
When investment is assumed autonomous the slope of the AD schedule is determined by the –
(a) marginal propensity to invest
(b) disposable income
(c) marginal propensity to consume
(d) average propensity to consume
Answer:
(c) marginal propensity to consume

Question 14.
The multiplier tells us how much changes after a shift in –
(a) Consumption, income
(b) investment, output
(c) savings, investment
(d) output, aggregate demand
Answer:
(d) output, aggregate demand

Question 15.
The multiplier is calculated as –
(a) 1 / (1 – MPC)
(b) 1 / MPS
(c) 1 / MPC
(d) a and b
Answer:
(d) a and b

Question 16.
It the MPC is 0.5, the multiplier is –
(a) 2
(b) 1/2
(c) 0.2
(d) 20
Answer:
(a) 2

Question 17.
In an open economy import ………………………. the value of the multiplier
(a) Reduces
(b) increase
(c) does not change
(d) changes
Answer:
(a) Reduces

Question 18.
According to Keynes, investment is a function of the MEC and –
(a) Demand
(b) Supply
(c) Income
(d) Rate of interest
Answer:
(d) Rate of interest

Question 19.
The term super multiplier was first used by –
(a) J.R.Hicks
(b) R.G.D. Allen
(c) Kahn
(d) Keynes
Answer:
(a) J.R.Hicks

Question 20.
The term MEC was introduced by –
(a) Adam Smith
(b) J.M. Keynes
(c) Ricardo
(d) Malthus
Answer:
(b) J.M. Keynes

Part – B
Answer The Following Questions In One or Two Sentences

Question 21.
What is consumption function?
Answer:
Meaning of Consumption Function:

1. The consumption function or propensity to consume refers to income consumption relationship. It is a “functional relationship between two aggregates viz., total consumption and gross national income.”

2. Symbolically, the relationship is represented as C = f (Y)
Where,
C = Consumption; Y = Income; f = Function

3. Thus the consumption function indicates a functional relationship between C and Y, where C is the dependent variable and Y is the independent variable, i.e., C is determined by Y. This relationship is based on the ceteris paribus (other things being same) assumption, as only income consumption relationship is considered and all possible influences on consumption are held constant.

Question 22.
What do you mean by propensity to consume?
Answer:

1. The consumption function or propensity to consume refers to income consumption relationship. It is a “functional relationship between two aggregates viz., total consumption and gross national income.”

2. Symbolically, the relationship is represented as C = f(Y) Where, C = Consumption; Y = Income; f = Function

3. Thus the consumption function indicates a functional relationship between C and Y, where C is the dependent variable and Y is the independent variable, i.e., C is determined by Y. This relationship is based on the ceteris paribus (other things being same) assumption, as only income consumption relationship is considered and all possible influences on consumption are held constant.

Question 23.
Define average propensity to consume (APC)?
Answer:
Average Propensity to Consume:

1. The average propensity to consume is the ratio of consumption expenditure to any particular level of income.” Algebraically it may be expressed as under:
Where, C = Consumption; Y = Income
APC = \(\frac{C}{Y}\)
Where, C = Consumption; Y = Income.

Question 24.
Define marginal propensity to consume (MPC)?
Answer:
Marginal Propensity to Consume:

1. The marginal propensity to consume may be defined as the ratio of the change in the consumption to the change in income. Algebraically it may be expressed as under:
MPC = \(\frac { \Delta C }{ \Delta Y } \)
Where, ∆C = Change in Consumption; ∆Y = Change in Income
MPC is positive but less than unity, 0 < \(\frac { \Delta C }{ \Delta Y } \) < 1.

Question 25.
What do you mean by propensity to save?
Answer:

1. Thus the consumption function measures not only the amount spent on consumption but also the amount saved.
2. This is because the propensity to save is merely the propensity not to consume.
3. The 45° line may therefore be regarded as a zero – saving line, and the shape and position of the C curve indicate the division of income between consumption and saving.

Question 26.
Define average propensity to save (APS)?
Answer:
Average Propensity to Save (APS):

1. The average propensity to save is the ratio of saving to income.
2. APS is the quotient obtained by dividing the total saving by the total income. In other words, it is the ratio of total savings to total income. It can be expressed algebraically in the form of equation as under
3. APS = \(\frac{S}{Y}\) Where, S = Saving; Y = Income

Question 27.
Define Marginal Propensity to Save (MPS)?
Answer:
Marginal Propensity to Save (MPS):

1. Marginal Propensity to Save is the ratio of change in saving to a change in income.

2. MPS is obtained by dividing change in savings by change in income. It can be expressed algebraically as MPS = \(\frac { \Delta S }{ \Delta Y } \)
∆S = Change in Saving; ∆Y = Change in Income
Since MPC + MPS = 1
MPS = 1 – MPC and MPC = 1 – MPS.

Question 28.
Define Multiplier?
Answer:

1. The multiplier is defined as the ratio of the change in national income to change in investment.
2. If AI stands for increase in investment and AY stands for resultant increase in income, the multiplier K =AY/AI.
3. Since AY results from AI, the multiplier is called investment multiplier.

Question 29.
Define Accelerator?
Answer:

1. “The accelerator coefficient is the ratio between induced investment and an initial change in consumption.”
2. Assuming the expenditure of ₹50 crores on consumption goods, if industries lead to an investment of ₹100 crores in investment goods industries, we can say that the accelerator is 2.
3. Accelerator = \(\frac { 100 }{ \Delta Y } \) = 2

Part – C
Answer The Following Questions In One Paragraph.

Question 30.
State the propositions of Keynes’s Psychological Law of Consumption?
Answer:
Propositions of the Law:
This law has three propositions:
1. When income increases, consumption expenditure also increases but by a smaller amount. The reason is that as income increases, we wants are satisfied side by side, so that the need to spend more on consumer goods diminishes. So, the consumption expenditure increases with increase in income but less than proportionately.

2. The increased income will be divided in some proportion between consumption expenditure and saving. This follows from the first proposition because when the whole • of increased income is not spent on consumption, the remaining is saved. In this way, consumption and saving move together.

3. Increase in income always leads to an increase in both consumption and saving. This means that increased income is unlikely to lead to fall in either consumption or saving. Thus with increased income both consumption and saving increase.

Question 31.
Differentiate autonomous and induced investment?
Answer:
Autonomous Investment:

1. Independent
2. Income inelastic
3. Welfare motive

Induced Investment:

1. Planned
2. Income elastic
3. Profit Motive

Question 32.
Explain any three subjective and objective factors influencing the consumption function?
Answer:
Subjective Factors:

1. The motive of precaution: To build up a reserve against unforeseen contingencies. e.g. Accidents, sickness. ,
2. The motive of foresight: The desire to provide for anticipated future needs. e.g. Old age.
3. The motive of calculation: The desire to enjoy interest and appreciation. Consumption and Investment Functions.

Objective Factors:
1. Income Distribution:
If there is large disparity between rich and poor, the consumption is low because the rich people have low propensity to consume and high propensity to save.

2. Price level:
Price level plays an important role in determining the consumption function. When the price falls, real income goes up; people will consume more and propensity to save of the
society increases.

3. Wage level:
Wage level plays an important role in determining the consumption function and there is positive relationship between wage and consumption. Consumption expenditure increases with the rise in wages. Similar is the effect with regard to windfall gains.

Question 33.
Mention the differences between accelerator and multiplier effect?
Answer:
Accelerator Effect Multiplier Effect:

1. Accelerator is the numerical value of the relation between an increase in consumption and the resulting increasing in Investment. Multiplier is the ration of the change in national income to change in Investment.

2. Accelerator (β) = \(\frac { \Delta I }{ \Delta C } \)
ΔI = Change in Investment
ΔC = Change in consumption demand Multiplier (K) = \(\frac { \Delta I }{ \Delta C } \)
ΔI = Increase in Investment ΔY = Increase in Income ΔY results from ΔI

3. Accelerator Effects are –

1. Increase in consumer demand.
2. Films get close to fill capacity.
3. Film invest to meet rising demand. Multiplier Effects are

Multiplier Effect:
1. Multiplier is the ration of the change in national income to change in Investment.

2. Multiplier:
Multiplier (K) = \(\frac { \Delta Y }{ \Delta I } \)
ΔI = Increase in Investment
ΔY = Increase in Income
ΔY results from ΔI

Multiplier Effects are:

1. Positive Multiplier an initial increases is an injection (or a decrease in a leakage) leads to a greater final increase in real GDP.
2. Negative Multiplier an initial increases in an injection (or an increase in a leakage) leads to a greater final decrease in real GDP.

Question 34.
State the concept of super multiplier?
Answer:
Super Multiplier: (k and β interaction):

1. The super multiplier is greater than simple multiplier which includes only autonomous investment and no induced investment, while super multiplier includes induced investment.
2. In order to measure the total effect of initial investment on income, Hicks has combined the k and β mathematically and given it the name of the Super Multiplier.
3. The super multiplier is worked out by combining both induced consumption and induced investment.

Question 35.
Specify the limitations of the multiplier?
Answer:

1. There is change in autonomous investment.
2. There is no induced investment
3. The marginal propensity to consume is constant.
4. Consumption is a function of current income.
5. There are no time lags in the multiplier process.
6. Consumer goods are available in response to effective demand for them.
7. There is a closed economy unaffected by foreign influences.
8. There are no changes in prices.
9. There is less than full employment level in the economy.

Part – D
Answer The Following Questions In About A Page.

Question 36.
Explain Keynes psychological law of consumption function with diagram?
The three propositions of the law:

Proposition (1):
Income increases by ₹ 60 crores and the increase in consumption is by ₹ 50 crores.

Proposition (2):
The increased income of ₹ 60 crores in each case is divided in some proportion between consumption and saving respectively, (i.e., ₹ 50 crores and ₹ 10 crores).

Proposition (3):
As income increases consumption as well as saving increase. Neither consumption nor saving has fallen. Diagrammatically, the three propositions are explained in figure. Here, income is measured horizontally and consumption and saving are measured on the vertical axis. C is the consumption function curve and 45° line represents income consumption equality.

Proposition (1):
When income increases from 120 to 180 consumption also increases from 120 to 170 but the increase in consumption is less than the increase in income, 10 is saved.

Proposition (2):
When income increases to 180 and 240, it is divided in some proportion between consumption by 170 and 220 and saving by 10 and 20 respectively.

Proposition (3):
Increases in income to 180 and 240 lead to increased consumption 170 and 220 and increased saving 20 and 10 than before. It is clear from the widening area below the C curve and the saving gap between 45° line and C curve.

Question 37.
Briefly explain the subjective and objective factors of consumption function?
Answer:
Subjective Factors:

1. The motive of precaution: To build up a reserve against unforeseen contingencies. e.g. Accidents, sickness
2. The motive of foresight: The desire to provide for anticipated future needs, e.g. Old age
3. The motive of calculation: The desire to enjoy interest and appreciation.
4. The motive of improvement: The desire to enjoy for improving standard of living.
5. The motive of financial independence.
6. The motive of enterprise (desire to do forward trading).
7. The motive of pride.(desire to bequeath a fortune)
8. The motive of avarice.(purely miserly instinct)

Objective Factors:
1. Income Distribution:
If there is large disparity between rich and poor, the consumption is low because the rich people have low propensity to consume and high propensity to save.

2. Price level:

1. Price level plays an important role in determining the consumption function.
2. When the price falls, real income goes up; people will consume more and propensity to save of the society increases.

3. Wage level:

1. Wage level plays an important role in determining the consumption function and there is positive relationship between wage and consumption.
2. Consumption expenditure increases with the rise in wages.
3. Similar is the effect with regard to windfall gains.

4. Interest rate:

1. Rate of interest plays an important role in determining the consumption function.
2. Higher rate of interest will encourage people to save more money and reduces consumption.

5. Fiscal Policy:
When government reduces the tax the disposable income rises and the propensity to consume of community increases.

6. Consumer credit:

1. The availability of consumer credit at easy installments will encourage households to buy consumer durables like automobiles, fridge, computer.
2. This pushes up consumption.

7. Demographic factors:

1. Ceteris paribus, the larger the size of the family, the grater is the consumption.
2. Besides size of family, stage in family life cycle, place of residence and occupation affect the consumption function.

8. Duesenberry hypothesis:
Duesenberry has made two observations regarding the factors affecting consumption.

1. The consumption expenditure depends not only on his current income but also past income and standard of living.
2. Consumption is influenced by demonstration effect. The consumption standards of low income groups are influenced by the consumption standards of high income groups.

9. Windfall Gains or losses:
Unexpected changes in the stock market leading to gains or losses tend to shift the consumption function upward or downward.

Question 38.
Illustrate the working of Multiplier?
Answer:
Working of Multiplier:

1. Suppose the Government undertakes investment expenditure equal to ₹ 100 crore on some public works, by way of wages, price of materials etc.
2. Thus income of labourers and suppliers of materials increases by ₹ 100 crore. Suppose the MPC is 0.8 that is 80 %.
3. A sum of ₹ 80 crores is spent on consumption (A sum of ₹ 20 Crores is saved).
4. As a result, suppliers of goods get an income of ₹ 80 crores.
5. They intum spend ₹ 64 crores (80% of ₹ 80 cr).
6. In this manner consumption expenditure and increase in income act in a chain like maimer.

The final result is ∆Y = 100 + 100 × 4/5 + 100 × [4/5]² + 100 × [4/5]³ or,
∆Y = 100 + 100 × 0.8 + 100 × (0.8)² + 100 × (0.8)³
= 100 + 80 + 64 + 51.2… = 500 .
that is 100 × 1/1 – 4/5
100 × 1/1/5
100 × 5 = ₹ 500 crores
For instance if C = 100 + 0.8Y, I = 100,
Then Y = 100 + 0.8Y + 100
0.2Y = 200
Y = 200/0.2 = 1000 → Point B
If I is increased to 110, then
0.2Y = 210
Y = 210/0.2 = 1050 → Point D
For ₹ 10 increase in I, Y has increased by ₹ 50.
This is due to multiplier effect.
At point A, Y = C = 500
C = 100 + 0.8 (500) = 500; S = 0
At point B, Y = 1000
C = 100 + 0.8 (1000) = 900; S = 100 = I At point D, Y = 1050
C = 100 + 0.8 (1050) = 940; S = 110 = I
When I is increased by 10, Y increases by 50.
This is multiplier effect (K = 5)
K = \(\frac{1}{0.2}\) = 5

Question 39.
Explain the operation of the Accelerator?
Answer:
Operation of the Acceleration Principle:

1. Let us consider a simple example. The operation of the accelerator may be illustrated as follows.
2. Let us suppose that in order to produce 1000 consumer goods, 100 machines are required.
3. Also suppose that working life of a machine is 10 years.
4. This means that every year 10 machines have to be replaced in order to maintain the constant flow of 1000 consumer goods. This might be called replacement demand.
5. Suppose that demand for consumer goods rises by 10 percent (i.e. from 1000 to 1100).
6. This results in increase in demand for 10 more machines.
7. So that total demand for machines is 20. (10 for replacement and 10 for meeting increased demand).
8. It may be noted here a 10 percent increase in demand for consumer goods causes a 100 percent increase in demand for machines (from 10 to 20).
9. So we can conclude even a mild change in demand for consumer goods will lead to wide change in investment.

Diagrammatic illustration:
Operation of Accelerator.

1. SS is the saving curve. II is the investment curve. At point E₁ the economy is in equilibrium with OY₁ income. Saving and investment are equal at OY₁ Now, investment is increased from OI₂ to OI₄.
2. This increases income from OY₁ to OY₃, the equilibrium point being E₃ If the increase in investment by I₂ I₄ is purely exogenous, then the increase in income by Y₁ Y₃ would have been due to the multiplier effect.
3. But in this diagram it is assumed that exogenous investment is only by I, I3 and induced investment is by I₃I₄.
4. Therefore, increase in income by Y₁ Y₂ is due to the multiplier effect and the increase in income by Y₂ Y₃ is due to the accelerator effect.

Question 40.
What are the differences between MEC and MEI?
Answer:
Marginal Efficiency of Capital (MEC):

1. It is based on a given supply price for capital.
2. It represents the rate of return on all successive units of capital without regard to existing capital.
3. The capital stock is taken on the X axis of diagram.
4. It is a “stock” concept.
5. It determines the optimum capital stock in an economy at each level of interest rate.

Marginal Efficiency of Investment (MEI):

1. It is based on the induced change in the price due to change in the demand for capital.
2. It shows the rate of return on just those units of capital over and above the existing capital stock.
3. The amount of investment is taken on the X – axis of diagram.
4. It is a “flow” concept.
5. It determines the net investment of the economy at each interest rate given the capital stock.

Samacheer Kalvi 12th Economics Consumption and Investment Functions Additional Questions and Answers

part – A
I. Multiple Choice Questions.

Question 1.
Price level plays an important role in determining the ……………………
(a) Consumption function
(b) Income function
(c) Finance function
(d) Price function
Answer:
(a) Consumption function

Question 2.
The progressive tax system increases the ……………………….. of the people by altering the income distribution in favour of poor?
(a) price level
(b) wage level
(c) propensity to consume
(d) Fiscal policy
Answer:
(c) propensity to consume

Question 3.
…………………….. means purchase of stocks and shares, debentures, government bonds and equities?
(a) Consumption
(b) Investment
(c) Finance
(d) Saving
Answer:
(b) Investment

Question 4.
…………………… is influenced by demonstration effect.
(a) Investment
(b) Interest
(c) Expenditure
(d) Consumption
Answer:
(d) Consumption

Question 5.
Additional investment that is independent of income is called ……………………
(a) Autonomous Investment
(b) Autonomous Consumption
(c) Average Investment
(d) Marginal Investment
Answer:
(a) Autonomous Investment

Question 6.
Induced investment is motivated?
(a) Investment
(b) Capital
(c) Saving
(d) Profit
Answer:
(d) Profit

Question 7.
MEI is the expected rate of return on investment as additional units of ……………………
(a) Saving
(b) Investment
(c) Consumption
(d) Expenditure
Answer:
(b) Investment

Question 8.
Dynamic multiplier is also known as ……………………
(a) Sequence multiplier
(b) Static multiplier
(c) Double multiplier
(d) Single multiplier
Answer:
(a) Sequence multiplier

Question 9.
The combined effect of interaction of multiplier and accelerator is called ……………………
(a) Super accelerator
(b) Super multiplier
(c) Accelerator
(d) Multiplier
Answer:
(b) Super multiplier

Question 10.
The tendency to initiate Superior consumption pattern is called ……………………
(a) Accelerator effect
(b) Multiplier effect
(c) Super Multiplier effect
(d) Demonstration effect
Answer:
(d) Demonstration effect

Question 11.
The multiplier is the reciprocal of one minus ……………………
(a) MPC
(b) MPS
(c) Multiplier
(d) Accelerator
Answer:
(a) MPC

Question 12.
The concept of multiplier was first developed by ……………………
(a) J.M. Keynes
(b) David Ricardo
(c) R.F. Khan
(d) J.B. Say
Answer:
(c) R.F. Khan

Question 13.
…………………… the larger size of the family, the greater is the consumption?
(a) Demographic factors
(b) Income Distribution
(c) Duesenberry hypothesis
(d) Wage level
Answer:
(b) Income Distribution

Question 14.
MPS is the ratio of change in saving to a change in ……………………
(a) profit
(b) money
(c) finance
(d) income
Answer:
(d) income

Question 15.
Consumption function is called the relationship between ……………………….. and Income?
(a) Money
(b) Consumption
(c) Finance
(d) Investment
Answer:
(b) Consumption

Question 16.
Consumer’s surplus is useful to the Finance Minister in formulating ……………………….. policies?
(a) Surplus
(b) Consumption
(c) Taxation
(d) Income
Answer:
(c) Taxation

Question 17.
Consumer surplus is called potential price – ……………………………. price?
(a) real
(b) actual
(c) normal
(d) high
Answer:
(b) actual

Question 18.
Dynamic multiplier is also known as ………………………. Multiplier.
(a) Sequence
(b) Static
(c) Timeless
(d) Logical
Answer:
(a) Sequence

Question 19.
Static Multiplier is otherwise known as …………………………… Multiplier.
(a) Dynamic
(b) Leakage
(c) Simultaneous
(d) Multi effect
Answer:
(c) Simultaneous

Question 20.
The propensity to consume refers to the portion of Income spent on ……………………….
(a) Income
(b) Profit
(c) Expenditure
(d) Consumption
Answer:
(d) Consumption

Question 21.
………………………. redefined it as investment multiplier.
(a) R.K. Khan
(b) David Ricardo
(c) J.M. Keynes
(d) Marshall
Answer:
(c) J.M. Keynes

Question 22.
Accelerator Model was made by ……………………
(a) J.M. Keynes
(b) J.M. Clark
(c) R.F. Khan
(d) Marshall
Answer:
(b) J.M. Clark

Question 23.
The multiplier tells us …………………………. changes after a shift in ……………………
(a) income
(b) investment
(c) aggregate demand
(d) savings
Answer:
(c) aggregate demand

Question 24.
The simple accelerated model was made by J.M. Clark in ……………………
(a) 1915
(b) 1916
(c) 1914
(d) 1917
Answer:
(d) 1917

II. Match the following and choose the correct answer by using codes given below

Question 1.
A. Consumption function – (i) Consmption increased
B. Induced Investment – (ii) Borrowings
C. Income Increases – (iii) Subjective and objective
D. Autonomous consumption – (iv) Profit motive
Codes:
(a) A (iii) B (iv) C (i) D (ii)
(b) A (iv) B (i) C (ii) D (iii)
(c) A (i) B (ii) C (iii) D (iv)
(d) A (ii) B (iii) C (iv) D (i)
Answer:
(a) A (iii) B (iv) C (i) D (ii)

Question 2.
A. MPS – measured – (i) K = 1/MPS
B. Multiplier developed by – (ii) MEC
C. Investment depends on – (iii) ∆S/∆Y
D. Value of multiplier – (iv) R.F. Khan
Codes:
(a) A (i) B (ii) C (iv) D (iii)
(b) A (ii) B (iii) C (i) D (iv)
(c) A (iii) B (iv) C (ii) D (i)
(d) A (iv) B (i) C (iii) D (ii)
Answer:
(c) A (iii) B (iv) C (ii) D (i)

Question 3.
A. Reduced Investment – (i) 1930
B. Keynes employment dependes on – (ii) Highest interest rate
C. Fall in investment – (iii) Zero
D. Long fun autonomous consumption will – (iv) Investment
Codes:
(a) A (i) B (iii) C (iv) D (ii)
(b) A (ii) B (iv) C (i) D (iii)
(c) A (iii) B (i) C (ii) D (iv)
(d) A (iv) B (ii) C (iii) D (i)
Answer:
(b) A (ii) B (iv) C (i) D (iii)

Question 4.
A. MPS – (i) AC/AY
B. MPC – (ii) C/Y
C. APS – (iii) S/Y
D. APC – (iv) AS/AY
Codes:
(a) A (iv) B (i) C (iii) D (ii)
(b) A (i) B (ii) C (iv) D (iii)
(c) A (ii) B (iii) C (i) D (iv)
(d) A (iii) B (iv) C (ii) D (i)
Answer:
(a) A (iv) B (i) C (iii) D (ii)

Question 5.
A. Investment means – (i) Expenditure on capital formation
B. Uses of multiplier – (ii) Consumption forgone
C. Saving is – (iii) Achieve full employment
D. Autonomous investment – (iv) Stocks and shares
Codes:
(a) A (ii) B (i) C (iv) D (iii)
(b) A (iii) B (ii) C (iii) D (iv)
(c) A (iv) B (iii) C (ii) D (i)
(d) A (i) B (iv) C (i) D (ii)
Answer:
(c) A (iv) B (iii) C (ii) D (i)

III. State whether the statements are true or false.

Question 1.
(i) Keynes propounded the fundamental psychological law of consumption.
(ii) J.M. Keynes has divided factors influencing the consumption function.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 2.
(i) The kinds of multiplier is called Tax Multiplier, Employment Multiplier, Foreign trade Multiplier, Investment Multiplier.
(ii) Investment means money collecting.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(d) (i) is false but (ii) is true

Question 3.
(i) The term investment means purchase of stocks and shares, debentures, government bonds and equities.
(ii) The term Investment means expenditure on capital formation.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 4.
(i) Leakages of multiplier is payment only.
(ii) Leakages of multiplier limitation is called full employment situation.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(d) (i) is false but (ii) is true

Question 5.
(i) The types of Investment is called Autonomous Investment, Induced Investment.
(ii) Induced Investment is the expenditure on fixed assets and stocks.

(a) Both (i) and (ii) are true
(b) Both 0) and (if) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

IV. Which of the following is correctly matched:

Question 1.
(a) J.M. Clark – Ceteris Paribus
(b) J.M. Keynes – Psychological law of consumption
(c) R.F. Khan – Accelerator model
(d) Duesenberry – Laissez – faire
Answer:
(b) J.M. Keynes – Psychological law of consumption

Question 2.
(a) Induced Investment – Profit motive
(b) MEC – Autonomous Investment
(c) MEI – Technology
(d) MPC – Accelerator
Answer:
(a) Induced Investment – Profit motive

Question 3.
(a) Dynamic Multiplier – Employment
(b) Static Multiplier – Wealth
(c) Accelerator Model – J.M. Clark
(d) Leakage Multiplier – Investment goods
Answer:
(c) Accelerator Model – J.M. Clark

Question 4.
(a) Afltalion – 1909
(b) Hawtrey – 1914
(c) Bickerdike – 1915
(d) J.M. Clark – 1916
Answer:
(a) Afltalion – 1909

Question 5.
(a) Aggregate Income – C
(b) Consumption expenditure – I_A
(c) Autonomous Investment – Y
(d) Induced Private Investment – I_P
Answer:
(d) Induced Private Investment – I_P

V. Which of the following is not correctly matched

Question 1.
(a) Static multiplier – Simultaneous multiplier
(b) Dynamic multiplier – Sequence multiplier
(c) Leakage multiplier – Timeless multiplier
(d) Kinds of multiplier – Tax multiplier
Answer:
(c) Leakage multiplier – Timeless multiplier

Question 2.
(a) Ratio of the consumption – APC expenditure to Income
(b) Ratio of change in consumption – MPC to change in Income
(c) Ratio of the saving to Income – APS
(d) Ratio of change in saving to change in Income – PSM change in Income
Answer:
(d) Ratio of change in saving to change in Income – PSM change in Income

Question 3.
(a) Demonstration Effect – Superior consumption pattern
(b) Subjective factors – Psychological feeling
(c) Objective factors – Real and Measurable
(d) Super multiplier – Investment demand
Answer:
(d) Super multiplier – Investment demand

Question 4.
(a) Average propensity to consume – C/Y
(b) Marginal propensity to consume – AC/AY
(c) Average propensity to consume – S/Y
(d) Marginal propensity to save – AY/AS
Answer:
(d) Marginal propensity to save – AY/AS

Question 5.
(a) The motive of precaution – Accidents, Sickness
{b) The motive of foresight – Old age
(c) The motive of improvement – Improve standard of living
(d) The motive of calculation – Money collecting
Answer:
(d) The motive of calculation – Money collecting

VI. Pick the odd one out.

Question 1.
(a) ∆C – Change in consumption
(b) ∆Y – Change in expenditure
(c) ∆S – Change in saving 4
(d) ∆Y – Change in income
Answer:
(b) ∆Y – Change in expenditure

Question 2.
(a) APC – Algebraically Propensity to Consume
(b) MPC – Marginal Propensity to Consume
(c) APS – Average Propensity to Consume
(d) MPS – Marginal Propensity to Save
Answer:
(a) APC – Algebraically Propensity to Consume

Question 3.
Keynes’s Law is based on the Assumptions.
(a) Ceteris paribus
(b) Existence of Normal conditions
(c) Existence of a Laissez – Faire
(d) Existence of a Technical attributes
Answer:
(d) Existence of a Technical attributes

Question 4.
Investment means
(a) Purchase of stocks and shares
(b) Debentures
(c) Government bonds and equities
(d) Bank amount
Answer:
(d) Bank amount

Question 5.
MEC – Short Run Factors
(a) Supply for the product
(b) Liquid Assets
(c) Sudden changes in Income
(d) Current rate of Investment
Answer:
(a) Supply for the product

VII. Assertion and Reason.

1. Assertion (A): Keynes Law of propositions – when Income increases, consumption expenditure also increases but by a smaller amount.
Reason (R): Keynes Law of propositions – Increase in Income always lead to an increase in both consumption and saving.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 2.
Assertion (A): J.M. Keynes has influencing consumption function into subjective factors are the Internal factors related to psychological feelings.
Reason (R): J.M. Keynes has influencing consumption function into objective factors are Internal factors are not measurable.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 3.
Assertion (A): Autonomous Investment is the expenditure on capital formation.
Reason (R): Autonomous Investment is Independent of the change in Income, rate of Interest or rate of profit.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 4.
Assertion (A): MEC – depends on the Demand yield from a capital asset.
Reason (R): MEC – depends on the Supply price of a capital asset.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Question 5.
Assertion (A): Keynes theory of the Multiplier Assumption is change in autonomous Investment.
Reason (R): Keynes theory of the Multiplier Assumption is no Induced Investment.

(а) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(а) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Part – B
Answer The Following Questions In One or Two Sentences.

Question 1.
Write “Propensity to consume” Equations?
Answer:
(i) The Average Propensity to Consume = \(\frac{c}{y}\)
(ii) The Marginal Propensity to Consume = \(\frac{∆c}{∆y}\)
(iii) The Average Propensity to Save = \(\frac{x}{y}\)
(iv) The Marginal Propensity to Save = \(\frac{∆s}{∆y}\)

Question 2.
Define “Ceteris paribus”?
Answer:
Ceteris paribus (constant extraneous variables):
The other variables such as income distribution, tastes, habits, social customs, price movements, population growth, etc. do not change and consumption depends on income alone.

Question 2.
Define “Laissez-Faire” – Capitalist Economy?
Answer:
Existence of a Laissez – faire Capitalist Economy:
The law operates in a rich capitalist economy where there is no government intervention. People should be free to spend increased income. In the case of regulation of private enterprise and consumption expenditures by the State, the law breaks down.

Question 3.
What do you mean “Windfall Gains” or “Losses”?
Answer:
Windfall Gains or losses:
Unexpected changes in the stock market leading to gains or losses tend to shift the consumption function upward or downward.

Question 4.
Define “Autonomous consumption”?
Answer:
Autonomous Consumption:
Autonomous consumption is the minimum level of consumption or spending that must take place even if a consumer has no disposable income, such as spending for . basic necessities.

Part – C
Answer the Following Questions In One Paragraph.

Question 1.
Explain the Keynes Psychological Law’ of consumption assumptions?
Answer:
Keynes’s Law is based on the following assumptions:
1. Ceteris paribus (constant extraneous variables):
The other variables such as income distribution, tastes, habits, social customs, price movements, population growth, etc. do not change and consumption depends on income alone.

2. Existence of Normal Conditions:

1. The law holds good under normal conditions.
2. If, however, the economy is faced with abnormal and extraordinary circumstances like war, revolution or hyperinflation, the law will not operate.
3. People may spend the whole of increased income on consumption.

3. Existence of a Laissez – faire Capitalist Economy:

1. The law operates in a rich capitalist economy where there is no government intervention.
2. People should be free to spend increased income.
3. In the case of regulation of private enterprise and consumption expenditures by the State, the law breaks down.

Question 2.
Explain the Marginal Efficiency of capital?
Answer:
Marginal Efficiency of Capital:

1. MEC was first introduced by J.M Keynes in 1936 as an important determinant of autonomous investment.
2. The MEC is the expected profitability of an additional capital asset.
3. It may be defined as the highest rate of return over cost expected from the additional unit of capital asset.
4. Meaning of Marginal Efficiency of Capital (MEC) is the rate of discount which makes the discounted present value of expected income stream equal to the cost of capital.

MEC depends on two factors:

1. The prospective yield from a capital asset.
2. The supply price of a capital asset.

Factors Affecting MEC:

Question 3.
Explain the uses of multiplier?
Answer:
Uses of multiplier

1. Multiplier highlights the importance of investment in income and employment theory
2. The process throws light on the different stages of trade cycle.
3. It also helps in bringing the equality between S and I.
4. It helps in formulating Government policies.
5. It helps to reduce unemployment and achieve full employment.

Question 4.
Write the Accelerator Assumptions?
Answer:
Assumptions:

1. Absence of excess capacity in consumer goods industries.
2. Constant capital – output ratio
3. Increase in demand is assumed to be permanent
4. Supply of funds and other inputs is quite elastic
5. Capital goods are perfectly divisible in any required size.

Question 5.
Write the “Leverage Effect” and Equation Explanation?
Answer:
Leverage Effect:
The combined effect of the multiplier and the accelerator is also called the leverage effect which may lead the economy to very high or low level of income propagation.
Symbolically
Y = C + I_A + I_P
Y = Aggregate income
C = Consumption expenditure
T = autonomous investment; I_P = induced private investment

Part – D
Answer The Following Questions In One Page.

Question 1.
Briefly explain the Leakages of Multiplier?
Answer:
Leakages of multiplier:

1. The multiplier assumes that those who earn income are likely to spend a proportion of their additional income on consumption.
2. But in practice, people tend to spend their additional income on other items. Such expenses are known as leakages.

Payment towards past debts:
If a portion of the additional income is used for repayment of old loan, the MPC is reduced and as a result the value of multiplier is cut.

Purchase of existing wealth:

1. If income is used in purchase of existing wealth such as land, building and shares money is circulated among people and never enters into the consumption stream.
2. As a result the value of multiplier is affected.

Import of goods and services:

1. Income spent on imports of goods or services flows out of the country and has little chance to return to income stream in the country.
2. Thus imports reduce the value of multiplier.

Non availability of consumer goods:

1. The multiplier theory assumes instantaneous supply of consumer goods following demand.
2. But there is often a time lag.
3. During this gap (D > S) inflation is likely to rise.
4. This reduces the consumption expenditure and there by multiplier value.

Full employment situation:

1. Under conditions of full employment, resources are almost fully employed.
2. So, additional investment will lead to inflation only, rather than generation of additional real income.

Question 2.
Explain Marginal Propensity to Consume [MPC] and Multiplier with diagram and Diagrammatic explanation?
Answer:
Marginal propensity to consume and multiplier.
The propensity to consume refers to the portion of income spent on consumption.
The MPC refers to the relation between change in consumption (C) and change in income (Y).

Symbolically MPC = ∆C/∆Y
The value of multiplier depends on MPC
Multiplier (K) = 1/1 – MPC
The multiplier is the reciprocal of one minus marginal propensity to consume.
Since marginal propensity to save is 1 – MPC. (MPC + MPS = 1).
Multiplier is 1/ MPS.
The multiplier is therefore defined as reciprocal of MPS.
Multiplier is inversely related to MPS and directly with MPC.
Numerically if MPC is 0.75, MPS is 0.25 and k is 4.
Using formula k = 1/1 – MPC
1/1 – 0.75 = 1/0.25 = 4
Taking the following values, we can explain the functioning of multiplier.

C = 100 + 0.8 y; 1 = 100 1 = 10
Y = C + I
Y = 100 + 0.8y = 100 + (1000) = 900;
S = 100 = I
After I is raised by 10, now I = 110
Y = 100 + 0.8y + 110
0.2y = 210
Y = \(\frac{210}{0.2}\) = 1050
Here C = 100 = 0.8 (1050) = 940; S = 110 = 1
Diagrammatic Explanation.
At 45° line y = C + S
It implies the variables in axis and axis are equal.
The MPC is assumed to be at 0.8 (C = 100 + 0.8y)
The aggregate demand (C + I) curve intersects 45° line at point E.
The original national income is 500.
(C = 100 + 0.8y = 100 + 0.8 (500) = 500)
When I is 100, y = 1000, C = 900;
S = 100 = I
The new aggregate demand curve is C+F = 100 + 0.8y + 100 + 10
Y = \(\frac{210}{0.2}\) = 1050
C = 940; S = 110 = 1

Question 3.
Explain about Marginal Efficiency of Capital [MEC] short run factors and long run factors?
Answer:
(a) Short – Run Factors

1. Demand for the product:

1. If the market for a particular good is expected to grow and its costs are likely to fall, the rate of return from investment will be high.
2. If entrepreneurs expect a fall in demand for goods and a rise in cost, the investment will decline.

2. Liquid assets:

1. If the entrepreneurs are holding large volume of working capital, they can take advantage of the investment opportunities that come in their way.
2. The MEC will be high.

3. Sudden changes in income:

1. The MEC is also influenced by sudden changes in income of the entrepreneurs.
2. If the business community gets windfall profits, or tax concession the MEC will be high and hence investment in the country will go up.
3. On the other hand, MEC falls with the decrease in income.

4. Current rate of investment:

1. Another factor which influences MEC is the current rate of investment in a particular industry.
2. If in a particular industry, much investment has already taken place and the rate of investment currently going on in that industry is also very large, then the marginal efficiency of capital will be low.

5. Waves of optimism and pessimism:

1. The marginal efficiency of capital is also affected by waves of optimism and pessimism in the business cycle.
2. If businessmen are optimistic about future, the MEC will be likely to be high.
3. During periods of pessimism the MEC is under estimated and so will be low.

(b) Long – Run Factors
The long run factors which influence the marginal efficiency of capital are as follows:

1. Rate of growth of population:

1. Marginal efficiency of capital is also influenced by the rate of growth of population.
2. If population is growing at a rapid speed, it is usually believed that the demand of various types of goods will increase.
3. So a rapid rise in the growth of population will increase the marginal efficiency of capital and a slowing down in its rate of growth will discourage investment and thus reduce marginal efficiency of capital.

2. Technological progress:

1. If investment and technological development take place in the industry, the prospects of increase in the net yield brightens up.
2. For example, the development of automobiles in the 20th century has greatly stimulated the rubber industry, the steel and oil industry etc.
3. So we can say that inventions and technological improvements encourage investment in various projects and increase marginal efficiency of capital.

3. Monetary and Fiscal policies:
Cheap money policy and liberal tax policy pave the way for greater profit margin and so MEC is likely to be high.

4. Political environment:
Political stability, smooth administration, maintenance of law and order help to improve MEC.

5. Resource availability:
Cheap and abundant supply of natural resources, efficient labour and stock of capital enhance the MEC.

Students can Download Economics Chapter 6 Banking Questions and Answers, Notes Banking Pdf, Samacheer Kalvi 12th Economics Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 6 Banking

Samacheer Kalvi 12th Economics Banking Text Book Back Questions and Answers

Part – A
Multiple Choice Questions.

Question 1.
A Bank is a …………………………
(a) Financial institution
(b) Corporate
(c) An Industry
(d) Service institutions
Answer:
(a) Financial institution

Question 2.
A Commercial Bank is an institution that provides services …………………………
(a) Accepting deposits
(b) Providing loans
(c) Both a and b
(d) None of the above
Answer:
(c) Both a and b

Question 3.
The Functions of commercial banks are broadly classified into …………………………
(a) Primary Functions
(b) Secondary functions
(c) Other functions
(d) a, b, and c
Answer:
(d) a, b, and c

Question 4.
Bank credit refers to …………………………
(a) Bank Loans
(b) Advances
(c) Bank loans and advances
(d) Borrowings
Answer:
(c) Bank loans and advances

Question 5.
Credit creation means …………………………
(a) Multiplication of loans and advances
(b) Revenue
(c) Expenditure
(d) Debt
Answer:
(a) Multiplication of loans and advances

Question 6.
NBFI does not have …………………………
(a) Banking license
(b) Government approval
(c) Money ministry approval
Answer:
(a) Banking license

Question 7.
Central bank is …………………………….. authority of any country.
(a) Monetary
(b) Fiscal
(c) Wage
(d) National Income
Answer:
(a) Monetary

Question 8.
Who will act as the banker to the Government of India?
(a) SBI
(b) NABARD
(c) ICICI
(d) RBI
Answer:
(d) RBI

Question 9.
Lender of the last resort is one of the functions of …………………………
(a) Central Bank
(b) Commercial banks
(c) Land Development Banks
(d) Co – operative banks
Answer:
(a) Central Bank

Question 10.
Bank Rate means …………………………
(a) Re – discounting the first class securities
(b) Interest rate
(c) Exchange rate
(d) Growth rate
Answer:
(a) Re – discounting the first class securities

Question 11.
Repo Rate means …………………………
(a) Rate at which the Commercial Banks are willing to lend to RBI
(b) Rate at which the RBI is willing to lend to commercial banks
(c) Exchange rate of the foreign bank
(d) Growth rate of the economy
Answer:
(b) Rate at which the RBI is willing to lend to commercial banks

Question 12.
Moral suasion refers …………………………
(a) Optimization
(b) Maximization
(c) Persuasion
(d) Minimization
Answer:
(c) Persuasion

Question 13.
ARDC started functioning from …………………………
(a) June 3, 1963
(b) July 3, 1963
(c) June 1, 1963
(d) July 1, 1963
Answer:
(d) July 1, 1963

Question 14.
NABARD was set up in …………………………
(a) July 1962
(b) July 1972
(c) July 1982
(d) July 1992
Answer:
(c) July 1982

Question 15.
EXIM bank was established in …………………………
(a) June 1982
(b) April 1982
(c) May 1982
(d) March 1982
Answer:
(d) March 1982

Question 16.
The State Financial Corporation Act was passed by …………………………
(a) Government of India
(b) Government of Tamilnadu
(c) Government of Union Territories
(d) Local Government.
Answer:
(a) Government of India

Question 17.
Monetary policy is formulated by …………………………
(a) Co – operative banks
(b) Commercial banks
(c) Central Bank
(d) Foreign banks
Answer:
(c) Central Bank

Question 18.
Online Banking is also known as …………………………
(a) E – Banking
(b) Internet Banking
(c) RTGS
(d) NEFT
Answer:
(b) Internet Banking

Question 19.
Expansions of ATM.
(a) Automated Teller Machine
(b) Adjustment Teller Machine
(c) Automatic Teller mechanism
(d) Any Time Money
Answer:
(a) Automated Teller Machine

Question 20.
2016 Demonetization of currency includes denominations of …………………………
(a) ₹ 500 and ₹ 1000
(b) ₹ 1000 and ₹ 2000
(c) ₹ 200 and ₹ 500
(d) All the above
Answer:
(a) ₹ 500 and ₹ 1000

Part – B
Answer The Following Questions In One or Two Sentences.

Question 21.
Define Commercial banks?
Answer:
Commercial bank refers to a bank, or a division of a large bank, which more specifically deals with deposit and loan services provided to corporations or large/middle-sized business – as opposed to individual members of the public/small business.

Question 22.
What is credit creation?
Answer:

1. Credit Creation means the multiplication of loans and advances.
2. Commercial banks receive deposits from the public and use these deposits to give loans.
3. However, loans offered are many times more than the deposits received by banks.
4. This function of banks is known as ‘Credit Creation’.

Question 23.
Define Central bank?
Answer:

1. A central bank, reserve bank, or monetary authority is an institution that manages a state’s currency, money supply, and interest rates.
2. Central banks also usually oversee the commercial banking system of their respective countries.

Question 24.
Distinguish between CRR and SLR?
Answer:
CRR:

1. The Central Bank controls credit by changing the Cash Reserves Ratio.
2. Commercial Banks have excessive cash reserves on the basis of which they are creating too much of credit, this will be harmful for the larger interest of the economy.
3. So it will raise the cash reserve ratio which the Commercial Banks are required to maintain with the Central Bank.

SLR:

1. Statutory Liquidity Ratio (SLR) is the amount which a bank has to maintain in the form of cash, gold or approved securities.
2. The quantum is specified as some percentage of the total demand and time liabilities.
3. The liabilities of the bank which are payable on demand anytime, and those liabilities which are accruing in one month’s time due to maturity.

Question 25.
Write the meaning of Open market operations?
Answer:

1. In narrow sense, the Central Bank starts the purchase and sale of Government securities in the money market.
2. In Broad Sense, the Central Bank purchases and sells not only Government securities but also other proper eligible securities like bills and securities of private concerns.
3. When the banks and the private individuals purchase these securities they have to make payments for these securities to the Central Bank.

Question 26.
What is rationing of credit?
Answer:

1. This is the oldest method of credit control. Rationing of credit as an instrument of credit control was first used by the Bank of England by the end of the 18th Century.
2. It aims to control and regulate the purposes for which credit is granted by commercial banks.
3. It is generally of two types.

Question 27.
Mention the functions of agriculture credit department?
Answer:
Functions of Agriculture Credit Department:

1. To maintain an expert staff to study all questions on agricultural credit;
2. To provide expert advice to Central and State Government, State Co – operative Banks and other banking activities.
3. To finance the rural sector through eligible institutions engaged in the business of agricultural credit and to co-ordinate their activities.

Part – C
Answer The Following Questions In One Paragraph.

Question 28.
Write the mechanism of credit creation by commercial banks?
Answer:
Mechanism / Technique of Credit Creation by Commercial Banks:

1. Bank credit refers to bank loans and advances.
2. Money is said to be created when the banks, through their lending activities, make a net addition to the total supply of money in the economy.
3. Money is said to be destroyed when the loans are repaid by the borrowers to the banks and consequently the credit already created by the banks is wiped out in the process.
4. Banks have the power to expand or contract demand deposits and they exercise this power through granting more or less loans and advances and acquiring other assets.
5. This power of commercial bank to create deposits through expanding their loans and advances is known as credit creation.

Question 29.
Give a brief note on NBFI?
Answer:
Non – Banking Financial Institution (NBFI):

1. A non – banking financial institution (NBFI) or non-bank financial company (NBFC) is a financial institution that does not have a full banking license or is not supervised by the central bank.

2. The NBFIs do not carry on pure banking business, but they will carry on other financial transactions. They receive deposits and give loans. They mobilize people’s savings and use the funds to finance expenditure on investment activities. In short, they are institutions which undertake borrowing and lending. They operate in both the money and the capital markets.

3. NBFIs can be broadly classified into two categories. Viz.., (1) Stock Exchange; and (2) Other Financial institutions. Under the latter category comes Finance Companies, Finance Corporations, ChitFunds, Building Societies, Issue Houses, Investment Trusts and Unit Trusts and Insurance Companies.

Question 30.
Bring out the methods of credit control?
Answer:
Methods of Credit Control:
I. Quantitative or General Methods:

1. Bank Rate Policy:
The bank rate is the rate at which the Central Bank of a country is prepared to re – discount the first class securities.

2. Open Market Operations:

1. In narrow sense, the Central Bank starts the purchase and sale of Government securities in the money market.
2. In Broad Sense, the Central Bank purchases and sells not only Government securities but also other proper eligible securities like bills and securities of private concerns.

3. Variable Reserve Ratio:
(I) Cash Reserves Ratio:

1. Under this system the Central Bank controls credit by changing the Cash Reserves Ratio.
2. For example, if the Commercial Banks have excessive cash reserves on the basis of which they are creating too much of credit,this will be harmful for the larger interest of the economy.
3. So it will raise the cash reserve ratio which the Commercial Banks are required to maintain with the Central Bank.

(II) Statutory Liquidity Ratio:

1. Statutory Liquidity Ratio (SLR) is the amount which a bank has to maintain securities.
2. The quantum is specified as some percentage of the total demand and time liabilities (i.ethe liabilities of the bank which are payable on demand anytime, and those liabilities which are accruing in one month’s time due to maturity) of a bank.

Question 31.
What are the functions of NABARD?
Answer:
Functions of NABARD:
NABARD has inherited its apex role from RBI i.e, it is performing all the functions performed
by RBI with regard to agricultural credit.

1. NABARD acts as a refinancing institution for all kinds of production and investment credit to agriculture, small-scale industries, cottage and village industries, handicrafts and rural crafts and real artisans and other allied economic activities with a view to promoting integrated rural development.

2. NABARD gives long-term loans (upto 20 Years) to State Government to enable them to subscribe to the share capital of co – operative credit societies.

3. NABARD gives long-term loans to any institution approved by the Central Government or contribute to the share capital or invests in securities of any institution concerned with agriculture and rural development.

4. NABARD has the responsibility of co – ordinating the activities of Central and State Governments, the Planning Commission (now NITI Aayog) and other all India and State level institutions entrusted with the development of small scale industries, village and cottage industries, rural crafts, industries in the tiny and decentralized sectors, etc.

5. It maintains a Research and Development Fund to promote research in agriculture and rural development

Question 32.
Specify the functions of IFCI?
Answer:

1. Long – term loans; both in rupees and foreign currencies.
2. Underwriting of equity, preference and debenture issues.
3. Subscribing to equity, preference and debenture issues.
4. Guaranteeing the deferred payments in respect of machinery imported from abroad or purchased in India; and
5. Guaranteeing of loans raised in foreign currency from foreign financial institutions.

Question 33.
Distinguish between money market and capital market?
Answer:
Money Market:

1. Money market is the mechanism through which short term funds are loaned and. borrowed. It designates financial institutions which handle the purchase, sale and transfer of short term credit instruments.
2. Commercial banks, acceptance houses, Non Banking Financial Institutions and the Central Bank are the institutions catering to the requirements of short term funds in the money Market.

Capital Market:

1. Capital Market is a part of financial system which is concerned with raising capital by dealing in shares, bonds and other long term investments.
2. The market where investment instruments like bonds, equities and mortgages are traded is known as the capital market.

Question 33.
Mention the objectives of demonetizations?
Answer:
Objectives of Demonetisation:

1. Removing Black Money from the country.
2. Stopping of Corruption.
3. Stopping Terror Funds.
4. Curbing Fake Notes.

Demonitisation is the act of stripping a currency unit of its status as legal tender. It occurs whenever there is a change of national currency. The current form or forms of money is pulled from circulation, often to bereplaced with new coins or notes.

Part – D
Answer The Following Questions In About A Page.

Question 34.
Explain the role of Commercial Banks in economic development?
Answer:
Role of Commercial Banks in Economic Development of a Country Role of Commercial Banks:

1. Capital Formation
2. Creation of Credit
3. Channelizing the funds
4. Encouraging Rights Type of Industries
5. Banks Monetize Debt
6. Finance to Government
7. Employment Generation
8. Bank Promote Entrepreneurship

1. Capital Formation:

1. Banks play an important role in capital formation, which is essential for the economic development of a country.
2. They mobilize the small savings of the people scattered over a wide area through their network of branches all over the country and make it available for productive purposes.

2. Creation of Credit:

1. Banks create credit for the purpose of providing more funds for development projects.
2. Credit creation leads to increased production, employment, sales and prices and thereby they bring about faster economic development.

3. Channelizing the Funds towards Productive Investment:

1. Banks invest the savings mobilized by them for productive purposes.
2. Capital formation is not the only function of commercial banks.

4. Encouraging Right Type of Industries:

1. Many banks help in the development of the right type of industries by extending loan to right type of persons.
2. In this way, they help not only for industrialization of the country but also for the economic development of the country.
3. They grant loans and advances to manufacturers whose products are in great demand.

5. Banks Monetize Debt:

1. Commercial banks transform the loan to be repaid after a certain period into cash, which can be immediately used for business activities.
2. Manufacturers and wholesale traders cannot increase their sales without selling goods on credit basis.

6. Finance to Government:

1. Government is acting as the promoter of industries in underdeveloped countries for which finance is needed for it.
2. Banks provide long – term credit to Government by investing their funds in Government securities and short-term finance by purchasing Treasury Bills.

7. Employment Generation:

1. After the nationalization of big banks, banking industry has grown to a great extent.
2. Bank’s branches are opened frequently, which leads to the creation of new employment opportunities.

8. Banks Promote Entrepreneurship:

• In recent days, banks have assumed the role of developing entrepreneurship particularly in developing countries like India by inducing new entrepreneurs to take up the well- formulated projects and provision of counseling services like technical and managerial guidance.

Question 36.
Elucidate the functions of Commercial Banks?
Answer:
The functions of commercial banks are broadly classified into primary functions and secondary functions.


Functions of Commercial Banks

(a) Primary Functions:
1. Accepting Deposits:
It implies that commercial banks are mainly dependent on public deposits.
There are two types of deposits

(I) Demand Deposits:
It refers to deposits that can be withdrawn by individuals without any prior notice to the bank. In other words, the owners of these deposits are allowed to withdraw money anytime by writing a withdrawal slip or a cheque at the bank counter or from ATM centres using debit card.

(II) Time Deposits:
It refers to deposits that are made for certain committed period of time. Banks pay higher interest on time deposits. These deposits can be withdrawn only after a specific time period by providing a written notice to the?bank.

2. Advancing Loans:

(a) It refers to granting loans to individuals and businesses. Commercial banks grant loans in the form of overdraft, cash credit, and discounting bills of exchange.

(b) Secondary Functions:
The secondary functions can be classified under three heads, namely, agency functions, general utility functions, and other functions.

1. Agency Functions:
It implies that commercial banks act as agents of customers by performing various functions.

(I) Collecting Cheques:
Banks collect cheques and bills of exchange on the behalf of their customers through clearing house facilities provided by the central bank.

(II) Collecting Income:
Commercial banks collect dividends, pension, salaries, rents, and interests on investments on behalf of their customers. A credit voucher is sent to customers for information when any income is collected by the bank.

(III) Paying Expenses:
Commercial banks make the payments of various obligations of customers, such as telephone bills, insurance premium, school fees, and rents.

2. General Utility Functions:
It implies that commercial banks provide some utility services to customers by performing various functions.

(I) Providing Locker Facilities:
Commercial banks provide locker facilities to its customers for safe custody of jewellery, shares, debentures, and other valuable items. This minimizes the risk of loss due to theft at homes. Banks are not responsible for the items in the lockers.

(II) Issuing Traveler’s Cheques:
Banks issue traveler’s cheques to individuals for traveling outside the country. Traveler’s cheques are the safe and easy way to protect money while traveling.

(III) Dealing in Foreign Exchange:
Commercial banks help in providing foreign exchange to businessmen dealing in exports and imports. However, commercial banks need to take the permission of the Central Bank for dealing in foreign exchange.

3. Transferring Funds:
It refers to transferring of funds from one bank to another. Funds are transferred by means of draft, telephonic transfer, and electronic transfer.

4. Letter of Credit:
Commercial banks issue letters of credit to their customers to certify their creditworthiness.

(I) Underwriting Securities:
Commercial banks also undertake the task of underwriting securities. As public has full faith in the credit worthiness of banks, public do not hesitate in buying the securities underwritten by banks.

(II) Electronic Banking:
It includes services, such as debit cards, credit cards, and Internet banking.

(c) Other Functions:

(I) Money Supply:
It refers to one of the important functions of commercial banks that help in increasing money supply.

(II) Credit Creation:
Credit Creation means the multiplication of loans and advances. Commercial banks receive deposits from the public and use these deposits to give loans.

Question 37.
Describe the functions of Reserve Bank of India?
Answer:
Functions of Central Bank (Reserve Bank of India):
The Reserve Bank of India (RBI) is India’s central banking institution, which controls the monetary policy of the Indian rupee.

1. Monetary Authority:
It controls the supply of money in the economy to stabilize exchange rate, maintain healthy balance of payment, attain financial stability, control inflation, strengthen banking system.

2. The issuer of currency:
The objective is to maintain the currency and credit system of the country. It is the sole authority to issue currency. It also takes action to control the circulation of fake currency.

3. The issuer of Banking License:
As per Sec 22 of Banking Regulation Act, every bank has to obtain a banking license from RBI to conduct banking business in India.

4. Banker to the Government:
It acts as banker both to the central and the state governments. It provides short-term credit. It manages all new issues of government loans, servicing the government debt outstanding and nurturing the market for government securities. It advises the government on banking and financial subjects.

5. Banker’s Bank:
RBI is the bank of all banks in India as it provides loan to banks, accept the deposit of banks, and rediscount the bills of banks.

6. Lender of last resort:
The banks can borrow from the RBI by keeping eligible securities as collateral at the time of need or crisis, when there is no other source.

7. Act as clearing house:
For settlement of banking transactions, RBI manages 14 clearing houses. It facilitates the exchange of instruments and processing of payment instructions.

8. Custodian of foreign exchange reserves:
It acts as a custodian of FOREX. It administers and enforces the provision of Foreign Exchange Management Act (FEMA), 1999. RBI buys and sells foreign currency to maintain the exchange rate of Indian rupee v/s foreign currencies.

9. Regulator of Economy:
It controls the money supply in the system, monitors different key indicators like GDP, Inflation, etc.

10. Managing Government securities:
RBI administers investments in institutions when they invest specified minimum proportions of their total assets/liabilities in government securities.

11. Regulator and Supervisor of Payment and Settlement Systems:
The Payment and Settlement Systems Act of 2007 (PSS Act) gives RBI oversight authority for the payment and settlement systems in the country. RBI focuses on the development and functioning of safe, secure and efficient payment and settlement mechanisms.

12. Developmental Role:
This role includes the development of the quality banking system in India and ensuring that credit is available to the productive sectors of the economy. It provides a wide range of promotional functions to support national objectives.

It also includes establishing institutions designed to build the country’s financial infrastructure. It also helps in expanding access to affordable financial services and promoting financial education and literacy.

13. Publisher of monetary data and other data:
RBI maintains and provides all essential banking and other economic data, formulating and critically evaluating the economic policies in India. RBI collects, collates and publishes data regularly.

14. Exchange manager and controller:
RBI represents India as a member of the International Monetary Fund [IMF], Most of the commercial banks are authorized dealers of RBI.

15. Banking Ombudsman Scheme:
RBI introduced the Banking Ombudsman Scheme in 1995. Under this scheme, the complainants can file their complaints in any form, including online and can also appeal to the Ombudsman against the awards and the other decisions of the Banks.

16. Banking Codes and Standards Board of India:
To measure the performance of banks against Codes and standards based on established global practices, the RBI has set up the Banking Codes and Standards Board of India (BCSBI).

Question 38.
What are the objectives of Monetary Policy? Explain?
The specific objectives of monetary policy are Objectives of monetary policy:

1. Neutrality of Money
2. Stability of Exchange Rates
3. Price Stability
4. Full Employment
5. Economic Growth
6. Equilibrium in the Balance of Payments

1. Neutrality of Money:

1. Economists like Wicksteed, Hayek and Robertson are the chief exponents of neutral money.
2. They hold the view that monetary authority should aim at neutrality of money in the economy.
3. Monetary changes could be the root cause of all economic fluctuations.
4. According to neutralists, the monetary change causes distortion and disturbances in the proper operation of the economic system of the country.

2. Exchange Rate Stability:

1. Exchange rate stability was the traditional objective of monetary authority.
2. This was the main objective under Gold Standard among different countries.
3. When there was disequilibrium in the balance of payments of the country, it was automatically corrected by movements.

3. Price Stability:

1. Economists like Crustave Cassel and Keynes suggested price stabilization as a main objective of monetary policy.
2. Price stability is considered the most genuine objective of monetary policy.
3. Stable prices repose public confidence.
4. It promotes business activity and ensures equitable distribution of income and wealth.

4. Full Employment:

1. During world depression, the problem of unemployment had increased rapidly.
2. It was regarded as socially dangerous, economically wasteful and morally deplorable.
3. Thus, full employment was considered as the main goal of monetary policy.

5. Economic Growth:

1. Economic growth is the process whereby the real per capita income of a country increases over a long period of time.
2. It implies an increase in the total physical or real output, production of goods for the satisfaction of human wants.
3. Monetary policy should promote sustained and continuous economic growth by maintaining equilibrium between the total demand for money and total production capacity and further creating favourable conditions for saving and investment.

6. Equilibrium in the Balance of Payments:

• Equilibrium in the balance of payments is another objective of monetary policy which emerged significant in the post war years.

Samacheer Kalvi 12th Economics Banking Additional Questions and Answers

Part – A
I. Multiple Choice Questions.

Question 1.
Reserve Bank of India was nationalised in …………………………
(a) 1947
(b) 1948
(c) 1949
(d)1950
Answer:
(c) 1949

Question 2.
Overdraft is a facility offered by commercial banks to …………………………
(a) Exporters
(b) Importers
(c) Farmers
(d) Businessmen
Answer:
(d) Businessmen

Question 3.
Current account deposites are operated by …………………………
(a) Agriculturists
(b) Business mens
(c) Goverment servants
(d) Labourers
Answer:
(b) Business mens

Question 4.
Primary functions of the commercial bank is …………………………
(a) Accepting deposits from the public
(b) Making loans and advances to public
(c) Discounting bills of exchange
(d) Inter bank borrowing
Answer:
(a) Accepting deposits from the public

Question 5.
The first bank in India was established in …………………………
(a) 1670
(b) 1770
(c) 1870
(d) 1872
Answer:
(b) 1770

Question 6.
The coins are issued by …………………………
(a) Ministry of Finance
(b) RBI
(c) Central Bank
(d) State Bank
Answer:
(a) Ministry of Finance

Question 7.
The amount of cash kept by commercial banks to meet the day to day transactions is known as …………………………
(a) Bank cash
(b) Commercial bank cash
(c) Reserve cash
(d) Cheque
Answer:
(c) Reserve cash

Question 8.
In India, Central bank is known as –
(a) SBI
(b) RBI
(c) Commercial bank
(d) IDBI
Answer:
(b) RBI

Question 9.
Open Market operations enable the ………………………… to reduce the money supply in the economy.
(o) Commercial bank
(b) SBI
(c) ICICI
(d) RBI
Answer:
(d) RBI

Question 10.
………………………… Bank Finance the Import and Export trade.
(a) Industrial Bank
(b) Exim Bank
(c) Co – operative Bank
(d) RBI
Answer:
(b) Exim Bank

Question 11.
Commercial Banks create credit in favour of the …………………………
(a) Consumers
(b) Business men
(c) Customers
(d) Agriculturists
Answer:
(c) Customers

Question 12.
………………………… is a non profit making financial institution of the country.
(a) Central Bank
(b) Commercial Bank
(c) Co – operative Bank
(d) Industrial Bank
Answer:

Question 13.
Extending banking facilities to the rural and semi urban areas is the promotional activity of the …………………………
(a) Co – operative Bank
(b) Commercial Bank
(c) RBI
(d) State Bank
Answer:
(a) Co – operative Bank

Question 14.
The qualitative credit control methods are also called …………………………
(a) Selective cash control
(b) Selective expenditure control
(c) Selective credit control
(d) Selective money control
Answer:
(c) Selective credit control

Question 15.
Withdraw money more than deposit is called …………………………
(a) Cash credit
(b) Discounting bill
(c) Current account
(d) Over draft
Answer:
(d) Over draft

Question 16.
………………………… help in proper allocation of funds among different regions of the economy.
(a) Central banks
(b) Co – operative banks
(c) Commercial banks
(d) Agriculture banks
Answer:
(c) Commercial banks

Question 17.
Lowering the Bank rate off sets ……………………….. tendencies.
(a) Deflationary
(b) Inflationary
(c) Stagflationary
(d) Hyper inflationary
Answer:
(a) Deflationary

Question 18.
The main aim of the Central bank is …………………………
(a) Full employment
(b) Economic stability
(c) Balance of payment
(d) International capital movement
Answer:
(b) Economic stability

Question 19.
………………………… Bank regulates the credit and currency according to the economic situation of the country.
(a) State
(b) Commercial
(c) RBI
(d) Agriculture
Answer:
(b) Economic stability

Question 20.
………………………… credit control method mean the Regulation and control of the supply of the credit among its possible users.
(a) Quantitative
(b) Qualitative
(c) General
(d) Possible
Answer:
(b) Qualitative

Question 21.
The issue of paper money is the most important function of a …………………………
(a) Commercial Bank
(b) Central Bank
(c) ICICI Bank
(d) State Bank
Answer:
(b) Central Bank

Question 22.
………………………… stimulate saving and investment.
(a) Credit
(b) Bank
(c) Debit
(d) Cheque
Answer:
(b) Bank

Question 23.
The commercial banks only deal in foreign exchange under the directions of the …………………………
(a) State bank
(b) Central bank
(c) Commercial bank
(d) Co – operative bank
Answer:
(b) Central bank

Question 24.
Fixed Deposits are otherwise known as …………………………
(a) Bank Deposits
(b) Customer’s Deposits
(c) Time Deposits
(d) Money Deposits
Answer:
(c) Time Deposits

Question 25.
The rate of interest of every Central bank is known as …………………………
(a) Interest rate
(b) Credit rate
(c) Debit rate
(d) Bank rate
Answer:
(d) Bank rate

II. Match the following and choose the correct answer by using codes given below.

Question 1.
A. Saving Deposits – (i) Official minimum rate
B. Cash credit – (ii) Cheque facilities
C. Bank rate – (iii) Facility to business man
D. Over draft – (iv) Collateral security
Codes:
(a) A (ii) B (iv) C (i) D (iii)
(b) A (i) B (ii) C (iii) D (iv)
(c) A (iii) B (i) C (iv) D (ii)
(d) A (iv) B (iii) C (ii) D (i)
Answer:
(a) A (ii) B (iv) C (i) D (iii)

Question 2.
A. Transfer of funds – (i) Buying and selling
B. Commercial bank – (ii) Clearing
C. Open market operation – (iii) Interest not given
D. Demand deposits – (iv) Profit making
Codes:
(a) A (ii) B (iv) C (i) D (iii)
(b) A (i) B (iii) C (ii) D (iv)
(c) A (iii) B (ii) C (iv) D (i)
(d) A (iv) B (i) C (iii) D (ii)
Answer:
(a) A (ii) B (iv) C (i) D (iii)

Question 3.
A. NBFI – (i) Monetary policy
B. Per Capita Income – (ii) Minimum amount of fund
C. Inflation – (iii) Economic growth
D. RTGS – (iv) Non – bank Financial Institution
Codes:
(a) A (iii) B (ii) C (iv) D (i)
(b) A (iv) B (iii) C (i) D (ii)
(c) A (ii) B (i) C (iii) D (iv)
(d) A (i) B (iv) C (ii) D (iii)
Answer:
(b) A (iv) B (iii) C (i) D (ii)

Question 4.
A. UTI – (i) Quantitative credit control
B. Open market operation – (ii) Mutual fund
C. Bank – (iii) Automatic Teller mechine
D. ATM – (iv) Financial Institution
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (iv) C (ii) D (i)
(c) A (iv) B (iii) C (i) D (ii)
(d) A (ii) B (i) C (iv) D (iii)
Answer:
(d) A (ii) B (i) C (iv) D (iii)

Question 5.
A. NABARD – (i) Internet banking
B. SFC – (ii) Short term seasonal credit
C. Rationing of credit – (iii) State level institution
D. Online banking – (iv) Qualitative credit control of RBI
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (iv) C (i) D (ii)
(c) A (ii) B (iii) C (iv) D (i)
(d) A (iv) B (i) C (ii) D (iii)
Answer:
(c) A (ii) B (iii) C (iv) D (i)

III. State whether the statements are true or false.

Question 1.
(i) Business men operates the current account deposits.
(ii) State Bank organization established EXIM Bank

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 2.
(i) The Central bank of a country acts as the banker, fiscal agent and advisor to the government.
(ii) The banks expand their loans resulting in the expansion of investment employment production and prices.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 3.
(i) NABARD provides agriculture finance to medium and long term basis.
(ii) Bank observed that credit is the lubricant of all commerce and trade.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 4.
(i) State Bank is the financial advisor to the government.
(ii) Central Bank possesses the monopoly of note issue.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(d) (i) is false but (ii) is true

Question 5.
(i) For maintaining saving deposits, cheque facilities can be enjoyed.
(ii) Fixed Deposits are otherwise known as time deposits.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

IV. Which of the following is correctly matched.

Question 1.
(a) EXIM Bank – Export and Import
(b) NABARD – Industrial finance
(c) Bank – Excess money
(d) Fixed Deposits – Bank saving
Answer:
(a) EXIM Bank – Export and Import

Question 2.
(a) CRR – Current Reserve Ratio
(b) Saving deposits – Cheque facilities
(c) Bank rate policy – High interest
(d) Adviser to government – SBI
Answer:
(b) Saving deposits – Cheque facilities

Question 3.
(a) ICICI Bank – Three tier Export Bank
(b) NABARD – Agriculture Finance
(c) IDBI – Co – operative Bank
(d) IFCI – State Bank
Answer:
(b) NABARD – Agriculture Finance

Question 4.
(a) South African Reserve Bank – 1921
(b) The Central bank of China – 1934
(c) The Reserve Bank of Newzealand – 1928
(d) The Reserve Bank of India – 1935
Answer:
(d) The Reserve Bank of India – 1935

Question 5.
(a) Forex cards – Smart card
(b) Paper currency – Legal tender
(c) Medium of Exchange – Functions of money
(d) CRR – Credit Reserve Ratio
Answer:
(c) Medium of Exchange – Functions of money

V. Which of the following is not correctly matched.

Question 1.
(a) RBI – Reserv e Bank of India
(b) SBI – State Bank of India
(c) IMF – International Monetary Fund
(d) ATM – Any Time Money
Answer:
(d) ATM – Any Time Money

Question 2.
(a) Qualitative credit control of RBI – Rationing of credit
(b) Agricultural credit department – To finance the rural sector
(c) NABARD – Short term seasonal credit
(d) UTI – Mutual fund
Answer:
(d) UTI – Mutual fund

Question 3.
(a) RBI – Central Bank of SBI
(b) ARDC – The agricultural refinance development corporation
(c) Bank Crdit – Bank loans and advances
(d) Moral suasion – Persuasion
Answer:
(a) RBI – Central Bank of SBI

Question 4.
(a) Traveler’s cheques – Group of people
(b) Credit creation – Multiplication of loans and advances
(c) Primary deposits – Passive deposits
(d) Bank – Financial Institution
Answer:
(a) Traveler’s cheques – Group of people

Question 5.
(a) RBI – Monetary authority
(b) Bank rate – Re – discounting
(c) Recession – Monetary policy
(d) Keynes – Economic growth
Answer:
(d) Keynes – Economic growth

Question 6.
(a) RTGS – Real Time Gross Settlement
(b) NEFT – National Electronic Fund Transfer
(c) ATM – Any Time Money
(d) SIDCO – Small Industrial Development Corporation
Answer:
(c) ATM – Any Time Money

VI. Pick the odd one out.

Question 1.
1. Commercial Bank Secondary Functions
(a) Agency functions
(b) General utility services
(c) Transfer of bank
(d) Credit creation
Answer:
(c) Transfer of bank

Question 2.
Functions of Central Bank
(a) Monetary Authority
(b) The issuer of currency
(c) Banker to the foreign level
(d) Banker’s Bank
Answer:
(c) Banker to the foreign level

Question 3.
The frequent methods of credit control under Selective method is called ……………………..
(a) Rationing of credit
(b) Direct Action of Industries
(c) Method of publicity
(d) Moral persuasion
Answer:
(b) Direct Action of Industries

Question 4.
Functions of ICICI is called ……………………..
(a) Assistance to Industries
(b) Merchant banking
(c) Credit bank operation
(d) Project promotion
Answer:
(c) Credit bank operation

Question 5.
The main objectives of Demonetisation ……………………..
(a) Removing black money from the country
(b) Stopping of corruption
(c) Stopping Terror Funds
(d) Fake notes given
Answer:
(d) Fake notes given

VII. Assertion and Reason.

Question 1.
Assertion (A): Commercial banks provide some utility services to the customers.
Reason (R): Credit creation leads to increased production, employment, sales and prices.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 2.
Assertion (A): Bank rate means re – discounting the first class securities.
Reason (R): Credit creation means not given loans and advances.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 3.
Assertion (A): Bank is service institution.
Reason (R): Commercial Bank is an institutions that provides accepting deposits and providing loans to the public.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Question 4.
Assertion (A): Credit creation leads to increase in production.
Reason (R): Credit creation means the multiplication of loans and advances.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 5.
Assertion (A): The objectives of demonetization is called issuing currency notes.
Reason (R): Black money accepted.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 6.
Assertion (A): Primary deposits are also called as passive deposits.
Reason (R): Passive deposits are also called as time deposits.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Part – B
Answer The Following Questions In One or Two Sentences.

Question 1.
What is meaning of primary deposite and derived deposit?
Answer:

1. The modem banks create deposits in two ways. They are primary deposit and derived deposit.
2. When a customer gives cash to the bank and the bank creates a book debt in his name called a deposit, it is known as a “primary deposit”.
3. But when such a deposit is created, without there being any prior payment of equivalent cash to the bank, it is called a ‘derived deposit’.

Question 2.
What are the functions of primary deposits?
Answer:
Primary Deposits:

1. It is out of these primary deposits that the bank makes loans and advances to its customers.
2. The initiative is taken by the customers themselves. In this case, the role of the bank is passive.
3. So these deposits are also called “Passive deposits”.

Question 3.
What are the credit control measures?
Answer:

Question 4.
Define RBI Rural credit?
Answer:
Reserve Bank of India and Rural Credit:
In a developing econorqy like India, the Central bank of the country cannot confine itself to the monetary regulation only, and it is expected that it should take part in development function in all sectors especially in the agriculture and industry.

Question 5.
Write RBI granting Regional Rural Banks concessions?
Answer:
The RBI has been granting many concessions to RRBs:

1. 1. They are allowed to maintain cash reserve ratio at 3 per cent and statutory liquidity ratio at 25 per cent; and
   2. They also provide refinance facilities through NABARD.

Question 6.
Define Three Tier co – operative credit structure?
Answer:

Part – C
Answer The Following Questions In One Paragraph.

Question 1.
What are the functions of RBI agricultural credit?
Answer:
Role of RBI in agricultural credit:

1. RBI has been playing a very vital role in the provision of agricultural finance in the country.
2. The Bank’s responsibility in this field had been increased due to the predominance of agriculture in the Indian economy and the inadequacy of the formal agencies to cater to the huge requirements of the sector.
3. In order to fulfill this important role effectively, the RBI set up a separate Agriculture Credit Department.
4. However, the volume of informal loans has not declined sufficiently.

Question 2.
What are the ARDC – objectives?
Answer:
Objectives of the ARDC:

1. To provide necessary funds by way of refinance to eligible institutions such as the Central Land Development Banks, State Co – operative Banks, and Scheduled banks.
2. To subscribe to the debentures floated by the Central Land Development banks, State Co-operative Banks, and Scheduled banks, provided they were approved by the RBI.

Question 3.
Describe the functions of IDBI?
Answer:
Functions of IDBI:

1. The functions of IDBI fall into two groups
   1. Assistance to other financial institutions; and –
   2. Direct assistance to industrial concerns either on its own or in participation with other institutions.
2. The IDBI can provide refinance in respect of term loans to industrial concerns given by the IFC, the SFCs, other financial institutions notified by the Government, scheduled banks and state cooperative banks.
3. A special feature of the IDBI is the provision for the creation of a special fund known as the Development Assistance Fund.
4. The fund is intended to provide assistance to industries which require heavy investments with low anticipated rate of return.
5. Such industries may not be able to get assistance in the normal course.
6. The financing of exports was also undertaken by the IDBI till the establishment of EXIM BANK in March, 1982.

Question 4.
Difference between NEFT and RTGS?
Answer:
NEFT:

1. National electronic Fund Transfer
2. Transactions happens in batches hence slow
3. Timings: 8:00 am to 6:30 pm (12:30 pm on Saturday)
4. No minimum limit

RTGS:

1. Real Time Gross Settlement
2. Transactions happens in real time hence fast
3. Timings : 9:00 am to 4:30 pm (1:30 pm on Saturday)
4. Minimum amount for RTGS transfer is ₹ 2 lakhs

Question 5.
What is E – Banking?
Answer:

1. Online banking, also known as internet banking, is an electronic payment system that enables customers of a bank or other financial institution to conduct a range of financial transactions through the financial institution’s website.
2. The online banking system typically connects to or be part of the core banking system operated by a bank and is in contrast to branch banking which was the traditional way customers accessed banking services.

Part – D
Answer The Following Questions In One Page.

Question 1.
Describe the frequent methods of selective method credit control?
Answer:
Qualitative or Selective Method of Credit Control:

1. The qualitative or the selective methods are directed towards the diversion of credit into particular uses or channels in the economy.
2. Their objective is mainly to control and regulate the flow of credit into particular industries or businesses.
3. The following are the frequent methods of credit control under selective method:
4. Rationing of Credit:
   1. Direct Action
   2. Moral Persuasion
   3. Method of Publicity
   4. Regulation of Consumer’s Credit
   5. Regulating the Marginal Requirements on Security Loans
   6. Rationing of Credit:

1. Rationing of Credit:

• This is the oldest method of credit control.
• Rationing of credit as an instrument of credit control was first used by the Bank of England by the end of the 18th Century.
• It aims to control and regulate the purposes for which credit is granted by commercial banks. It is generally of two types.

(I) The variable portfolio ceiling:
It refers to the system by which the central bank fixes ceiling or maximum amount of loans and advances for every commercial bank.

(II) The variable capital asset ratio:
It refers to the system by which the central bank fixes the ratio which the capital of the commercial bank should have to the total assets of the bank.

2. Direct Action:
Direct action against the erring banks can take the following forms.

• The central bank may refuse to altogether grant discounting facilities to such banks.
• The central bank may refuse to sanction further financial accommodation to a bank whose existing borrowing are found to be in excess of its capital and reserves.
• The central bank may start charging penal rate of interest on money borrowed by a bank beyond the prescribed limit.

3. Moral Suasion:

• This method is frequently adopted by the Central Bank to exercise control over the Commercial Banks.
• Under this method Central Bank gives advice, then requests and persuades the Commercial Banks to co-operate with the Central Bank in implementing its credit policies.

4. Publicity:

• Central Bank in order to make their policies successful, take the course of the medium of publicity.
• A policy can be effectively successful only when an effective public opinion is created in its favour.

5. Regulation of Consumer’s Credit:

• The down payment is raised and the number of installments reduced for the credit sale, (vz) Changes in the Marginal Requirements on Security Loans:
• This system is mostly followed in U.S.A.
• Under this system, the Board of Governors of the Federal Reserve System has been given the power to prescribe margin requirements for the purpose of preventing an excessive use of credit for stock exchange speculation.

Question 2.
Describe the Merger of Banks?
Answer:
Merger of Banks:

1. Union Cabinet decided to merge all the remaining five associate banks of State Bank Group with State Bank of India in 2017.

2. After the Parliament passed the merger Bill, the subsidiary banks have ceased to exist.

3. Five associates and the Bharatiya Mahila Bank have become the part of State Bank of India (SBI) beginning April 1, 2017.

4. This has placed State Bank of India among the top 50 banks in the world.

5. The five associate banks that were merged are State Bank of Bikaner and Jaipur (SBBJ), State Bank of Hyderabad (SBH), State Bank of Mysore (SBM), State Bank of Patiala (SBP) and State Bank of Travancore (SBT).

6. The other two Associate Banks namely State Bank of Indore and State Bank of Saurashtra had already been merged with State Bank of India.

7. After the merger, the total customer base of SBI increased to 37 crore with a branch network of around 24,000 and around 60,000 ATMs across the country.

Question 3.
Briefly describe the ATM?
Answer:
ATM (Automated Teller Machine):

1. ATMs transformed the bank tech system when they were first introduced in 1967.
2. The next revolution in ATMs is likely to involve contactless payments.
3. Much like Apple Pay or Google Wallet, soon we will be able to conduct contactless ATM transactions using a smartphone.
4. Some ATM innovations are already available overseas.
5. For example, biometric authentication is already used in India, and its recognition is in place at Qatar National Bank ATMs.
6. These technologies can help overall bank security by protecting against ATM hacks.

Question 4.
Explain the State Industrial Development Corporations?
Answer:
State Industrial Development Corporations (SIDCOs):

• The Industrial Development Corporations have been set up by the state governments and they are wholly owned by them.
• These institutions are not merely financing agencies; they are entrusted with the responsibility of accelerating the industrialization of their states.

SIDCO (Small Industrial Development Corporation):

• SIDCOs provide financial assistance to industrial concerns by way of loans guarantees and underwriting of or direct subscriptions to shares and debentures.
• In addition to these, they undertake various promotional activities, such as conducting techno-economic surveys, project identification, preparation of feasibility studies and selection and training of entrepreneurs.
• They also promote joint sector projects in association with private promoter in such type of projects.
• SIDCOs take 26 percent, private co-promoter takes 25 percent of the equity, and the rest is offered to the investing public.
• SIDCOs undertake the development of industrial areas by providing all infrastructural facilities and initiation of new growth centers.
• They also administer various State government incentive schemes.
• SIDCOs get refinance facilities form IDBI.
• They also borrow through bonds and accept deposits.