Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.2

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.2

Question 1.
If ^{(n – 1)} P₃ : ⁿP₄, find n:
Solution:

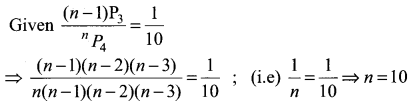
Question 2.
If ¹⁰P_{r – 1} = 2 × ⁶P_r, find r.
Solution:

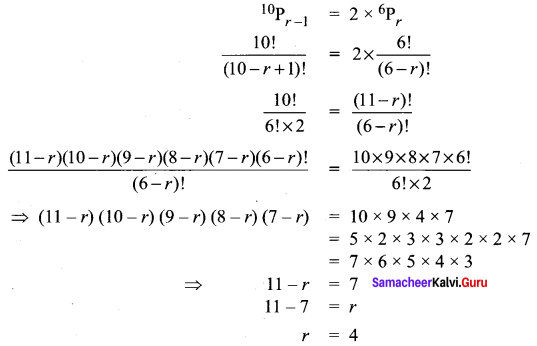
Question 3.
(i) Suppose 8 people enter an event in a swimming meet. In how many ways could the gold, silver, and bronze prizes be awarded?
Solution:
Number people enter in a swimming meet = 8 Prizes awarded = Gold, silver, bronze.
The gold medal can be awarded to any one of the 8 people in 8 ways. The silver medal can be awarded to any one of the remaining 7 people in 7 ways. The bronze medal can be awarded to any one of the remaining 6 people in 6 ways,
∴ Total number of ways of awarding the prizes = 8 × 7 × 6 = 336

(ii) Three men have 4 coats, 5 waistcoats, and 6 caps. In how many ways can they wear them?
Solution:
Selecting and arranging 3 coats from 4 can be done in ⁴P₃ ways
Selecting and arranging 3 waistcoats from 5 can be done in ⁵P₃ ways Selecting and arranging 3 caps from 6 can be done in ⁶P₃ ways
∴ Total number of ways = ⁴P₃ × ⁵P₃ × ⁶P₃ = 172800 ways

Question 4.
Determine the number of permutations of the letters of the word SIMPLE if all are taken at a time?
Solution:
Number of letters in the word SIMPLE = 6
The total number of the word is equal to the number of arrangements of these letters, taken all at a time
∴ Total number of words = 6P₆ = 6!
= 6 × 5 × 4 × 3 × 2 × 1
= 720

Question 5.
A test consists of 10 multiple-choice questions. In how many ways can the test be answered if

(i) Each question has four choices?
Solution:
Total number of questions = 10
Each question has four choices.
Each question can be answered in 4 ways.
∴ The total number of ways of answering 10 questions
= 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4
= 4¹⁰

(ii) The first four questions have three choices and the remaining have five choices?
Solution:
The first four questions have three choices and the remaining have five choices
First, four questions have three choices.
∴ The number of ways of answering the first four questions is = 3 × 3 × 3 × 3 = 3⁴
The remaining six questions have 5 choices
∴ The number of ways of answering the remaining 6 questions is = 5 × 5 × 5 × 5 × 5 × 5 = 5⁶
∴ The total number of ways of answering the questions = 3⁴ × 5⁶

(iii) Question number n has n + 1 choices?
Solution:
Question number n has n + 1 choices.
The first question has a 1 + 1 choice.
∴ Number of ways of answering the first question = 2
The second question has 2 + 1 choices
∴ Number ways of answering second question = 3

Tenth question has (10 + 1) choices
∴ Number of ways of answering tenth question = 11
∴ A total number of ways of answering the given 10 questions = 2 × 3 × 4 × ……. × 11 = 11!

Question 6.
A student appears in an objective test which contain 5 multiple-choice questions. Each question has four choices out of which one correct answer.

(i) What is the maximum number of different answers can the students give?
Solution:
Number multiple-choice questions = 5
Number of ways of answering each question = 4
∴ The total number of ways of answering the five questions = 4 × 4 × 4 × 4 × 4 = 45
Hence, the maximum number of different answers = 4⁵

(ii) How will the answer change if each question may have more than one correct answers?
Solution:
When each question has more than 1 correct answer.
Selecting the correct choice from the 4 choice can be done is ⁴C₁ or ⁴C₂ or ⁴C₃ or ⁴C₄ ways.

Each question can be answered in 15 ways.
Number of questions = 5
∴ Total number of ways = 15⁵

Question 7.
How many strings can be formed from the letters of the word ARTICLE, so that vowels occupy the even places?
Solution:
The given word is ARTICLE
Number of letters in the word = 7
Vowels in the given word = A, I, E
Number of vowels in the given word = 3

∴ Number of even places = 3
3 Vowels can occupy the 3 even places in 3P3 = 3! ways
The remaining 4 letters can occupy the remaining places in
4P₄ = 4! ways
Hence a total number of ways of arrangement = 4! × 3! = 4 × 3 × 2 × 3 × 2 = 144

Question 8.
8 women and 6 men are standing in a line.
(i) How many arrangements are possible if any individual can stand in any position?
Solution:
Total number of persons in a line = 8 + 6 = 14
The number of ways of standing 14 persons in a line in any position = 14P₁₄ = 14!

(ii) In how many arrangements will all 6 men be standing next to one another?
Solution:
Consider 6 men as one unit.
8 women + 6 men as one unit = 9 can be arranged in 9! ways.
6 men can among themselves be arranged in 6! ways.
∴ A total number of ways of arrangement = 9! × 6!

(iii) In how many arrangements will no two men be standing next to one another?
Solution:
Since no two men be together they have to be placed between 8 women and before and after the women.
w | w | w | w | w | w | w | w
There are 9 places so the 6 men can be arranged in the 9 places in ⁹P₆ ways.
After this arrangement, the 8 women can be arranged in 8! ways.
∴ Total number of arrangements = (⁹P₆) × 8!

Question 9.
Find the distinct permutations of the letters of the word MISSISSIPPI?
Solution:
MISSISSIPPI
Number of letters = 11
Here M – 1 time
I – 4 times
S – 4 times
P – 2 times

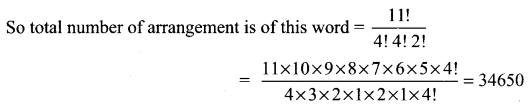
Question 10.
How many ways can the product a2b3c4 be expressed without exponents?
Solution:
a²b³c⁴ = aabbbcccc
Number of letters = 9
a = 2 times,
b = 3 times,
c = 4 times,

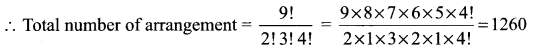
Question 11.
In how many ways 4 mathematics books, 3 physics books, 2 chemistry books and 1 biology book can be arranged on a shelf so that all books of the same subjects are together.
Solution:
Number of subjects = 4
4 subjects can be arranged in the shelf in 4! ways Number of mathematics books = 4
4 Mathematics books keeping together can be arranged in 4! ways
Number of physics books = 3
3 Physics books keeping together can be arranged in 3! ways.
Number of chemistry books =2
2 Chemistry books keeping together can be arranged in 2! ways.
Number of biology books = 1
1 biology book can be arranged in 1! way
Hence, the total numbers of ways of arranging the books
= 4! × 4! × 3! × 2! × 1!
= (4 × 3 × 2 × 1) (4 × 3 × 2 × 1) × (3 × 2) (2 × 1)
= 24 × 24 × 6 × 2
= 6912

Question 12.
In how many ways can the letters of the word SUCCESS be arranged so that all Ss are together?
Solution:
The given word is SUCCESS
Number of letters other than S = 4
Treating all S’s together as one letter
Total number of letters in the word = 5
Number of U’s = 1
Number of C’s = 2
Number of E’s = 1
Number of S’s (treated as one letter ) = 1
Number of ways of arranging = \(\frac{5 !}{2 ! \times 1 ! \times 1 ! \times 1 !}\)
= \(\frac{5 \times 4 \times 3 \times 2 \times 1}{2 \times 1}\)
= 5 × 4 × 3
= 60 ways

Question 13.
A coin is tossed 8 times,

(i) How many different sequences of heads and tails are possible?
Solution:
Number of coins tossed = 8
Number of outcome for each toss = 2
Total number of outcomes = 28

(ii) How many different sequences containing six heads and two tails are possible?
Solution:
Getting 6 heads and 2 tails can be done in ⁸P₆ or ⁸P₂ ways

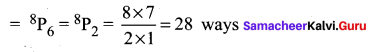
Question 14.
How many strings are there using the letters of the word INTERMEDIATE, if

(i) The vowels and consonants are alternative
Solution:
INTERMEDIATE

The number of ways in which vowels and consonants are alternative = \(\frac{6 ! 6 !}{3 ! 2 !}=\) 43200

(ii) All the vowels are together
Solution:
The number of arrangements:
Keeping all the vowels as a single unit. Now we have 6 + 1 = 7 units which can be arranged in 7! ways.
Now the 6 consonants can be arranged in \(\frac{6 !}{2 !}\) (T occurs twice) ways in vowels, I – repeats thrice
and E – repeats twice

(iii) Vowels are never together (and) (iv) No two vowels are together.
Solution:
Vowels should not be together = No. of all arrangements – No. of all vowels together

So number of ways in which No two vowels are together = 19958400 – Number of ways in which vowels are together = 19958400 – 151200 = 19807200

Question 15.
Each of the digits 1,1, 2, 3, 3 and 4 is written on a separate card. The seven cards are then laid out in a row to form a 6-digit number.

(i) How many distinct 6-digit numbers are there?
Solution:
The given digits are 1, 1, 2, 3, 3, 4
The 6 digits can be arranged in 6! ways
In which 1 and 3 are repeated twice.

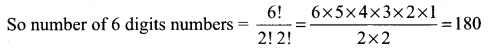
(ii) How many of these 6-digit numbers are even?
Solution:
To find the number even numbers
The digit in unit place is 2 or 4 which can be filled in 2 ways

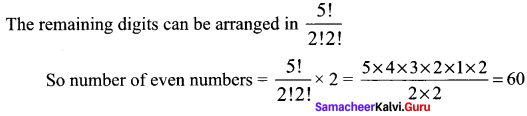
(iii) How many of these 6-digit numbers are divisible by 4?
Solution:
To get a number -f- by 4 the last 2 digits should be -r- by 4 So the last two digits will be 12 or 24 or 32.
When the last 2 digits are 1 and 2.

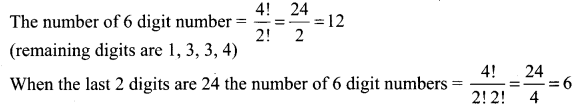
When the last 2 digits are 3 and the number of 6 digit numbers (remaining number 1, 1, 3, 4)
So there of 6 digit numbers ÷ by 4 = 12 + 6 + 12 = 30

Question 16.
If the letters of the word GARDEN are permuted in all possible ways and the strings thus formed are arranged in the dictionary order, then find the ranks of the words
(i) GARDEN
(ii) DANGER.
Solution:
The given letters are GARDEN.
To find the rank of GARDEN:
The given letters in alphabetical order are A D E G N R

The rank of GARDEN is 379
To find the rank of DANGER

(ii) The No. of words starting with A = 5! =120

Question 17.
Find the number of strings that can be made using all letters of the word THING. If these words are written as in a dictionary, what will be the 85^th string?
Solution:
(i) Number of words formed = 5! = 120
(ii) The given word is THING
Taking the letters in alphabetical order G H I N T
To find the 85^th word

Question 18.
If the letters of the word FUNNY are permuted in all possible ways and the strings thus formed are arranged in the dictionary order, find the rank of the word FUNNY.
Solution:
The given word is FUNNY

Question 19.
Find the sum of all 4-digit numbers that can be formed using digits 1, 2, 3, 4, and 5 repetitions not allowed?
Solution:
The given digits are 1, 2, 3, 4, 5
The no. of 4 digit numbers

Sum of the digits = 1 + 2 + 3 + 4 + 5 = 15
Sum of number’s in each place = 24 × 15 = 360

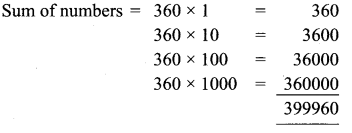
Question 20.
Find the sum of all 4-digit numbers that can be formed using digits 0, 2, 5, 7, 8 without repetition?
Solution:
The given digits are 0, 2, 5, 7, 8
To get the number of 4 digit numbers
1000’s place can be filled in 4 ways (excluding 0)
100’s place can be filled in 4 ways (excluding one number and including 0)
10’s place can be filled in (4 – 1) = 3 ways
and unit place can be filled in (3 – 1) = 2 ways
So the number of 4 digit numbers = 4 × 4 × 3 × 2 = 96

To find the sum of 96 numbers:

In 1000’s place we have the digits 2, 5, 7, 8. So each number occurs \(\frac{96}{4}\) = 24 times.
Now in 100’s place 0 come 24 times. So the remaining digits 2, 5, 7, 8 occurs 96 – 24 = \(\frac{72}{4}\) = 18 times
Similarly in 10’s place and in-unit place 0 occurs 24 times and the remaining digits 2, 5, 7, 8 occurs 18 times.
Now sum of the digits = 2 + 5 + 7 + 8 = 22
Sum in 1000’s place = 22 × 24 = 528
Sum in 100’s, 10’s and in unit place = 22 × 18 = 396
∴ Sum of the 4 digit numbers is

Samacheer Kalvi 11th Maths Solutions Chapter 4 Combinatorics and Mathematical Induction Ex 4.2 Additional Questions

Question 1.

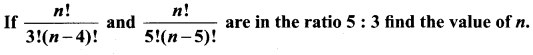
Solution:

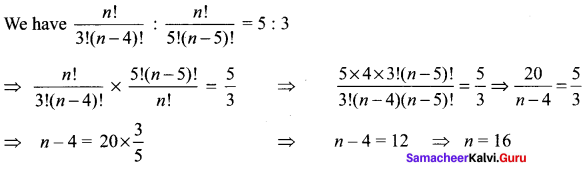
Question 2.
How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7 if no digit is repeated?
Solution:
Here total number of digits = 6
The unit place can be filled with any one of the digits 2, 4, 6.

Question 3.
Find n if ^{n – 1}P₃ : ⁿP₄ = 1 : 9
Solution:

Question 4.
How many words can be formed by using the letters of the word ORIENTAL so that A and E always occupy the odd places?
Solution:
[Hint: There are 4 odd places in the word]

Now the remaining 6 places filled with remaining 6 letters

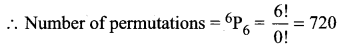
Hence the total number of permutations = 12 × 720 = 8640

Question 5.
Out of 18 points in a plane, no three are in the same line except five points which are collinear. Find the number of lines that can be formed joining the points.
Solution:
Total number of points = 18
Out of 18 numbers, 5 are collinear and we get a straight line by joining any two points.
∴ Total number of straight-line formed by joining 2 points out of 18 points = ¹⁸C₂
Number of straight lines formed by joining 2 points out of 5 points = ⁵C₂
But 5 points are collinear and we get only one line when they are joined pairwise.
So, the required number of straight lines are

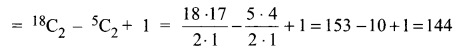
Hence, the total number of straight lines = 144

Question 6.
We wish to select 6 person from 8 but, if the person A is chosen, then B must be chosen. In how many ways can selections be made?
Solution:
Total number of persons = 8
Number of persons to be selected = 6
Condition is that if A is chosen, B must be chosen

Case I: When A is chosen, B must be chosen
Number of ways = ⁶C₄
[∴ A and B are set to be choosen]

Case II: When A is not chosen, then B may be chosen
∴ Number of ways = ⁷C₆

Hence, the required number of ways = 22

Question 7.
How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?
Solution:
For 3-digit even numbers, the unit’s place can be occupied by one of the 3 digits 2, 4 or 6. The remaining 5 digits can be arranged in the remaining 2 places in ⁵P₂ ways.

∴ By the multiplication rule, the required number of 3-digit even numbers is 3 × ⁵P₂ = 3 × 5 × 4 = 60.

Question 8.
Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 if no digit is repeated. How many of these will be even?
Solution:
For 4 digit numbers, we have to arrange the given 5 digits in 4 vacant places. This can be done in ⁵P₄ = 5 × 4 × 3 × 2 = 120 ways.

For 4-digit even numbers, the unit’s place can be occupied by one of the 2 digits 2 or 4. The remaining 4 digits can be arranged in the remaining 3 places in ⁴P₃ ways.
∴ By the multiplication rule, the required number of 4-digit even numbers is 2 × ⁴P₃ = 2 × 4 × 3 × 2 = 48.

Question 9.
Find r if

(i) ⁵P_r = 2 ⁶P_{r – 1} 4
Solution:

(ii) ⁵P_r = ⁶P_{r – 1}

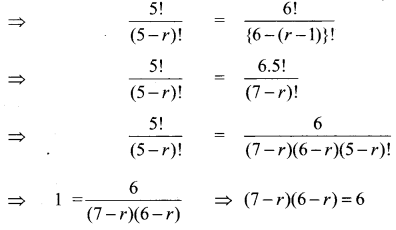
⇒ 42 – 13r + r² = 6 ⇒ r² – 13r + 36 = 0
⇒ (r – 4)(r – 9) = 0 ⇒ r = 4, 9
Now, we know that ⁿP_r is meaningful only when r ≤ n.
∴ ⁵P_r and ⁶P_{r – 1} are meaningless when r ≤ 9.
∴ Rejecting r = 9, we have r = 4

Question 10.
How many words, with or without meaning, can be made from the letters of the word MONDAY, assuming that no letter is repeated, if

(i) 4 letters are used at a time
(ii) all letters are used at a time
(iii) all letters are used but first letter is a vowel?
Solution:
The word MONDAY has 6 distinct letters.

(i) 4 letters out of 6 can be arranged in ⁶P₄ ways.
∴ The required number of words = ⁶P₄ = 6 × 5 × 4 × 3 = 360

(ii) 6 letters can be arranged among themselves in 6P6 ways.
∴ The required number of words = ⁶P₆ = 6! = 1 × 2 × 3 × 4 × 5 × 6 = 720.

(iii) The first place can be filled by anyone Of the two vowels O or A in 2 ways. The remaining 5 letters can be arranged in the remaining 5 places II to VI in ⁵P₅ = 5! ways.
∴ By the multiplication rule, the required number of words = 2 × 5! = 2 × 1 × 2 × 3 × 4 × 5 = 240