You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 7 Matrices and Determinants Ex 7.5
Choose the correct or the most suitable answer from the given four alternatives.
Question 1.
If aij = \(\frac{1}{2}\) (3i – 2j) and A = [aij]2×2 is
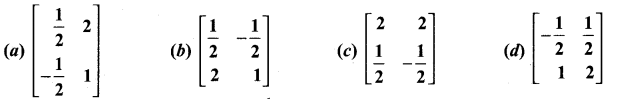
Solution:
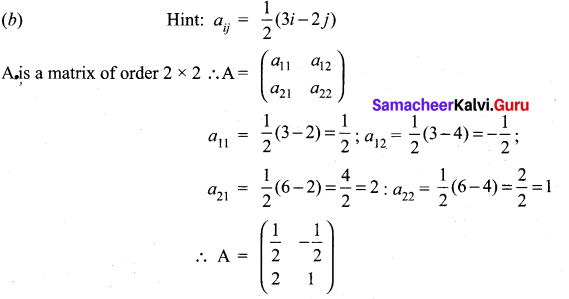
Question 2.
What must be the matrix X, if 2X + \(\left[\begin{array}{ll}{1} & {2} \\ {3} & {4}\end{array}\right]=\left[\begin{array}{ll}{3} & {8} \\ {7} & {2}\end{array}\right]\) ?
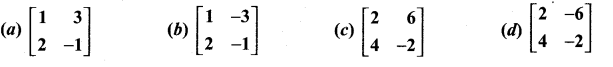
Solution:

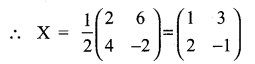
Question 3.
Which one of the following is not true about the matrix \(\left[\begin{array}{lll}{1} & {0} & {0} \\ {0} & {0} & {0} \\ {0} & {0} & {5}\end{array}\right]\)?
(a) a scalar matrix
(b) a diagonal matrix
(c) an upper triangular matrix
(d) A lower triangular matrix
Solution:
(b) a diagonal matrix
![]()
Question 4.
If A and B are two matrices such that A + B and AB are both defined, then …………
(a) A and B are two matrices not necessarily of same order.
(b) A and B are square matrices of same order.
(c) Number of columns of a is equal to the number of rows of B.
(d) A = B.
Solution:
(b) A and B are square matrices of same order.
Question 5.
If A = \(\left[\begin{array}{rr}{\lambda} & {1} \\ {-1} & {-\lambda}\end{array}\right]\), then for what value of λ, A2 = 0?
(a) 0
(b) ±1
(c) -1
(d) 1
Solution:
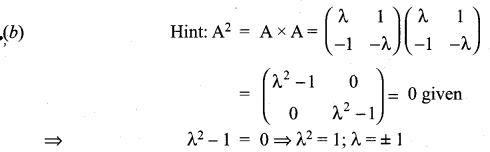
Question 6.
If 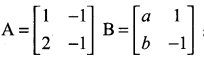 and (A + B)2 = A2 + B2, then the values of a and b are ……………….
and (A + B)2 = A2 + B2, then the values of a and b are ……………….
(a) a = 4, b = 1
(b) a = 1, b = 4
(c) a = 0, b = 4
(d) a = 2, b = 4
Solution:
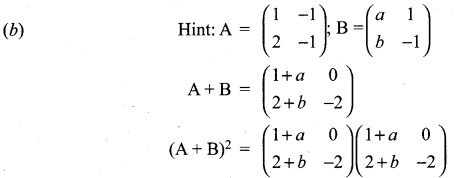
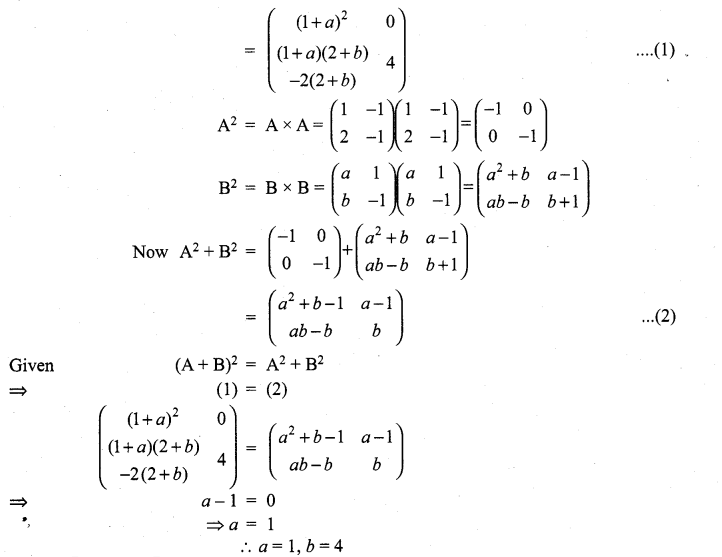
Question 7.
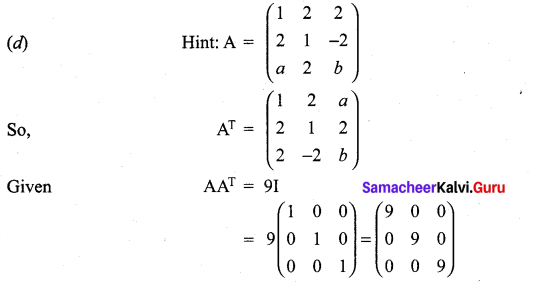
If 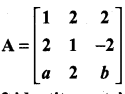 is a matrix satisfying the equation AAT = 9I, where I is 3 × 3 identity matrix, then the ordered pair (a, b) is equal to ………….
is a matrix satisfying the equation AAT = 9I, where I is 3 × 3 identity matrix, then the ordered pair (a, b) is equal to ………….
(a) (2, -1)
(b) (-2, 1)
(c) (2, 1)
(d) (-2, -1)
Solution:
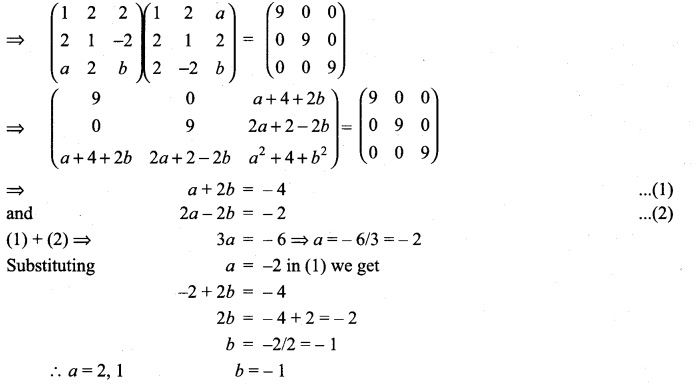
Question 8.
If A is a square matrix, then which of the following is not symmetric?
(a) A + AT
(b) AAT
(c) ATA
(d) A – AT
Solution:
(b) AAT
Question 9.
If A and B are symmetric matrices of order n, where (A ≠ B), then …………….
(a) A + B is skew-symmetric
(b) A + B is symmetric
(c) A + B is a diagonal matrix
(d) A + B is a zero matrix
Solution:
(b) A + B is symmetric
![]()
Question 10.
If 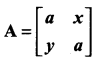 and if xy = 1, then det (AAT) is equal to …………..
and if xy = 1, then det (AAT) is equal to …………..
(a) (a – 1)2
(b) (a2 + 1)2
(c) a2 – 1
(d) (a2 – 1)2
Solution:
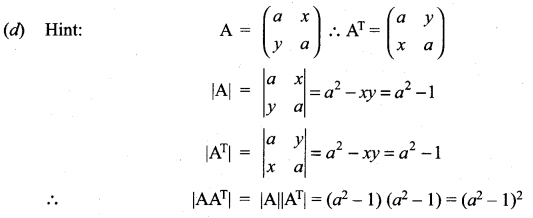
Question 11.
The value of x, for which the matrix 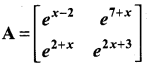 is singular is ………….
is singular is ………….
(a) 9
(b) 8
(c) 7
(d) 6
Solution:
(b) Hint: Given A is a singular matrix ⇒ |A| = 0
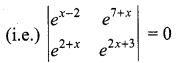
⇒ ex-2.e2x+3 – e2+x.e7+x = 0
⇒ e3x+1 – e9+2x = 0
⇒ e3x+1 = e9+2x
⇒ 3x + 1 = 9 + 2x
⇒ 3x – 2x = 9 – 1
⇒ x = 8
Question 12.
If the points (x, -2), (5, 2), (8, 8) are collinear, then x is equal to …………
(a) -3
(b) \(\frac{1}{3}\)
(c) 1
(d) 3
Solution:
(d) Hint: Given that the points are collinear
So, area of the triangle formed by the points = 0

Question 13.

Solution:
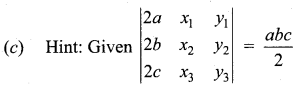

Question 14.
If the square of the matrix 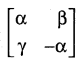 is the unit matrix of order 2, then α, β and γ should satisfy the relation.
is the unit matrix of order 2, then α, β and γ should satisfy the relation.
(a) 1 + α2 + βγ = 0
(b) 1 – α2 – βγ = 0
(c) 1 – α2 + βγ = 0
(d) 1 + α2 – βγ = 0
Solution:
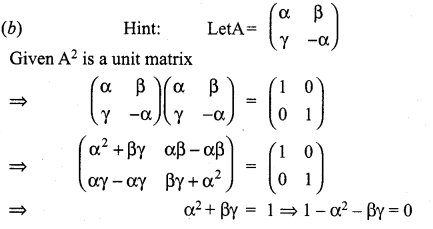
![]()
Question 15.
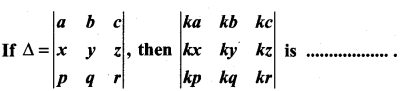
(a) Δ
(b) kΔ
(c) 3kΔ
(d) k3Δ
Solution:
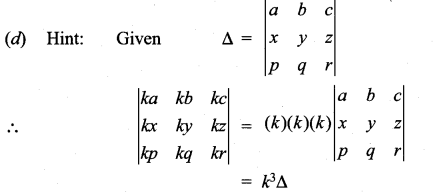
Question 16.
A root of the equation 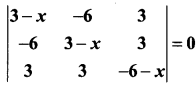 is …………….
is …………….
(a) 6
(b) 3
(c) 0
(d) -6
Solution:
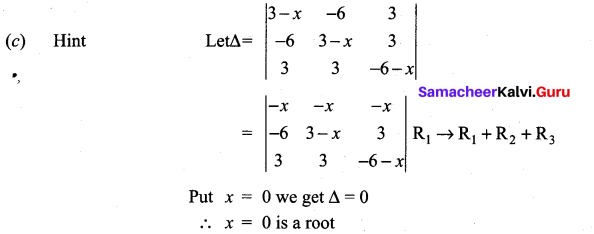
Question 17.
The value of the determinant of 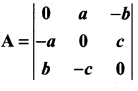 is ……………
is ……………
(a) -2abc
(b) abc
(c) 0
(d) a2 + b2 + c2
Solution:
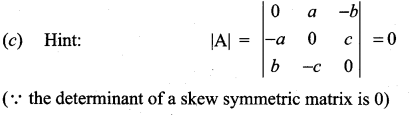
Question 18.
If x1, x2, x3 as well as y1, y2, y3 are in geometric progression with the same common ratio, then the points (x1, y1), (x2, y2), (x3, y3) are
(a) vertices of an equilateral triangle
(b) vertices of a right-angled triangle
(c) vertices of a right-angled isosceles triangle
(d) collinear
Solution:
(d)
Question 19.
If \(\lfloor.\rfloor\) denotes the greatest integer less than or equal to the real number under consideration and -1 ≤ x < 0, 0 ≤ y < 1, 1 ≤ z ≤ 2, then the value of the determinant 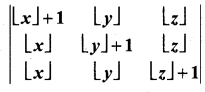 is …………..
is …………..
(a) \(\lfloor z\rfloor\)
(b) \(\lfloor y\rfloor\)
(c) \(\lfloor x\rfloor\)
(d) \(\lfloor x\rfloor+ 1\)
Solution:
(a) Hint: From the given values
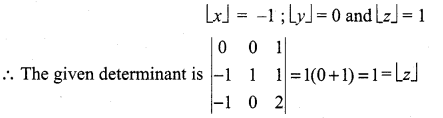 >
>
![]()
Question 20.
If a ≠ b, b, c satisfy 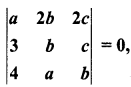 then abc = ……………..
then abc = ……………..
(a) a + b + c
(b) 0
(c) b3
(d) ab + bc
Solution:
(c) Hint: Expanding along R1,
a(b2 – ac) – 2b (3b – 4c) + 2c (3a – 4b) = 0
(b2 – ac) (a – b) = 0
b2 = ac (or) a = b
⇒ abc = b(b2) = b3
Question 21.
If 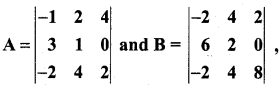 then B is given by ………………..
then B is given by ………………..
(a) B = 4A
(b) B = -4A
(c) B = -A
(d) B = 6A
Solution:

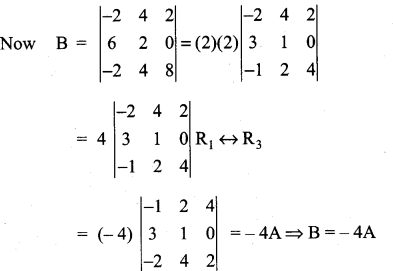
![]()
Question 22.
If A is skew-symmetric of order n and C ¡s a column matrix of order n × 1, then CT AC is ……………..
(a) an identity matrix of order n
(b) an identity matrix of order 1
(e) a zero matrix of order I
(d) an Identity matrix of order 2
Solution:
(c) a zero matrix of order I
Hint: Given A is of order n × n
C is of order n × 1
so, CT is of order 1 × n
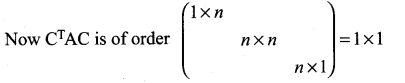
Let it be equal to (x) say
Taking transpose on either side
(CT, AC)T (x)T .
(i.e.) CT(AT)(C) = x
CT(-A)(C) = x
⇒ CTAC = -x
⇒ x = -x
⇒ 2x = 0
⇒ x = 0
Question 23.
The matrix A satisfying the equation 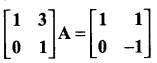 is ……………
is ……………

Solution:
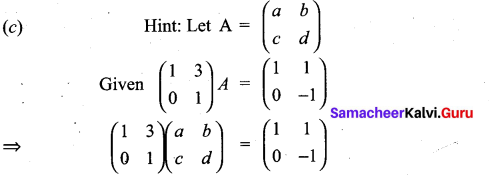
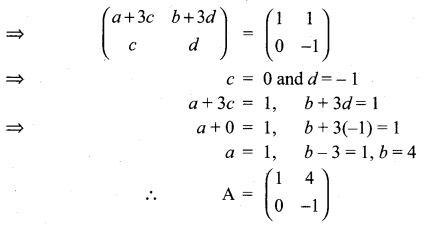
Question 24.
If A + I = 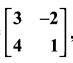 , then (A + I) (A – I) is equal to …………….
, then (A + I) (A – I) is equal to …………….
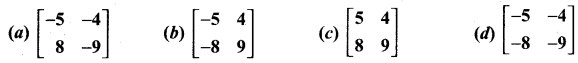
Solution:

Question 25.
Let A and B be two symmetric matrices of the same order. Then which one of the following statements is not true?
(a) A + B ¡s a symmetric matrix
(b) AB ¡s a symmetric matrix
(c) AB = (BA)T
(d) ATB = ABT
Solution:
(b) AB ¡s a symmetric matrix