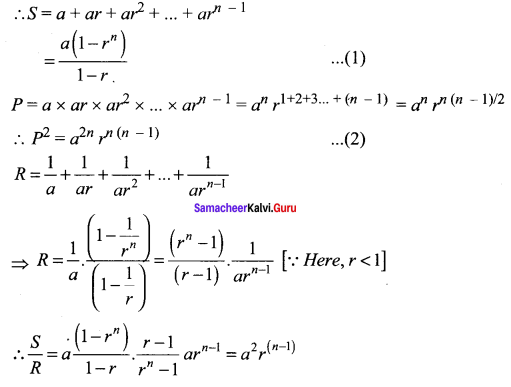You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.3
Question 1.
Find the sum of the first 20-terms of the arithmetic progression having the sum of first 10 terms as 52 and the sum of the first 15 terms as 77.
Solution:
Let ‘a’ be the first term and d be the common difference of A.P.
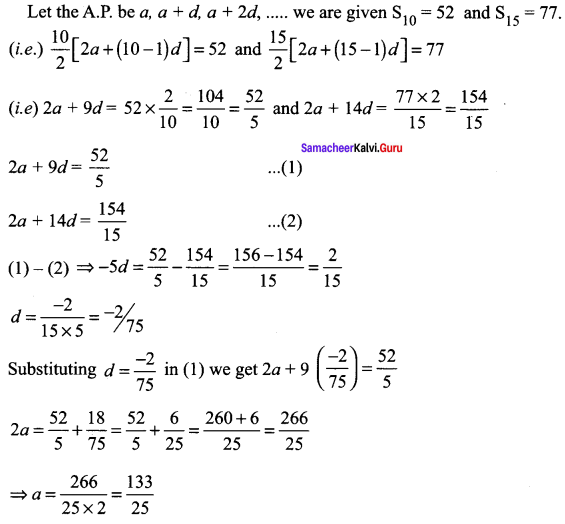
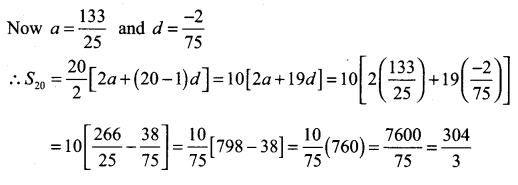
Question 2.

Solution:
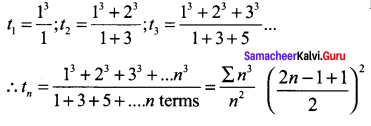

Question 3.
Compute the sum of first n terms of the following series:
(i) 8 + 88 + 888 + 8888 + ……
(i) 6 + 66 + 666 + 6666 + …..
Solution:


Question 4.
Compute the sum of first n terms of 1 + (1 + 4) + (1 + 4 + 42) + (1 + 4 + 42 + 43) + ……..
Solution:

![]()
Question 5.
Find the general term and sum to n terms of the sequence \(1, \frac{4}{3}, \frac{7}{9}, \frac{10}{27}, \ldots \ldots \ldots\)
Solution:
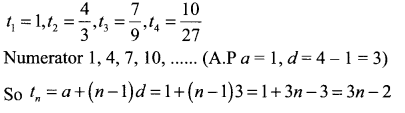
Denominator 1, 3, 9, 27, which is a G.P. a = 1, r = 3
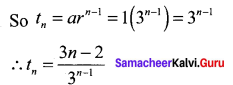
It is an arithmetico Geometric series. Here the nth term is tn = [a + (n – 1)d]rn – 1 where a = 1, d = 3 and r = 1/3
Now the sum to n terms is
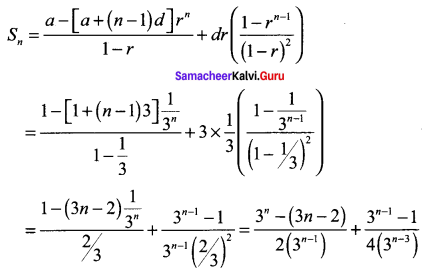
Question 6.
![]()
Solution:

Question 7.
Show that the sum of (m + n)th and (m – n)th term of an A.P. is equal to twice the mth term.
Solution:
The nth term of an A.P is Tn = a + (n – 1) d
Tm+n = a + (m + n – 1) d
Tm-n = a + (m – n – 1) d
Tm+n + Tm-n = a + (m + n – 1) d + a + (m – n – 1)d
= 2a + [m + n – 1 + m – n – 1) d
= 2a + [2m – 2] d
= 2a + 2 (m – 1) d
= 2 [a + (m – 1] d
Tm+n + Tm-n = 2Tm
Hence the sum of the ( m + n)th term and ( m – n)th term of A.P is equal to twice the mth term.
Question 8.
A man repays an amount of ₹ 3250 by paying ₹ 20 in the first month and then increases the payment by ₹ 15 per month. How long will it take him to clear the amount?
Solution:
a = 20, d = 15, Sn = 3250 to find n.

3n2 + 5n – 1300 = 0
3n2 – 60n + 65n – 1300 = 0
3n (n – 20) + 65 (n – 20) = 0
(3n + 65) (n – 20) = 0
n = – 65/3 or 20
n = – 65/3 is not possible
∴ n = 20
So he will take 20 months to clear the amount.
![]()
Question 9.
In a race, 20 balls are placed in a line at intervals of 4 meters with the first ball 24 meters away from the starting point. A contestant is required to bring the balls back to the starting place one at a time. How far would the contestant run to bring back all balls?
Solution:
t1 = 24 × 2 = 48, t2 =48 + 8 = 56 or (24 + 4)2, t3 =(28 + 4)2 = 64 which is an A.P.
Here a = 48,
d = 56 – 48 = 8
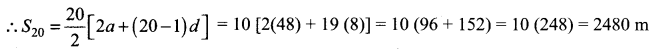
The contestant has to run 2480 m to bring all the balls.
Question 10.
The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of the 2nd hour, 4th hour, and nth hour?
Solution:
Number of bacteria present initially = 30
Number of bacteria at the end of 1 hour = 2 × 30 = 60
Number of bacteria at the end of two hours = 2 × 60 = 120
Number of bacteria at the end of three hours = 2 × 120 = 240
Number of bacteria at the end of four hours = 2 × 240 = 480
![]()
∴ The sequence of a number of bacterias at the end of every hour is
30, 60, 120, 240, 480, …………………………..
30, 30 × 2, 30 × 4, 30 × 8, 30 × 16, …………………
30, 30 × 2, 30 × 22, 30 × 23, 30 × 24, …………………
This sequence is a Geometric sequence with first term a = 30, common ratio r = 2
Number of bacteria at the end of nth hour tn+1 = a. rn
tn+1 = 30(2n)
Number of bacteria at the end of 2nd hour = 120
Number of bacteria at the end of 4th hours = 480
Number of bacteria at the end of nth hour = 30(2n)
Question 11.
What will ₹ 500 amount to in 10 years after its deposit in a bank which pays an annual interest rate of 10% compounded annually?
Solution:

![]()
Question 12.
In a certain town, a viral disease caused severe health hazards upon its people disturbing their normal life. It was found that on each day, the virus which caused the disease spread in Geometric Progression. The amount of infectious virus particle gets doubled each day, being 5 particles on the first day. Find the day when the infectious virus particles just grow over 1,50,000 units?
Solution:
a = 5, r = 2, tn >150000, To find ‘n’
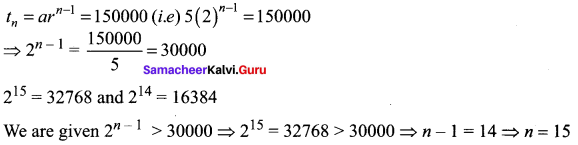
On the 15th day it will grow over 150000 units.
Samacheer Kalvi 11th Maths Solutions Chapter 5 Binomial Theorem, Sequences and Series Ex 5.3 Additional Questions
Question 1.
If the ratio of the sums of m terms and n terms of an A.P. be m2 : n2, prove that the ratio of its mth and nth terms is (2m – 1) : (2n – 1).
Solution:
Let ‘a’ be the first term and d be the common difference of A.P.

⇒ 2an + (mn – n)d = 2am + (mn – m)d
⇒ 2an – 2am = (mn – m – mn + n)d
⇒ 2a(n – m) = (n – m)d ⇒ d = 2a, [n – m ≠ 0, as n ≠ m]
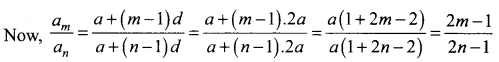
Hence, the required ratio is (2m – 1) : (2n – 1)
Question 2.
Determine the number of terms of geometric progression {an} if a1 = 3, an = 96, Sn = 189.
Solution:

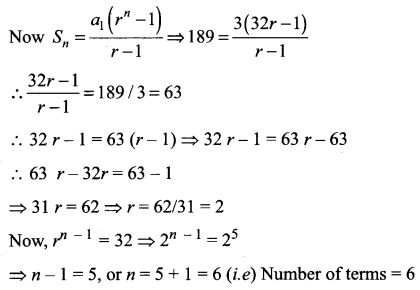
Question 3.
The sum of first three terms of a G.P. is to the sum of the first six terms as 125 : 152. Find the common ratio of the G.P.
Solution:

Hence, the common ratio of the G.P. is \(\frac{3}{5}\)
Question 4.
Find the sum to n terms the series: (x + y) + (x2 + xy + y2) + (x3 + x2y + xy2 + y3) + …
Solution:
(x + y) + (x2 + xy + y2) + (x3 + x2y + xy2 + y3) + … to n terms

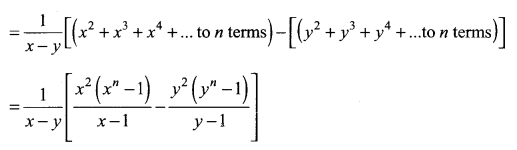
Question 5.
Sum the series: (1 + x) + (1 + x + x2) + (1 + x + x2 + x3) + … up to n terms
Solution:

![]()
Question 6.
Sum up to n terms the series: 7 + 77 + 777 + 7777 + …
Solution:
S = 1 + 77 + 777 + 7777 + … to n terms
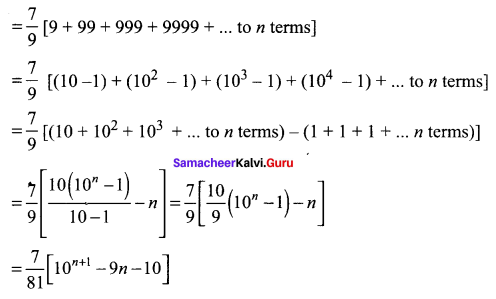
Question 7.
If S1, S2, S3 be respectively the sums of n, 2n, 3n, terms of a G.P. , then prove that S1(S3 – S2) = (S2 – S1)2.
Solution:
Let a be the first term and r be the common ratio of G.P.
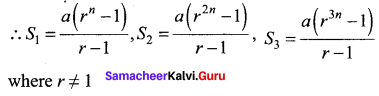
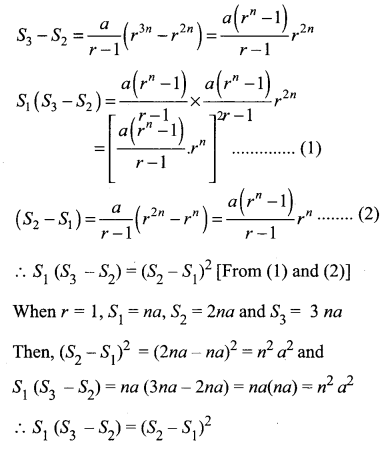
Question 8.
If the sum of the n terms of a G.P be S, their product P and the sum of their reciprocals R, the prove that \(P^{2}=\left(\frac{S}{R}\right)^{n}\)
Solution:
Let a be the first term and r be the common ratio of the G.P.