Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.4

Students can Download Maths Chapter 2 Measurements Ex 2.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.4

Miscellaneous Practice Problems

Question 1.
The base of the parallelogram is 16 cm and the height is 7 cm less than its base. Find the area of the parallelogram.
Solution:
In a parallelogram
Given base b = 16 cm; height h = base – 7 cm = 16 – 7 = 9 cm
Area of the parallelogram = (base × height) sq. units
= 16 × 9 cm² = 144 cm²
Area of the parallelogram = 144 cm²

Question 2.
An agricultural field is in the form of a parallelogram, whose area is 68.75 sq. hm. The distance between the parallel sides is 6.25 cm. Find the length of the base.
Solution:
Height of the parallelogram = 6.25 hm
Area of the parallelogram = 68.75 sq. hm
b × h = 68.75
b × 6.25 = 68.75
b = \(\frac{68.75}{6.25}=\frac{6875}{625}\) = 11 km
Length of the base = 11 km.

Question 3.
A square and a parallelogram have the same area. If the side of the square is 48m and the height of the parallelogram is 18 m. Find the length of the base of the parallelogram.
Solution:
Given side of the square is 48 m
Area of the square = (side × side) sq. unit = 48 × 48 m²
Height of the parallelogram = 18 m
Area of the parallelogram = ‘bh’ sq. units = b × 18 m²
Also area of the parallelogram = Area of the square
b × 18 = 48 × 48
b = \(\frac{{48} \times 48}{18 }\) = 8 × 16 = 128 m
Base of the parallelogram = 128 m

Question 4.
The height of the parallelogram is one fourth of its base. If the area of the parallelogram is 676 sq. cm, find the height and the base.
Solution:
Let the base of the parallelogram be ‘b’ cm
Given height = \(\frac{1}{4}\) × base ; Area of the parallelogram = 676 sq. cm
b × h = 676
b × \(\frac{1}{4}\)b = 676
b × b = 676 × 4
b × b = 13 × 13 × 4 × 4
b = 13 × 4 cm = 52 cm
Height = \(\frac{1}{4}\) × 52 cm = 13 cm
Height = 13 cm, Base 52 cm

Question 5.
The area of the rhombus is 576 sq. cm and the length of one of its diagonal is half of the length of the other diagonal then find the length of the diagonal.
Solution:
Let one diagonal of the rhombus = d₂ cm
The other diagonal d₂ = \(\frac{1}{2}\) × d₁ cm
Area of the rhombus = 576 sq. cm
\(\frac{1}{2}\) × (d₁ × d₂) = 576
\(\frac{1}{2}\) × (d₁ × \(\frac{1}{2}\) d₁) = 576
d₁ × d₁ = 576 × 2 × 2 = 6 × 6 × 4 × 4 × 2 × 2
d₁ × d₁ = 6 × 4 × 2 × 6 × 4 × 2
d₁ = 6 × 4 × 2
d₁ = 48 cm
d₂ = \(\frac{1}{2}\) × 48 = 24 cm
∴ Length of the diagonals d₁ = 48 cm and d₂ = 24 cm.

Question 6.
A ground is in the form of isoceles trapezium with parallel sides measuring 42 m and 36 m long. The distance between the parallel sides is 30 m. Find the cost of levelling it at the rate of ₹ 135 per sq. m.
Solution:
Parallel sides of the trapezium a = 42 m; b = 36 m
Also height h = 30 m
Area of the trapezium = \(\frac{1}{2}\) × h × (a + b) sq. unit
= \(\frac{1}{2}\) × 30 × (42 + 36) m²
= \(\frac{1}{2}\) × 30 × 78 m²
Area = 1,170 m²
Cost of levelling 1 m² = ₹ 135
∴ Cost of levelling 1170 m² = ₹ 1170 × 135 = ₹ 1,57,950
Cost of levelling the ground = ₹ 1,57,950

Challenge Problems

Question 7.
In a parallelogram PQRS (See the diagram) PM and PN are the heights corresponding to the sides QR and RS respectively. If the area of the parallelogram is 900 sq. cm and the length of PM and PN are 20 cm and 36 cm respectively, find the length of the sides QR and SR.

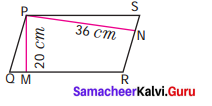
Solution:
Considering QR as base of the parallelogram height h₁ = 20 cm
Area of the parallelogram = 900 cm²
b₁ × h₁ = 900 ; b₁ × 20 = 900
b₁ = \(\frac{900}{20}\) = 45 cm
Again considering SR as base height = 36 cm ; Area = 900 cm²
b₂ × h₂ = 900 ; b₂ × 36 = 900
b₂ = \(\frac{900}{36}\)
b₂ = 25 cm
SR = 25 cm; QR = 45 cm ; SR = 25 cm

Question 8.
If the base and height of a parallelogram are in the ratio 7:3 and the height is 45 cm, then fixed the area of the parallelogram.
Solution:
Given base; height = 7 : 3
Let base = 7x cm
height = 3x cm
also given height = 45 cm
3x = 45 cm 45 .
x = \(\frac{45}{3}\) = 15
Now base = 7x cm = 7 × 15 cm = 105 cm
Area of the parallelogram = b × h sq. unit
= 105 × 45 = 4725 cm²
= 4725 cm²

Question 9.
Find the area of the parallelogram ABCD if AC is 24 cm and BE = DF = 8 cm.

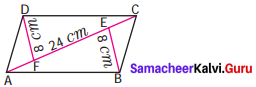
Solution:
Area of the parallelogram ABCD Area of the triangle =Area of the triangle ABC + Area of the triangle ADC

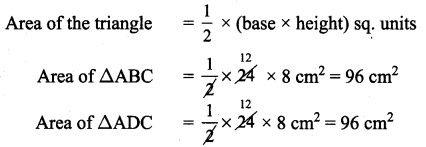
Area of the parallelogram ABCD = 96 + 96 = 192 cm²

Question 10.
The area of the parallelogram ABCD is 1470 sq. cm. If AB = 49 cm and AD = 35 cm then, find the height, DF and BE.

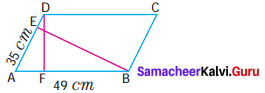
Solution:
Area of the parallelogram = 1470 sq. cm
Considering AB = base = 49 cm
height = DF
Area = base × height
49 × DF = 1470
DF = \(\frac{1470}{49}\)
DF = 30 cm
Now considering AD as base
Base = AD = 35 cm ; height = BE
Base × Height = 1470
35 × BE = 1470 : BE = \(\frac{1470}{35}\)
BE = 42 cm ; DF = 30 cm ; BE = 42 cm

Question 11.
One of the diagonals of a rhombus is thrice as the other. If the sum of the length of the diagonals is 24 cm, then find the area of the rhombus.
Solution:
Let one of the diagonals of rhombus be ‘d₁’ cm and the other be d₂ cm.
Give d₁ = 3 × d₂
Also d₁ + d₂ = 24 cm
⇒ 3d₂ + d₂ = 24
4d₂ = 24
d₂ = \(\frac{24}{4}\)
d₂ = 6 cm
d₁ = 3 × d₂ = 3 × 6
d₁ = 18 cm
∴ Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq. units
= \(\frac{1}{2}\) × 18 × 6 cm² = 54 cm²
Area of the rhombus = 54 cm²

Question 12.
A man has to build a rhombus shaped swimming pool. One of the diagonal is 13 m and the other is twice the first one. Then find the area of the swimming pool and also find the cost of cementing the floor at the rate of ₹ 15 per sq. cm.
Solution:
Let the first diagonal d₁ = 13 m
d₂ = 2 × 13 m = 26 m
Area of the rhombus = \(\frac{1}{2}\) × d₁ × d₂ sq. units
= \(\frac{1}{2}\) × 13 × 26 m² = 169m²
Cost of cementing 1 m² = ₹ 15
Cost of cementing 169 m² = ₹ 169 × 15 = ₹ 2,535
Cost of cementing = ₹ 2,535

Question 13.
Find the height of the parallelogram whose base is four times the height and whose area is 576 sq. cm.
Solution:
Let the height be ‘A’ and base be ‘h’ units
Given b = 4 × h
Area of the parallelogram = 576 sq. cm
b × h = 576
4h × h = 576
h × h = \(\frac{576}{4}\) = 144
h × h = 12 × 12
h = 12 cm
Height = 12 cm; base = 4 × 12 = 48 cm

Question 14.
The table top is in the shape of a trapezium with measurements given in the figure. Find the cost of the glass used to cover the table at the rate of ₹ 6 per 10 sq. cm.

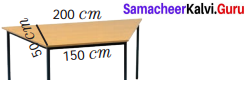
Solution:
Length of the parallel sides a = 200 cm
b = 150 cm
Height h = 50 cm
Area of the trapezium = \(\frac{1}{2}\) × h (a + b) sq. units
= \(\frac{1}{2}\) × 50 (200+ 150) cm²
= \(\frac{1}{2}\) × 50 × 350 cm² = 8750 cm²
Cost for 10 sq. cm glass = ₹ 68
∴ Cost of 8750 cm² glass = \(\frac{8750}{10}\) × 6 = ₹ 5250
Cost of glass used = ₹ 5,250

Question 15.
Arivu has a land ABCD with the measurements given in the figure. If a portion ABED is used for cultivation (where E is the midpoint of DC). D Find the cultivated area.

Solution:
From the figure given ABED is a trapazium with height h = 18 m
One of the parallel side a = 24 m
Since E is the midpoint of D.
Other parallel side b = \(\frac{24}{2}\) = 12 m
Area of the cultivated ADEB = \(\frac{1}{2}\) × h(a + b) m² = \(\frac{1}{2}\) × 18 (24 + 12)
= 9 × 36 m² = 324 m²
Area of cultivation = 324 m²