Students can Download Maths Chapter 2 Measurements Ex 2.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.3
Question 1.
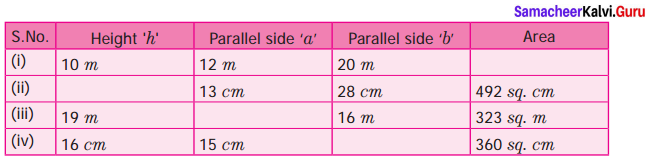
Find the missing values.
Solution:
(i) Given Height h = 10 m ; Parallel sides a = 12 m ; b = 20 m
Area of the Trapezium = \(\frac{1}{2}\)h(a + b) sq. units = \(\frac{1}{2}\) × 10 × (12 + 20)m2
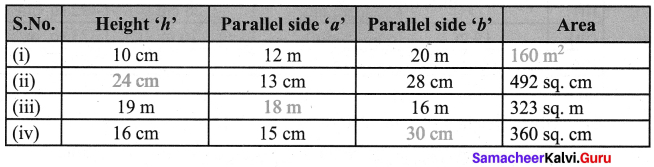
= (5 × 32)m2 = 160 m2
(ii) Given the parallel sides a = 13 cm ; 6 = 28 cm
Area of the trapezium = 492 sq. cm
\(\frac{1}{2}\)h(a + b) = 492
\(\frac{1}{2}\) × h × (13 + 28) = 492
h × 41 = 492 × 2
h = \(\frac { 492\times 2 }{ 41 } \)
h = 24 cm
(iii) Given height ‘h’ = 19 m; Parallel sides b = 16 m
Area of the trapezium = 323 sq. m
\(\frac{1}{2}\)h(a + b) = 323
\(\frac{1}{2}\) × h × (a + 16) = 323
a + 16 = \(\frac { 323\times 2 }{ 19 } \) = 34
a = 34 – 16 = 18 m
a = 18 m
(iv) Given the height h- 16 cm ; Parallel sides a = 15 cm
Area of the trapezium = 360 sq. cm
\(\frac{1}{2}\) × h × (a + b) = 360
\(\frac{1}{2}\) × 16 × (15 + 6) = 360
15 + b = \(\frac{360}{8}\) =45
b = 45 – 15 = 30
b = 30 cm
Tabulating the results we get
Question 2.
Find the area of a trapezium whose parallel sides are 24 cm and 20 cm and the distance between them is 15 cm.
Solution:
Given the parallel sides a = 24 cm; b = 20 cm
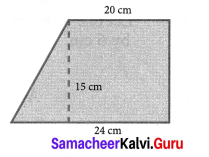
Distance between a and b is ‘h’ = 15 cm
Area of the trapezium = \(\frac{1}{2}\) × h × (a + b) sq. units
= \(\frac{1}{2}\) × 15 × (24 + 20) cm2
= \(\frac{1}{2}\) × 15 × 44 = 330 cm2
Area of the trapezium = 330 cm2
Question 3.
The area of a trapezium is 1586 sq. cm. The distance between its parallel sides is 26 cm. If one of the parallel sides is 84 cm then find the other side.
Solution:
Given one parallel side = 84 cm. Let the other parallel side be ‘b’ cm.
Distance between a and b is h = 26 cm.
Area of the trapezium = 1586 sq. cm
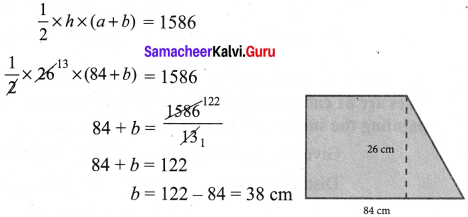
∴ The other parallel side = 38 cm.
Question 4.
The area of a trapezium is 1080 sq. cm. If the lengths of its parallel sides are 55.6 cm and 34.4 cm. Find the distance between them.
Solution:
Length of the parallel sides a = 55.6 cm ; b = 34.4 cm
Area of the trapezium = 1080 sq. cm
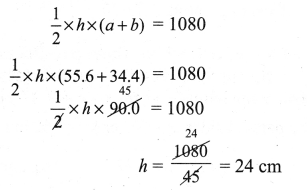
Distance between parallel sides = 24 cm.
![]()
Question 5.
The area of a trapezium is 180 sq. cm and its height is 9 cm. If one of the parallel sides is longer than the other by 6 cm. Find the length of the parallel sides.
Solution:
Let one of the parallel side be ‘a’ cm. Given one parallel sides is longer than the other by 6 cm.
i.e. b = a + 6 cm Also given height ‘h’ = 9 cm
Area of trapezium = 180 sq. cm
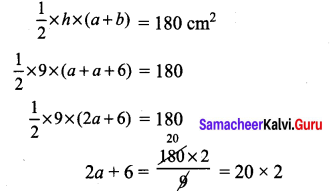
2a + 6 = 40
2a = 40 – 6 = 34
a = \(\frac{34}{2}\) = 17 cm
b = a + 6= 17 + 6 = 23 cm
∴ The parallel sides are a = 17 cm and b = 23 cm
Question 6.
The sunshade of a window is in the form of isoceles trapezium whose parallel sides are 81 cm and 64 cm and the distance between them is 6 cm. Find the cost of painting the surface at the rate of ₹ 2 per sq. cm.
Solution:
Given the parallel sides a = 81 cm ; b = 64 cm
Distance between ‘a’ and ‘b’ is height h = 6 cm
Area of the trapezium = \(\frac{1}{2}\) × h(a + b) sq. units
= \(\frac{1}{2}\) × 63 × (81 + 64) = 3 × 145 cm2 = 435 cm2
Cost of painting 1 cm2 = ₹ 2
Cost of painting 435 cm2 = ₹ 435 × 2 = ₹ 870
Cost of painting = ₹ 870 .
Question 7.
A window is in the form of trapezium whose parallel sides are 105 cm and 50 cm respectively and the distance between the parallel sides is 60 cm. Find the cost of the glass used to cover the window at the rate of ₹ 15 per 100 sq. cm.
Solution:
Given the parallel sides a = 105 cm ; b = 50 cm ; Height = 60 cm
Area of the trapezium = \(\frac{1}{2}\) × h × (a + b)sq. units = \(\frac{1}{2}\) × 60 × (105 + 50) cm2
= 30 × 155 cm2 = 4650 cm2
For 100 cm2 cost of glass used = ₹15
∴ For 4650 cm2 cost of glass = ₹ \(\frac{4650}{100}\) × 15 = ₹ 697.50
Cost of the glass used = ₹ 697.50
Objective Type Questions
Question 8.
The area of the trapezium, if the parallel sides are measuring 8 cm and 10 cm and the height 5 cm is
(i) 45 sq. cm
(ii) 40 sq. cm
(iii) 18 sq. cm
(iv) 50 sq. cm
Solution:
(i) 45 sq. cm
Hint: \(\frac{1}{2}\) × h × (a + b) = \(\frac{1}{2}\) × 5 × (10 + 8) = 45
![]()
Question 9.
In a trapezium if the sum of the parallel sides is 10 m and the area is 140 sq.m, then the height is
(i) 7 cm
(ii) 40 cm
(iii) 14 cm
(iv) 28 cm
Solution:
(iv) 28 cm
Hint: Area = \(\frac{1}{2}\) × h × (a + b) = 140 = \(\frac{1}{2}\) × h × 10 ⇒ h = 28
Question 10.
When the non-parallel sides of a trapezium are equal then it is known as
(i) a square
(ii) a rectangle
(iii) an isoceles trapezium
(iv) a parallelogram
Solution:
(iii) an isoceles trapezium