You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.10
Question 1.
Solve the following quadratic equations by factorization method
(i) 4x2 – 7x – 2 = 0
(ii) 3(p2 – 6) = p(p + 5)
(iii) \(\sqrt{a(a-7)}=3 \sqrt{2}\)
(iv) \(\sqrt{2} x^{2}+7 x+5 \sqrt{2}=0\)
(v) 2x2 – x + \(\frac{1}{8}\) = 0
Solution:
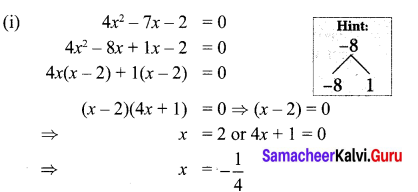
(ii) 3(p2 – 6) = p(p + 5)
3p2 – 18 = p2 + 5p ⇒ 392 – 5p – 18 = 0
⇒ 2p2 – 5p – 18 = 0
⇒ (2p – 9) (p + 2) = 0 ⇒ p = \(\frac{9}{2}\), -2
(iii) \(\sqrt{a(a-7)}=3 \sqrt{2}\)
Squaring on both sides
a(a – 7) = 9 × 2
a2 – 7a – 18 = 0
a2 – 9a + 2a – 18 = 0
a(a – 9) + 2(a – 9) = 0
(a – 9) (a + 2) = 0
⇒ a = 9, a = -2
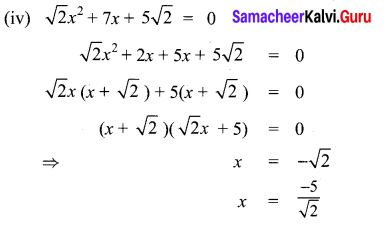
(v) 2x2 – x + \(\frac{1}{8}\) = 0
16x2 – 8x + 1 = 0
16x2 – 4x – 4x + 1 = 0
4x(4x – 1) – 1(4x – 1) = 0
(4x – 1) (4x – 1) = 0
⇒ x = \(\frac{1}{4}, \frac{1}{4}\)
![]()
Question 2.
The number of volleyball games that must be scheduled in a league with n teams is given by G(n) = \(\frac{n^{2}-n}{2}\) where each team plays with every other team exactly once. A league schedules 15 games. How many teams are in the league?
Answer:
Number of games = 15
G(n) = \(\frac{n^{2}-n}{2}\)
\(\frac{n^{2}-n}{2}\) = 15
n2 – n = 30 ⇒ n2 – n – 30 = 0
⇒ n2– 6n – 5n – 30 = 0
(n – 6) (n + 5) = 0
n – 6 = 0 or n + 5 = 0
[Note: – 5 is neglected because number of team is not negative]
n = 6 or n = -5
∴ Number of teams = 6