Students can Download Maths Chapter 5 Geometry Ex 5.6 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Ex 5.6
Miscellaneous Practice Problems
Question 1.
Find the value of x if ∠AOB is a right angle.
Solution:
Given that ∠AOB = 90°
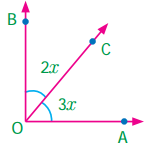
∠AOB = ∠AOC + ∠COB = 90° (Adjacent angles)
3x + 2x = 90°
5x = 90°
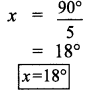
![]()
Question 2.
In the given figure, find the value of x.
Solution:
Since ∠BOC and ∠AOC are linear pair, their sum = 180°
2x + 23 + 3x – 48 = 180°
5x – 25 = 180°
5x – 25 + 25 = 180° + 25
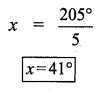
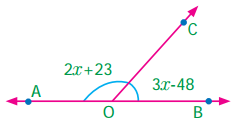
Question 3.
Find the value of x, y and z.
Solution:
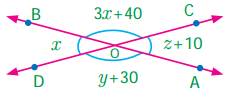
∠DOB and ∠BOC are linear pair
∴ ∠DOB + ∠BOC = 180°
x + 3x + 40 = 180°
4x + 40 = 180°
4x + 40 – 40 = 180° – 40°
4x = 140°
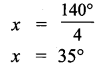
Also ∠BOD and ∠AOC are vertically opposite angles.
∴ ∠BOD = ∠AOC
x = z + 10
35° = z + 10
z + 10 – 10 = 35 – 10
z = 25°
Again ∠AOD and ∠AOC are linear pair.
∴ ∠AOD + ∠AOC = 180°
y + 30 + z + 10 = 180°
y + 30 + 25 + 10 = 180°
y + 65 = 180°
y + 65 – 65 = 180° – 65
y = 115°
∴ x = 35°,
y = 115°,
z = 25°
![]()
Question 4.
Two angles are in the ratio 11 : 25. If they are linear pair, find the angles.
Solution:
Given two angles are in the ratio 11 : 25.
Let the angles be 11x and 25x.
They are also linear pair
∴ 11x + 25x = 180°.
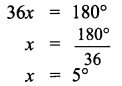
∴ The angles 11x = 11 × 5° = 55° and 25x = 25 × 5 = 125°.
∴ The angles are 55° and 125°.
Question 5.
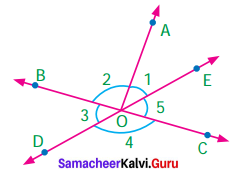
Using the figure, answer the following questions and justify your answer.
(i) Is ∠1 adjacent to ∠2?
(ii) Is ∠AOB adjacent to ∠BOE?
(iii) Does ∠BOC and ∠BOD form a linear pair?
(iv) Are the angles ∠COD and ∠BOD supplementary.
(v) Is ∠3 vertically opposite to ∠1 ?
Solution:
(i) Yes, ∠1 is adjacent to ∠2.
Because they both have the common vertex ‘O’ and the common arm OA . Also their interiors do not overlap.
(ii) No, ∠AOB and ∠BOB are not adjacent angles because they have overlapping interiors.
(iii) No, ∠BOC and ∠BOD does not form a linear pair.
Because ∠BOC itself a straight angle, so the sum of ∠BOC and ∠BOD exceed 180°.
(iv) Yes, the angles ∠COD and ∠BOD are supplementary ∠COD + ∠BOD = 180°, [∵ linear pair of angles]
∴ ∠COD and ∠BOD are supplementary.
(v) No. ∠3 and ∠1 are not formed by intersecting lines. So they are not vertically opposite angles.
![]()
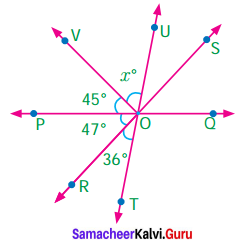
Question 6.
In the figure POQ, ROS and TOU are straight lines. Find the x°.
Solution:
Given TOU is a straight line.
∴ The sum of all angles formed at a point on a straight line is 180°
∠TOR + ∠ROP + ∠POV + ∠VOU = 180°.
36° + 47°+ 45° + x° = 180°.
128° + x° = 180°
128° + x° – 128° = 180° – 128°
x = 52°
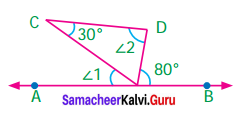
Question 7.
In the figure AB is parallel to DC. Find the value of ∠1 and ∠2. Justify your answer.
Solution:
Given AB || DC
AB and CD are parallel lines Taking CE as transversal we have.
∠1 = 30°, [∵ alternate interior angles]
Taking DE as transversal
∠2 = 80°.[∵ alternate interior angles]
∠1 = 30° and ∠2 = 80°
Justification:
CDE is a triangle
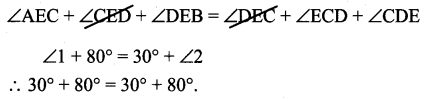
![]()
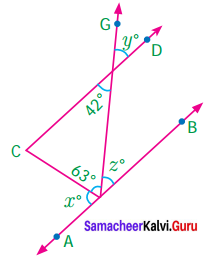
Question 8.
In the figure AB is parallel to CD. Find x, y and z.
Solution:
Given AB || CD
∴ Z = 42 (∵ Alternate interior angles)
Also y = 42° [vertically opposite angles]
Also x° + 63° + z° = 180°
x° + 63° + 42° = 180°
x° + 105° = 180°
x°+ 105° – 105° = 180° – 105°
x° = 75°
∴ x = 75°;
y = 42°;
z = 42°
Question 9.
Draw two parallel lines and a transversal. Mark two alternate interior angles G and H. If they are supplementary, what is the measure of each angle?
Solution:
l and m are parallel lines and n is the transversal.
∠G and ∠H are alternate interior angles.
∠G = ∠H …… (1)
Given ∠G and ∠G are Suplementary
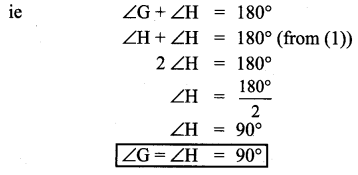
Question 10.
A plumber must install pipe 2 parallel to pipe 1. He knows that ∠1 is 53. What is the measure of ∠2?
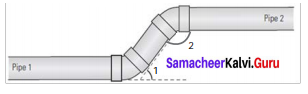
Solution:
Given ∠1 = 53°
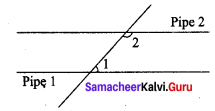
Clearly ∠1 and ∠2 are interior angles on the same side of the transversal and so they are supplementary.
∠1 + ∠2 = 180°
53° + ∠2 = 180°
53° + ∠2 – 53° = 180° – 53°
∠2 = 127°
Challenge Problems
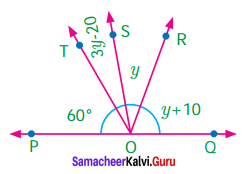
Question 11.
Find the value of y.
Solution:
Cleary POQ is a straight line”
Sum of all angles formed at a point on a straight line is 180°
∴ ∠POT + ∠TOS + ∠SOR + ∠ROQ = 180°
60° + (3y – 20°) + y° + (y + 10°) = 180°
60° + 3y – 20° + y° + y° + 10° = 180°
5y + 50° = 180°
5y + 50° – 50° = 180° – 50
5y = 130°
\(y=\frac{130^{\circ}}{5}\)
y = 26°
![]()
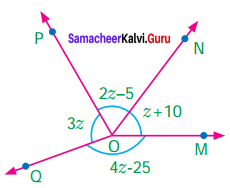
Question 12.
Find the value of z.
Solution:
The sum of angles at a point is 360°.
∴ ∠QOP + ∠PON + ∠NOM + ∠MOQ = 360°
3z + (2z – 5) + (z + 10) + (4z – 25) = 360°
3z + 2z + z + 4z — 5 +10 — 25 = 360°
10z – 20° = 360°
10z – 20° + 20 = 360°+ 2
10z = 380°
\(z=\frac{380^{\circ}}{10}\)
z = 38°
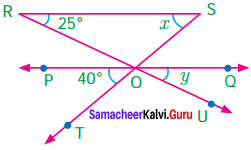
Question 13.
Find the value of x and y if RS is parallel to PQ.
Solution:
Given RS || PQ
Considering the transversal RU, we have y = 25° (corresponding angles)
Considering ST as transversal
Question 14.
Two parallel lines are cut by a transversal. For each pair of interior angles on the same side of the transversal, if one angle exceeds the twice of the other angle by 48°. Find the angles.
Solution:
Let the two parallel lines be m and n and l be the transversal
Let one of the interior angles on the same side of the transversal be x°
Then the other will be 2x + 48.
We know that they are supplementary.
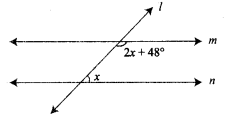

Question 15.
In the figure, the lines GH and IJ are parallel. If ∠1 = 108° and ∠2 = 123°, find the value of x, y and z.
Solution:
Given GH || IZ
∠1 = 108°
∠2 = 123°
∠1 + ∠KGH = 180 [linear pair]
108° + ∠KGH = 180°
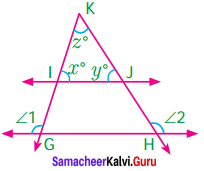
108° + ∠KGH – 108° = 180° – 108°
∠KGH = 72°
∠KGH = x° (corresponding angles if KG is a transversal)
∴ x° = 72°
Similarly
∠2 + ∠GHK = 180° (∵ linear pair)
123° + ∠GHK = 180°
123° + ∠GHK – 123° = 180° – 123°
∠GHK = 57°
Again ∠GHK = y° (corresponding angles if KH is a transversal)
y = 57°
x° +y° + z° = 180° (sum of three angles of a triangle is 180°)
72° + 57° + z° = 180°
129° + z° = 180°
129° + z° – 129° = 180° – 129°
z = 51°
x = 72°,
y = 57°,
z = 51°
Question 16.
In the parking lot shown, the lines that mark the width of each space are parallel. If
∠1 = (2x – 3y)°; ∠2 = (x + 39)° find x° and y°.
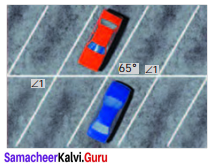
Solution:
From the picture
∠2 + 65° = 180° [Sum of interior angles on the same side of a transversal]
x + 39° + 65° = 180°
x + 104° = 180°
x + 104° – 104° = 180° – 104°
x = 76°
Also from the picture
∠1 = 65° [alternate exterior angles]
2x – 3y = 65°
2 (76) – 3y = 65°
152° – 3y = 65°
152° – 3y – 152° = 65 – 152°
-3y = -87
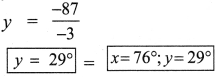
![]()
Question 17.
Draw two parallel lines and a transversal. Mark two corresponding angles A and B. If ∠A = 4x, and ∠B = 3x + 7, find the value of x. Explain.
Solution:
Let m and n are two parallel lines and l is the transversal.
A and B are corresponding angles.
We know that corresponding angles are equals,
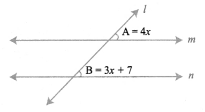
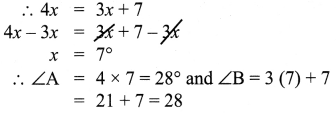
Question 18.
In the figure AB in parallel to CD. Find x°, y° and z°.
Solution:
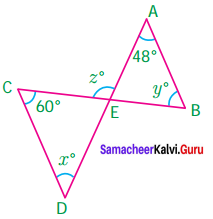
Given AB||CD
Then AD and BC are transversals.
x = 48°, alternate interior angles; AD is transversal y = 60°, alternate interior angles; BC is transversal
∠AEB + 48° + y° = 180°, (sum of angles of a triangle is 180°)

Question 19.
Two parallel lines are cut by transversal. If one angle of a pair of corresponding angles can be represented by 42° less than three times the other. Find the corresponding angles.
Solution:
We know that the corresponding angles are equal.
Let one of the corresponding angles be x.
Then the other will be 3x – 42°.
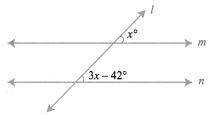

Question 20.
In the given figure, ∠8 = 107°, what is these sum of the angles ∠2 and ∠4.
Solution:
Given ∠8 = 107°
∠2 = 107°
[∵ ∠8 and ∠2 are alternate exterior angles, ∵ ∠8 = ∠2]