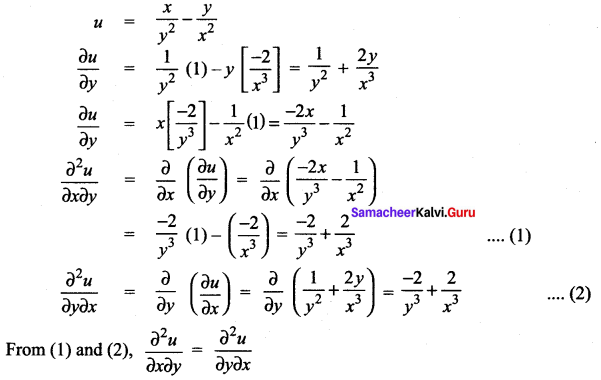You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.4
Question 1.
Find the partial derivatives of the following functions at the indicated points.
(i) f(x, y) = 3x2 – 2xy + y2 + 5x + 2, (2, -5)
(ii) g(x, y) = 3x2 + y2 + 5x + 2, (1, -2)
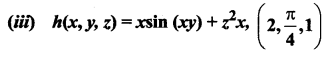
(iv) G (x, y) = e*x + 3y log (x2 + y2), (-1, 1)
Solution:
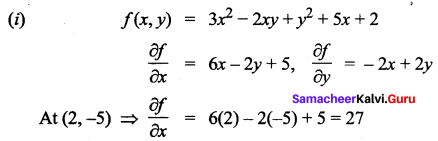

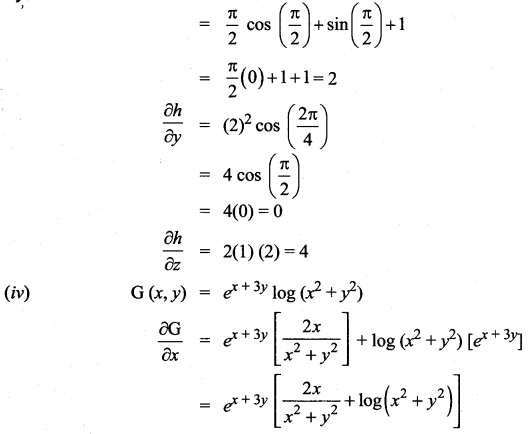

![]()
Question 2.
For each of the following functions find the fx, fy and show that fxy = fyx
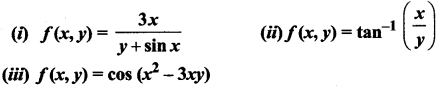
Solution:

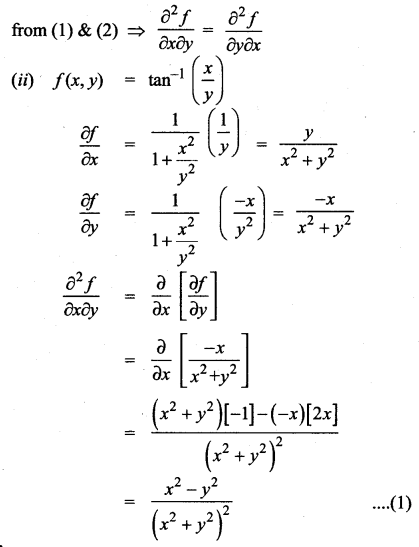

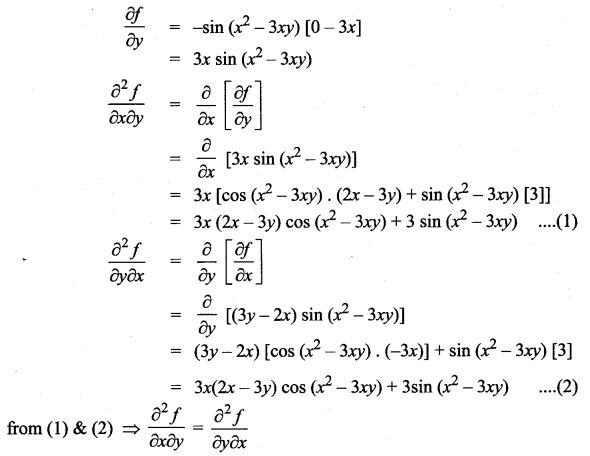
Question 3.
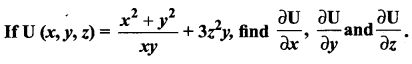
Solution:

![]()
Question 4.
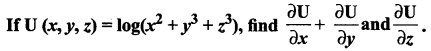
Solution:
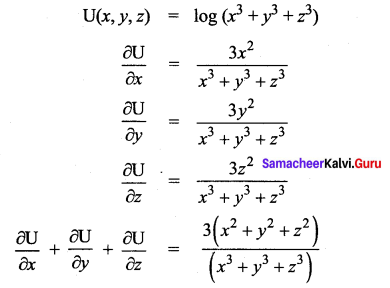
Question 5.
For each of the following functions find the gxy, gxx, gyy and gyx.
(i) g(x, y) = xey + 3x2y
(ii) g(x, y) = log(5x + 3y)
(iii) g(x, y) = x2 + 3xy – 7y + cos(5x)
Solution:

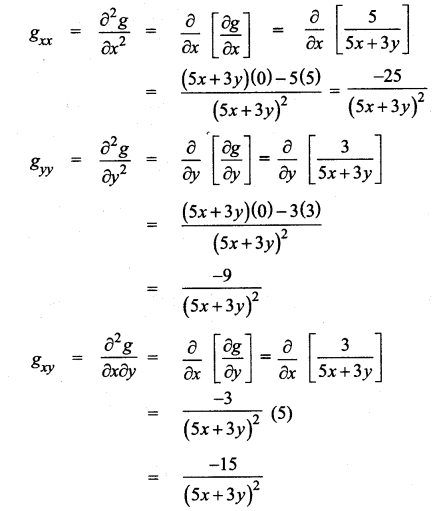
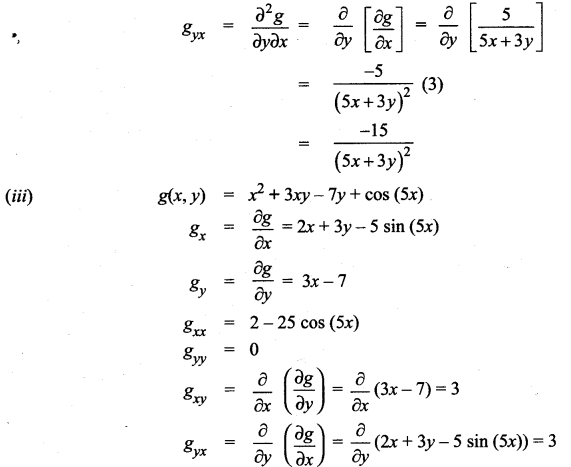
![]()
Question 6.
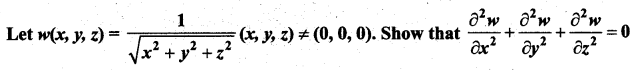
Solution:

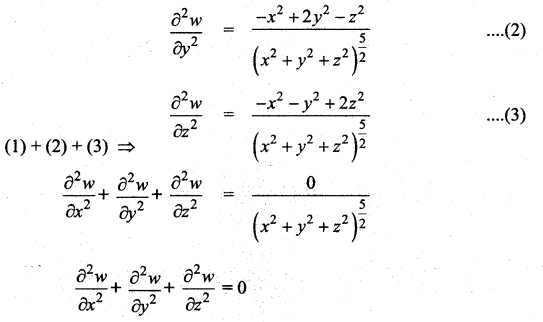
Question 7.
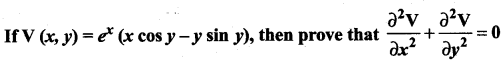
Solution:
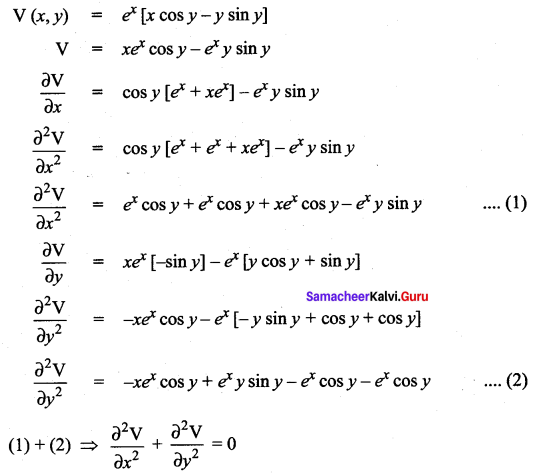
![]()
Question 8.
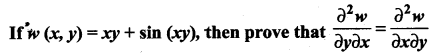
Solution:

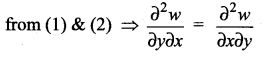
Question 9.
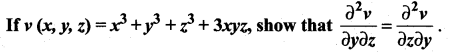
Solution:

![]()
Question 10.
A firm produces two types of calculators each week, x number of type A and j number of type B . The weekly revenue and cost functions (in rupees) are
R(x, y) = 80x + 90y + 0.04xy – 0.05.x2 – 0.05y2 and C(x, y) = 8x + 6y + 2000 respectively.
(i) Find the profit function P(x,y),
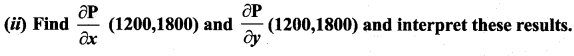
Solution:
(i) P (x, y) = R (x, y) – C (x, y)
= (80x + 90y + 0.04xy – 0.05x² – 0.05y²) – (8x + 6y + 2000)
P (x, y) = 72x + 84y + 0.04xy – 0.05x² – 0.05y² – 2000


Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.4 Additional Problems
Question 1.
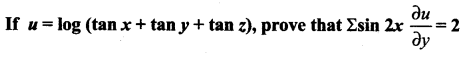
Solution:

![]()
Question 2.
If U = (x – y) (y – z) (z – x) then show that Ux + Uy + Uz = 0
Solution:
Ux = (y – z) {(x – y)(-1) + (z – x). 1}
= (y – z) [(z – x) – (x – y)]
Similarly Uy = (z – x) [(x – y) – (y – z)]
z = (x – y)[(y – z) – (z – x]
Ux + Uy + Uz = (y – z) [(z – x) – (z – x)] + (x – y) [- (y – z) + (y – z)] + (z – x) [(x – y) – (x – y)]
∴ Ux + Uy + Uz = 0.
Hence proved.
Question 3.
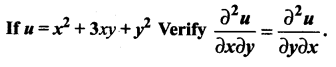
Solution:
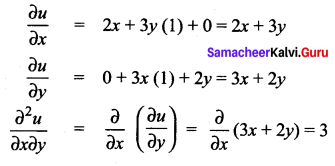
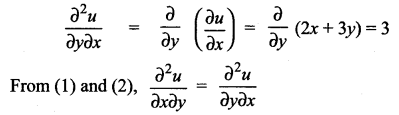
![]()
Question 4.

Solution: