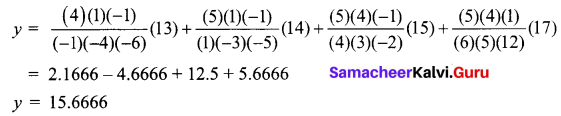Students can download 12th Business Maths Chapter 5 Numerical Methods Additional Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 5 Numerical Methods Additional Problems
One Mark Questions
Question 1.
Match the following.
| (a) ∆f(x) | (i) 2x + 1 |
| (b) E2 f(x) | (ii) 1 + ∆ |
| (c) E | (iii) f(x + h) – f(x) |
| (d) ∆x2, h = 1 | (iv) f(x + 2h) |
Answer:
(a) – (iii), (b) – (iv), (c) – (ii), (d) – (i)
Question 2.
E-n f(x) is ______
(a) f(x + nh)
(b) f(x – nh)
(c) f(-nh)
(d) f(x – n)
Answer:
(b) f(x – nh)
![]()
Question 3.
E is a _____
(a) shifting operator
(b) Displacement operator
(c) 1 + ∆
(d) all of these
(e) none of these
Answer:
(d) all of these
Question 4.
∆4 y3 = _______
(a) (E – 1)4 y3
(b) (E3 – 1) y3
(c) (E – 1)3 y0
(d) (E – 1)4 y0
Answer:
(a) (E – 1)4 y3
![]()
Question 5.
Fill in the blanks.
- The two methods of interpolation are _______ and _______
- If values of x are not equidistant we use _______ method.
- ∆(f(x) + g(x)) = ______
- ∆k yn = ______
- The first three terms in Newton’s method will give a ________ interpolation.
Answer:
- graphical method, algebraic method
- Lagrange’s method
- ∆f(x) + ∆g(x)
- ∆k-1 yn+1 – ∆k-1 yn
- Parabolic
Question 6.
Say true or false
- ∇y2 = y1 – y0
- ∇2 yn = ∇yn – ∇yn+1
- When 5 values are given, the polynomial which fits the data is of degree 4
- E ∆ = ∆ E
- f(2) + ∆f(2) = f(3)
Answer:
- False
- True
- True
- True
- True
II. 2 Mark Questions
Question 1.
Find the missing term from the following data.

Solution:
Since three values of y = f(x) are given, the polynomial which fits the data is of degree two.
Hence third differences are zero.

![]()
Question 2.
From the following data estimate the export for the year 2000

Solution:
Consider a polynomial of degree two.
Hence third differences are zero.

Question 3.
For the tabulated values of y = f(x), find ∆y3 and ∆3y2

Solution:

Question 4.
If f(x) = x2 + ax + b, find ∆r f(x)
Solution:
∆f(x) = f(x + h) – f(x)
= [(x + h )2 + a(x + h) + b] – [x2 + ax + b]
= 2xh + h2 + ah
∆2 f(x) = [2(x + h) h + h2 + ah] – [2xh + h2 + ah] = 2h2
∆3 f(x) = 0
Thus ∆r f(x) = 0 for all r ≥ 3
![]()
Question 5.
Show that ∆3 y4 = ∇3 y7
Solution:
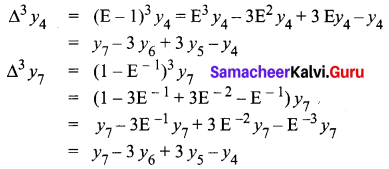
Hence proved
III. 3 and 5 Marks Questions
Question 1.
If f(0) = 5, f(1) = 6, f(3) = 50, f(4) = 105, find f(2) by using Lagrange’s formula.
Solution:


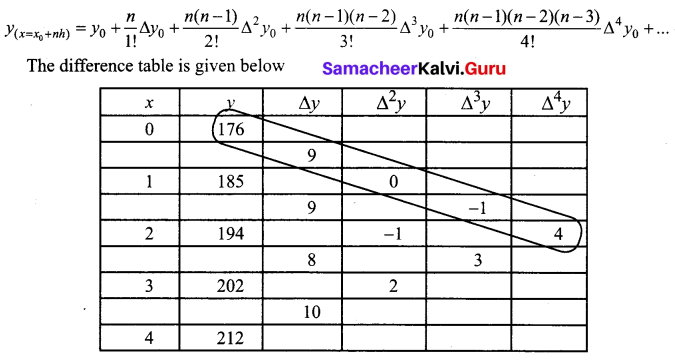
Question 2.
Find y when x = 0.2 given that

Solution:
Since the required value of y is near the beginning of the table, we use Newton’s forward difference formula

![]()
Question 3.
Find the number of men getting wages between Rs.30 and Rs.35 from the following table:

Solution:
The difference table
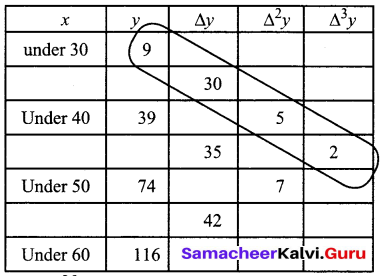

No. of men getting wages less than 35 is 24. Therefore the number of men getting wages between Rs.30 and Rs.35 is y (35) – y (30)
(i.e) 24 – 9 = 15
Question 4.
Using Newton’s formula estimate the population of town for the year 1995:

Solution:
1995 lies in (1991, 2001). Hence we use Newton’s backward interpolation formula.
Here x = 1995, xn = 2001, h = 10
1995 = xn + nh
⇒ 1995 = 2001 + 10n
⇒ n = \(\frac{1995-2001}{10}\)
⇒ n = -0.6
The backward difference table is given below
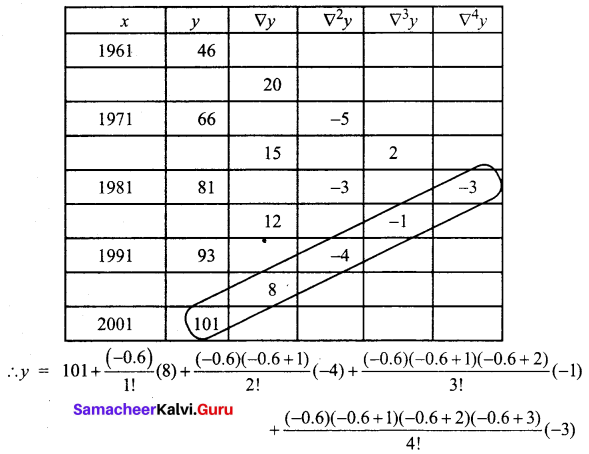
y = 101 – 4.8 + 0.48 + 0.056 + 0.1008
y = 96.8368
Hence the population for the year 1995 is 96.837 thousands.
![]()
Question 5.
Using Lagrange’s formula find y(11) from the following table

Solution:
Given
x0 = 6, y0 = 13
x1 = 7, y1 = 14
x2 = 10, y2 = 15
x3 = 12, y3 = 17
x = 11
Using Lagrange’s formula,