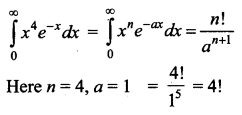Students can download 12th Business Maths Chapter 2 Integral Calculus I Ex 2.12 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.12
Choose the correct answer.
Question 1.

Answer:
(b) \(\frac{-1}{2 x^{2}}+c\)
Hint:
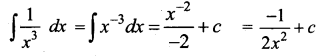
Question 2.

Answer:
(c) \(\frac{2^{x}}{\log 2}+c\)
Question 3.
\(\int \frac{\sin 2 x}{2 \sin x} d x\) is _______
(a) sin x + c
(b) \(\frac {1}{2}\) sin x + c
(c) cos x + c
(d) \(\frac {1}{2}\) cos x + c
Answer:
(a) sin x + c
Hint:
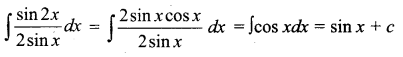
Question 4.
\(\int \frac{\sin 5 x-\sin x}{\cos 3 x} d x\) is _____
(a) -cos 2x + c
(b) –\(\frac {1}{2}\) cos 2x + c
(c) \(-\frac{1}{4}\) cos 2x + c
(d) -4 cos 2x + c
Answer:
(a) -cos 2x + c
Hint:
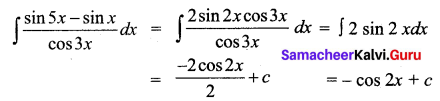
Question 5.

Answer:
(a) \(\frac{1}{2}(\log x)^{2}\)
Hint:
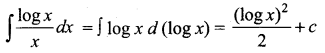
Question 6.
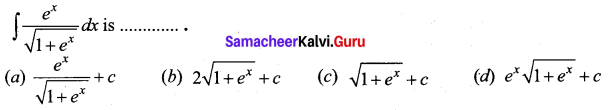
Answer:
(b) \(2 \sqrt{1+e^{x}}+c\)
Hint:
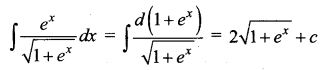
Question 7.

Answer:
(b) \(2 \sqrt{e^{x}}+c\)
Hint:
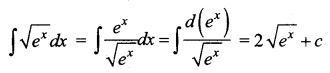
Question 8.

Answer:
(a) \(e^{2 x} x^{2}+c\)
Hint:
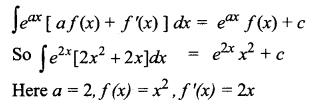
Question 9.

Answer:
(d) \(\log \left|e^{x}+1\right|+c\)
Hint:
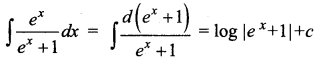
Question 10.
\(\int\left[\frac{9}{x-3}-\frac{1}{x+1}\right] d x\) is _____
(a) log|x – 3| – log|x + 1| + c
(b) log|x – 3| + log|x + 1| + c
(c) 9log|x – 3| – log|x + 1| + c
(d) 91og|x – 3| + log|x + 1| + c
Answer:
(c) 9log|x – 3| – log|x + 1| + c
Question 11.

Answer:
(b) \(\frac{1}{2} \log \left|4+x^{4}\right|+c\)
Hint:
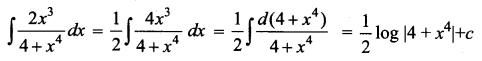
Question 12.

Answer:
(b) \(\log |x+\sqrt{x^{2}-36}|+c\)
Hint:
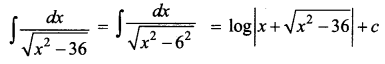
Question 13.

Answer:
(b) \(2 \sqrt{x^{2}+3 x+2}+c\)
Hint:
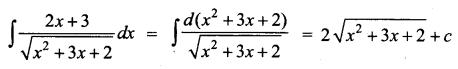
Question 14.
\(\int_{0}^{1}(2 x+1) d x\) is _______
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2
Hint:
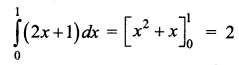
Question 15.
\(\int_{2}^{4} \frac{d x}{x}\) is _______
(a) log 4
(b) 0
(c) log 2
(d) log 8
Answer:
(c) log 2
Hint:
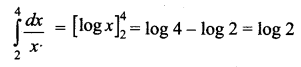
Question 16.
\(\int_{0}^{\infty} e^{-2 x} d x\) is _____
(a) 0
(b) 1
(c) 2
(d) \(\frac{1}{2}\)
Answer:
(d) \(\frac{1}{2}\)
Hint:
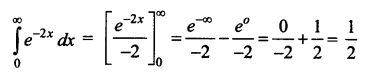
Question 17.
\(\int_{-1}^{1} x^{3} e^{x^{4}} d x\) is _______
(a) 1
(b) \(2 \int_{0}^{1} x^{3} e^{x^{4}} d x\)
(c) 0
(d) 2
Answer:
(c) 0
Hint:

Question 18.
If f(x) is a continous function and a < c < b, then \(\int_{a}^{c} f(x) d x+\int_{c}^{b} f(x) d x\) is _____
(a) \(\int_{a}^{b} f(x) d x-\int_{a}^{c} f(x) d x\)
(b) \(\int_{a}^{c} f(x) d x-\int_{a}^{a} f(x) d x\)
(c) \(\int_{a}^{b} f(x) d x\)
(d) 0
Answer:
(c) \(\int_{a}^{b} f(x) d x\)
Question 19.
The value of \(\int_{\frac{\pi}{2}}^{\frac{\pi}{2}} \cos x d x\) is _______
(a) 0
(b) 2
(c) 1
(d) 4
Answer:
(b) 2
Hint:

Question 20.
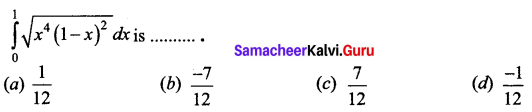
Answer:
(a) \(\frac{1}{12}\)
Hint:
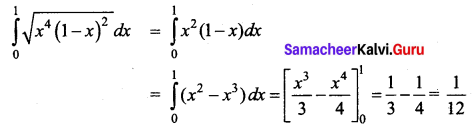
Question 21.
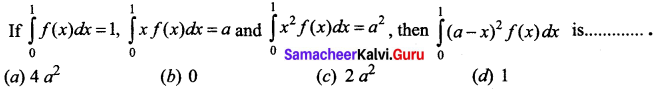
Answer:
(b) 0
Hint:
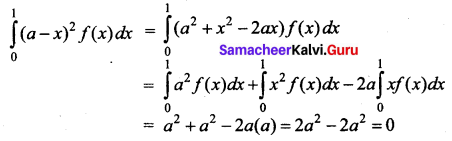
Question 22.
The value of \(\int_{2}^{3} f(5-x) d x-\int_{2}^{3} f(x) d x\) is _______
(a) 1
(b) 0
(c) -1
(d) 5
Answer:
(b) 0
Hint:

Question 23.

Answer:
(c) \(\frac{28}{3}\)
Hint:
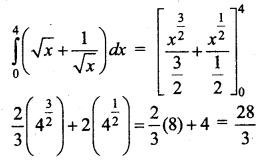
Question 24.
\(\int_{0}^{\frac{\pi}{3}} \tan x d x\) is _______
(a) log 2
(b) 0
(c) log√2
(d) 2 log 2
Answer:
(a) log 2
Hint:
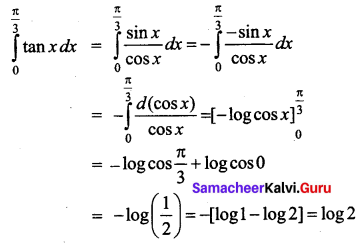
Question 25.
Using the factorial representation of the gamma function, which of the following is the solution for the gamma function Γ(n) when n = 8 is _______
(a) 5040
(b) 5400
(c) 4500
(d) 5540
Answer:
(a) 5040
Hint:
Γ(8) = Γ(7 + 1) = 7! = 5040
Question 26.
Γ(n) is _____
(a) (n – 1)!
(b) n!
(c) n Γ(n)
(d) (n – 1) Γ(n)
Answer:
(a) (n – 1)!
Hint:
Γ(n) = Γ(n – 1) + 1 = (n – 1)!
Question 27.
Γ(1) is ______
(a) 0
(b) 1
(c) n
(d) n!
Answer:
(b) 1
Hint:
Γ(1) = (1 – 1)! = 0! = 1
Question 28.

Answer:
(d) \(\int_{0}^{\infty} e^{-x} x^{n-1} d x\)
Question 29.
Γ(\(\frac{3}{2}\)) is _____
(a) √π
(b) \(\frac{\sqrt{\pi}}{2}\)
(c) 2√π
(d) \(\frac{3}{2}\)
Answer:
(b) \(\frac{\sqrt{\pi}}{2}\)
Hint:
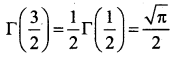
Question 30.
\(\int_{0}^{\infty} x^{4} e^{-x} d x\) is _______
(a) 12
(b) 4
(c) 4!
(d) 64
Answer:
(c) 4!
Hint: