Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.1

Students can download 12th Business Maths Chapter 4 Differential Equations Ex 4.1 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.1

Question 1.
Find the order and degree of the following differential equations.

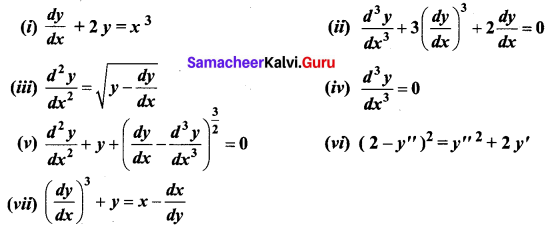
Solution:

Question 2.
Find the differential equation of the following
(i) y = cx + c – c³
(ii) y = c(x – c)²
(iii) xy = c²
(iv) x² + y² = a²
Solution:
(i) y = cx + c – c³ ……… (1)
Differentiating w.r.t. x, we get
\(\frac { dy }{dx}\) = c(1) + 0 ⇒ c = \(\frac { dy }{dx}\)
Equation (1) ⇒ y = x(\(\frac { dy }{dx}\)) + (\(\frac { dy }{dx}\)) – (\(\frac { dy }{dx}\))³

(ii) y = c(x – c)² …… (1)
We have to eliminate c
Differentiating w.r.t x ,we get, \(\frac{d y}{d x}\) = 2c(x – c) ….. (2)
Dividing (2) by (1) we get

Question 3.
Form the differential equation by eliminating α and β from (x – α)² + (y – β)² = r²
Solution:

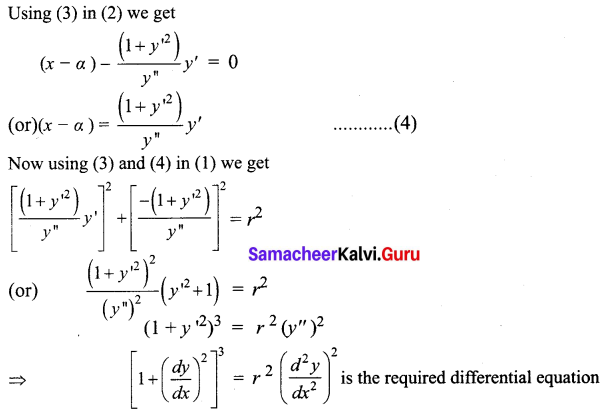
Question 4.
Find the differential equation of the family of all straight lines passing through the origin.
Solution:
Equation of the straight line passing through the origin (0, 0) is y = mx ………. (1)
Differentiating w.r. to x, we get
\(\frac { dy }{dx}\) = m(1) ⇒ m = \(\frac { dy }{dx}\)
Substituting this value of m in equation (1)
y = x\(\frac { dy }{dx}\)

Question 5.
Form the differential equation that represents all parabolas each of which has a latus rectum 4a and whose axes are parallel to the x-axis.
Solution:
Equation of parabola whose axis is parallel to the x-axis with latus rectum 4a is
(y – β)² = 4a(x – α) ………(1)
Here (α, β) is the vertex of the parabola.
Differentiating (1) w.r.t x, we get
2(y – β) \(\frac{d y}{d x}\) = 4a ……. (2)
Again, differentiating (2) w.r.t x, we get

Question 6.
Find the differential equation of all circles passing through the origin and having their centers on the y-axis.
Solution:

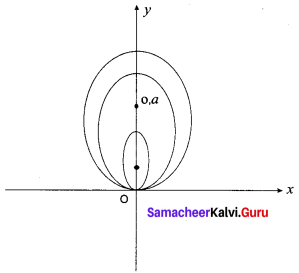
The circles pass through the origin. They have their centres at (o, a)
The circles have radius a. so the equation of the family of circles is given by
x² + (y – a)² = a²
x² + y² – 2ay + a² = a²
x² + y² = 2ay ……. (1)
Differentiating w.r.t x,

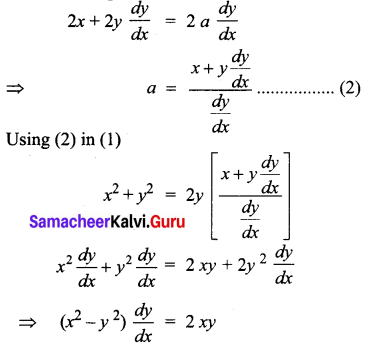
\(\frac{d y}{d x}=\frac{2 x y}{x^{2}-y^{2}}\) is the required differential equation of all circles passing through origin and having their centres on the y-axis.

Question 7.
Find the differential equation of the family of a parabola with foci at the origin and axis along the x-axis.
Solution:
The given family of parabolas have foci at the origin and axis along the x-axis.

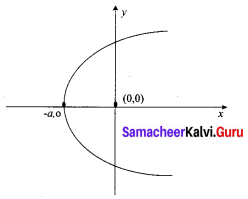
The equation of such family of parabolas is given by
y² = 4a(x + a) …… (1)
Differentiating w.r.t x,

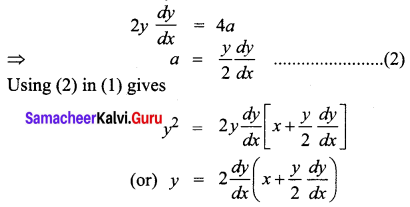
\(y=2 x \frac{d y}{d x}+y\left(\frac{d y}{d x}\right)^{2}\) is the required differential equation.