Students can download 12th Business Maths Chapter 4 Differential Equations Ex 4.6 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.6
Choose the correct answer.
Question 1.
The degree of the differential equation \(\frac{d^{4} y}{d x^{4}}-\left(\frac{d^{2} y}{d x^{2}}\right)^{4}+\frac{d y}{d x}=3\) is _________
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(a) 1
Hint:
Highest order derivative is \(\frac { d^2y }{dx^4}\)
Power of the highest order derivative is 1
∴ degree = 1
Question 2.
The order and degree of the differential equation \(\sqrt{\frac{d^{2} y}{d x^{2}}}=\sqrt{\frac{d y}{d x}+5}\) are respectively
(a) 2 and 3
(b) 3 and 2
(c) 2 and 1
(d) 2 and 2
Answer:
(c) 2 and 1
Hint:
Squaring both sides, we get \(\frac{d^{2} y}{d x^{2}}=\frac{d y}{d x}+5\)
So order = 2, degree = 1
Question 3.
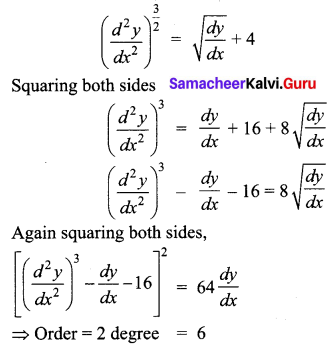
The order and degree of the differential equation \(\left(\frac{d^{2} y}{d x^{2}}\right)^{\frac{3}{2}}-\sqrt{\left(\frac{d y}{d x}\right)}-4=0\) are respectively.
(a) 2 and 6
(b) 3 and 6
(c) 1 and 4
(d) 2 and 4
Answer:
(a) 2 and 6
Hint:
Question 4.
The differential equation \(\left(\frac{d x}{d y}\right)^{3}+2 y^{\frac{1}{2}}=x\) is _________
(a) of order 2 and degree 1
(b) of order 1 and degree 3
(c) of order 1 and degree 6
(d) of order 1 and degree 2
Answer:
(b) of order 1 and degree 3
Question 5.
The differential equation formed by eliminating a and b from y = aex + be-x is _______
(a) \(\frac{d^{2} y}{d x^{2}}-y=0\)
(b) \(\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}=0\)
(c) \(\frac{d^{2} y}{d x^{2}}=0\)
(d) \(\frac{d^{2} y}{d x^{2}}-x=0\)
Answer:
(a) \(\frac{d^{2} y}{d x^{2}}-y=0\)
Hint:
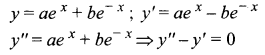
Question 6.
If y = cx + c – c3 then its differential equation is ______

Answer:
(a) \(y=x \frac{d y}{d x}+\frac{d y}{d x}-\left(\frac{d y}{d x}\right)^{3}\)
Hint:
y = cx + c – c³ ……… (1)
\(\frac { dy }{dx}\) = c
(1) ⇒ y = x\(\frac { dy }{dx}\) + \(\frac { dy }{dx}\) – (\(\frac { dy }{dx}\))³
Question 7.
The integrating factor of the differential equation \(\frac{d x}{d y}\) + Px = Q is _____
(a) e∫Pdx
(b) ∫Pdx
(c) ∫Pdy
(d) e∫Pdy
Answer:
(d) e∫Pdy
Question 8.
The complementary function of (D2 + 4) y = e2x is _______
(a) (Ax + B) e2x
(b) (Ax + B) e-2x
(c) A cos 2x + B sin 2x
(d) Ax-2x + Be2x
Answer:
(c) A cos 2x + B sin 2x
Hint:
(D² + 4) y = e2x
The auxiliary equation is m² + 4 = 0
m² = -4 ⇒ m = ±\(\sqrt { -4}\)
m = ± 2i
It is of the form α ± ß i
Here α = 0 and ß = 2
C.F = eαx (A cos ßx + B sin ßx)
= e° (A cos2x + B sin2x)
C.F = A cos2x + B sin2x
Question 9.
The differential equation of y = mx + c is (m and c are arbitrary constants).
(a) \(\frac{d^{2} y}{d x^{2}}=0\)
(b) y = x \(\frac{d y}{d x}\)
(c) x dy + y dx = 0
(d) y dx – x dy = 0
Answer:
(a) \(\frac{d^{2} y}{d x^{2}}=0\)
Hint:
y = mx + c
\(\frac { dy }{dx}\) = m ⇒ \(\frac { d^2y }{dx^2}\) = 0
Question 10.
The particular integral of the differential equation \(\frac{d^{2} y}{d x^{2}}-8 \frac{d y}{d x}+16 y=2 e^{4 x}\) is ________
(a) \(\frac{x^{2} e^{4 x}}{2 !}\)
(b) \(\frac{e^{4 x}}{2 !}\)
(c) x2 e4x
(d) xe4x
Answer:
(c) x2 e4x
Hint:

Question 11.
Solution of \(\frac{d x}{d y}\) + px = 0
(a) x = cepy
(b) x = ce-py
(c) x = py + c
(d) x = cy
Answer:
(b) x = ce-py
Hint:
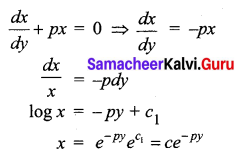
Question 12.
If sec2 x is an integrating factor of the differential equation \(\frac{d y}{d x}\) + Py = Q then P = _____
(a) 2 tan x
(b) sec x
(c) cos2 x
(d) tan2 x
Answer:
(a) 2 tan x
Hint:
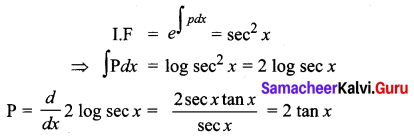
Question 13.
The integrating factor of x\(\frac{d y}{d x}\) – y = x2 is _____
(a) \(\frac{-1}{x}\)
(b) \(\frac{1}{x}\)
(c) log x
(d) x
Answer:
(b) \(\frac{1}{x}\)
Hint:
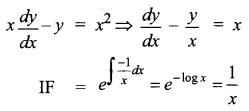
Question 14.
The solution of the differential equation \(\frac{d y}{d x}\) + Py = Q where P and Q are the function of x is ______

Answer:
(c) \(y e^{\int p d x}=\int \mathrm{Q} e^{\int p d x} d x+c\)
Question 15.
The differential equation formed by eliminating A and B from y = e-2x (A cos x + B sin x) is _______
(a) y2 – 4y1 + 5y = 0
(b) y2 + 4y1 – 5y = 0
(c) y2 – 4y1 – 5y = 0
(d) y2 + 4y1 + 5y = 0
Answer:
(d) y2 + 4y1 + 5y = 0
Hint:

Question 16.
The particular integral of the differential equation f(D) y = eax where f(D) = (D – a)2 ________
(a) \(\frac{x^{2}}{2} e^{2 x}\)
(b) xeax
(c) \(\frac{x}{2} e^{2 x}\)
(d) x2 e2x
Answer:
(a) \(\frac{x^{2}}{2} e^{2 x}\)
Question 17.
The differential equation of x2 + y2 = a2 is _____
(a) x dy + y dx = 0
(b) y dx – x dy = 0
(c) x dx – y dx = 0
(d) x dx + y dy = 0
Answer:
(d) x dx + y dy = 0
Hint:
x² + y² = a²
Differentiating w.r.t x
2x+ 2y\(\frac { dy }{dx}\) = 0
2x = -2y \(\frac { dy }{dx}\) ⇒ x = -y\(\frac { dy }{dx}\)
xdx = -ydy ⇒ xdx + ydy = 0
Question 18.
The complementary function of \(\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}=0\) is ______
(a) A + B ex
(b) (A + B) ex
(c) (Ax + B) ex
(d) (Aex + B)
Answer:
(a) A + B ex
Hint:
\(\frac { d^y }{dx^2}\) – \(\frac { dy }{dx}\) = 0
The auxiliary equation is m² – m = 0
m(m – 1) = 0 ⇒ m = 0, 1.
The roots are real and different
∴ C.F = Aem1x + Bem2x
C.F = Ae0x + Be1x
= A + Bex
Question 19.
The P.I of (3D2 + D – 14)y = 13e2x is _______
(a) \(\frac{x}{2}\) e2x
(b) x e2x
(c) \(\frac{x^{2}}{2}\) e2x
(d) 13xe2x
Answer:
(b) xe2x
Hint:

Question 20.
The general solution of the differential equation \(\frac{d y}{d x}\) = cos x is _______
(a) y = sin x + 1
(b) y = sin x – 2
(c) y = cos x + c, c is an arbitrary constant
(d) y = sin x + c, c is an arbitrary constant
Answer:
(d) y = sin x + c, c is an arbitrary constant
Hint:
\(\frac { dy }{dx}\) = cos x
dy = cos x dx
∫dy = ∫cos x dx ⇒ y = sin x + c
Question 21.
A homogeneous differential equation of the form \(\frac{d y}{d x}=f\left(\frac{y}{x}\right)\) can be solved by making substitution
(a) y = vx
(b) v = yx
(c) x = vy
(d) x = v
Answer:
(a) y = vx
Question 22.
A homogeneous differential equation of the form \(\frac{d x}{d y}=f\left(\frac{x}{y}\right)\) can be solved by making substitution,
(a) x = vy
(b) y = vx
(c) y = v
(d) x = v
Answer:
(a) x = vy
Question 23.
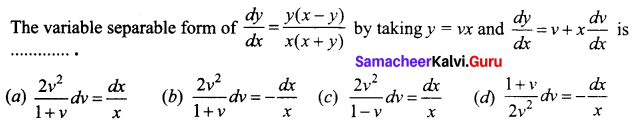
Answer:
(d) \(\frac{1+v}{2 v^{2}} d v=-\frac{d x}{x}\)
Hint:
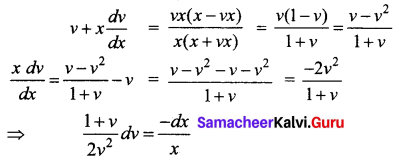
Question 24.
Which of the following is the homogeneous differential equation?
(a) (3x – 5) dx = (4y – 1) dy
(b) xy dx – (x3 + y3) dy = 0
(c) y2 dx + (x2 – xy – y2) dy = 0
(d) (x2 + y) dx = (y2 + x) dy
Answer:
(c) y2 dx + (x2 – xy – y2) dy = 0
Question 25.
The solution of the differential equation \(\frac{d y}{d x}=\frac{y}{x}+\frac{f\left(\frac{y}{x}\right)}{f^{\prime}\left(\frac{y}{x}\right)}\) is ______
(a) f(\(\frac{y}{x}\)) = kx
(b) x f(\(\frac{y}{x}\)) = k
(c) f(\(\frac{y}{x}\)) = ky
(d) y f(\(\frac{y}{x}\)) = k
Answer:
(a) f(\(\frac{y}{x}\)) = kx
Hint:
