Students can Download Maths Chapter 2 Life Mathematics Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 3 Chapter 2 Life Mathematics Intext Questions
Exercise 2.1
Try These (Text book Page No. 33)
Classify the given examples as direct or inverse proportion:
(i) Weight of pulses to their cost.
Solution:
As weight increases cost also increases.
∴ Weight and cost are direct proportion.
(ii) Distance travelled by bus to the price of ticket.
Solution:
As the distance increases price to travel also increases.
∴ Distance and price are direct proportion.
(iii) Speed of the athelete to cover a certain distance.
Solution:
As the speed increases, the time to cover the distance become less.
So speed and time are in indirect proportion.
(iv) Number of workers employed to complete a construction in a specified time.
Solution:
As the number of workers increases, the amount of work become less, so they are in indirect proportion.
(v) Volume of water flown through a pipe to its pressure.
Solution:
As the pressure increases, volume also increases.
∴ They are direct proportions.
(vi) Area of a circle to its radius.
Solution:
If the radius of the circle increases its area also increases.
∴ Area and radius of circles are direct proportion.
![]()
Use the concept of direct and inverse proportions and try to answer the following questions:
Question 1.
A student can type 21 pages in 15 minutes. At the same rate, how long will it take the student to type 84 pages?
Solution:
Direct proportion
No. of minutes = x
k = \(\frac{21}{15}\)
\(\frac{21}{15}\) = \(\frac{84}{x}\)

Question 2.
The weight of an iron pipe varies directly with its length. If 8 feet of an iron pipe weighs 3.2 kg, find the proportionality constant k and determine the weight of a 36 feet iron pipe.
Solution:

Weight of 36 feet iron pipe = x
\(\frac{36}{x}\) = 2.5
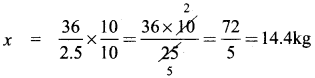
Question 3.
A car covers a distance of 765 km in 51 litres of petrol. How much distance would it cover in 30 litres of petrol?
Solution:
Direct proportion
k = \(\frac{51}{765}\)
Distance cover = x km
\(\frac{30}{x}\) = \(\frac{51}{765}\)
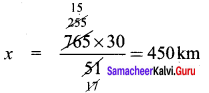
Question 4.
If x and y vary inversely and x = 24 when y = 8, find x when y = 12.
Solution:
k = xy = 24 × 8 = 192
∴ 12 × x = 192

Question 5.
If 35 women can do a piece of work in 16 days, in how many days will 28 women do the same work?
Solution:
Inverse proportion
No. of days = x
k = 35 × 16
∴ 28 × x = 35 × 16
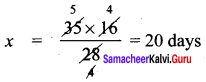
Question 6.
A farmer has food for 14 cows which can last for 39 days. How long would the food last, if 7 more cows join his cattle?
Solution:
Inverse variation
k = xy = 14 × 39
No. of cow = 14 + 7 = 21
No. of days = x
21 × x = 14 × 39
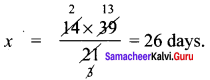
![]()
Question 7.
Identify the type of proportion and fill in the blank boxes:

Solution:
Direct proportion
\(\frac{x}{y}\) = k = \(\frac{1}{20}\)
(i) x = 2; y = ?
\(\frac{2}{y}\) = \(\frac{1}{20}\) ⇒ y = 2 × 20 = 40
(ii) x = ?; y = 60
\(\frac{x}{60}\) = \(\frac{1}{20}\) ⇒ x = \(\frac{60}{20}\) = 3
(iii) x = 4; y = ?
\(\frac{4}{y}\) = \(\frac{1}{20}\) ⇒ y = 80
(iv) x = 4; y = ?
\(\frac{8}{y}\) = \(\frac{1}{20}\) ⇒ y = 20 × 8 = 160
(v) x = ?; y = 180
\(\frac{x}{180}\) = \(\frac{1}{20}\)
x = \(\frac{180}{20}\) = 9
(vi) x = 12; y = ?
\(\frac{12}{y}\) = \(\frac{1}{20}\)
y = 12 × 20 = 240
(vii) x = ?; y = 360
\(\frac{x}{360}\) = \(\frac{1}{20}\) ⇒ x = \(\frac{360}{20}\) = 18
(viii) x = 24; y = ?
\(\frac{24}{y}\) = \(\frac{1}{20}\) ⇒ y = 24 × 20 = 480
Question 8.
Identify the type of proportion and fill in the blank boxes:

Solution:
Inverse proportion
k = xy = 1 × 144 = 144
(i) x = 2; y = ?
2y = 144
y = 72
(ii) X = ?; y = 48
48x = 144
x = \(\frac{144}{48}\) = 3
(iii) x = 4; y = ?
4y = 144
y = \(\frac{144}{4}\) = 36
(iv) x = 8; y = ?
8 y = 144
y = \(\frac{144}{8}\) = 18
(v) x = ?; y = 16
16x = 144
y = \(\frac{144}{16}\) = 9
(vi) x = 12; y = ?
12y = 144
y = \(\frac{144}{12}\) = 12
(vii) x = ?; y = 9
9x = 144
x = \(\frac{144}{9}\) = 16
(viii) x = 24; y = ?
24y = 144
y = \(\frac{144}{24}\) = 6
![]()
Try These (Text book Page No. 38)
Question 1.
When x = 5 and y = 5 find k, if x and y vary directly.
Solution:
If x and y vary directly then \(\frac{x}{y}\) = k
Here x = 5; y = 5
∴ k = \(\frac{5}{5}\)
k = 1
Question 2.
When x and y vary inversely, find the constant of variation when x = 64 and y = 0.75
Solution:
Given
x =64, y = 0.75
and also given x and y vary inversely.
∴ xy = k. the constant of variation.
∴ Constant = 64 × 0.75
Constant of variation = 48
Think (Text book Page No. 38)
(i) When x and y are in direct proportion and if y is doubled, then what happens to x?
Solution:
If x and y are in direct proportion \(\frac{x}{y}\) = k, constant.
if y is doubled, then \(\frac{x}{2}\) must be equal to k. So x also to be doubled.
(ii) if \(\frac{x}{y-x}\) = \(\frac{6}{7}\) What is \(\frac{x}{y}\)?
Solution:
if \(\frac{x}{y-x}\) = \(\frac{6}{7}\)
\(\frac{y-x}{x}\) = \(\frac{7}{6}\)
\(\frac{y}{x}\) – \(\frac{x}{x}\) = \(\frac{7}{6}\)
\(\frac{y}{x}\) = \(\frac{7}{6}\) + \(\frac{x}{x}\)
\(\frac{y}{x}\) = \(\frac{7}{6}\) + 1
\(\frac{y}{x}\) = \(\frac{7+6}{6}\)
\(\frac{y}{x}\) = \(\frac{13}{6}\)
\(\frac{x}{y}\) = \(\frac{6}{13}\)
Try These (Text book Page No. 40)
Identify the different variations present in the following questions:
Question 1.
24 men can make 48 articles in 12 days. Then, 6 men can make …………. articles in 6 days.
Solution:
Let the required no. of articles be x
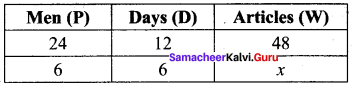
(i) Mens and days are Indirect variables.
(ii) Men and Articles are direct variables
(iii) Days and articles are also direct variables using formula.
Let P1 = 24, D1 = 12, W1 = 48
P2 = 6, D2 = 6, W2 = x
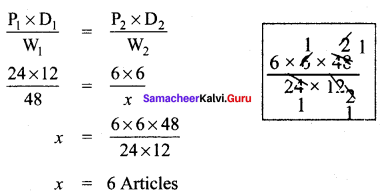
Question 2.
15 workers can lay a road of length 4 km In 4 hours. Then, …………. workers can lay a road of length 8 km in 8 hours.
Solution:
Let the required number of workers be x

Length and workers are direct variable as more length need more workers.
The proportion is 4 : 8 : : 15 : x ……….(1)
Hours and workers are indirect variables as more working hours need less men.
∴ The proportion is 8 : 4 : : 15 : x ………..(2)
Combining (1) and (2)
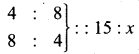
Product of the extremes = product of the means
4 × 8 × x = 8 × 4 × 15
x = \(\frac{8×4×15}{4×8}\)
x = 15 workers
![]()
Question 3.
25 women working 12 hours a day can complete a work in 36 days. Then, 20 women must ……….. work hours to complete the same work in 30 days.
Solution:
Let the required hours be x

As women increases hours to work decreases
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{25}{20}\)
As days increases hours needed become less
∴ It is also an indirect variation.
∴ Multiplying factor is \(\frac{36}{30}\)
∴ x = 12 × \(\frac{25}{20}\) × \(\frac{36}{30}\)
x = 18 hours
Question 4.
In a camp, there are 420 kg of rice sufficient for 98 persons for 45 days. The number of days that 60 kg of rice will last for 42 persons is…………
Solution:
Let the required number of days be x.

If amount of rice is more it will last for more days.
∴ It is Direct Proportion.
∴ Multiplying factor is \(\frac{60}{420}\)
If men increases number of days the rice lasts decreases
∴ It is an inverse proportion.
∴ Multiplying factor is \(\frac{98}{42}\)
x = 45 × \(\frac{60}{420}\) × \(\frac{98}{42}\)

x = 15 days
Try These (Text book Page No. 44)
Question 1.
Vikram can do one-third of work in p days. He can do \(\frac{3}{4}\)th of work in ………… days.
Solution:
\(\frac{1}{3}\) of the work will be done in p days
∴ Full work will be completed in 3p days
\(\frac{3}{4}\)th of the work will be done in = 3p × \(\frac{3}{4}\) = \(\frac{9}{4}\)p = 2\(\frac{1}{4}\)p days
![]()
Question 2.
If m persons can complete a work in n days, then 4m persons can complete the same work in ……….. days and \(\frac{m}{4}\) persons can complete the same work in…….. days
Solution:
Given m persons complete a work in n days
(i) Then work measured in terms of Man days = mn
4 m men do the work it will be completed in \(\frac{mn}{4m}\) days = \(\frac{n}{4}\) days.
(ii) \(\frac{m}{4}\) persons can complete the same work in \(\frac{mn}{\frac{m}{4}}\) days = \(\frac{4mn}{m}\) = 4n days