Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 3 Algebra Intext Questions

Students can Download Maths Chapter 3 Algebra Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 3 Chapter 3 Algebra Intext Questions

Exercise 3.1
Think (Text book Page No. 50)

Question 1.
Is it the only way to decompose the numbers representing length and breadth? Discuss.
Solution:
No, for example 15 can be decompose into 1 × 15, 3 × 5, 5 × 3, 15 × 1

Try These (Text book Page No. 52)

Question 1.
Observe the following figures and try to find its area, geometrically. Also verify the same by multiplication of monomial.

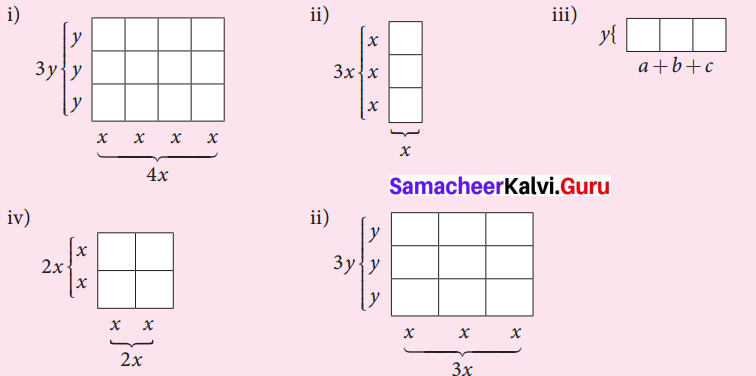
Solution:
Area of each box = xy
Totally 12 boxes
∴ Total area = 12 × xy = 12xy
Also multiplying the length 4x and breadth 3y
We have area of the rectangle = 4x × 3y = 12xy

(ii) Area of each small box = x²
Total number of boxes = 3
∴ Total area = 3x²
Also length of the rectangle = 3x
breadth of the rectangle = x
Area of the rectangle = length × breadth
= 3x × x
= 3x²

(iii) Area of each small box is ay, by, cy
∴ Total area = ay + by + cy = y (a + b + c)
Area of the rectangle = length × breadth
= (a + b + c) y

(iv) Area of each small square = x²
There are 4 small squares
∴ Total area of the given square = 4x²
Also side of the big square = 2x
∴ Area of the square = (2x)² = 4x²

(v) Area of each small rectangle = xy
There are 9 such rectangles
∴ Total area = 9xy
Area of big rectangle = lenght × breath
= 3x × 3y = 9xy

Question 2.
Let the length and breadth of a tile be x and y respectively. Using such tiles construct as many rectangles as you can and find out the length and breadth of the rectangles so formed such that its area is
(i) 12 xy
(ii) 8xy
(iii) 9xy
Solution:

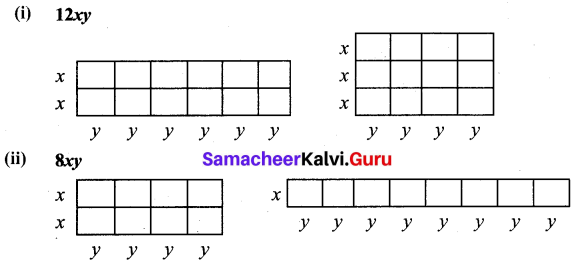
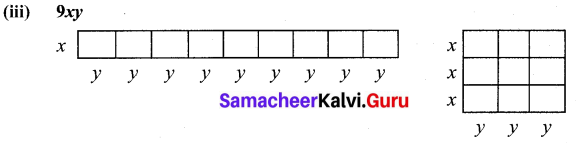
Try These (Text book Page No. 58)

Question 1.
Consider a square shaped paddy field with side of 48 m. A pathway with uniform breadth is surrounded the square field and the length of the outer side is 52 m. Can you find the area of the pathway by using identities?
Solution:
Let a = 52
b = 4

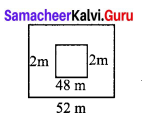
(a – b)² = a² – 2ab + b² = 52² – 2 (52) (4) + 4²
= 2704 – 416 + 16 = 2304

Think (Text book Page No. 60)

Question 1.
Can we factorize the following expressions using any basic identities? Justify your answer.
(i) x² + 5x + 4
(ii) x² – 5x + 4
Solution:
(i) x² + 5x + 4 = x2 + (1 + 4)x + (1 × 4)
Which is of the form x² + (a + b) x + ab
= (x + a) (x + b)
x² + (1 + 4)x + (1 × 4) = (x + 1) (x + 4)
∴ x² + 5x + 4 = (x + 1) (x + 4)

(ii) x² – 5x + 4 = x² + ((-1) + (- 4))x + (-1) (- 4)
Which is of the form x² + (a + b) x + ab
= (x + a) (x + b)
x² + ((-1) + 4))x + ((-1)(-4)) = (x + (-4)) = (x – 1) (x – 4)
x² – 5x + 4 = (x – 1) (x – 4))

Exercise 3.2
Try These (Text book Page No. 63)

Question 1.
Construct inequations for the following statements:
1. Ramesh’s salary is more than ₹ 25,000 per month.
2. This lift can carry maximum of 5 persons.
3. The exhibition will be there in town for at least 100 days.
Solution:
1. x > 25,000, where x is Ramesh’s Salary per month.
2. y < 5, where y is the maximum number of persons the left can carry.
3. z > 100, where z is the number of days when the exhibition is there.

Think (Text book Page No. 65)

Question 1.
Hameed saw a stranger in the street. He told his parent, “The stranger’s age is between 40 to 45 years, and his height is between 160 to 170 cm”
Convert the above verbal statement into algebraic inequations by using x and y as variables of age and height.
Solution:
Let x be the age and y be the height then
40 < x < 45 and 160 < y < 170