Students can Download Physics Chapter 2 Current Electricity Questions and Answers, Notes Pdf, Samacheer Kalvi 12th Physics Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Physics Solutions Chapter 2 Current Electricity
Samacheer Kalvi 12th Physics Current Electricity Textual Evaluation Solved
Samacheer Kalvi 12th Physics Current Electricity Multiple Choice Questions
Question 1.
The following graph shows current versus voltage values of some unknown conductor. What is the resistance of this conductor?
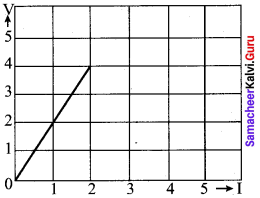
(a) 2 ohm
(b) 4 ohm
(c) 8 ohm
(d) 1 ohm
Answer:
(a) 2 ohm
Question 2.
A wire of resistance 2 ohms per meter is bent to form a circle of radius 1 m. The equivalent resistance between its two diametrically opposite points, A and B as shown in the figure is-
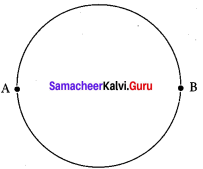
(a) π Ω
(b) \(\frac { π }{ 2 }\) Ω
(c) 2π Ω
(d) \(\frac { π }{ 4 }\) Ω
Answer:
(b) \(\frac { π }{ 2 }\) Ω
![]()
Question 3.
A toaster operating at 240 V has a resistance of 120 Ω. The power is
(a) 400 W
(b) 2 W
(c) 480 W
(d) 240 W
Answer:
(c) 480 W
Question 4.
A carbon resistor of (47 ± 4.7) k Ω to be marked with rings of different colours for its identification. The colour code sequence will be
(a) Yellow – Green – Violet – Gold
(b) Yellow – Violet – Orange – Silver
(c) Violet – Yellow – Orange – Silver
(d) Green – Orange – Violet – Gold
Answer:
(b) Yellow – Violet – Orange – Silver
Question 5.
What is the value of resistance of the following resistor?

(a) 100 k Ω
(b) 10 k Ω M
(c) 1 k Ω
(d) 1000 k Ω
Answer:
(a) 100 k Ω
Question 6.
Two wires of A and B with circular cross section made up of the same material with equal lengths. Suppose RA = 3 RB, then what is the ratio of radius of wire A to that of B?
(a) 3
(b) √3
(c) \(\frac { 1 }{ √3 }\)
(d) \(\frac { 1 }{ 3 }\)
Answer:
(c) \(\frac { 1 }{ √3 }\)
Question 7.
A wire connected to a power supply of 230 V has power dissipation P1 Suppose the wire is cut into two equal pieces and connected parallel to the same power supply. In this case power dissipation is P2. The ratio \(\frac {{ p }_{2}}{{ p }_{1}}\) is.
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4
Question 8.
In India electricity is supplied for domestic use at 220 V. It is supplied at 110 V in USA. If the resistance of a 60W bulb for use in India is R, the resistance of a 60W bulb for use in USA will be
(a) R
(b) 2R
(c) \(\frac { R }{ 4 }\)
(d) \(\frac { R }{ 2 }\)
Answer:
(c) \(\frac { R }{ 4 }\)
Question 9.
In a large building, there are 15 bulbs of 40 W, 5 bulbs of 100 W, 5 fans of 80 W and 1 heater of 1kW are connected. The voltage of electric mains is 220 V. The minimum capacity of the main fuse of the building will be (IIT-JEE 2014)
(a) 14 A
(b) 8 A
(c) 10 A
(d) 12 A
Answer:
(d) 12 A
![]()
Question 10.
There is a current of 1.0 A in the circuit shown below. What is the resistance of P ?
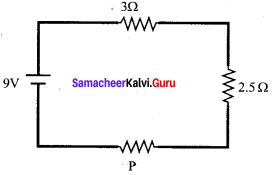
(a) 1.5 Ω
(b) 2.5 Ω
(c) 3.5 Ω
(d) 4.5 Ω
Answer:
(c) 3.5 Ω
Question 11.
What is the current out of the battery?
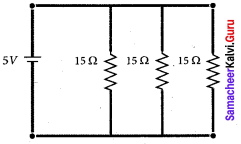
(а) 1 A
(b) 2 A
(c) 3 A
(d) 4 A
Answer:
(а) 1 A
Question 12.
The temperature coefficient of resistance of a wire is 0.00125 per °C. At 300 K, its resistance is 1 Ω. The resistance of the wire will be 2 Ω. at
(a) 1154 K
(ft) 1100 K
(c) 1400 K
(d) 1127 K
Answer:
(d) 1127 K
Question 13.
The internal resistance of a 2.1 V cell which gives a current of 0.2 A through a resistance of 10Ω is
(a) 0.2 Ω
(b) 0.5 Ω
(c) 0.8 Ω
(d) 1.0 Ω
Answer:
(b) 0.5 Ω
Question 14.
A piece of copper and another of germanium are cooled from room temperature to 80 K. The resistance of
(a) each of them increases
(b) each of them decreases
(c) copper increases and germanium decreases
(d) copper decreases and germanium increases
Answer:
(d) copper decreases and germanium increases
![]()
Question 15.
In Joule’s heating law, when I and t are constant, if the H is taken along the y axis and I2 along the x axis, the graph is
(a) straight line
(b) parabola
(c) circle
(d) ellipse
Answer:
(a) straight line
Samacheer Kalvi 12th Physics Current Electricity Short Answer Questions
Question 1.
Why current is a scalar?
Answer:
Although, a direction is associated with electric current, yet it is a scalar quantity. The reason is that the laws of ordinary algebra are used to add electric current. The laws of vector algebra do not apply to the addition of electric currents. In an electric circuit, the direction of current in the direction of conventional current.
Question 2.
Distinguish between drift velocity and mobility.
Answer:

Question 3.
State microscopic form of Ohm’s law.
Answer:
Current density J at a point in a conductor is the amount of current flowing per unit area of the conductor around that point provided the area is held in a direction normal to the current.
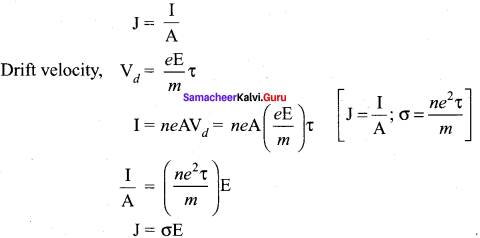
Question 4.
State macroscopic form of Ohm’s law.
Answer:
The microscopic form of Ohm’s law is
\(\vec{\jmath}=\frac{\mathrm{ne}^{2} \tau}{\mathrm{m}} \cdot \vec{E}\)
Where
τ → Current density
e → Charge of electron
\(\frac{\mathrm{e} \tau}{\mathrm{m}}\) → Drift velocity (vd)
E → applied electric field
Question 5.
What are ohmic and non-ohmic devices?
Answer:
Ohmic devices:
Devices where the current against voltage graph is a straight line through the origin and that obeys Ohm’s law is called ohmic devices.
Eg. conductors
Non-ohmic devices:
Devices where the VI graph is non-linear and that which do not obey ohm’s law is called Non-ohmic devices.
Eg. Diode
![]()
Question 6.
Define electrical resistivity.
Answer:
The electrical resistivity of a material is defined as the resistance offered to current flow by a conductor of unit length having a unit area of cross-section.
Question 7.
Define temperature coefficient of resistance.
Answer:
It is defined as the ratio of increase in resistivity per degree rise in temperature to its resistivity at T0
![]()
Question 8.
What is superconductivity?
Answer:
- It is defined as the ratio of increase in resistivity per degree rise in temperature to its resistivity at
\(\mathrm{T}_{\mathrm{o}} \cdot \alpha \pm=\frac{\Delta p}{\rho_{0} \Delta \mathrm{T}}\) - It is denoted as α and its unit is per °C.
Question 9.
What are electric power and electric energy?
Answer:
1. Electric power:
It is the rate at which an electric appliance converts electric energy into other forms of energy. Or, it is the rate at which work is done by a source of emf in maintaining an electric current through a circuit.
P = \(\frac { W }{ t }\) = VI = I2R = \(\frac {{ V }_{2}}{ R }\)
2. Electric energy:
It is the total work done in maintaining an electric current in an electric circuit for a given time.
W = Pt = VIt joule = I2Rt joule.
Question 10.
Define current density.
Answer:
The current density (J) is defined as the current per unit area of cross-section of the conductor
J = \(\frac { 1 }{ A }\)
The S.I unit of current density.
\(\frac { A }{{ m }^{2}}\)
Or
Am2
![]()
Question 11.
Derive the expression for power P = VI in electrical circuit.
Answer:
The electrical power P is the rate at which the electrical potential energy is delivered,
P = \(\frac { dU }{ dt }\) = \(\frac { d }{ dt }\) (V.dQ) = V\(\frac { dQ }{ dt }\)
Since the electric current I = \(\frac { dQ }{ dt }\)
So the equation can be rewritten as P = VI.
Question 12.
Write down the various forms of expression for power in electrical circuit.
Answer:
- Expression for electric power interms of I and R
P = VI, P = I2R (∴ V = IR) - Expression for electric power interms of V and R
P = VI, P = \(\frac{V^{2}}{R}\) (∴ I = \(\frac{\mathrm{V}}{\mathrm{R}}\))
Question 13.
State Kirchhoff’s current rule.
Answer:
It states that the algebraic sum of the currents at any junction of a circuit is zero. It is a statement of conservation of electric charge.
Question 14.
State Kirchhoff’s voltage rule.
Answer:
- Kirchhoff’s voltage rule states that in a closed circuit, the algebraic sum of the products of each part of the circuit is equal to the total emf included in the circuit.
i.e ΣClosed loop ΔV = 0 - It follows the law of conservation of energy.
Question 15.
State the principle of the potentiometer.
Answer:
The basic principle of a potentiometer is that when a constant current flows through a wire of uniform cross-sectional area and composition, the potential drop across any length of the wire is directly proportional to that length.
![]()
Question 16.
What do you mean by the internal resistance of a cell?
Answer:
During the process of flow of current inside the cell, resistance is offered the cell, resistance is offered to current flow by the electrolyte of the cell. This is termed the internal resistance of the cell.
Question 17.
State Joule’s law of heating.
Answer:
It states that the heat developed in an electrical circuit due to the flow of current varies directly as:
- the square of the current
- the resistance of the circuit and
- the time of flow.
H = I2R?
Question 18.
What is the Seebeck effect?
Answer:
In a closed circuit consisting of two dissimilar metals, an emf is developed when the junctions are maintained at different temperatures. This is called the Seebeck effect.
Question 19.
What is the Thomson effect?
Answer:
Thomson showed that if two points in a conductor are at different temperatures, the density of electrons at these points will differ and as a result, the potential difference is created between these points. Thomson effect is also reversible.
Question 20.
What is the Peltier effect?
Answer:
When an electric current is passed through a circuit of a thermocouple, heat is evolved at one Junction and absorbed at the other junction. This is known as the Peltier effect.
![]()
Question 21.
State the applications of the Seebeck effect.
Answer:
Applications of Seebeck effect:
- The Seebeck effect is used in thermoelectric generators. It is used in power plants to 2convert waste heat into electricity.
- It is used in automobiles as automotive thermoelectric generators for increasing fuel efficiency.
- It is used in thermocouples and thermopiles to measure the temperature difference between the two objects.
Samacheer Kalvi 12th Physics Current Electricity Long Answer Questions
Question 1.
Describe the microscopic model of current and obtain genera! form of Ohm’s Law.
Answer:
Microscopic model of current: Consider a conductor with area of cross-section A and an electric field E applied from right to left. Suppose there are n electrons per unit volume in the conductor and assume that all the electrons move with the same drift velocity \(\vec { v } \)d.
The drift velocity of the electrons = vd
The electrons move through a distance dx within a small interval of dt
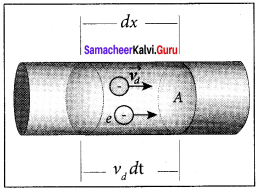
vd = \(\frac { dx }{ dt }\); dx = vddt ….. (1)
Since A is the area of cross section of the conductor, the electrons available in the volume or length dx is
= volume x number per unit volume
= A dx × n …… (2)
Substituting for dx from equation (1) in (2)
= (A vd dt)n
Total charge in volume element dQ = (charge) x (number of electrons in the volume element)
dQ= (e)(A vd dt)n
Hence the current, I = \(\frac { dQ }{ dt }\) = \(\frac{n e A v_{d} d t}{d t}\)
I = ne A vd …….. (3)
Current denshy (J):
The current density (J) is defined as the current per unit area of cross section of the conductor
J = \(\frac { I }{ A }\)
The S.I. unit of current density,\(\frac { A }{{ m }^{2}}\) (or) Am-2
J = \(\frac {{ neA v }_{d}}{ A }\) (from equation 3)
J = nevd …….. (4)
The above expression is valid only when the direction of the current is perpendicular to the area A. In general, the current density is a vector quantity and it is given by
\(\vec { J } \) = ne\(\vec { v } \)d
Substituting i from equation \(\vec { v } \)d = \(\frac { -eτ }{ m }\) \(\vec { E } \)
\(\vec { J } \) = –\(\frac{n \cdot e^{2} \tau}{m}\)\(\vec { E } \) …… (5)
\(\vec { J } \) = -σ\(\vec { E } \)
But conventionally, we take the direction of (conventional) current density as the direction of electric field. So the above equation becomes
\(\vec { J } \) = σ\(\vec { E } \) …….. (6)
where σ = \(\frac{n \cdot e^{2} \tau}{m}\) is called conductivity.
Equation 6 is called a microscopic form of ohm’s law.
Question 2.
Obtain the macroscopic form of Ohm’s law from its microscopic form and discuss its limitation.
Answer:
Ohm’s law: Ohm’s law can be derived from the equation J = σE. Consider a segment of wire of length l and cross-sectional area A.
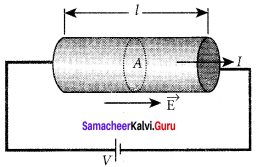
When a potential difference V is applied across the wire, a net electric field is created in the wire which constitutes the current. For simplicity, we assume that the electric field is uniform in the entire length of the wire, the potential difference (voltage V) can be written as V = El
As we know, the magnitude of current density
J = σE = σ\(\frac { V }{ l }\) ……. (1)
But J = \(\frac { I }{ A }\), so we write the equation as
\(\frac { I }{ A }\) σ\(\frac { V }{ l }\)
By rearranging the above equation, we get
V = I \(\left( \frac { l }{ \sigma A } \right) \) ……… (2)
The quantity \(\frac { l }{ \sigma A } \)is called resistance of the conductor and it is denoted as R. Note that the oA resistance is directly proportional to the length of the conductor and inversely proportional to area of cross section.
Therefore, the macroscopic form of Ohm’s law can be stated as
V = IR.
![]()
Question 3.
Explain the equivalent resistance of a series and parallel resistor network.
Answer:
1. Resistors in series:
When two or more resistors are connected end to end, they are said to be in series. The resistors could be simple resistors or bulbs or heating elements or other devices. Fig. (a) shows three resistors R1, R2, and R3 connected in series.
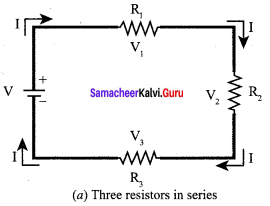
The amount of charge passing through resistor R1 must also pass through resistors R2 and R3 since the charges cannot accumulate anywhere in the circuit. Due to this reason, the current I passing through all the three resistors is the same. According to Ohm’s law, if the same current passes through different resistors of different values, then the potential difference across each resistor must be different. Let V1, V2, and V3 be the potential difference (voltage) across each of the resistors R1, R2, and R3 respectively, then we can write V1 = IR1, V2 = IR2, and V3= IR3. But the total voltage V is equal to the sum of voltages across each resistor.
V = V1 + V2 + V3
= IR1 + IR2 + IR3 ….. (1)
V = I(R1 + R2 +R3)
V = I.RS …… (2)
where Rs = R1 + R2 R3 ……. (3)
When several resistances are connected in series, the total or equivalent resistance is the sum of the individual resistances as shown in fig. (b).
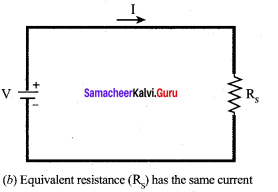
Note:
The value of equivalent resistance in series connection will be greater than each individual resistance.
2. Resistors in parallel:
Resistors are in parallel when they are connected across the same potential difference as shown in the figure.
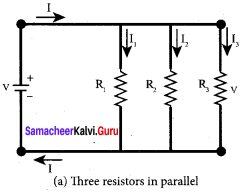
In this case, the total current I that leaves the battery is split into three separate paths. Let I1, I2, and I3 be the current through the resistors R1, R2, and R3 respectively. Due to the conservation of charge, the total current in the circuit I is equal to the sum of the currents through each of the three resistors.
I = I1 + I2 + I3 ……. (1)
Since the voltage across each resistor is the same, applying Ohm’s law to each resistor, we have
I1 = \(\frac { V }{{ R }_{1}}\) I2 = \(\frac { V }{{ R }_{2}}\),I1 = \(\frac { V }{{ R }_{3}}\)
Substituting these values in equation (1), we get
I = \(\frac { V }{{ R }_{1}}\) + \(\frac { V }{{ R }_{2}}\) +\(\frac { V }{{ R }_{3}}\) = V\(\left[ \frac { 1 }{ { R }_{ 1 } } +\frac { 1 }{ { R }_{ 2 } } +\frac { 1 }{ { R }_{ 3 } } \right] \)
I = \(\frac { V }{{ R }_{p}}\)
\(\frac { 1 }{{ R }_{p}}\) = \(\frac { 1 }{ { R }_{ 1 } } +\frac { 1 }{ { R }_{ 2 } } +\frac { 1 }{ { R }_{ 3 } } \)
Here RP is the equivalent resistance of the parallel combination of the resistors. Thus, when a number of resistors are connected in parallel, the sum of the reciprocal of the values of resistance of the individual resistor is equal to the reciprocal of the effective resistance of the combination as shown in the fig. (b).
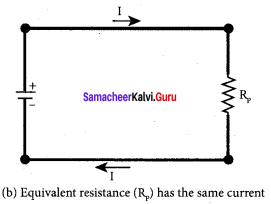
Note:
The value of equivalent resistance in parallel connections will be lesser than each individual resistance.
Question 4.
Explain the determination of the internal resistance of a cell using a voltmeter.
Answer:
Determination of internal resistance:
The emf of cell ξ is measured by connecting a high resistance voltmeter across it without connecting the external resistance R. Since the voltmeter draws very little current for deflection, the circuit may be considered as open. Hence, the voltmeter reading gives the emf of the cell. Then, external resistance R is included in the circuit and current I is established in the circuit. The potential difference across R is equal to the potential difference across the cell (V).
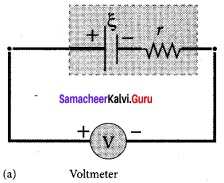
The potential drop across the resistor R is
V= IR …… (1)
Due to internal resistance r of the cell, the voltmeter reads a value V, which is less than the emf of cell ξ. It is because a certain amount of voltage (Ir) has dropped across the internal resistance r.
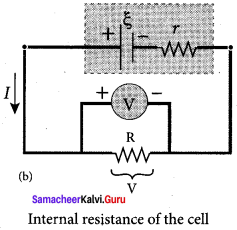
V = ξ – Ir
Ir = ξ – V …… (2)
Dividing equation (2) by equation (1), we get
\(\frac { Ir }{IR}\) = \(\frac { ξ – V }{V}\)
r = |\(\frac { ξ – V }{V}\)| R …… (3)
Since ξ, V and R are known, internal resistance r can be determined.
Question 5.
State and explain Kirchhoff’s rules.
Answer:
Kirchhoff’s first rule (current rule or junction rule):
Statement: It states that the algebraic sum of the currents at any junction of a circuit is zero. It is a statement of conservation of electric charge.
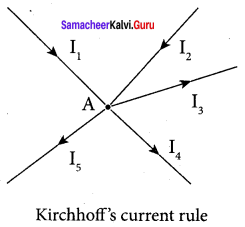
Explanation:
All charges that enter a given junction in a circuit must leave that junction since the charge cannot build up or disappear at a junction. Current entering the junction is taken as positive and current leaving the junction is taken as negative.
Applying this law to junction A,
I1 + I2 – I3 – I4 – I5 = o
Or
I1 + I2 = + I3 I4 + I5
Kirchhoff’s second rule (voltage rule or loop rule):
Statement: It states that in a closed circuit the algebraic sum of the products of the current and resistance of each part of the circuit is equal to the total emf included in the circuit. This rule follows from the law of conservation of energy for an isolated system. (The energy supplied by the emf sources is equal to the sum of the energy delivered to all resistors).
Explanation:
The product of current and resistance is taken as positive when the direction of the current is followed. Suppose if the direction of current is opposite to the direction of the loop, then the product of current and voltage across the resistor is negative. It is shown in Fig. (a) and (b). The emf is considered positive when proceeding from the negative to the positive terminal of the cell. It is shown in Fig. (c) and (d).
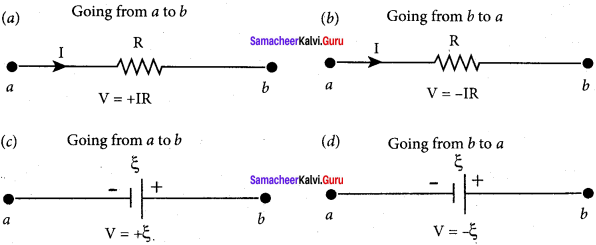
Kirchhoff voltage rule has to be applied only when all currents in the circuit reach a steady state condition (the current in various branches are constant).
Question 6.
Obtain the condition for bridge balance in Wheatstone’s bridge.
Answer:
An important application of Kirchhoff’s rules is the Wheatstone’s bridge. It is used to compare resistances and also helps in determining the unknown resistance in the electrical networks. The – bridge consists of four resistances P, Q, R, and S connected. A galvanometer G is connected between points B and D. The battery is connected between points A and C. The current through the galvanometer is IG and its resistance is G.
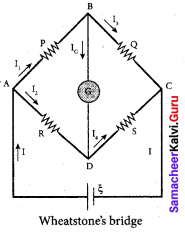
Applying KirchhofFs current rule to junction B,
I1 – IG – I3 = 0 …….. (1)
Applying Kirchhoff’s current rule to junction D,
I2 – IG – I4 = 0 …….. (2)
Applying Kirchhoff’s voltage rule to loop ABDA,
I1P + IGG – I2R = 0 …….. (3)
Applying Kirchhoff’s voltage rule to loop ABCDA,
I1P + I3Q – I4S – I2R = 0 …….. (4)
When points B and D are at the same potential, the bridge is said to be balanced.
As there is no potential difference between B and D, no current flows through the galvanometer (IG = 0).
Substituting IG = 0 in equation, (1), (2) and (3), we get
I1 = I3 …….. (5)
I2 = I4 …….. (6)
I1P = I2R …….. (7)
Substituting the equation (5) and (6) in equation (4)
I1P + I1Q – I2R = 0
I1(P + Q) = I2 (R + S) …….. (8)
Dividing equation (8) by equation (7), we get
\(\frac { P + Q }{ P }\) = \(\frac { R + S }{ R }\)
1 + \(\frac { Q }{ P }\) = 1 + \(\frac { S }{ R }\)
⇒ \(\frac { Q }{ P }\) = \(\frac { S }{ R }\)
\(\frac { P }{ Q }\) = \(\frac { R }{ S }\) …….. (9)
This is the bridge balance condition. Only under this condition, galvanometer shows null deflection. Suppose we know the values of two adjacent resistances, the other two resistances can be compared. If three of the resistances are known, the value of unknown resistance (fourth one) can be determined.
![]()
Question 7.
Explain the determination of unknown resistance using a meter bridge.
Answer:
The meter bridge is another form of Wheatstone’s bridge. It consists of a uniform manganin wire AB of one-meter length. This wire is stretched along a meter scale on a wooden board between two copper strips C and D. Between these two copper strips another copper strip E is mounted to enclose two gaps G1 and G2 An unknown resistance P is connected in G1 and a standard resistance Q is connected in G2.
A jockey (conducting wire) is connected to the terminal E on the central copper strip through a galvanometer (G) and a high resistance (HR). The exact position of a jockey on the wire can be read on the scale. A Lechlanche cell and a key (K) are connected across the ends of the bridge wire.
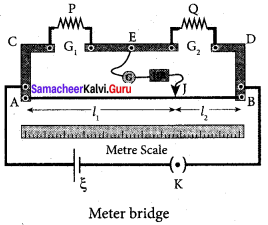
The position of the jockey on the wire is adjusted so that the galvanometer shows zero deflection. Let the point be J. The lengths AJ and JB of the bridge wire now replace the resistance R and S of the Wheatstone’s bridge. Then
\(\frac { P }{ Q }\) = \(\frac { R }{ S }\) = \(\frac { R’.AJ }{ R’.JB }\) …….. (1)
where R’ is the resistance per unit length of wire
\(\frac { P }{ Q }\) = \(\frac { AJ }{ JB }\) = \(\frac {{ l }_{1}}{ { l }_{2} }\) …….. (2)
P = Q \(\frac {{ l }_{1}}{ { l }_{2} }\) ……… (3)
The bridge wire is soldered at the ends of the copper strips. Due to imperfect contact, some resistance might be introduced at the contact. These are called end resistances. This error can be eliminated, if another set of readings are taken with P and Q interchanged and the average value of P is found.
To find the specific resistance of the material of the wire in the coil P, the radius r and length l of the wire is measured. The specific resistance or resistivity r can be calculated using the relation
Resistance = ρ-\(\frac { l }{ A }\)
By rearranging the above equation, we get
ρ = Resistance x \(\frac { A }{ l }\) …….. (4)
If P is the unknown resistance, equation (4) becomes
ρ = P\(\frac {{ πr }^{2}}{ l }\).
Question 8.
How the emf of two cells are compared using a potentiometer?
Answer:
Comparison of emf of two cells with a potentiometer:
To compare the emf of two cells, the circuit connections are made as shown in the figure. Potentiometer wire CD is connected to a battery Bt and a key K in series. This is the primary circuit. The end C of the wire is connected to the terminal M of a DPDT (Double Pole Double Throw) switch and the other terminal N is connected to a jockey through a galvanometer G and a high resistance HR. The cells whose emf ξ1 and ξ2 to be compared are connected to the terminals M1, N1 and M2, N2 of the DPDT switch.
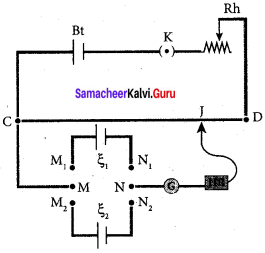
The positive terminals of Bt, ξ1, and ξ2 should be connected to the same end C. The DPDT switch is pressed towards M1, N1 so that cell ξ1 is included in the secondary circuit and the balancing length l1 is found by adjusting the jockey for zero deflection, Then the second cells ξ2 is included in the circuit and the balancing length l2 is determined. Let r be the resistance per unit length of the potentiometer wire and I be the current flowing through the wire.
we have.
ξ1 = Irl1 …… (1)
ξ2 = Irl2 ……. (2)
By dividing (1) by (2)
\(\frac {{ ξ }^{1}}{ { ξ }^{2} }\) = \(\frac {{ l }^{1}}{ { l }^{2} }\) ……. (3)
By including a rheostat (Rh) in the primary circuit, the experiment can be repeated several times by changing the current flowing through it.
Samacheer Kalvi 12th Physics Current Electricity Numerical Problems
Question 1.
The following graphs represent the current versus voltage and voltage versus current for the six conductors A, B, C, D, E, and F. Which conductor has the least resistance and which has maximum resistance?
Solution:
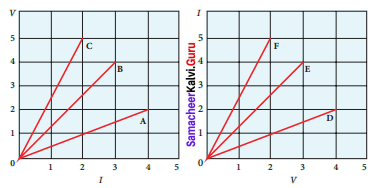
According to ohm’s law, V = IR
Resistance of conductor, R = \(\frac { V }{ I }\)
Graph-I:
Conductor A, I = 4 A and V = 2 V
R = \(\frac { V }{ I }\) = \(\frac { 2 }{ 4 }\) = 0.5 Ω
Conductor B, I = 3 A and V = 4 V
R = \(\frac { V }{ I }\) = \(\frac { 4 }{ 3 }\) = 1.33 Ω
Conductor C, I = 2 A and V = 5 V
R= \(\frac { V }{ I }\) = \(\frac { 5 }{ 2 }\) = 2.5 Q Ω.
Graph-II:
Conductor D, I = 2 A and V = 4 V
R = \(\frac { V }{ I }\) = \(\frac { 4 }{ 2 }\) = 2 Ω d
Conductor E, I = 4A and V = 3 V
R = \(\frac { V }{ I }\) = \(\frac { 3 }{ 4 }\) = 1.75 Ω
Conductor F, I = 5A and V = 2 V
R = \(\frac { V }{ I }\) = \(\frac { 2 }{ 5 }\) = 0.4 Ω
Conductor F has the least resistance, RF = 0.4 Ω,
Conductor C has maximum resistance, RC = 2.5 G.
Question 2.
Lightning is a very good example of a natural current. In typical lightning, there is 109 J energy transfer across the potential difference of 5 x 107 V during a time interval of 0.2 s.

Using this information, estimate the following quantities
(a) the total amount of charge transferred between cloud and ground
(b) the current in the lightning bolt
(c) the power delivered in 0.2 s.
Solution:
During the lightning energy, E = 109 J
Potential energy, V = 5 x 107 V
Time interval, t = 0.2 s
(a) Amount of charge transferred between cloud and ground,
q = It
(b) Current in the lighting bolt, E = VIt
I = \(\frac { E }{ Vt }\) = \(\frac{10^{9}}{5 \times 10^{7} \times 0.2}\) = 1 × 109 × 1-7
I = 1 × 102
I = 100 A
∴ q = It = 100 × 0.2
q = 20 C.
(c) Power delivered, E = VIt
P = VI = 5 × 107 × 100 = 500 × 107
I = 5 × 109 W
P = 5 GW.
Question 3.
A copper wire of 106 m2 area of cross-section, carries a current of 2 A. If the number of electrons per cubic meter is 8 x 1028, calculate the current density and average drift velocity.
Solution:
Cross-sections area of copper wire, A = 106 m2
I = 2A
Number of electron, n = 8 x 1028
Current density, J = \(\frac { 1 }{ A }\) = \(\frac { 2 }{{ 10 }^{-6}}\)
J = 2 × 106 Am-2
Average drift velocity, Vd = \(\frac { 1 }{ neA }\)
e is the charge of electron = 1.6 × 10-9 C
Vd = \(\frac{2}{8 \times 10^{28} \times 1.6 \times 10^{-19} \times 10^{-6}}\) = \(\frac { 1 }{{ 64. × 10 }{3}}\)
Vd = 0.15625 × 10-3
Vd = 15.6 × 10-5 ms-1
![]()
Question 4.
The resistance of a nichrome wire at 0 °C is 10 Ω. If its temperature coefficient of resistance is 0.004/°C, find its resistance at the boiling point of water. Comment on the result.
Solution:
The resistance of a nichrome wire at 0°C, R0 = 10 Ω
Temperature coefficient of resistance, α = 0.004/°C
Resistance at the boiling point of water, RT =?
The temperature of the boiling point of water, T = 100 °C
RT=R0 ( 1 + αT) = 10[1 + (0.004 x 100)]
RT= 10(1 +0.4) = 10 x 1.4
RT = 14 Ω
As the temperature increases, the resistance of the wire also increases.
Question 5.
The rod given in the figure is made up of two different materials.

Both have square cross-sections of 3 mm side. The resistivity of the first material is 4 x 10-3 Ω.m and it is 25 cm long while the second material has a resistivity of 5 x 10-3 Ω.m and is of 70 cm long. What is the resistivity of the rod between its ends?
Solution:
Square cross section of side, a = 3 mm = 3 x 10-3 m
Cross section of side, A = a2 = 9 x 106 m
First material:
Resistivity of the material, ρ1 = 4 x 10-3 Ωm
length, l1 = 25 cm = 25 x 10-2 m
Resistance of the lord, R1 = \(\frac{\rho_{l} l_{l}}{A}\) = \(\frac{4 \times 10^{-3} \times 25 \times 10^{-2}}{9 \times 10^{-6}}\) = \(\frac{100 \times 10^{-5} \times 10^{6}}{9}\)
R1 = 11.11 x 101 Ω
Second material:
Resistivity of the material, ρ2 = 5 x 10-3 Ωm
length, l2 = 70 cm = 70 x 10-2 m
Resistance of the rod, R2 = \(\frac{\rho_{2} l_{2}}{A}\) = \(\frac{5 \times 10^{-3} \times 70 \times 10^{-2}}{9 \times 10^{-6}}\) = \(\frac{350 \times 10^{-5} \times 10^{6}}{9}\)
R2 = 38.88 x 101
R2 = 389 Ω
Total resistance between the ends f the rods
R = R1 + R2 = 111 + 389 = 500 Ω
Question 6.
Three identical lamps each having a resistance R are connected to the battery of emf as shown in the figure.
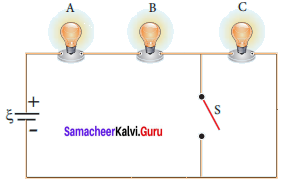
Suddenly the switch S is closed
(a) Calculate the current in the circuit when S is open and closed
(b) What happens to the intensities of the bulbs A, B, and C.
(c) Calculate the voltage across the three bulbs when S is open and closed
(d) Calculate the power delivered to the circuit when S is opened and closed
(e) Does the power delivered to the circuit decreases, increases or remain the same?
Solution:
The resistance of the identical lamp = R
Emf of the battery = ξ
According to Ohm’s Law, ξ = IR
(a) Current:
When Switch is open— The current in the circuit. Total resistance of the bulb,
Rs = R1 + R2 + R3
R1 = R2 = R3 = R
Rs = R + R + R = 3R
∴ Current, I = \(\frac { ξ }{{ R }_{s}}\)
⇒ I0 = \(\frac { ξ }{ 3R }\)
Switch is closed— The current in the circuit. Total resistance of the bulb,
Rs = R + R = 2R
Current I = \(\frac { ξ }{{ R }_{s}}\)
Ic = \(\frac { ξ }{ 2R }\).
(b) Intensity:
When the switch is open — All the bulbs glow with equal intensity.
When the switch is closed — The intensities of the bulbs A and B equally increase. Bulb C will not glow since no current passes through it.
(c) Voltage across three bulbs:
When switch is open — Voltage across bulb A, VA = I0 R = \(\frac { ξ }{ 3R }\) x R = \(\frac { ξ }{ 3 }\)
similarly:
Voltage across bulb B, VB = \(\frac { ξ }{ 3 }\)
Voltage across bulb C, VC = \(\frac { ξ }{ 3 }\)
When switch is closed— Voltage across bulb A, VA = IcR = \(\frac { ξ }{ 2R }\) x \(\frac { ξ }{ 2 }\)
similarly:
Voltage across bulb B, VB = IcR \(\frac { ξ }{ 2 }\)
Voltage across bulb C, VC = 0
(d) Power delivered to the circuit,
When the switch is opened — Power P, = VI
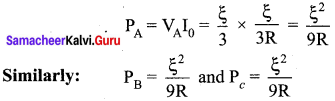
When the switch is closed — Power P, = VI

(e) Total power delivered to the circuit increases.
Question 7.
The current through an element is shown in the figure. Determine the total charge that passes through the element at
(a) t = 0 s
(b) t = 2 s
(c) t = 5 s
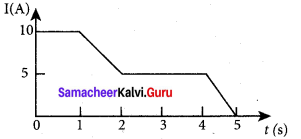
Solution :
Rate of flow of charge is called current, I = \(\frac { dq }{ dt }\)
Total charge pass through element, dq = Idt
(a) At t = 0 s, I = 10 A
dq = Idt= 10 x 0 = 0 C.
(b) At t = 2 s, I = 5 A
dq = Idt = 5 x 2 = 10 C.
(c) At t = 5 s, I = 0
dq = Idt = 0 x 5 = 0 C.
![]()
Question 8.
An electronics hobbyist is building a radio which requires 150 Ω in her circuit, but she has only 220Ω, 79Ω, and 92Ω resistors available. How can she connect the available resistors to get the desired value of resistance?
Solution:
Required effective resistance = 150 Ω
Given resistors of resistance, R1 = 220 Ω, R2 = 79 Ω, R3 = 92 Ω
Parallel combination R1 and R2
\(\frac { 1 }{{ R }_{p}}\) = \(\frac { 1 }{{ R }_{1}}\) + \(\frac { 1 }{{ R }_{2}}\) = \(\frac { 1 }{ 220 }\) + \(\frac { 1 }{ 79 }\) = \(\frac { 79 + 220 }{ 220 × 79 }\)
Rp = 58 Ω
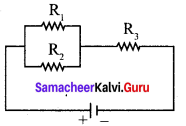
Parallel combination Rp and R3
Rs = Rp + R3 = 58 + 92
Rs = 150 Ω
Parallel combination of 220 Ω and 79 Ω in series with 92 Ω.
Question 9.
A cell supplies a current of 0.9 A through a 2 Ω resistor and a current of 0.3 A through a 7 Ω resistor. Calculate the internal resistance of the cell.
Solution:
Current from the cell, I1 = 0.9 A
Resistor, R1 = 2 Ω
Current from the cell, I2 = 0.3 A
Resistor, R2 7 Ω
The internal resistance of the cell, r =?
Current in the circuit I1 = \(\frac { ξ }{{ r + R }_{1}}\)
ξ = I1 (r + R1) …… (1)
Current in the circuit, I2 = \(\frac { ξ }{{ r + R }_{2}}\) …… (2)
Equating equation (1) and (2),
I1r + I1R1 = I2R2 + I2r
(I1 – I2)r = I2R2 – I1R1
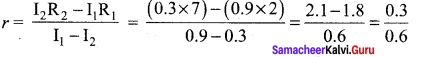
r = 0.5 Ω.
Question 10.
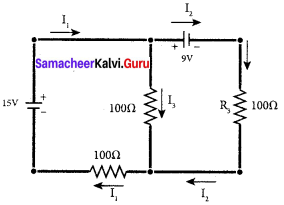
Calculate the currents in the following circuit.
Solution:
Applying Kirchoff’s 1st Law at junction B
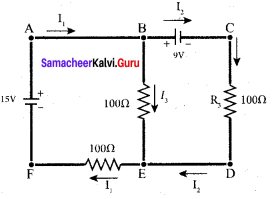
I1 – I1 – I3 = 0
I3 = I1 – I2 …… (1)
Applying Kirchoff’s IInd Law at junction in ABEFA
100 I3 + 100 I1 = 15
100 (I3 + I1) = 15
100 I1 – 100 I2 + 100 I1 =15
200 I1 – 100 I2 = 15 …… (2)
Applying Kirchoff’s IInd Law at junction in BCDED
-100I2 + 100 I3 = 9
-100 I2+ 100(I1 – I2) = 9
100I1 – 200 I2 = 9
Solving equating (2) and (3)

Substitute I1 values in equ (2)
200(0.07) – 100 I2 = 15
14 – 100 I2 = 15
– 100 I2 = 15 – 14
I2 = \(\frac { -1 }{ 100 }\)
I2 = -0.01A
Substitute I1 and I2 value in equ (1), we get
I3 = I1 – I2 = 0.07 – (-0.01)
I3 = 0.08 A.
Question 11
A potentiometer wire has a length of 4 m and a resistance of 20 Ω. It is connected in series with the resistance of 2980 Ω and a cell of emf 4 V. Calculate the potential along the wire.
Solution:
Length of the potential wire, l = 4 m
Resistance of the wire, r = 20 Ω
Resistance connected series with potentiometer wire, R = 2980 Ω
Emf of the cell, ξ = 4 V
Effective resistance, Rs = r + R = 20 + 2980 = 3000 Ω
Current flowing through the wire, I = \(\frac { ξ }{{ r + R }_{s}}\) = \(\frac { 4 }{ 3000 }\)
I = 1.33 x 10-3 A
Potential drop across the wire, V = Ir = 1.33 x 10-33 x 20
V = 26.6 x 10-3 V

= 6.65 x 10-3
Potential garadient = 0.66 x 10-2 Vm-1
Question 12.
Determine the current flowing through the galvanometer (G) as shown in the figure.
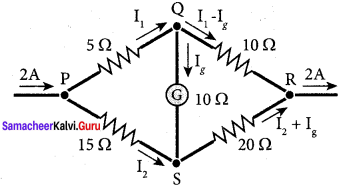
Solution:
Current flowing through the circuit, I = 2A
Applying Kirchoff’s Ist law at junction P, I = I1 + I2
I2 = I – I1 …(1)
Applying Kirchoff’s Ind law at junction PQSP
5 I1 + 10 Ig – 15 I2 = 0
5 I1 + 10 Ig -15(I – I1) = 0
20 I1 + 10 Ig = 15 I
20 I1 + 10 Ig = 15 x 2
÷ by 10 21 I1 + Ig = 3 … (2)
Applying Kirchoff’s IInd law at junction QRSQ
10(I1 – Ig) – 20(I – I1 – Ig) – 10 Ig = 0
10 I1 – 10g – 20(I – I1 – Ig) – 10 Ig = 0
10 I1 – 10g – 20 I + 20 I1 -20Ig – 10 Ig = 0
30 I 1 – 40 Ig = 20 I
÷ by 10 ⇒ 3 I1 – 4 Ig = 20 I
3 I1 – 4 Ig = 2 I
3 I1 – 4 Ig = 2 x 2 = 4
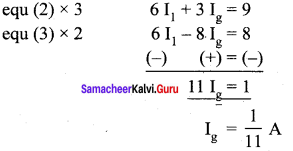
Question 13.
Two cells each of 5 V are connected in series across an 8 Ω resistor and three parallel resistors of 4 Ω, 6 Ω, and 12 Ω. Draw a circuit diagram for the above arrangement. Calculate
(i) the current drawn from the cell
(ii) current through each resistor.
Solution:
V1 = 5 V; V2 = 5 V
R1 = 8 Ω; R2 = 4 Ω; R3 = 6 Ω; R4 = 12 Ω
Three resistors R2, R3, and R4 are connected parallel combination
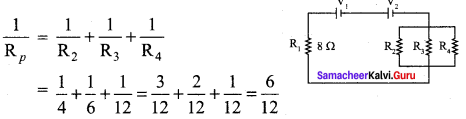
Resistors R1 and Rp are connected in series combination
Rs = R1 +Rp = 8 + 2 = 10
Rs = 10Ω
Total voltage connected series to the circuit
V = V1 + V2
= 5 + 5 = 10
V = 10 V.
(i) Current through the circuit, I = \(\frac { V }{{ R }_{s}}\) = \(\frac { 10 }{ 10 }\)
I = 1 A
Potential drop across the parallel combination,
V’ = IRp = 1 x 2
V’ = 2 V
(ii) Current in 4 Ω resistor, I = \(\frac { V’ }{{ R }_{2}}\) = \(\frac { 2 }{ 4 }\) = 0.5 A
Current in 6 Ω resistor, I = \(\frac { V’ }{{ R }_{3}}\) = \(\frac { 2 }{ 6 }\) = 0.33 A
Current in 12 Ω resistor, I = \(\frac { V’ }{{ R }_{4}}\) = \(\frac { 2 }{ 12 }\) = 0.17 A
![]()
Question 14.
Four light bulbs P, Q, R, S are connected in a circuit of unknown arrangement. When each bulb is removed one at a time and replaced, the following behavior is observed.

Solution:
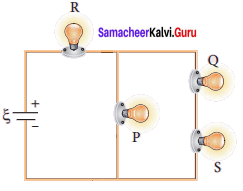
Question 15.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63 cm, what is the emf of the second cell?
Solution:
Emf of the cell1, ξ1 = 1.25 V
Balancing length of the cell, l1 = 35 cm = 35 x 10-2 m
Balancing length after interchanged, l2 = 63 cm = 63 x 10-2 m
Emf of the cell1, ξ2 = ?
The ration of emf’s, \(\frac {{ ξ }_{1}}{{ ξ }_{2}}\) = \(\frac {{ l }_{1}}{{ l }_{2}}\)
The ration of emf’s, ξ2 = ξ1 = \(\left( \frac { { l }_{ 2 } }{ { l }_{ 1 } } \right) \)
= 1. 25 x \(\left( \frac { { 63×10 }^{ -2 } }{ { 35×10 }^{ -2 } } \right) \) = 12.5 x 1.8
ξ2 = 2.25 V.
Samacheer Kalvi 12th Physics Current Electricity Additional Questions Solved
I. Choose the Correct Answer
Question 1.
When current I flows through a wire, the drift velocity of the electrons is v. When current 21 flows through another wire of the same material having double the length and area of cross-section, the drift velocity of the electrons will be-
(a) \(\frac { v }{ 4 }\)
(b) \(\frac { v }{ 2 }\)
(c) v
(d) 2 v
Answer:
(c) v
Hint:
Vd = \(\frac { 1 }{ nAe }\); v’d = \(\frac { 2I }{ (2A)ne }\) = vd
Question 2.
A copper wire of length 2 m and area of cross-section 1.7 x 10-6 m2 has a resistance of 2 x 10-2 Ω. The resistivity of copper is
(a) 1.7 x 10-8 Ωm
(b) 1.9 x -8 Ωm
(c) 2.1 x 10-7 Ωm
(d) 2.3 x 10-7 Ωm
Answer:
(a) 1.7 x 10-8 Ωm
Hint:
Resistivity, ρ = \(\frac { RA }{ l }\) = \(\frac{2 \times 10^{-2} \times 1.7 \times 10^{-6}}{2}\) = 1.7 x 10-8 Ωm.
Question 3.
If the length of a wire is doubled and its cross-section is also doubled, then its resistance will
(a) become 4 times
(b) become 1 / 4
(c) becomes 2 times
(d) remain unchanged
Answer:
(d) remain unchanged
Question 4.
A 10 m long wire of resistance 20 Ω is connected in series with a battery of emf 3 V and a resistance of 10 Ω. The potential gradient along the wire in volt per meter is
(a) 6.02
(b) 0.1
(c) 0.2
(d) 1.2
Answer:
(c) 0.2
Hint:
Potential difference across the wire = \(\frac { 20 }{ 3 }\) x 3 = 2 V
Potential gradient = \(\frac { v }{ l }\) = \(\frac { 2 }{ 10 }\) = 0.2 V/m
![]()
Question 5.
The resistivity of a wire
(a) varies with its length
(b) varies with its mass
(c) varies with its cross-section
(d) does not depend on its length, cross-section, and mass.
Answer:
(d) does not depend on its length, cross-section, and mass.
Question 6.
The electric intensity E, current density and conductivity a are related as
(a) j = σE
(b) j = \(\frac { E }{ σ }\)
(c) JE = s
(d) j = σ2E
Answer:
(a) j = σE
Question 7.
For which of the following dependences of drift velocity Vd on electric field E, is Ohm’s law obeyed?
(a) vd ∝ E
(b) vd ∝ E2
(c) vd ∝ √E
(d) vd = constant
Answer:
(a) vd ∝ E
Hint:
vd = \(\frac { 1 }{ nAe }\) = \(\frac { j }{ ne }\) = \(\left( \frac { σ }{ ne } \right) \)E ⇒ vd ∝ E.
Question 8.
A cell has an emf of 1.5 V. When shortcircuited, it gives a current of 3A. The internal resistance of the cell is
(a) 0.5 Ω
(b) 2.0 Ω
(c) 4.5 Ω
(d) \(\frac { 1 }{ 4.5 }\) Ω
Answer:
(a) 0.5 Ω
Hint:
r = \(\frac { ξ }{ I }\) = \(\frac { 1.5 }{ 3 }\) = 0.5 Ω.
![]()
Question 9.
The resistance, each of 1 Ω, are joined in parallel. Three such combinations are put in series. The resultant resistance is
(a) 9 Ω
(b) 3 Ω
(c) 1 Ω
(d) \(\frac { 1 }{ 3 }\) Ω
Answer:
(c) 1 Ω
Hint:
Rp = 1 + 1 + 1 = 3 Ω;
\(\frac { 1 }{{ R }_{s}}\) = \(\frac { 1 }{ 3 }\) + \(\frac { 1 }{ 3 }\) + \(\frac { 1 }{ 3 }\) = \(\frac { 3 }{ 3 }\) = 1
⇒ Rs = 1 Ω.
Question 10.
Constantan is used for making standard resistance because it has
(a) high resistivity
(b) low resistivity
(c) negligible temperature coefficient of resistance
(d) high melting point
Answer:
(c) negligible temperature coefficient of resistance
Question 11.
Kirchhoff’s two laws for electrical circuits are manifestations of the conservation of
(a) charge only
(b) both energy and momentum
(c) energy only
(d) both charge and energy
Answer:
(d) both charge and energy
Question 12.
The resistance R0 and Rt of a metallic wire at temperatures 0° C and t° C are related as (a is the temperature coefficient of resistance).
(a) Rt = R0(1 + αt)
(b) Rt = R0(1 – αt)
(c) Rt = R0(1 + αt)2
(d) Rt = R0(1 – αt) 2
Answer:
(a) Rt = R0(1 + αt)
Question 13.
A cell of emf 2 V and internal resistance 0.1 Ω is connected with a resistance of 3.9 Ω. The voltage across the cell terminals will be
(a) 0.5 V
(b) 1.9 V
(c) 1.95 V
(d) 2 V
Answer:
(c) 1.95 V
Hint:
V = \(\frac { ER }{ R + r }\) = \(\frac { 2 x 3.9 }{ 3.9 + 0.1 }\) = 1.95 V.
Question 14.
A flow of 107 electrons per second in a conduction wire constitutes a current of
(a) 1.6 x 10-26 A
(b) 1.6 x 1012 A
(c) 1.6 x 10-12 A
(d) 1.6 x 1026 A
Answer:
(c) 1.6 x 10-12 A
Hint:
I = \(\frac { Q }{ t }\) = \(\frac{10^{7} \times 1.6 \times 10^{-19}}{1}\) = 1.6 x 1012 A.
Question 15.
The sensitivity of a potentiometer can be increased by
(a) increasing the emf of the cell
(b) increasing the length of the wire
(c) decreasing the length of the wire
(d) none of the above
Answer:
(b) increasing the length of the wire
![]()
Question 16.
The potential gradient is defined as
(a) fall of potential per unit length of the wire.
(b) fall of potential per unit area of the wire.
(c) fall of potential between two ends of the wire.
(d) none of the above.
Answer:
(a) fall of potential per unit length of the wire.
Question 17.
n equal resistors are first connected in series and then in parallel. The ratio of the equivalent resistance in two cases is
(a) n
(b) \(\frac { 1 }{{ n }^{2}}\)
(c) n2
(d) \(\frac { 1 }{ n }\)
Answer:
(c) n2
Hint:
Required ratio = \(\frac{n \mathrm{R}}{\left(\frac{\mathrm{R}}{n}\right)}\) = n(c) n2
Question 18.
A galvanometer is converted into an ammeter when we connect a
(a) high resistance in series
(b) high resistance in parallel
(c) low resistance in series
(d) low resistance in parallel
Answer:
(d) low resistance in parallel
Question 19.
The reciprocal of resistance is
(a) conductance
(b) resistivity
(c) conductivity
(d) none of the above
Answer:
(a) conductance
Question 20.
A student has 10 resistors, each of resistance r. The minimum resistance that can be obtained by him using these resistors is
(a) 10r
(b) \(\frac { r }{ 10 }\)
(c) \(\frac { r }{ 100 }\)
(d) \(\frac { r }{ 5 }\)
Answer:
(b) \(\frac { r }{ 10 }\)
Question 21.
The drift velocity of electrons in a wire of radius r is proportional to
(a) r
(b) r2
(c) r3
(d) none of the above
Answer:
(d) none of the above
Question 22.
Kirchhoff’s first law, i.e. ∑I = 0 at a junction deals with the conservation of
(a) charge
(b) energy
(c) momentum
Answer:
(a) charge
![]()
Question 23.
The resistance of a material increases with temperature. It is a
(a) metal
(b) insulator
(c) semiconductor
(d) semi-metal
Answer:
(a) metal
Question 24.
Five cells, each of emf E, are joined in parallel. The total emf of the combination is
(a) 5E
(b) \(\frac { E }{ 5 }\)
(c) E
(d) \(\frac { 5E }{ 2 }\)
Answer:
(c) E
Question 25.
A carbon resistance has colour bands in order yellow, brown, red. Its resistance is
(a) 41 Ω
(b) 41 x 102 Ω
(c) 41 x 103 Ω
(d) 4.2 Ω
Answer:
(b) 41 x 102 Ω
Question 26.
The conductivity of a superconductor is
(a) infinite
(b) very large
(c) very small
(d) zero
Answer:
(a) infinite
Question 27.
The resistance of an ideal voltmeter is
(a) zero
(b) very high
(c) very low
(d) infinite
Answer:
(d) infinite
Question 28.
Carriers of electric current in superconductors are
(a) electrons
(b) photons
(c) holes
Answer:
(c) holes
![]()
Question 29.
Potentiometer measures potential more accurately because
(a) It measure potential in the open circuit.
(b) It uses sensitive galvanometer for null detection.
(c) It uses high resistance potentiometer wire.
(d) It measures potential in the closed circuit.
Answer:
(a) It measures potential in the open circuit.
Question 30.
Electromotive force is most closely related to
(a) electric field
(b) magnetic field
(c) potential difference
(d) mechanical force
Answer:
(c) potential difference
Question 31.
The capacitance of a pure capacitor is 1 farad. In DC circuit, the effective resistance will be
(a) zero
(b) infinite
(c) 1 Ω
(d) 0.5 Ω
Answer:
(b) infinite
![]()
Question 32.
The resistance of an ideal ammeter is
(a) zero
(b) small
(c) high
(d) infinite
Answer:
(a) zero
Question 33.
A milliammeter of range 10 mA has a coil of resistance 1 Ω. To use it as a voltmeter of range 10 V, the resistance that must be connected in series with it is
(a) 999 Ω
(b) 1000 Ω
(c) 9 Ω
(d) 99 Ω
Answer:
(a) 999 Ω
Hint:
R = \(\frac { V }{{ I }_{g}}\)-Rg = \(\frac { 10 }{{ 10 × 10 }^{-3}}\)-1 = 999 Ω.
Question 34.
A battery of emf 10 V and internal resistance 3 Ω is connected to a resistor. The current in the circuit is. 0.5 A. The terminal voltage of the battery when the circuit is closed is
(a) 10 V
(b) zero
(c) 8.5 V
(d) 1.5 V
Answer:
(c) 8.5 V
Hint:
V = ξ – Ir = 10 – (0.5 x 3) = 8.5 V.
Question 35.
Good resistance coils are made of
(a) copper
(b) manganin
(c) iron
(d) aluminum
Answer:
(b) manganin
![]()
Question 36.
A wire of resistance R is stretched to three times its original length. The new resistance is
(a) 3R
(b) 9R
(c) R/3
(d) R/9
Answer:
(b) 9R
Question 37.
n resistances, each of r Ω, when connected in parallel give an equivalent resistance of R Ω. If these resistances were connected in series, the combination would have resistance in horns equal to
(a) n2R
(b) \(\frac { R }{{n}^{ 2 }}\)
(c) \(\frac { R }{ n }\)
(d) nR
Answer:
(a) n2R
Hint:
Resistance in parallel combination, R = \(\frac { r }{ n }\) ⇒ r = Rn
Resistance in series combination, R’ = nr = n2R
Question 38.
When a wire of uniform cross-section, having resistance R, is bent into a complete circle, the resistance between any two of diametrically opposite points will be
(a) \(\frac { R }{ 8 }\)
(b) \(\frac { R }{ 2 }\)
(c) 4R
(d) \(\frac { R }{ 4 }\)
Answer:
(d) \(\frac { R }{ 4 }\)
Hint:
It becomes two resistors each of (d) \(\frac { R }{ 2 }\), connected in parallel.
Question 39.
A steady current is set up in a metallic wire of a non-uniform cross-section. How is the rate of flow K of electrons related to the area of cross-section A?
(a) K is independent of A
(b) K ∝ A
(c) K ∝ A-1
(d) K ∝ A2
Answer:
(c) K ∝ A-1
Question 40.
Ohm’s Law is not obeyed by
(a) electrolytes
(b) discharge tubes
(c) vacuum tubes
(d) all of these
Answer:
(d) all of these
![]()
Question 41.
Which of the following has a negative temperature coefficient of resistance?
(a) Copper
(b) Aluminium
(c) Germanium
(d) Iron
Answer:
(c) Germanium
II. Fill in the blanks
Question 1.
The material through which electric charge can flow easily is ……………….
Answer:
Copper.
Question 2.
A toaster operating at 240 V has a resistance of 120 Ω. The power is ……………….
Answer:
480 W.
Question 3.
In the case of insulators, as the temperature decreases, resistivity ……………….
Answer:
Increases.
Question 4.
When n resistors of equal resistance (R) are connected in series, the effective resistance is ……………….
Answer:
nR.
Question 5.
The net flow of charge at any point in the conductor is ……………….
Answer:
Zero.
![]()
Question 6.
The flow of free electrons in a conductor constitutes ……………….
Answer:
Electric current.
Question 7.
The rate of flow of charge through any wire is called ……………….
Answer:
Current.
Question 8.
The drift velocity acquired per unit electric field is the ……………….
Answer:
Mobility.
Question 9.
The reciprocal of resistance is ……………….
Answer:
Conductance.
Question 10.
The unit of specific resistance is ……………….
Answer:
Ohm meter.
Question 11.
The reciprocal of electrical resistivity is called ……………….
Answer:
Electrical conductivity.
Question 12.
With increase in temperature the resistivity of metals ……………….
Answer:
Increases.
![]()
Question 13.
The resistivity of insulators is of the order of ……………….
Answer:
108 1014 Ωm.
Question 14.
The resistivity of semiconductors is of the order of ……………….
Answer:
10-2 -102 Ωm.
Question 15.
The materials which conduct electricity at zero resistance are called ……………….
Answer:
Superconductors.
Question 16.
Conductors turn into superconductors at ……………….
Answer:
Low temperatures.
Question 17.
The resistance of superconductors is ……………….
Answer:
Zero.
Question 18.
The phenomenon of superconductivity was discovered by ……………….
Answer:
Kammerlingh onnes.
Question 19.
Mercury becomes a superconductor at ……………….
Answer:
4.2 K.
Question 20.
With the increase of temperature, the resistance of conductors ……………….
Answer:
increases
![]()
Question 21.
In insulators and semiconductors, as temperature increases, resistance ……………….
Answer:
Decreases.
Question 22.
A material with a negative temperature coefficient is called a ……………….
Answer:
Thermistor.
Question 23.
The temperature coefficient for alloys is ……………….
Answer:
Low.
Question 24.
The electric current in an external circuit flows from the ……………….
Answer:
Positive to the negative terminal.
Question 25.
In the electrolyte of the cell, current flows from ……………….
Answer:
Negative to the positive terminal.
Question 26.
A freshly prepared cell has ………………. internal resistance.
Answer:
Low.
Question 27.
Kirchhoff’s first law is ……………….
Answer:
Current law.
![]()
Question 28.
The current law states that the algebraic sum of the currents meeting at any junction in a circuit is ……………….
Answer:
Zero.
Question 29.
Current law is a consequence of conservation of ……………….
Answer:
Charges.
Question 30.
Kirchhoff’s second law is ……………….
Answer:
Voltage law.
Question 31.
Kirchhoff’s second law is a consequence of conservation of ……………….
Answer:
Energy.
Question 32.
Wheatstone bridge is an application of ……………….
Answer:
Kirchhoff’s Law.
Question 33
………………. is a form of Wheatstone’s bridge.
Answer:
Metre bridge.
Question 34.
The temperature coefficient of manganin wire is ……………….
Answer:
Low.
Question 35
………………. is an instrument to measure the potential difference.
Answer:
Potentiometer.
![]()
Question 36.
Unit of electrical energy is ……………….
Answer:
Joule.
Question 37.
An instrument to measure electrical power consumed is ……………….
Answer:
Wattmeter.
Question 38.
………………. first introduced the electrochemical battery
Answer:
Volta.
Question 39.
Charging is a process of reproducing ……………….
Answer:
Active materials.
III. Match the following
Question 1.

Answer:
(i) → (b)
(ii) → (a)
(iii) → (d)
(iv) →(c)
Question 2.

Answer:
(i) → (b)
(ii) → (c)
(iii) → (d)
(iv) → (a)
Question 3.

Answer:
(i) → (d)
(ii) → (c)
(iii) → (b)
(iv) → (a)
Question 4.

Answer:
(i) → (b)
(ii)→ (d)
(iii) → (a)
(iv) → (c)
IV.Assertion and reason type
(a) If both assertion and reason are true and the reason in the correct explanation of the assertion.
(b) If both assertion and reason are true but the reason is not correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If the assertion and reason both are false.
(e) If assertion is false but reason is true.
Question 1.
Assertion: Fuse wire must have high resistance and low melting point.
Reason: Fuse is used for small current flow only
Answer:
(c) If assertion is true but reason is false.
Question 2.
Assertion: In practical application, power rating of resistance is not important.
Reason: Property of resistance remains same even at high temperature
Answer:
(d) If the assertion and reason both are false.
![]()
Question 3.
Assertion: Electric appliances with metallic body e.g. heaters, presses, etc, have three pin connections, whereas an electric bulb has two pins.
Reason: Three pin connection reduce heating of connecting cables.
Answer:
(c) If assertion is true but reason is false.
Samacheer Kalvi 12th Physics Current Electricity Short Answer Questions
Question 1.
Define current?
Answer:
Current is defined as a net charge Q passes through any cross-section of a conductor in time t
then, I = \(\frac { Q }{ t }\).
Question 2.
Define instantaneous current?
Answer:
The instantaneous current I is defined as the limit of the average current, as ∆t → 0.
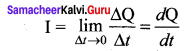
Question 3.
What is resistance? Give its unit?
Answer:
The resistance is the ratio of potential difference across the given conductor to the current passing through the conductor V.
R = \(\frac { V }{ I }\).
Question 4.
What is meant by transition temperature?
Answer:
The resistance of certain materials become zero below certain temperature Tc. This temperature is known as critical temperature or transition temperature.
Question 5.
What is Joule’s heating effect?
Answer:
When current flows through a resistor, some of the electrical energy delivered to the resistor is converted into heat energy and it is dissipated. This heating effect of current is known as Joule’s heating effect.
![]()
Question 6.
What is meant by the thermoelectric effect?
Answer:
Conversion of temperature differences into electrical voltage and vice versa is known as the thermoelectric effect.
Question 7.
What is a thermopile? On what principle does it work?
Answer:
Thermopile is a device used to detect thermal radiation. It works on the principle of seebeck effect.
Question 8.
What is a thermistor?
Answer:
A material with a negative temperature coefficient is called a thermistor.
Eg:
- Insulator
- Semiconductor.
Question 9.
State principle of a potentiometer?
Answer:
The principle of a potentiometer states that the emf of the cell is directly proportional to its balancing length.
ξ ∝ l
ξ = Irl.
Samacheer Kalvi 12th Physics Current Electricity Long Answer Questions
Question 1.
Explain the concept of colour code for carbon resistors.
Answer:
Color code for Carbon resistors:
Carbon resistors consist of a ceramic core, on which a thin layer of crystalline carbon is deposited. These resistors are inexpensive, stable, and compact in size. Color rings are used to indicate the value of the resistance according to the rules.
Three coloured rings are used to indicate the values of a resistor: the first two rings are significant figures of resistances, the third ring indicates the decimal multiplier after them. The fourth color, silver or gold, shows the tolerance of the resistor at 10% or 5%. If there is no fourth ring, the tolerance is 20%. For the resistor, the first digit = 5 (green), the second digit = 6 (blue), decimal multiplier = 103 (orange) and tolerance = 5% (gold). The value of resistance = 56 x 103 Q or 56 kΩ with the tolerance value of 5%.
Question 2.
Explain in details of the temperature dependence of resistivity.
Answer:
Temperature dependence of resistivity:
The resistivity of a material is dependent on temperature. It is experimentally found that for a wide range of temperatures, the resistivity of a conductor increases with an increase in temperature according to the expression,
ρT = ρ0 [1 + α(T -T0)] ……. (1)
where ρT is the resistivity of a conductor at T0C, ρ0 is the resistivity of the conductor at some reference temperature To (usually at 20°C) and a is the temperature coefficient of resistivity. It is defined as the ratio of increase in resistivity per degree rise in temperature to its resistivity atT0.
From the equation (1), we can write
ρT – ρ0 = αρ0 (T -T0)
∴ α = \(\frac{\rho_{\mathrm{T}}-\rho_{0}}{\rho_{0}\left(\mathrm{T}-\mathrm{T}_{0}\right)}\) = \(\frac{\Delta p}{\rho_{0} \Delta T}\)
where ∆ρ = ρT – ρ0 is change in resistivity for a change in temperature ∆T = T – T0. Its unit is per °C.
1. α of conductors:
For conductors a is positive. If the temperature of a conductor increases, the average kinetic energy of electrons in the conductor increases. This results in more frequent collisions and hence the resistivity increases. Even though the resistivity of conductors like metals varies linearly for a wide range of temperatures, there also exists a nonlinear region at very low temperatures. The resistivity approaches some finite value as the temperature approaches absolute zero. As the resistance is directly proportional to the resistivity of the material, we can also write the resistance of a conductor at temperature T °C as
RT -R0 = [1 + α(T -T0)] ……. (2)
The temperature coefficient can be also be obtained from the equation (2), +

where ∆R = RT -R0 changes in resistance during the change in temperature ∆T = T – T0
2. α of semiconductors:
For semiconductors, the resistivity decreases with an increase in temperature. As the temperature increases, more electrons will be liberated from their atoms (Refer to unit 9 for conduction in semi-conductors). Hence the current increases and therefore the resistivity decreases. A semiconductor with a negative temperature coefficient of resistance is called a thermistor.
We can understand the temperature dependence of resistivity in the following way. The electrical conductivity, σ = \(\frac{n e^{2} \tau}{m}\) \(\frac{m}{n e^{2} \tau}\). As the resistivity is inverse of σ, it can be written as,
σ = \(\frac{n e^{2} \tau}{m}\) \(\frac{m}{n e^{2} \tau}\) …… (4)
The resistivity of materials is
- inversely proportional to the number density (n) of the electrons
- inversely proportional to the average time between the collisions (τ).
In metals, if the temperature increases, the average time between the collision (τ) decreases and n is independent of temperature. In semiconductors when temperature increases, n increases, and τ decreases, but an increase in n is dominant than decreasing x, so that overall resistivity decreases.
Question 3.
Explain the effective internal resistance of cells connected in series combination. Compare the results to the external resistance.
Answer:
Cells in series Several cells can be connected to form a battery. In a series connection, the negative terminal of one cell is connected to the positive terminal of the second cell, the negative terminal of the second cell is connected to the positive terminal of the third cell and so on. The free positive terminal of the first cell and the free negative terminal of the last cell become the terminals of the battery.

Suppose n cells, each of emf ξ volts and internal resistance r ohms are connected in series with an external resistance R.
The total emf of the battery = nξ
The total resistance in the circuit = nr + R
By Ohm’s law, the current in the circuit is

Case (a) If r << R, then,
I = \(\frac { nξ }{ R }\)nI1 ≈ nI1 ……. (2)
where, I, is the current due to a single cell \(\left(\mathrm{I}_{1}=\frac{\xi}{\mathrm{R}}\right)\)
Thus, if r is negligible when compared to R the current supplied by the battery is n times that supplied by a single cell.
Case (b) If r >> R, I = \(\frac { nξ }{ nr }\) ≈ \(\frac { ξ }{ R }\) …….. (3)
It is the current due to a single cell. That is, current due to the whole battery is the same as that due to a single cell and hence there is no advantage in connecting several cells. Thus the series connection of cells is advantageous only when the effective internal resistance of the cells is negligibly small compared with R.
Question 4.
Explain the effective internal resistance of cells connected in parallel combination. Compare the results to the external resistance.
Answer:
Cells in parallel: In parallel connection, all the positive terminals of the cells are connected to one point and all the negative terminals to a second point. These two points form the positive and negative terminals of the battery.
Let n cells be connected in parallel between points A and B and a resistance R is connected between points A and B. Let ξ, be the emf and r the internal resistance of each cell.
The equivalent internal resistance of the battery is \(\frac { 1 }{{ r }_{eq}}\) = \(\frac { 1 }{ r }\) + \(\frac { 1 }{ r }\) + ….. \(\frac { 1 }{ r }\) (n terms) = \(\frac { n }{ r }\).
So reg = \(\frac { r }{ n }\) and the total resistance in the circuit = R + \(\frac { r }{ n }\). The total emf is the potential difference between the points A and B, which is equal to ξ. The current in the circuit is given by
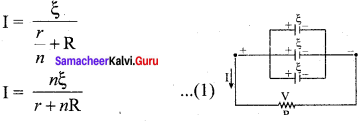
Case (a) If r << R, then,
I = \(\frac { nξ }{ R }\) = nI1 …….. (2)
where II is the current due to a single cell and is equal to \(\frac { ξ }{ R }\) when R is negligible. Thus, the
current through the external resistance due to the whole battery is n times the current due to a single cell.
Case (b) If r << R. I = \(\frac { ξ }{ R }\) …… (3)
The above equation implies that the current due to the whole battery is the same as that due to a single cell. Hence it is advantageous to connect cells in parallel when the external resistance is very small compared to the internal resistance of the cells.
Samacheer Kalvi 12th Physics Current Electricity Numerical Problems
Question 1.
Show that one ampere is equivalent to a flow of 6.25 x 1018 elementary charges per second.
Solution:
Here I = 1 A, t= 1s, e = 1.6 x 10-19 C
As I = \(\frac { q }{ t }\) = \(\frac { ne }{ t }\)
Number of electrons, n = \(\frac { It }{ e }\) = \(\frac { 1 × 1 }{{ 1.6 × 10 }^{19}}\) = 6.25 × 1018
![]()
Question 2.
Calculate the resistivity of a material of a wire 10 m long. 0.4 mm in diameter and having a resistance of 2.0 Ω.
Solution:
Here l = 10 cm, r = 0.2 mm = 0.2 x 10-3 m, R = 2 Ω
\(\left[ r\quad =\quad \frac { d }{ 2 } \right] \)
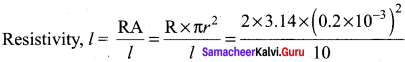
= 2.513 x 10-8 Ω.
Question 3.
A wire of 10 ohm resistance is stretched to thrice its original length. What will be its (i) new resistivity and (ii) new resistance?
Solution:
(i) Resistivity p remains unchanged because it is the property of the material of the wire.
(ii) In both cases, volume of wire is same, so

Question 4.
A copper wire has a resistance of 10 Ω. and an area of cross-section 1 mm2. A potential difference of 10 V exists across the wire. Calculate the drift speed of electrons if the number of electrons per cubic metre in copper is 8 x 1028 electrons.
Solution:
Here, R = 10 Ω, A = 1 mm2 = 10-6 m2, V = 10 V, n = 8 x 1028 electrons/m3
Now,
I = enAvd
∴ \(\frac { V }{ R }\) = enAvd (or) vd = \(\frac { V }{ enAR }\)
= \(\frac{10}{1.6 \times 10^{-19} \times 8 \times 10^{28} \times 10^{-6} \times 10}\) = 0.078 x 10-3 ms-1
= 0.078 x ms-1
Question 5.
(i) At what temperature would the resistance of a copper conductor be double its resistance at 0°C.
(ii) Does this temperature hold for all copper conductors regardless of shape and size? Given a for Cu = 3.9 x 10-3 °C-1.
Solution:
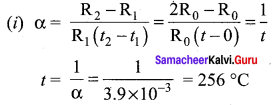
Thus the resistance of copper conductor becomes double at 256 °C.
(ii) Since a does not depend on size and shape of the conductor. So the above result holds for all copper conductors.
Question 6.
Find the value of current I in the circuit shown in the figure.
Solution:
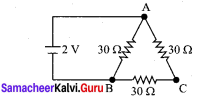
In the circuit, the resistance of arm ACB (30 + 30 = 60 Ω) is parallel with the resistance of arm AB (= 30 Ω).
Hence, the effective resistance of the circuit is
R = \(\frac { 30 × 60 }{ 30 + 60 }\) = 20 Ω
Current, I = \(\frac { V }{ R }\) = \(\frac { 2 }{ 20 }\) = 0.1 A.
Common Errors and Its Rectifications:
Common Errors:
- Sometimes students think that charge and current are the same.
- In doing the calculation part students can’t give the importance to mention the units.
- They may confuse the parallel and series network of the resistance.
Rectifications:
- Charge q = ne Current I = q/t
- Unit is very important to every physical quantity.
- If the resistors are series, their resultant is the sum of all the reciprocal of individual resistance.
- If the resistors are parallel their resultant is the sum of the individual resistances.