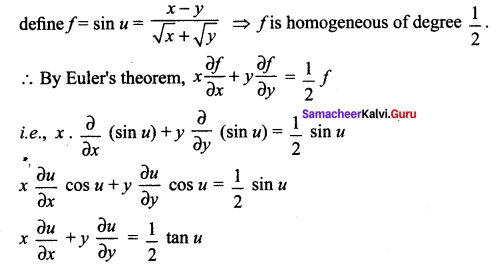You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.7
Question 1.
In each of the following cases, determine whether the following function is homogeneous or not. If it is so, find the degree.

Solution:
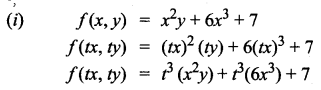
It is not a homogeneous function
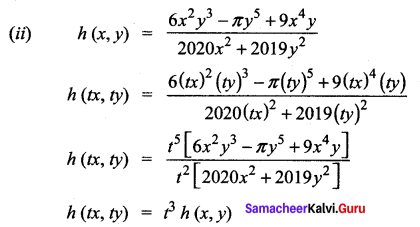
∴ It is a homogeneous function with degree 3.
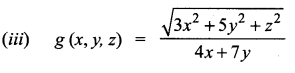
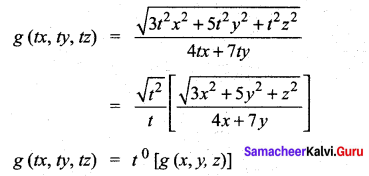
∴ It is homogeneous function of degree 0.
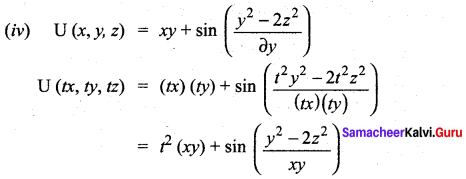
∴ It is not a homogeneous function
![]()
Question 2.
Prove that f(x, y) = x3 – 2x2 y + 3xy2 + y3 is homogeneous; what is the degree? Verify Euler’s Theorem for f.
Solution:
f (x, y) = x3 – 2x2y + 3xy2 + y3
f(tx, ty) = t3x3 – 2(t2x2)(ty) + 3(tx)(t2y2) + t3y3
= t3 [x3 – 2x2y + 3xy2 + y3]
f(tx, ty) = t3 f(x, y)
‘f’ is a homogeneous function of degree 3. By Euler’s theorem, we have

∴ Euler’s Theorem verified
Question 3.
Prove that g(x, y) = x log (\(\frac{y}{x}\)) is homogeneous; what is the degree? Verify Euler’s Theorem for g.
Solution:
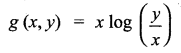

∴ Euler’s Theorem verified
![]()
Question 4.
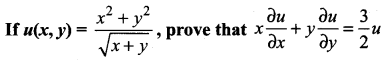
Solution:

Question 5.
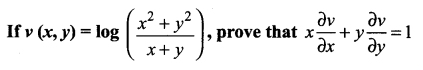
Solution:
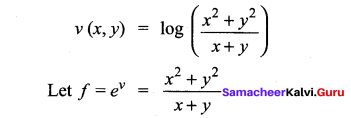
∴ ‘f’ is a homogeneous function of degree 1. By Euler’s theorem, we have

Question 6.
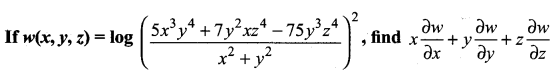
Solution:

![]()
Samacheer Kalvi 12th Maths Solutions Chapter 8 Differentials and Partial Derivatives Ex 8.7 Additional Problems
Question 1.

Solution:
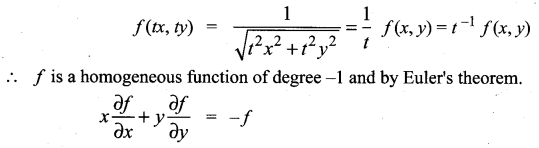
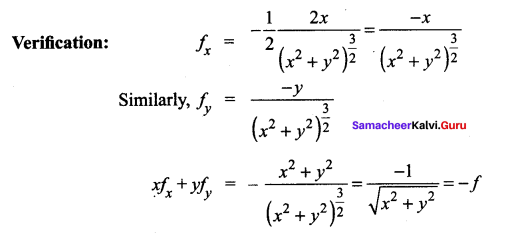
![]()
Question 2.
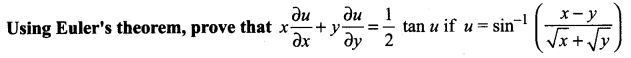
Solution:
R.H.S. is not a homogeneous and hence