You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.3
Queston 1.
Explain why Rolle’s theorem is not applicable to the following functions in the respective intervals.
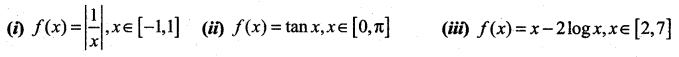
Solution:

f(x) is not continuous at x = 0. So Rolle’s Theorem is not applicable.
(ii) f(x) = tan x, x ∈ [0, π]
The function tan x is not continuous on [0, π] because it is not defined at \(\frac { π }{ 2 }\)
The function is not differentiable on (0, π), because it is not continuous at \(\frac { π }{ 2 }\)
and f(0) = tan (0) = 0
f(π) = tan π = 0
f (0) = f(π) = 0
Since ‘tan x’ is not continuous in [0, π] and not differentiable in (o, π), Rolle’s theorem is not applicable.
(iii) f(x) = x – 2 log x, x ∈ [2, 7]
f(x) is continuous on [2, 7] and
f(x) is differentiable on (2, 7)
f(2) = 2 – 2 log 2, f (7) = 7 – 2 log 7
f(2) ≠ f(7)
Hence, Rolle’s theorem is not applicable.
Question 2.
Using Rolle’s theorem, determine the values of x at which the tangent is parallel to the x-axis for the following functions:

Solution:
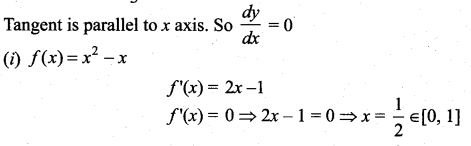
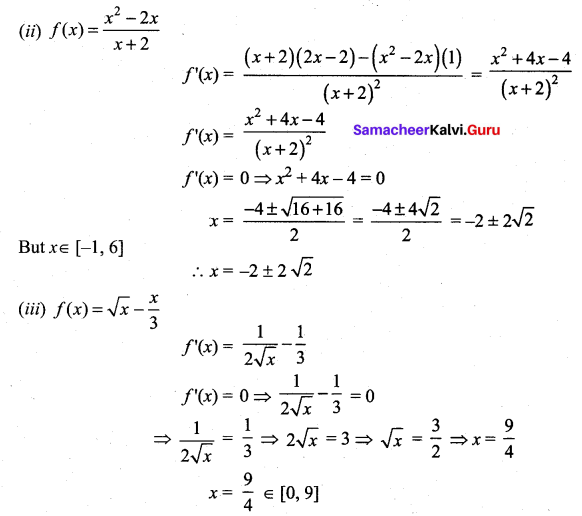
![]()
Question 3.
Explain why Lagrange’s mean value theorem is not applicable to the following functions in the respective intervals :

Solution:
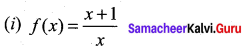
The function is not continuous at x = 0. So Lagrange’s mean value theorem is not applicable in the given interval.
(ii) f(x) = |3x + 1|, x ∈ [-1, 3]
3x + 1 = 0
x = –\(\frac { 1 }{ 3 }\)
f(x) is not differentiable at x = –\(\frac { 1 }{ 3 }\)
Hence, Lagrange’s mean value theorem is not applicable.
Question 4.
Using the Lagrange’s mean value theorem determine the values of x at which the tangent is parallel to the secant line at the end points of the given interval:
(i) f(x) = x3 – 3x + 2, x ∈ [-2, 2]
(ii) f(x) = (x – 2)(x – 7), x ∈ [3, 11]
Solution:
(i) f(x) = x3 – 3x + 2
Here a = -2, b = 2

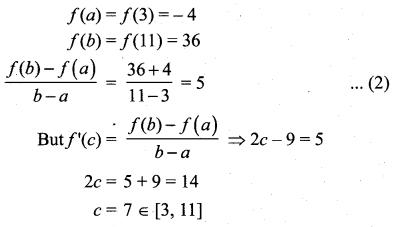
Question 5.
Show that the value in the conclusion of the mean value theorem for

Solution:
(i) 
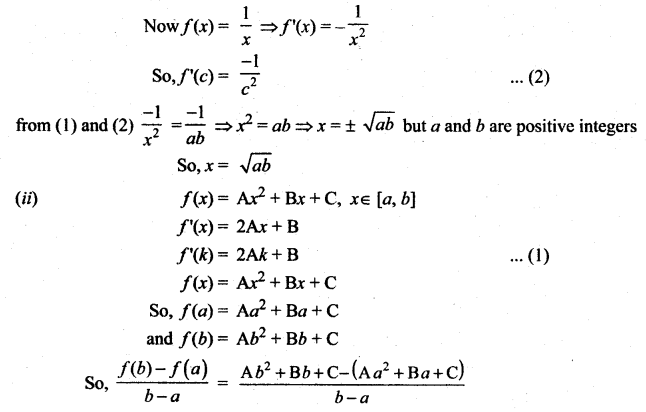
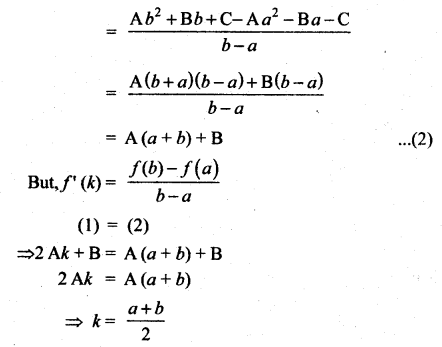
Question 6.
A racecar driver is racing at 20th km. If his speed never exceeds 150 km/hr, what is the maximum distance he can cover in the next two hours?
Solution:
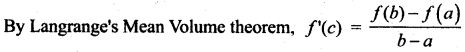
Here the interval is [0, 2] and f(0) = 20, f(2) = ?
f(b) – f(a) ≤ (b – a)f’c)
here f (a) = 20
⇒ f(b) – 20 ≤ 150(2 – 0)
⇒ f(b) ≤ 320
(i.e) f(2) = 320 km.
![]()
Question 7.
Suppose that for a function f(x), f'(x) ≤ 1 for all 1 ≤ x ≤ 4. Show that f(4) – f(1) ≤ 3.
Solution:
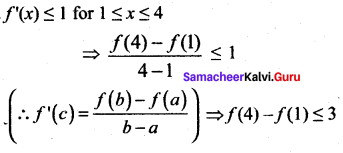
Question 8.
Does there exist a differentiable function f(x) such that f(0) = -1, f(2) = 4 and f'(x) ≤ 2 for all x. Justify your answer.
Solution:
f(0) = -1, f(2) = 4, f(x) ≤ 2
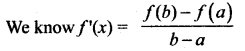
Here a = 0, b = 2
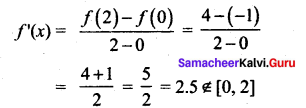
So this is not possible
Question 9.
Show that there lies a point on the curve 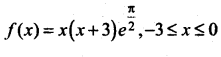 where the tangent is drawn is parallel to the x-axis.
where the tangent is drawn is parallel to the x-axis.
Solution:
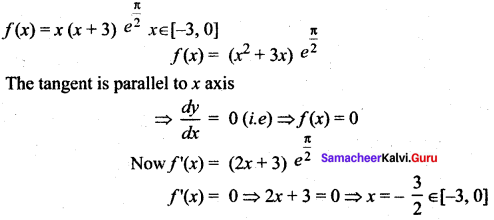
⇒ There lies a point in [-3,0], where the tangent is parallel to the x-axis.
Question 10.
Using mean value theorem prove that for, a > 0, b > 0, |e-a – e-b| < |a – b|
Solution:
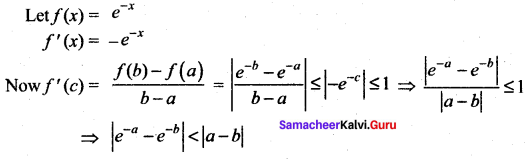
Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.3 Additional Questions Solved
Question 1.
Verify Rolle’s theorem for the following:
(i) f(x) = x3 – 3x + 3, 0 ≤ x ≤ 1
(ii) f(x) = tan x, 0 ≤ x ≤ π
(iii) f(x) = | x |, – 1 ≤ x ≤ 1
(iv) f (x) = sin2 x, 0 ≤ x ≤ π
(v) f(x) = ex sin x, 0 ≤ x ≤ π
(vi) f(x) = x(x – 1) (x – 2), 0 ≤ x ≤ 2
Solution:
(i) f(x) = x3 – 3x + 3, 0 ≤ x ≤ 1. f is continuous on [0, 1] and differentiable in (0, 1)
f(0) = 3 and f(1) = 1 ∴ f(a) ≠ f(b)
∴ Rolle’s theorem, does not hold, since f(a) = f(b) is not satisfied.
Also note that f’ (x) = 3x2 – 3 = 0 ⇒ x2 = 1 ⇒ x = ±1
There exists no point c ∈ (0, 1) satisfying f’ (c) = 0.
(ii) f(x) = tan x, 0 ≤ x ≤ π.
f ‘(x) is not continuous in [0, π] as tan x tends to + ∞ at x = \(\frac{\pi}{2}\),
∴ Rolle’s theorem is not applicable.
(iii) f (x) = | x |, -1 ≤ x ≤ 1
f is continuous in [-1, 1] but not differentiable in (-1, 1) since f'(0) does not exist.
∴ Rolle’s theorem is not applicable.
(iv) f (x) = sin2x, 0 ≤ x ≤ π
f is continuous in [0, π] and differentiable in (0, π). f(0) = f(π) = 0
(i.e.,) f satisfies hypothesis of Rolle’s theorem.
f’ (x) = 2 sin x cos x = sin 2x
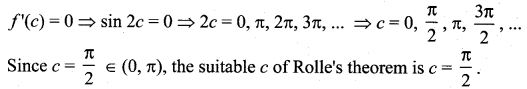
(v) f(x) = ex, sin x, 0 ≤ x ≤ π
ex and sin x are continuous for all x, therefore the product ex sin x is continuous in 0 ≤ x ≤ π.
f’ (x) = ex sin x + ex cos x = ex (sin x + cos x) exist in 0 < x < π ⇒ f'(x) is differentiable in (0, π)
f (0) = e° sin 0 = 0
f (π) = eπ sin π = 0
∴ f satisfies hypothesis of Rolle’s theorem.
Thus there exists c ∈ (0, π) satisfying f'(c) = 0 ⇒ ec (sin c + cos c) = 0
⇒ ec = 0 or sin c + cos c = 0
⇒ ec = 0 ⇒ c = -∞ which is not meaningful here.
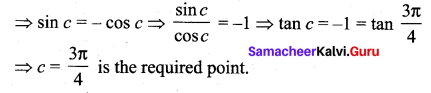
(vi) f(x) = x (x – 1) (x – 2), 0 ≤ x ≤ 2
f is not continuous in [0, 2] and differentiable in (0, 2)
f(0) = 0 = f(2), satisfying hypothesis of Rolle’s theorem.
Now f'(x) = (x – 1) (x – 2) + x(x – 2) + x(x – 1) = 0
Note: There could exist more than one such ‘c’ appearing in the statement of Rolle’s theorem.
![]()
Question 2.
Suppose that f(0) = -3 and f'(x) ≤ 5 for all values of x, how large can f(2) possibly be?
Solution:
Since by hypothesis f is differentiable, f is continuous everywhere. We can apply Lagrange’s Law of the mean on the interval [0, 2], There exist atleast one ‘c’ ∈ (0, 2) such that
f(2) – f(0) = f'(c)(2 – 0)
f(2) = f(0) + 2f'(c) = -3 + 2f'(c)
Given that f'(x) ≤ 5 for all x.
In particular we know that f'(c) ≤ 5. Multiplying both sides of the inequality by 2, we have
2f'(c) ≤ 10
f(2) = -3 + 2f'(c) < -3 + 10 = 7
i.e., the largest possible value of f(2) is 7.
Question 3.
Using Rolle’s theorem find the points on the curves = x2 +1, -2 ≤ x ≤ 2 where the tangent is parallel to X-axis
Solution:
![]()
a = -2,
b = 2
f(x) = x2 + 1
f(a) = f(-2) = 4 + 1 = 5
f(b) = f(2) = 4 + 1 = 5
So, f(a) = f(b)
f'(x) = 2x
f'(x) = 0 ⇒ 2x = 0
x = 0 where 0 ∈ (-2, 2)
at x = 0, y = 0 + 1 = 1
So, the point is (0, 1) at (0, 1) the tangent drawn is parallel to X-axis
Question 4.
Find ‘C’ of Lagrange’s mean value theorem for the function f(x) = 2x3 + x2 – x – 1, [0, 2]
Solution:
f(x) = 2x3 + x2 – x – 1
a = 0,
b = 2
f(a) = f(0) = -1
f(b) = f(2) = 2(8) = 4 – 2 – 1 = 16 + 4 – 2 – 1 = 17
By Lagrange’s mean value theorem, we get a constant c ∈ (a, b) such that

![]()
Question 5.
Find ‘C’ of Lagrange’s mean value theorem for the function f(x) = x3 + x2 – 3x in [1, 3]
Solution:
f(x) = x3 + x2 – 3x
a = 1,
b=3
f(a) = f(1) = 1 – 5 – 3 = -7
f(b) = f(3) = 27 – 5(9) – 3(3)
= 27 – 45 – 9 = -27
f'(x) = 3x2 – 10x – 3
f'(x) = 3c2 – 10c – 3
From (1) and (2),
3c2 – 10c – 3 = -10
3c2 – 10c – 3 + 10 = 0
3c2 – 10c + 7 = 0
3c2 – 3c – 7c + 7 = 0
So, Lagrange’s mean value theorem is true with c = \(\frac{7}{3}\)