You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 7 Applications of Differential Calculus Ex 7.9
Question 1.
Find the asymptotes of the following curves:
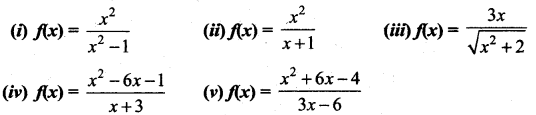
Solution:

y = 1 is a horizontal asymptote
So the asymptotes are x = -1, x = +1, y = 1
![]()
(ii) Since the numerator is of higher degree than the denominator we have a slant asymptote to find that asymptote we have to divide the numerator by the denominator So the slant asymptote is y = x – 1
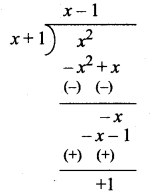
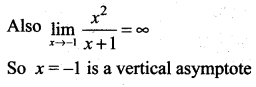

∴ y = 3 and y = -3 are the horizontal asymptotes and there is no slant asymptote
(iv) Since the numerator is of highest degree than the denominator. We have a slant asymptote to find it we have to divide numerator by the denominator.
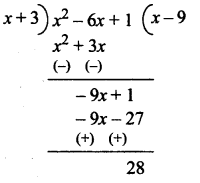
So the equation of asymptotes is y = x – 9 and x = -3
(v) Since the numerator is of the highest degree than the denominator.
We have a slant asymptote to find it we have to divide the numerator by the denominator.
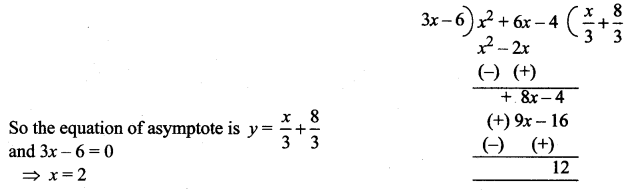
![]()
Question 2.
Sketch the graphs of the following functions:
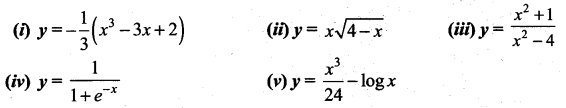
Solution:
![]()
Factorizing we get
![]()
• The domain and the range of the given function f(x) are the entire real line.
• Putting y = 0 we get x = 1, 1, -2.
Hence the x intercepts are (1, 0) and (-2, 0) and by putting x = 0 we get y = \(-\frac{2}{3}\)
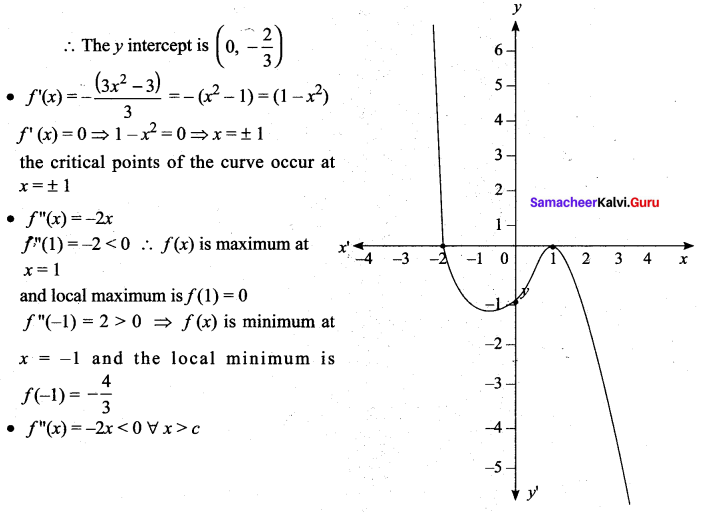
∴ The function is concave upward in the negative real line.
• Since f”(x) = 0 at x = 0 and f”(x) changes its sign when passing through x = 0, x = 0 is a point of inflection is \(\left(0,-\frac{2}{3}\right)\)
• The curve has no asymptotes.
(ii)
![]()
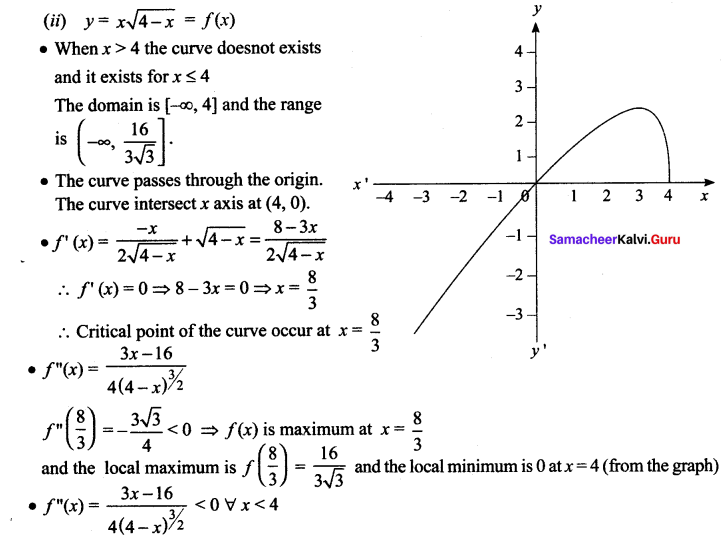
The curve concave downward in the negative real line
• No point of inflection exists.
• as x ➝ ∞, y = ± ∞ and so the curve does not have any asymptotes
(iii)
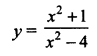
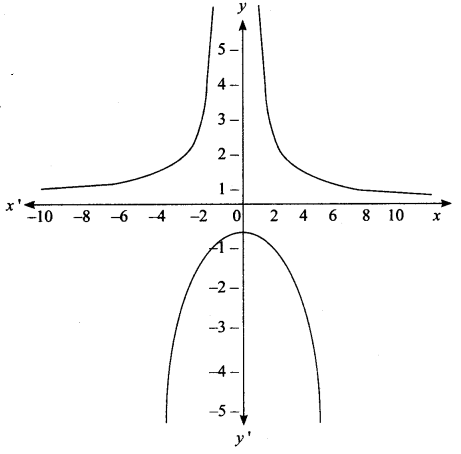

• Putting y = 0. x is unreal hence there is no ‘x’ intercept. By putting x = 0 we get

• No points of reflection
• When x = ± 2, y = ∞, Vertical asymptotes are x = 2 and x = -2 and horizontal asymptote is y = 1
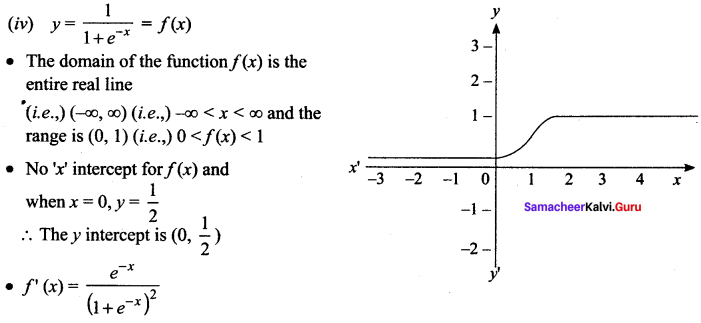
f'(x) = 0 ⇒ e-x = 0 which is not possible hence there is no extremum.
• No vertical asymptote for the curve and the horizontal asymptotes are y = 1 and y = 0
![]()
(v)
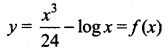
• The curve exists only for positive values of (x > 0)


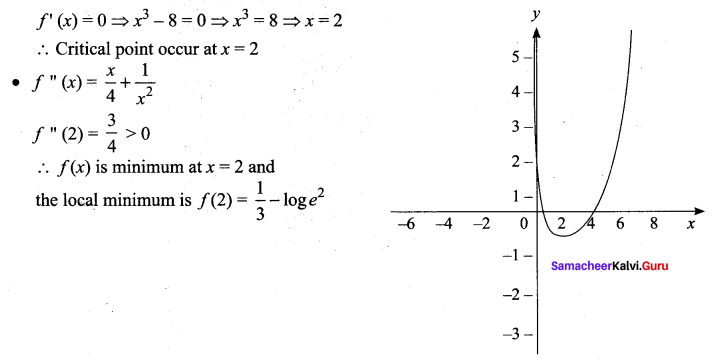
• No point of inflection.
• No horizontal asymptote is possible.
But the vertical asymptote is x = 0(y-axis).