Students can Download Tamil Nadu 12th Maths Model Question Paper 2 English Medium Pdf, Tamil Nadu 12th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
TN State Board 12th Maths Model Question Paper 2 English Medium
Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- questions of Part I, II. III and IV are to be attempted separately
- Question numbers 1 to 20 in Pan I are objective type questions of one -mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
- Question numbers 21 to 30 in Part II are two-marks questions. These are to be answered in about one or two sentences.
- Question numbers 31 to 40 in Parr III are three-marks questions, These are to be answered in about three to five short sentences.
- Question numbers 41 to 47 in Part IV are five-marks questions. These are to be answered) in detail. Draw diagrams wherever necessary.
Time: 3 Hours
Maximum Marks: 90
Part-I
I. Choose the correct answer. Answer all the questions. [20 × 1 = 20]
Question 1.
If A = \(\left[\begin{array}{ll}
7 & 3 \\
4 & 2
\end{array}\right]\) then 9I2 – A =
(a) A-1
(b) \(\frac{A^{-1}}{2}\)
(c) 3A-1
(d) 2A-1
Answer:
(d) 2A-1
Question 2.
If (1+ i) (1+ 2i) (1+ 3i)…(1+ ni) = x + iy, then 2-5T0…(1 + n2 ) is ..
(a) 1
(b) i
(c) x2 + y2
(d) 1 + n2
Answer:
(c) x2 + y2
Question 3.
If p + iq = (2 – 3i) (4 + 2i) then q is
(a) 14
(b) -14
(c) -8
(d) 8
Answer:
(c) -8
![]()
Question 4.
A zero of x3 + 64 is
(a) 0
(b) 4
(c) 4i
(d) -4
Answer:
(d) -4
Question 5.
sin-1(2COS2A – 1) + cos-1(1 – 2 sin2x) = .

(a) π/2
(b) π /3
(c) π/4
(d) π/6
Answer:
(a) π/2
Question 6.
If cot-1 x = \(\frac{2 \pi}{5}\) for some x ∈ R, the value of tan-1 x is
(a) \(-\frac{\pi}{10}\)
(b) \(\frac{\pi}{5}\)
(c) \(\frac{\pi}{10}\)
(d) \(-\frac{\pi}{5}\)
Answer:
(c) \(\frac{\pi}{10}\)
Question 7.
An ellipse has OB as semi minor axes, F and F’ its foci and the angle FBF’ is a right angle. Then the eccentricity of the ellipse is

Answer:
(a) \(\frac{1}{\sqrt{2}}\)
Question 8.
The focus of the parabola x2 = 20 y is
(a) (0, 0)
(b) (5, 0)
(c) (0, 5)
(d) (-5, 0)
Answer:
(c) (0, 5)
![]()
Question 9.
If the planes \(\vec{r} \cdot(2 \hat{i}-\lambda \hat{j}+\hat{k})=3\) and \((4 \hat{i}+\hat{j}-\mu \hat{k})=5\) are parallel, then the value of λ and μ are

Answer:
(c) \(-\frac{1}{2}\) , -2
Question 10.
The unit normal vectors to the plane 2x – y + 2z = 5 are

Question 11.
The slope of the line normal to the curve f(x) – 2cos 4x at x = \(\frac{\pi}{2}\) is ……………….
(a) -4√3
(b) -4
(c) √3/12
(d) 4√3
Answer:
(c) √3/12
Question 12.
The curve y2 = x2 ( 1 – x) has
(a) only one loop between x = -1 and x = 0
(b) only one loop between x = 0 and x = 1
(c) two loops between x = -1 and x = 1
(d) no loop
Answer:
(b) only one loop between x = 0 and x = 1
Question 13.
If w (x, y) = xy, x > 0, then \(\frac{\partial w}{\partial x}\) is equal to
(a) xy logx
(b) y logx
(c) yxy-1
(d) xlogy
Answer:
(c) yxy-1
Question 14.
If (x, y, z) = xy + yz + zx, then fx – fz is equal to
(a) z – x
(b) y – z
(c) x – z
(d) y – x
Answer:
(a) z – x
Question 15.
If \(\frac{\Gamma(n+2)}{\Gamma(n)}\) = 90 then n is
(a) 10
(b) 5
(c) 8
(d) 9
Answer:
(d) 9
![]()
Question 16.
If n is even then \(\int_{0}^{\pi / 2} \sin ^{n} x d x\) is ………………

Answer:
(b) 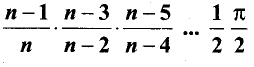
Question 17.
The slope at any point of a curve y =/(x) is given by \(\frac{d y}{d x}=3 x^{2}\) and it passes through (-1,1).
Then the equation of the curve is
(a) y = x3 + 2
(b) y = 3x2 + 4
(c) y = 3x3 + 4
(d) y = x3 + 5
Answer:
(a) y = x3 + 2
Question 18.
The solution of the differential equation \(\frac{d y}{d x}+\frac{1}{\sqrt{1-x^{2}}}=0\) is
(a) y + sin-1x = c
(b) x + sin-1y = 0
(c) y2 + 2sin-1x = c
(d) x2 + 2sin-1y = 0
Question 19.
Suppose that x takes on one of the values 0, 1, and 2. If for some constant k,
P(X = i) = k P(x = i – 1) for i = 1, 2 P(x = 0) = 1/7. Then the value of k is
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2
Question 20.
Determine the truth value of each of the following statements:
(a) 4 + 2 = 5 and 6 + 3 = 9
(b) 3 + 2 = 5 and 6 + 1 = 7
(c) 4 + 5 = 9 and 1 + 2 = 4
(d) 3 + 2 = 5 and4 + 7 = 11
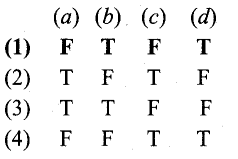
Answer:
(1) (a) F
(b) T
(c) F
(d) T
Part – II
II. Answer any seven questions. Question No. 30 is compulsory. [7 × 2 = 14]
Question 21.
If A = \(\left[\begin{array}{ll}
4 & 3 \\
2 & 5
\end{array}\right]\) , find x and y such that A2 + xA + yI2 = O2. Hence , find A-1
Answer:
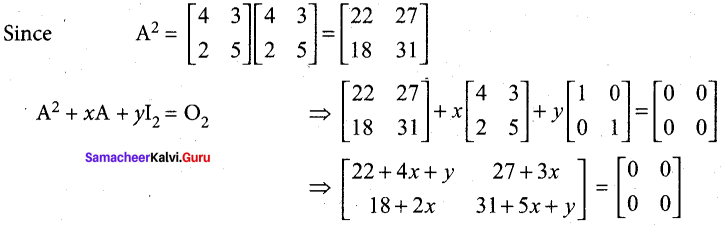
So, we get 22 + 4x + y = 0, 31+ 5x + y – 0, 27 + 3x = 0 and 18 + 2x = 0.
Hence x = -9 and y = 14. Then, we get A2 – 9A + 14I2 = O2
Post-multiplying this equation by A-1, we get A – 9I + 14A-1 – I2 = O2. Hence, we get
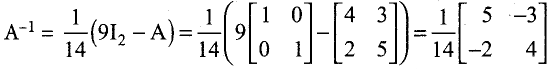
![]()
Question 22.
Find the principal argument arg z, when z = \(\frac{-2}{1+i \sqrt{3}}\)
Answer:
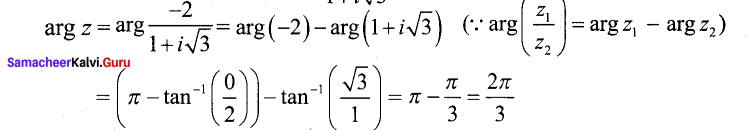
This implies that one of the values of arg z is \(\frac{2 \pi}{3}\)
Since \(\frac{2 \pi}{3}\) lies between -π and π , the principal argument arg z is \(\frac{2 \pi}{3}\)
Question 23.
Verify whether the line \(\frac{x-3}{-4}=\frac{y-4}{-7}=\frac{z+3}{12}\) lies in the plane 5x – y + z = 8 .
Answer:
Here, (x1, y1, z1) = (3,4, -3) and direction ratios of the given straight line are (a, b, c) – (-4, -7,12).
Direction ratios of the normal to the given plane are (A, B, C) = (5, -1,1).
We observe that, the given point (x1, y1, z1) = (3,4, -3) satisfies the given plane 5x – y + z = 8
Next, aA+ bB + cC = (-4)(5) + (-7)(-l) + (12)( 1) = -1 ≠ 0. So, the normal to the plane is not perpendicular to the line. Hence, the given line does not lie in the plane.
Question 24.
Evaluate \(\begin{aligned}
&\lim\\
&x \rightarrow 0^{+} \quad x^{2} \log e^{x}
\end{aligned}\)
Answer:
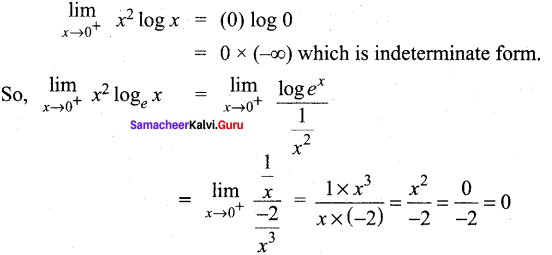
Question 25.
Find a linear approximation for the function at the indicated points.
g(x) = \(\sqrt{x^{2}+9}\), x0 = -4
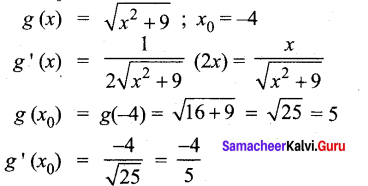
The required linear approximation L(x) = g (x0) + g’ (x0) (x – x0)
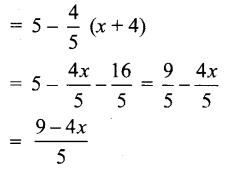
Question 26.
Evaluate: \(\int_{0}^{2 \pi} x^{2} \sin n x d x\) , Where n is a positive integer.
Answer:
Taking u = x2 and v = sin nx, and applying the Bernoulli’s formula, we get
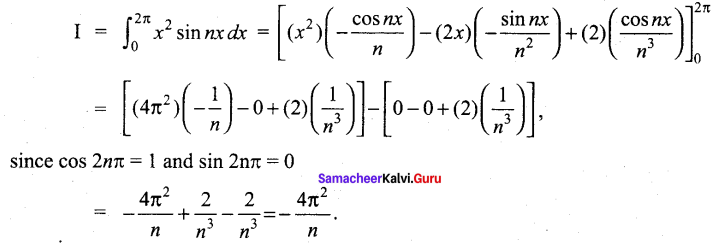
Question 27.
Form the differential equation from the equation y2 = 4a (x – a)
Answer:
y2= 4 a(x-a) …(1)
Differentiating, 2yy’ = 4a …(2)
Eliminating a between (1) and (2) we get
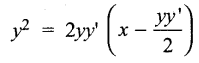
(yy ‘)2 – 2xyy’ + y2 = 0
Question 28.
Compute P(X = k) for the binomial distribution, B(n,p) where n = 6, p = 1/3, k = 3
Answer:
Given n = 6, p = 1/3,k = 3
∴ q = 1 – p = \(1-\frac{1}{3}=\frac{2}{3}\)
P(X = x) = nCxpxqn-x, x = 0, 1,2,…………n
P (X = k) = P (X = 3)
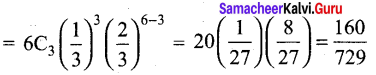
Question 29.
Let A = {a + √5b : a, b∈Z} . Check whether the usual multiplication is a binary operation on A.
Answer:
Let A = a + √5 b and B = c + √5 d, where a, b,c,d∈ R.
Now A * B = (a + √5 b) (c + √5 d)
= ac + √5 ad + √5 bc + √5 b √5 d
= (ac + 5 bd) + 45 (ad + bc) ∈ A .
Where a, b,c,d ∈ Z.
So * is a binary operation.
Question 30.
Find the value of \(\sin ^{-1}\left(\sin \frac{5 \pi}{9} \cos \frac{\pi}{9}+\cos \frac{5 \pi}{9} s \quad \frac{\pi}{9}\right)\)
Answer:
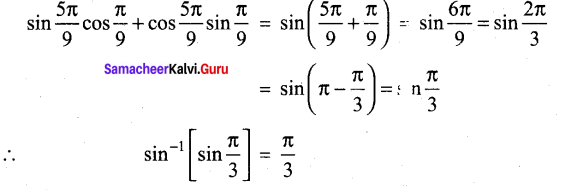
Part – III
III. Answer any seven questions. Question No. 40 is compulsory. [7 x 3 = 21]
Question 31.
Solve the following system of linear equations, using matrix inversion method:
5x + 2y – 3, 3x + 2y – 5.
Answer:
The matrix form of the system is AX = B, where A :\(\left[\begin{array}{ll}
5 & 2 \\
3 & 2
\end{array}\right]\) , X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\), B = \(\left[\begin{array}{l}
3 \\
5
\end{array}\right]\)
We find |A| = \(\left|\begin{array}{ll}
5 & 2 \\
3 & 2
\end{array}\right|\) = 10 – 6 = 4 ≠ 0
So A-1 exists A-1 = \(\frac{1}{4}\left[\begin{array}{rr}
2 & -2 \\
-3 & 5
\end{array}\right]\)
Then, applying the formula X = A 1B, we get
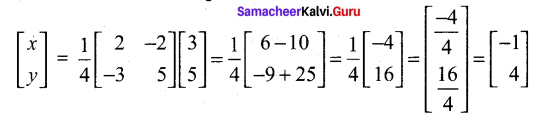
So the solution is (x = -1 ,y = 4).
Question 32.
If z1 = 2 – i and z2 = -4 + 3i, find the inverse of z1 z2 and \(\frac{z_{1}}{z_{2}}\)
Answer:
z1 = 2 – i, z2 = -4 + 3i

Question 33.
If k is real, discuss the nature of the roots of the polynomial equation 2x2 + kx + k = 0, in terms of k.
Answer:
The given quadratic equation is 2x2 + kx + k = 0
a = 2,b = k,c = k
∆ = b2 – 4ac = k2 – 4(2) k = k2 – 8k
(i) If the roots are equal
k2 – 8k = 0 ⇒ k(k -8) = 0
k = 0, k = 8
(it) If the roots are real
k2 – 8k > 0
k (k – 8) > 0
k ∈ (-∞, 0) ∪ (8, ∞)
(iii) ‘If this roots are imaginary
k2 – 8k < 0 ⇒ f ∈ (0, 8)
Question 34.
Find the number of solution of the equation tan-1 (x – 1) + tan-1 x + tan-1 (x + 1) = tan-1(3x).
Answer:
tan-1(x – 1) + tan-1x + tan-1(x + 1) = tan-1(3x)
tan-1(x – 1) + tan-1(x + 1) = tan-1 3x – tan-1 x

So, the equation has 2 solutions.
![]()
Question 35.
Find the non-parametric form of vector equation, and Cartesian equations of the plane \(\vec{r}=(6 \hat{i}-\hat{j}+\hat{k})+s(-\hat{i}+2 \hat{j}+\hat{k})+t(-5 \hat{i}-4 \hat{j}-5 \hat{k})\)
Answer:
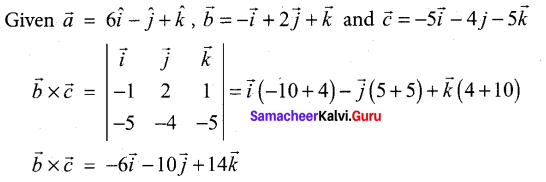
Non-parametric form of vector equation

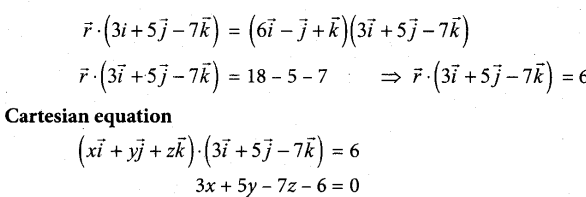
Question 36.
Find two positive numbers whose sum is 12 and their product is maximum.
Answer:
Let the two numbers be x, 12 – x.
Their product p = x (12 – x) – 12x – x2
To find the maximum product.
p’ (x) = 12 – 2x
p”(x) = -2
p’ (x) = 0 ⇒ 12 – 2x = 0 2x = 12 => x = 6
at x = 6, p”(x) = -2 = -ve
⇒ p is maximum at x = 6
when x = 6, 12-x = 12 – 6 = 6
So the two numbers are 6, 6
Question 37.
Find the differential equation that will represent family of all circles having centres on the x-axis and the radius is unity.
Answer:
Equation of a circle with centre on x-axis and radius 1 unit is
(x-a)2 + y2 = 1 …(1)
Differentiating with respect to x,
2 (x-a) + 2yy’ = 0
⇒ 2 (x – a) = – 2yy’
(or) x-a = -yy’ …(2)
Substituting (2) in (1), we get,
(-yy’)2 + y2 = 1
(i.e. y2 (y’)2 + y2 = 1 ⇒ y2 [1 + (y’)2] = 1
Question 38.
The probability that a certain kind of component will survive a electrical test is \(\frac{3}{4}\). Find
the probability that exactly 3 of the 5 components tested survive.
Answer:
Given n = 5
Probability that a component survive in a test =p = \(\frac{3}{4}\)
∴ q = 1 – p = \(1-\frac{3}{4}=\frac{1}{4}\)
Let ‘X’ be the random variable denotes the number of components survived in a test.
Probability of ‘x’ successes in V trials is
P (X = x) = nCxpxqn-x, x = 0, 1,2,………n
Probability that exactly 3 components survive

Question 39.
Fill in the following table so that the binary operation * on A = {a,b,c} is commutative.

Answer:
Given that the binary operation * is Commutative.
To find a * b :
a * b = b * a (∵ * is a Commutative)
Here b * a = c. So a * b = c
To find a * c :
a * c = c * a (∵ * is a Commutative)
c * a = a. (Given)
So a * c = a
To find c * b :
c * b = b * c
Here b * c = a. So c * b = a

Question 40.
Find the area of the region enclosed by y2 = x and y = x – 2.
Answer:
The points of intersection of the parabola y2 = x and the line y = x – 2 are (1, – 1) and (4, 2)
To compute the region [shown in the figure] by integrating with respect to x, we would have to split the region into two parts, because the equation of the lower boundary changes at x = 1. However if we integrate with respect to y no splitting is necessary.
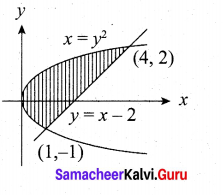

![]()
Part – IV
IV. Answer all the questions. [ 7 x 5 = 35]
Question 41.
(a) Use product \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
0 & 2 & -3 \\
3 & -2 & 4
\end{array}\right]\left[\begin{array}{rrr}
-2 & 0 & 1 \\
9 & 2 & -3 \\
6 & 1 & -2
\end{array}\right]\)
to solve the system of equations x – y + 2z = 1, 2y – 3z = 1, 3x – 2y + 4z = 2.
Answer:

The system of equations can be written in the form AX = C, where

Thus x = 0, y = 5 and z = 3
(b) Find, by integration, the volume of the container which is in the shape of a right circular conical frustum as shown in the Figure.
Answer:

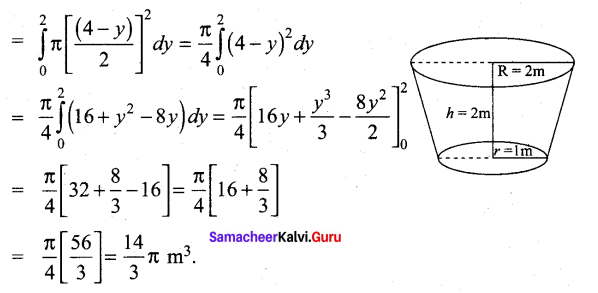
Question 42.
(a) Simplify (-√3 + 3i)31
Answer:
Let – √3 + 3i = r (cos θ + z sin θ). Then, we get
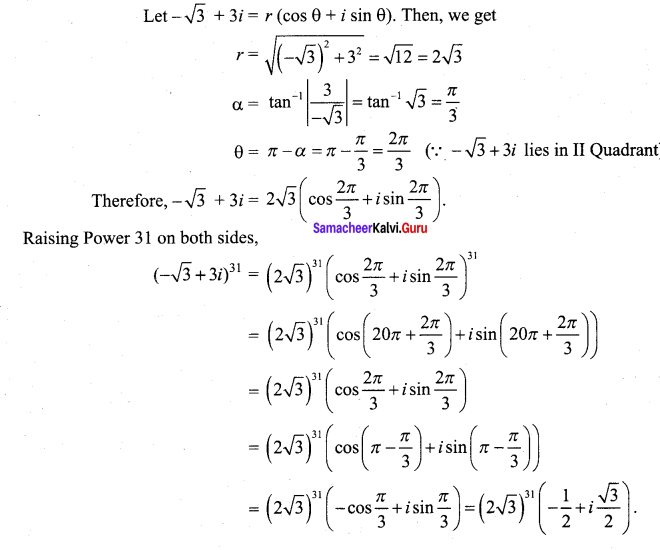
(b) Solve the following equation x4 – 10x3 + 26x2 – 10x + 1 = 0.
Answer:
This equation is Type I even degree reciprocal equation. Hence it can be rewritten as
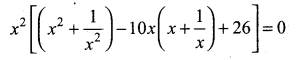
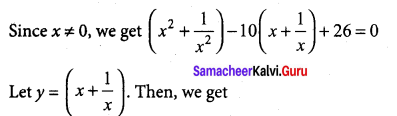
[(y2 – 2) – 10y + 26] = 0 ⇒ (y2 – 10y + 24) = 0 ⇒ (y – 6) {y – 4) = 0 ⇒ y = 6 (or) 4

Hence the roots are 3 ± 2 √2, 2 ± √3
![]()
Question 43.
(a) Solve
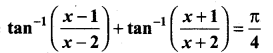
Answer:

(b) Suppose a person deposits 10,000 Indian rupees in a bank account at the rate of 5% per annum compounded continuously. How much money will be in his bank account 18 months later?
Answer:
Let P be the principal
Rate of interest 5 %

Given, when t = 0, P = 10000
⇒ c = 10000
Question 44.
(a) Find the equation of the circle through the points (1, 0), (-1, 0), and (0, 1).
Answer:
Let the required circle be
x2 + y2 + 2gx + 2fy + c = 0 ……(A)
The circle passes through (1, 0), (-1, 0) and (0, 1)
(1,0) ⇒ 1 +0 + 2g(1) + 2f(0) + c = 0 -(A)
2g + c = -1
(-1, 0) ⇒ 1 + 0 + 2g (-1) + 2/(0) + c = 0 …(1)
-2g + c = -1
(0,1)⇒ 0+ 1 +2g(0) + 2f(l) + c = 0 …(2)
2 + c = -1
Now solving (1), (2) and (3) …(3)
2g + c = -1 …(1)
-2g + c = -1 (2)
(1) + (2) ⇒ 2c = -2 ⇒ c = -1
Substituting c = -1 in (1) we get
2g – 1 = -1 2g = -1 + 1= 0 ⇒ g = 0
Substituting c = -1 in (3) we get
2f – 1 = -1 ⇒ 2f = -1 + 1 = 0 ⇒ f = 0
So we get g = 0,f= 0 and c = -1
So the required circle will be
x2 + y2 + 2(0)x + 2(0)y – 1 = 0
(i.e) x2 + y2 – 1 = 0 ⇒ x2 + y2 = 1
[OR]
(b) Find the area of the loop of the curve 3ay2 = x(x – a)2.
Answer:
Put y = 0; we get x = 0, a
It meets the x – axis at x = 0 and x = a
∴ Here a loop is formed between the points (0, 0) and (a, 0) about x-axis. Since the curve is symmetrical about x-axis, the area of the loop is twice the area of the portion above the x – axis.

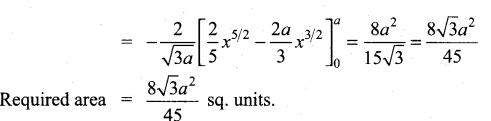
Question 45.
Show that the lines \(\frac{x-3}{3}=\frac{y-3}{-1}, z-1=0\) and \(\frac{x-6}{2}=\frac{z-1}{3}, y-2=0\) interest. Also find the point of intersection.
Answer:
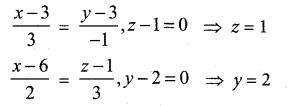
(x1, y1, z1) = (3, 3,1) and (x2, y2, z2) = (6,2,1)
(b1 b2, b3) = (3, -1, 0) and (d1 d2, d3) = (2, 0, 3)
Condition for intersection of two lines

Given two lines are intersecting lines.
Any point on the first line
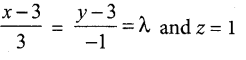
(3λ + 3, -λ + 3,1)
Any point on the Second line
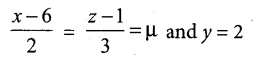
(2µ + 6, 2, 3µ + 1)
∴ 3µ + 1 = 1
3µ = 0
µ = 0
-λ + 3 = 2
-λ = -1
λ = 1
∴ The required point of intersection is (6, 2, 1)
(b) Prove that \(p \rightarrow(\neg q \vee r) \equiv \neg p \vee(\neg q \vee r)\) using truth table.
Answer:
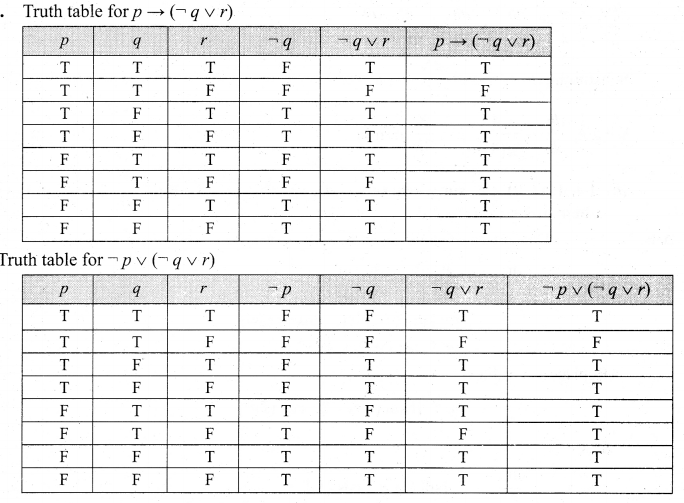
The entries in the column corresponding to \(p \rightarrow(\neg q \vee r) \text { and } \neg p \vee(\neg q \vee r)\) are identical.
Hence they are equivalent.
![]()
Question 46.
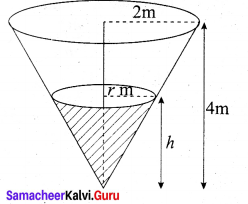
(a) A water tank has the shape of an inverted circular cone with base radius 2 metres and height 4 metres. If water is being pumped into the tank at a rate of 2m3/min, find the rate at which the water level is rising when the water is 3m deep.
Answer:
We first sketch the cone and label it as in diagram. Let V, r and h be respectively the volume of the water, the radius of the cone and the height at time t, where t is measured in minutes.
We are given that \(\frac{d \mathrm{V}}{d t}\) = 2m3/min and we are asked to find
\(\frac{d h}{d t}\) where h is 3m
The quantities V and h are related by the equation \(\mathrm{V}=\frac{1}{3} \pi r^{2} h\). But it is very useful to express V as function of h alone.
In order to eliminate r we use similar triangles in diagram to write \(\frac{r}{h}=\frac{2}{4} \Rightarrow r=\frac{h}{2}\) and the expression for V becomes \(\mathrm{V}=\frac{1}{3} \pi\left(\frac{h}{2}\right)^{2} h=\frac{\pi}{12} h^{3}\)
Now we can differentiate each side with respect to t and we have

(b) Let U (x, y) = ex sin y, where x = st2, y = s2t s, t e R. Find \(\frac{\partial \boldsymbol{U}}{\partial \boldsymbol{s}}, \frac{\partial \boldsymbol{U}}{\partial t}\) and evaluate them at s = t = 1.
Answer:

![]()
Question 47.
(a) The probability density function of X is given by f(x) = \(\begin{array}{c}
f(x)=\left\{\begin{array}{cc}
k e^{-\frac{x}{3}} & \text { for } x>0 \\
0 & \text { for } x \leq 0
\end{array}\right.
\end{array}\)
Find (i) the value of k
(ii) the distribution function
(iii) P(X < 3)
(iv) P(5 ≤ X) (v) P(X ≤ 4) .
Answer:

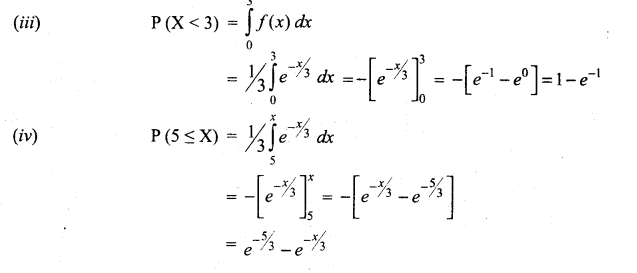

[OR]
(b) Solve [y(1 – xtanx) + x2cosx]dx – xdy = 0.
