Students can Download Tamil Nadu 11th Maths Model Question Paper 1 English Medium Pdf, Tamil Nadu 11th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
TN State Board 11th Maths Model Question Paper 1 English Medium
General Instructions:
- The question paper comprises of four parts.
- You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
- All questions of Part I, II, III and IV are to be attempted separately.
- Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer - Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
- Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
- Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.
Time: 2.30 Hours
Maximum Marks: 90
Part – I
Choose the correct answer. Answer all the questions. [20 × 1 = 20]
Question 1.
The number of students who take both the subjects Mathematics and Chemistry is 70. This represents 10% of the enrollment in Mathematics and 14% of the enrollment in Chemistry. The number of students take at least one of these two subjects, is
(a) 1120
(b)1130
(c) 1100
(d) insufficient data
Answer:
(b)1130
Question 2.
If 8 and 2 are the roots of x² + ax + c = 0 and 3, 3 are the roots of x² + dx + b = 0, then the roots of the equation x² + ax + b = 0 are
(a) 1, 2
(b) -1, 1
(c) 9, 1
(d) -1, 2
Answer:
(c) 9, 1
![]()
Question 3.
If tan 40° = λ then \(\frac{tan 140° – tan 130°}{1+tan 140° tan 130°}\) = ………….
(a) \(\frac{1-λ²}{λ}\)
(b) \(\frac{1+λ²}{λ}\)
(c) \(\frac{1+λ²}{2λ}\)
(d) \(\frac{1-λ²}{2λ}\)
Answer:
(d) \(\frac{1-λ²}{2λ}\)
Question 4.
The value of 2 sin A cos³ A – 2 cos A sin³ A is………..
(a) sin 4A
(b) cos 4A
(c) \(\frac{1}{2}\) sin 4A
(d) \(\frac{1}{2}\) cos 4A
Answer:
(c) \(\frac{1}{2}\) sin 4A
Question 5.
In a triangle ABC, sin²A + sin²B + sin²C = 2 then the triangle is ………. triangle.
(a) equilateral
(b) isosceles
(c) right
(d) scalene
Answer:
(c) right
Question 6.
The number of ways in which a host lady invite 8 people for a party of 8 out of 12 people of whom two do not want to attend the party together is ………….
(a) 2 × 11C7 + 10C8
(b) 11C7+ 10C8
(c) 12C8 – 10C6
(d) 10C6 + 2!
Answer:
(c) 12C8 – 10C6
Question 7.
If a is the arithmetic mean and g is the geometric mean of two numbers then…………
(a) a ≤ g
(b) a ≥ g
(c) a = g
(d) a > g
Answer:
(b) a ≥ g
Question 8.
The number of rectangles that a chessboard has…………
(a) 81
(b) 99
(c) 1296
(d) 6561
Answer:
(c) 1296
![]()
Question 9.
The intercepts of the perpendicular bisector of the line segment joining (1,2) and (3,4) with coordinate axes are………….
(a) 5, -5
(b) 5, 5
(c) 5, 3
(d) 5, -4
Answer:
(b) 5, 5
Question 10.
The coordinates of the four vertices of a quadrilateral are (-2, 4), (-1, 2), (1, 2) and (2, 4) taken in order.The equation of the line passing through the vertex (-1, 2) and dividing the quadrilateral in the equal areas is…………
(a) x + 1 = 0
(b) x + y= 1
(c) x + y + 3 = 0
(d) x – y + 3 = 0
Answer:
(c) x + y + 3 = 0
Question 11.
The vectors \(\vec{a}\) – \(\vec{b}\), \(\vec{b}\) – \(\vec{c}\), \(\vec{c}\) – \(\vec{a}\) are …………. vectors.
(a) parallel
(b) unit
(c) mutually perpendicular
(d) coplanar
Answer:
(d) coplanar
Question 12.
If |\(\vec{a}\) + \(\vec{b}\)| = 60, |\(\vec{a}\) – \(\vec{b}\)| = 40, |\(\vec{b}\)| = 46 then |\(\vec{a}\)| is ……………
(a) 42
(b) 12
(c) 22
(d) 32
Answer:
(c) 22
Question 13.
Given \(\vec{a}\) = 2\(\vec{i}\) + \(\vec{j}\) – 8\(\vec{k}\) and \(\vec{b}\) = \(\vec{i}\) + 3\(\vec{j}\) – 4\(\vec{k}\) then |\(\vec{a}\) + \(\vec{b}\)|= …………..
(a) 13
(b) \(\frac{13}{3}\)
(c) \(\frac{4}{13}\)
(d) \(\frac{3}{13}\)
Answer:
(a) 13
Question 14.
If \(\vec{r}\) = \(\frac{9\vec{a}+7\vec{b}}{16}\) then the point P whose position vector \(\vec{r}\) divides the line joining the points with position vectors \(\vec{a}\) and \(\vec{b}\) in the ratio……….
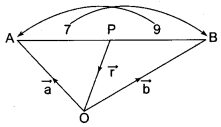
(a) 7 : 9 internally
(b) 9 : 7 internally
(c) 9 : 7 externally
(d) 7 : 9 externally
Answer:
(a) 7 : 9 internally
Question 15.
If f(x) = x + 2 then f’ (f(x)) at x = 4 is…………
(a) 8
(b) 1
(c) 4
(d) 5
Answer:
(b) 1
Question 16.
The derivative of (x + \(\frac{1}{x}\))² w.r.to. x is ……….
(a) 2x – \(\frac{2}{x³}\)
(b) 2x + \(\frac{2}{x³}\)
(c) 2(x + \(\frac{1}{x}\) )
(d) 0
Answer:
(a) 2x – \(\frac{2}{x³}\)
Question 17.
If y = \(\frac{1}{a-z}\) then \(\frac{dz}{dy}\) is………..
(a) (a – z)²
(b) – (z – a)²
(c) (z + a)²
(d) -(z + a)²
Answer:
(a) (a – z)²
![]()
Question 18.
∫sin7x cos5x dx = ……….

Answer:
(b) –\(\frac{1}{2}\) [\(\frac{cos 12x}{2}\) + \(\frac{cos 2x}{2}\)] + c
Question 19.
∫\(\frac{1}{e^x}\) dx = …………..
(a) log ex + c
(b) x + c
(c) \(\frac{1}{e^x}\) + c
(d) \(\frac{-1}{e^x}\) + c
Answer:
(d) \(\frac{-1}{e^x}\) + c
Question 20.
A letter is taken at random from the letters of the word ‘ASSISTANT’ and another letter is taken at random from the letters of the word ‘ STATISTICS ’. The probability that the selected letters are the same………..
(a) \(\frac{7}{45}\)
(b) \(\frac{17}{90}\)
(c) \(\frac{29}{90}\)
(d) \(\frac{19}{90}\)
Answer:
(d) \(\frac{19}{90}\)
PART- II
II. Answer any seven questions. Question No. 30 is compulsory. [7 × 2 = 14]
Question 21.
For a set A, A × A contains 16 elements and two of its elements are (1,3) and (0,2). Find the elements of A.
Answer:
A × A = 16 elements = 4 × 4
⇒ A has 4 elements
∴ A = {0, 1, 2, 3}
Question 22.
Find the area of the triangle whose sides are 13 cm, 14 cm and 15 cm.
Answer:
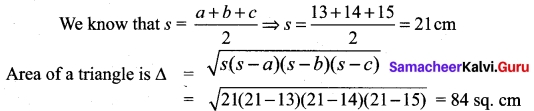
Question 23.
If \(\frac{1}{7!}\) + \(\frac{1}{9!}\) = \(\frac{x}{10!}\) find x.
Answer:
Here \(\frac{1}{7!}\) + \(\frac{1}{9!}\) = \(\frac{x}{10!}\)

Question 24.
Find \(\sqrt[3]{1001}\) approximately (two decimal places)
Answer:

Question 25.
The slope of one of the straight lines ax² + 2hxy + by² = 0 is three times the other, show that 3h² = 4 ab.
Answer:
Let the slopes be m and 3m.
Now m + 3m = 4m = –\(\frac{2h}{b}\)
⇒ m = –\(\frac{2h}{4b}\) = –\(\frac{h}{2b}\) …….. (1)
m × 3m = \(\frac{a}{b}\) ⇒ 3m² = \(\frac{a}{b}\) ⇒ m² = \(\frac{a}{3b}\) ………. (2)
Eliminating m from (1) and (2)
we get
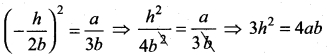
![]()
Question 26.
Simplify
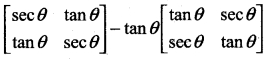
Answer:
If we denote the given expression by A, then using the scalar multiplication rule, we get

Question 27.
Find a point whose position vector has magnitude 5 and parallel to the vector 4\(\hat{i}\) – 3\(\hat{j}\) + 10\(\hat{k}\).
Answer:
Let \(\vec{a}\) be the vector 4\(\hat{i}\) – 3\(\hat{j}\) + 10\(\hat{k}\)
The unit vector \(\hat{a}\) along the direction of \(\hat{a}\) is \(\frac{\vec{a}}{|\vec{a}|}\) which is equal to \(\frac{4 \hat{i}-3 \hat{j}+10 \hat{k}}{5 \sqrt{5}}\). the vector whose magnitude is 5 and parallel to
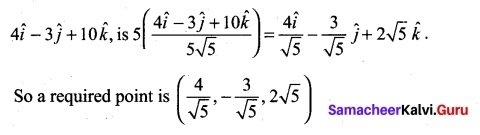
Question 28.
Evaluate \(\lim _{x \rightarrow-1}\left(x^{2}-3\right)^{10}\)
Answer:
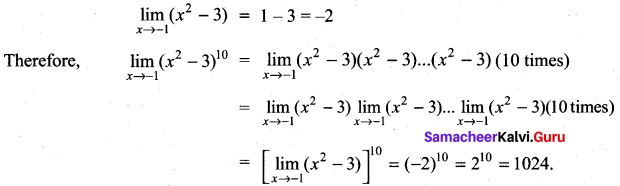
Question 29.
Evaluate \(\int \frac{e^{2 x}+e^{-2 x}+2}{e^{x}}\)
Answer:
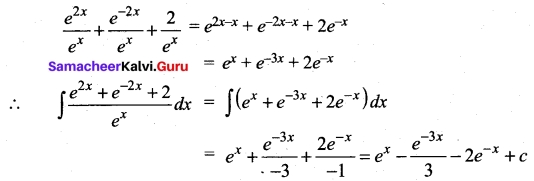
Question 30.
If A and B are mutually exclusive events P(A) = 3/8 and P(B) = 1/8 then find
(i) P(\(\bar{A}\) ∩ B)
(ii) p(\(\bar{A}\) ∪ \(\bar{B}\))
Answer:
(i) P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= 3/8 + 1/8 – 1/2
P(A ∩ B) = \(\frac{4-4}{8}\) = 0
P(\(\bar{A}\) ∩ B) = P(B) – P (A ∩ B) = 1/8 – 0 = 1/8
(ii) p(\(\bar{A}\) ∪ \(\bar{B}\)) = P[(A ∩B)’] = 1 – P(A ∩ B)
= 1 – 0 = 1
PART- III
III. Answer any seven questions. Question No. 40 is compulsory. [7 × 3 = 21]
Question 31.
Find the range of the function f(x) = \(\frac{1}{1-3cos x}\)
Answer:
Clearly, -1 ≤ cos x ≤ 1
⇒ 3 ≥ -3 cos x ≥ -3
⇒ -3 ≤ -3 cos x ≤ 3
⇒ 1 – 3 ≤ 1 – 3 cos x ≤ 1 + 3
Thus we get -2 ≤ 1 – 3 cos x and 1 – 3 cos x ≤ 4.
By taking reciprocals, we get \(\frac{1}{1-3 cos x}\) ≤ –\(\frac{1}{2}\) and \(\frac{1}{1-3 cos x}\) ≥ \(\frac{1}{4}\).
Hence the range of f is (-∞, –\(\frac{1}{2}\) ] ∪ [\(\frac{1}{4}\), ∞)
![]()
Question 32.
Solve for x, -x² + 3x – 2 ≥ 0
Answer:
-x² + 3x – 2 ≥ 0 ⇒ x² – 3x + 2 ≤ 0
(x – 1)(x – 2) ≤ 0
[(x – 1) (x – 2) = 0 ⇒ x = 1 or 2. Here α = 1 and β = 2. Note that α < β]
So for the inequality (x – 1) (x – 2) ≤ 2
x lies between 1 and 2
(i.e.) x ≥ 1 and x ≤ 2 or x ∈ [1, 2] or 1 ≤ x ≤ 2
Question 33.
Solve the following equation for which solutions lies in the interval 0° ≤ θ ≤ 360°. sin4x = sin²x
Answer:
sin²x – sin4x = 0
sin² x (1 – sin² x) = 0
sin²x (cos² x) = 0
[\(\frac{1}{2}\) (2 sinx cos x)]² = 0
⇒ (sin2 x)² = 0
⇒ sin 2x = 0 = 0, π, 2π, 3π, 4π
x = 0, \(\frac{π}{2}\), π, \(\frac{π}{2}\), 2π
Question 34.
Find n if n – 1 P3: nP4 = 1 : 9
Answer:
Here n – 1P3 : nP4 = 1 : 9

Question 35.
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5 kg includes the empty cylinders tare weight of 15.3 kg.). If it is used with constant rate then it lasts for 24 days. Then the new cylinder is replaced (i) Find the equation relating the quantity of gas in the cylinder to the days. (ii) Draw the graph for first 96 days.
Answer:
Since the usage is in constant rate and it is the slope m = \(\frac{14.2}{24}\)
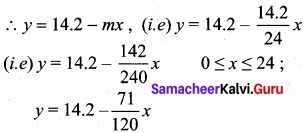
which is the equation relating the quantity.
y – f(x) is a periodic function with period 24. (i.e.) f(x) = f(x + 24)
Question 36.
If cos 2θ = 0, determine 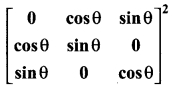
Answer:
Given cos 2θ = 0
⇒ 2θ = π/2 ⇒ θ = π/4

![]()
Question 37.
Show that the points (4, -3, 1), (2, -4, 5) and (1, -1, 0) form a right angled triangle.
Answer:
Trivially they form a triangle. It is enough to prove one angle is \(\frac{π}{2}\) . So find the sides of the triangle.
Let O be the point of reference and A, B, C be (4, -3, 1), (2, -4, 5) and (1, -1, 0) respectively.
\(\vec{OA}\) = 4\(\hat{i}\) -3\(\hat{j}\) + \(\hat{k}\), \(\vec{OB}\) = 2\(\hat{i}\) – 4\(\hat{j}\) + 5\(\hat{k}\), \(\vec{OC}\) = \(\hat{i}\) – \(\hat{j}\)
Now, \(\vec{AB}\) = \(\vec{OB}\) – \(\vec{OA}\) = -2\(\hat{i}\) – \(\hat{j}\) + 4\(\hat{k}\)
Similarly, \(\vec{BC}\) = –\(\hat{i}\) + 3\(\hat{j}\) – 5\(\hat{k}\); \(\vec{CA}\) = 3\(\hat{i}\) – 2\(\hat{j}\) + \(\hat{k}\)
Clearly \(\vec{AB}\) . \(\vec{CA}\) = 0
Thus one angle is \(\frac{π}{2}\). Hence they form a right angled triangle.
Question 38.
Compute
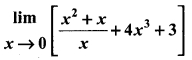
Answer:

= (0 + 1) + (0 + 3)
= 4
Question 39.
If for two events A and B, P(A) = \(\frac{3}{4}\), P(B) = \(\frac{2}{5}\) and A∪B conditional probability P(A/B).
Answer:
Given P(A) = \(\frac{3}{4}\), P(B) = \(\frac{2}{5}\) and P(A ∪ B) = l
Now P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
1 = \(\frac{3}{4}\) + \(\frac{2}{5}\) – P(A ∩ B)
P(A ∩ B) = \(\frac{3}{4}\) + \(\frac{2}{5}\) – 1 = \(\frac{15+8-20}{20}\)
P(A ∩ B) = 3/20
so P(A/B) = \(\frac{P(A ∪ B)}{P(B)}\) = \(\frac{3/20}{2/5}\) = \(\frac{3}{20}\) × \(\frac{5}{2}\) = \(\frac{3}{8}\)
Question 40.
Evaluate \(\int \frac{(x-1)^{2}}{x^{3}+x}\) dx
Answer:
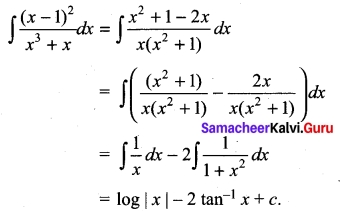
PART – IV
IV. Answer all the questions. [7 × 5 = 35]
Question 41 (a).
Find the range of the function
Answer:
The range of cos x is – 1 to 1
– 1 < cos x < 1
(x by 2) – 2 < 2 cos x < 2
adding -1 throughout
-2 – 1 < 2 cos x – 1 < 2 – 1
(i.e.,) -3 < 2 cos x -1 < 1
so 1 < \(\frac{1}{2cosx – 1}\) < \(\frac{-1}{3}\)
The range is outside \(\frac{-1}{3}\) and 1
i.e., range is (-∞, \(\frac{-1}{3}\)]∪[1, ∞)
[OR]
(b) In any triangle ABC prove that a² = (b + c)² sin² \(\frac{A}{2}\) + (b – c)² cos² \(\frac{A}{2}\) Answer:
RHS = (b + c)² sin² \(\frac{A}{2}\) + (b – c)² cos² \(\frac{A}{2}\)
= (b² + c² + 2bc) sin² \(\frac{A}{2}\) + (b² + c² – 2bc) cos² \(\frac{A}{2}\)
= (b² + c²) [sin² \(\frac{A}{2}\) + cos² \(\frac{A}{2}\)] + 2bc [sin² \(\frac{A}{2}\) – cos² \(\frac{A}{2}\)]
= b² + c² – 2bc cos A = a² = LHS
![]()
Question 42 (a).
Find all values of x for which \(\frac{x³(x-1)}{x-2}\) > 0
Answer:
\(\frac{x³(x-1)}{x-2}\) > 0
Now we have to find the signs of
x³, x – 1 and x – 2 as follows
x³ = 0 ⇒ x = 0; x – 1 = 0 ⇒ x = 1; x – 2 = 0 ⇒ x = 2.
Plotting the points in a number line and finding intervals
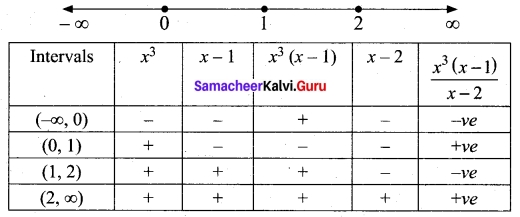
So the solution set = (0, 1) ∪ (2, ∞)
[OR]
(b) resolve \(\frac{x}{(x²+1)(x-1)(x+2)}\) Into partial fractions.
Answer:

Equating numerator on both sides
x = A (x + 2) (x² + 1) + B (x – 1) (x² + 1) + (Cx + D) (x – 1) (x + 2)
This equations is true for any value of x to find A, B, C and D.
put x = 1
1 = A (3) (2) + B (0) + (0)
6A = 1 ⇒ A= 1/6
put x = -2
-2 = + 0 + B (-3) (5) + 0
⇒ -15B = -2 ⇒ B = 2/15
put x = 0
⇒ 2A – B – 2D = 0
(i.e.,) \(\frac{2}{6}\) – \(\frac{2}{15}\) – 2D = 0

![]()
Question 43 (a).
7 relatives of a man comprises 4 ladies and 3 gentlemen, his wife has also 7 relatives; 3 of them are ladies and 4 gentlemen. In how many ways can they invite a dinner party of 3 ladies and 3 gentlemen so that there are 3 of mens relative and 3 of the wifes relatives?
Answer:
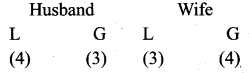
We need 3 ladies and 3 gentlemen for the party which consist of 3 Husbands relative and 3 wifes relative.
This can be done as follows

4C0 = 4C4 = 1; 3C0 = 3C3 = 1
4C1 = 4C3 = 4; 3C1 = 3C2 = 3
4C2 = \(\frac{4×3}{2×1}\) = 6
(4) (1) (1) (4) + (6) (3) (3) (6) + (4) (3) (3) (4) + (1) (1) (1) (1)
= 16 + 324 + 144 + 1 = 485 ways.
[OR]
(b) Show that the points (1, 3), (2, 1) and (\(\frac{1}{2}\), 4) are collinear, by using
(i) Concept of slope
(ii) Using a straight line and
(iii) Any other method.
Answer:
Let the given points be A (1, 3), B (2, 1), and C(\(\frac{1}{2}\), 4)
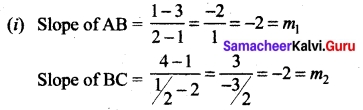
Slope of AB = Slope of BC ⇒ AB parallel to BC but B is a common point.
⇒ The points A, B, C are collinear.
(ii) Equation of the line passing through A and B is \(\frac{y-1}{3-1}\) = \(\frac{x-2}{1-2}\) ⇒ \(\frac{y-1}{2}\) = \(\frac{x-2}{-1}\)
1 – y = 2x – 4
2x +y = 5 ……….(1)
Substituting C\(\frac{1}{2}\), 4 in (1),
We get LHS = 2(\(\frac{1}{2}\)) + 4 = 1 + 4 = 5 = RHS
C is a point on AB
⇒ The points A, B, C lie on a line.
⇒ The points A, B, C are collinear.
(iii) Area of ΔABC = \(\frac{1}{2}\)(x1) (y2 y3) + x2 (y3 – y1) + x3 (y1 – y2)
= \(\frac{1}{2}\) {1(1, -4) + 2(4 – 3) +\(\frac{1}{2}\)(3 – 1)} = \(\frac{1}{2}\)(-3 + 2 + 1) = 0
⇒ The points A, B, C are collinear.
![]()
Question 44 (a).
Prove by vector Method’s that the Medians of a triangle are concurrent.
Answer:
Theorem: The medians of a triangle are concurrent.
Proof: Let ABC be a triangle and let D, E, F be the mid points of its sides BC, CA and AB respectively. We have to prove that the medians AD, BE, CF are concurrent.
Let O be the origin and \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) be the position vectors of A, B, and C respectively.
The position vectors of D, E and F are respectively.
\(\frac{\vec{b}}{\vec{c}}\), \(\frac{\vec{c}}{\vec{a}}\), \(\frac{\vec{a}}{\vec{b}}\)
Let G1, be the point on AD dividing it internally in the ratio 2 : 1.
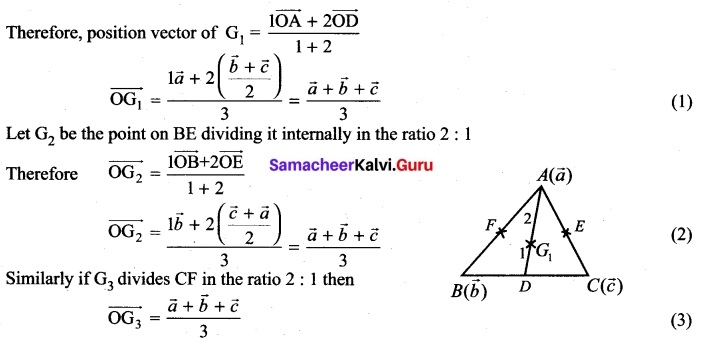
From (1), (2) and (3) we find that the position vectors of the three points G1, G2, G3 are one and the same. Hence they are not different points. Let the common point be G.
Therefore the three medians are concurrent and the point of concurrence is G.
[OR]
(b) If y = Ae6x + Be-x prove that \(\frac{d²y}{dx²}\) – 5\(\frac{dy}{dx}\) – 6y = 0
Answer:

Question 45 (a).
If a and b are distinct integers, prove that a – b is a factor of an – bn, whenever n is a positive integer. [Hint: write an = (a-b + b)n and expand]
Answer:
a = a – b + b
So, an = [a – b + b]n =[(a – b) + b]n
= nC0 (a – b)n + nC1 (a -b)n-1b1 + nC2 (a – b)n-2b² + ……… + nCn-1(a – b) bn-1
+ nCn(bn)
⇒ an – bn = (a – b)n + nC1 (a – b)n-1b + nC2 (a – b)n-2b² + ……. + nCn-1 (a – b) bn-1
= (a – b) [(a – b)n-1 + nC1(a – b)n-2b + nC2 (a – b)n-3b² + ……… + nCn-1, bn-1]
= (a – b) [an integer]
⇒ an – 6n is divisible by (a – b)
[OR]
(b) Verify the property A (B + C) = AB + AC when the matrices A, B and C are given by
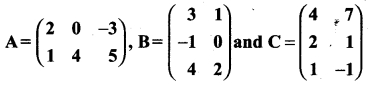
Answer:

![]()
Question 46 (a).
Evaluate \(\lim _{x \rightarrow \infty} \sqrt{x^{2}+x+1}-\sqrt{x^{2}+1}\)
Answer:
Here the expression assumes the form ∞ to – ∞ as x → ∞. SO, we first reduce it to the rational form \(\frac{f(x)}{g(x)}\)

[OR]
(b) Evaluate \(\lim _{x \rightarrow \infty} x\left[3^{\frac{1}{x}}+1-\cos \left(\frac{1}{x}\right)-e^{1 / x}\right]\)
Answer:
Let y = \(\frac{1}{x}\) as x → ∞, y → 0

Question 47 (a).
Evaluate \(\int \tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right)\) dx.
Answer:

[OR]
(b) Suppose the chances of hitting a target by a person X is 3 times in 4 shots, by Y is 4 times in 5 shots, and by Z is 2 times in 3 shots. They fire simultaneously exactly one time. What is the probability that the target is damaged by exactly 2 hits?
Answer:
Given P(X) = 3/4, P(X’) = 1 – 3/4 = 1/4
P(Y) = 4/5, P(Y’) = 1 – 4/5 = 1/5
P(Z) = \(\frac{2}{3}\) P(Z’) = 1 – \(\frac{2}{3}\) = \(\frac{1}{3}\)

![]()