Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 3 Perimeter and Area Ex 3.2

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 3 Perimeter and Area Ex 3.2

Miscellaneous Practice Problems

Question 1.
A piece of wire is 36 cm long. What will be the length of each side if we form
i) a square
ii) an equilateral triangle.
Solution:
Given the length of the wire = 36 cm
i) When a square is formed out of it
The perimeter of the square = 36 cm
4 × side = 36
side = \(\frac{36}{4}\) = 9 cm
Side of the square

ii) When an equilateral triangle is formed out of it, its perimeter = 36 cm
i.e., side + side + side = 36 cm .
3 × side = 36 cm
side = \(\frac{36}{3}\) = 12 cm
One side of an equilateral triangle = 12 cm

Question 2.
From one vertex of an equilateral triangle with side 40 cm, an equilateral triangle with 6 cm side is removed. What is the perimeter of the remaining portion?
Solution:

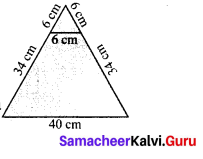
If an equilateral triangle of side 6 cm is removed the perimeter = (40 + 34 + 6 +34) cm = 114 cm
Perimeter of the remaining portion = 114 cm

Question 3.
Rahim and peter go for a morning walk, Rahim walks around a square path of side 50 m and Peter walks around a rectangular path with length 40 m and breadth 30 m. If both of them walk 2 rounds each, who covers more distance and by how much?
Solution:
Perimeter of the square = (4 × sides) units
side of the square = 50 m
∴ Perimeter = 4 × 50 m = 200 m
Rahim walked twice around the park.
∴ Total distance walked by Rahim = 2 × 200m
Total distance covered by Rahim = 400m
Perimeter of a rectangle = 2 (length + breadth) unit
Length = 40 m
Breadth = 30 m
∴ perimeter = 2 × (40 + 30) m = (2 × 70) m = 140 m
Peter walked around twice
∴ Distance covered by Peter = 2 × 140 m = 280 m
∴ Distance covered by Peter = 280 m
400 m > 280 m
Difference = 480 – 280 = 120 m
∴ Rahim covers 120m more than Peter

Question 4.
The length of a rectangular park is 14 m more than its breadth. If the perimeter of the park is 200 m, what is its length? Find the area of the park?
Solution:
Given length of rectangular park is 14m more than its breadth.
Let the breadth be b m .
∴ Length of the park will be l = b + 14 m
Given perimeter = 200 m
2 × (l + b) = 200 m
2 × (b + 14 + b) = 200 m [∵ l = b + 14]
2 × (2b + 14) = 200 m
2b + 14 = \(\frac{200}{2}\) m
2b + 14 = 100 m
2b = 100 – 14 m
2b = 86 m
b = \(\frac{86}{2}\) m
b 43 m
Length Length of the park = 57 m
Area of a rectangle = (length × breadth) unit²
= (57 × 43) m² = 2,451 m²
Area of the park = 2,451 m²

Question 5.
Your garden is in the shape of a square of side 5 m. Each side is to be fenced with 2 rows of wire. Find how much amount is needed to fence the garden at Rs 10 per meter.
Solution:Perimeter of a square = (4 × side) units
side = 5 m
∴ Perimeter = (4 × 5) m = 20 m
Each side is fenced with 2 rows of wire
∴ Distance to be fenced = 2 × 20 m = 40 m
Cost of fencing per metre = ₹ 10
∴ Cost of fencing 40 m = 40 × 10 = ₹ 400
Cost of fencing the garden = ₹ 400

Challenge Problems

Question 6.
A closed shape has 20 equal sides and one of its sides is 3 cm. Find its perimeter.
Solution:
Number of equal sides in the shape = 20
One of its side = 3 cm
Perimeter = length of one side × Number of equal sides
∴ Perimeter = (3 × 20) cm = 60 cm
∴ Perimeter = 60 cm

Question 7.
A rectangle has length 40 cm and breadth 20 cm. How many squares with side 10 cm can be formed from it.
Solution:
l = 40 cm, b = 20 cm
Area of the rectangle = l × b sq units
= 40 × 20 cm²
= 800 cm²
a = 10 cm
Area of the square = a × a sq. units
= 10 × 10 cm²
= 100 m²
No of squares formed = \(\frac{800}{100}\) cm²
= 8

Question 8.
The length of a rectangle is three times its breadth. If its perimeter is 64 cm, find the sides of the rectangle.
Solution:
Length l = 3b
breadth = b
perimeter = 64 cm
2 (l + b) = 64 cm
2(3b + b) = 64
2 (4b) = 64
8b = 64
b = \(\frac{64}{8}\)
breadth b = 8 cm
length l = 3b
l = 3 × 8
= 24 cm

Question 9.
How many different rectangles can be made with a 48 cm long string? Find the possible pairs of length and breadth of the rectangles.
Solution:
12 rectangles
(1, 23), (2, 22), (3, 21), (4, 20), (5, 19), (6, 18), (7, 17), (8, 16), (9, 15), (10, 14), (11, 13), (12, 12)

Question 10.
Draw a square B whose side is twice of the square A. Calculate the perimeters of the squares A and B.
Solution:

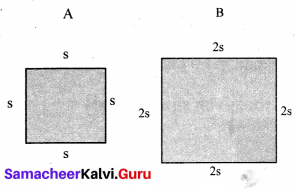
The perimeter of square B = 4 × 4 m = 16 m
The perimeter of square A = 4 × 2 m = 8 m
The perimeter of square B is twice that of square A.

Question 11.
What will be the area of a new square formed if the side of a square is made one – fourth?
Solution:
Let the side of square is s units then area = (s × s) units²
If the side of the new square is made one fourth then side = \(\left(\frac{1 \times s}{4}\right)\) units
Then area = \(\left(\frac{1 \times s}{4} \times \frac{1 \times s}{4}\right)\) units² = \(\frac{s \times s}{16}=\frac{1}{16}\) (s × s) units²
Area of the new square is reduced to \(\frac{1}{16}\) times to that of original area.

Question 12.
Two plots have the same perimeter. One is a square of side 10 m and another is a rectangle of breadth 8 m. Which plot has the greater area and by how much?
Solution:

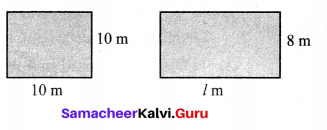
Given perimeter of square = perimeter of rectangle
4 × side = 2 (length + breadth)
(4 × 10) m = 2(l + 8)m
\(\frac{4 \times 10}{2}\) = l + 8
20 = l + 8
l = 20 – 8
l = 12 m
∴ length of the rectangle = 12 m
Area of the square plot – side × side = 10 × 10 m² = 100 m²
Area of the rectangular plot = length × breadth = (12 × 8) m² = 96 m²
100 m² > 96 m²
∴ Square plot has greater area by 4m²

Question 13.
Look at the picture of the house given and find the total area of the shaded portion.

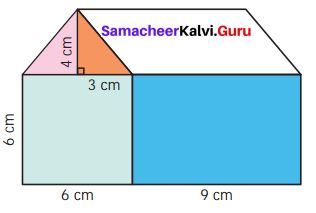
Solution:
Area of a square = a × a sq.units
= 6 x 6 cm²
= 36 cm²
Area of a rectangle = l × b sq units
= 9 x 6 cm²
= 54 cm²
Area of a triangle = \(\frac{1}{2}\) × b × h sq.units
= \(\frac{1}{2}\) × 4² × 6 cm²
= 12 cm²
Total area of the shaded portion
= (36 + 54 + 12) cm²
= 102 cm²

Question 14.
Find the approximate area of the flower in the given square grid.

Solution:
Approximate area = Number of full squares + Number of more than half squares + \(\frac{1}{2}\) × Number of half squares.
= 10 + 5 + (\(\frac{1}{2}\) × 1) Sq units. = 10 + 5 + \(\frac{1}{2}\) sq. units
= 15 \(\frac{1}{2}\) sq. units = 15.5 sq. units.