Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.4

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.4

Question 1.
Find the next three terms of the following sequence.
(i) 8, 24, 72, …….
(ii) 5, 1, -3, …….
(iii) \(\frac { 1 }{ 4 } \),\(\frac { 2 }{ 9 } \),\(\frac { 3 }{ 16 } \)………..
Solution:
(i) 8, 24, 72…
In an arithmetic sequence a = 8,
d = t₁ – t₁ = t₃ – t₂
= 24 – 8       72 – 24
= 16 ≠ 48
So, it is not an arithmetic sequence. In a geometric sequence,
r = \(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}\)
⇒ \(\frac{24}{8}=\frac{72}{24}\)
⇒ 3 = 3
∴ It is a geometric sequence
∴ The n^th term of a G.P is t_n = ar^n-1
∴ t₄ = 8 × 3^4-1
= 8 × 3³
= 8 × 27
= 216

t₅ = 8 × 3^5-1
= 8 × 3⁴
= 8 × 81
= 648

t₆ = 8 × 3^6-1
= 8 × 3⁵
= 8 × 243
= 1944
The next 3 terms are 8, 24, 72, 216, 648, 1944.

(ii) 5, 1, -3, …
d = t₂ – t₁ = t₃ – t₂
⇒ 1 – 5 = -3-1
-4 = -4 ∴ It is an A.P.
t_n = a+(n – 1)d
t₄ = 5 + 3 × – 4
= 5 – 12
= -7
15 = a + 4d
= 5 + 4 × -4
= 5 – 16
= -11
t₆ = a + 5d
= 5 + 5 × – 4
= 5 – 20
= – 15
∴ The next three terms are 5, 1, -3, -7, -11, -15.

(iii) \(\frac { 1 }{ 4 } \),\(\frac { 2 }{ 9 } \),\(\frac { 3 }{ 16 } \),………..
Here a_n = Numerators are natural numbers and denominators are squares of the next numbers
\(\frac { 1 }{ 4 } \),\(\frac { 2 }{ 9 } \),\(\frac { 3 }{ 16 } \),\(\frac { 4 }{ 25 } \),\(\frac { 5 }{ 36 } \),\(\frac { 6 }{ 49 } \)………….

Question 2.
Find the first four terms of the sequences whose n^th terms are given by

(i) a_n = n³ -2
Answer:
a_n = n³ – 2
a₁ = 1³ – 2 = 1 – 2 = -1
a₂ = 2³ – 2 = 8 – 2 = 6
a₃ = 3³ – 2 = 27 – 2 = 25
a₄ = 4³ – 2 = 64 – 2 = 62
The four terms are -1, 6, 25 and 62

(ii) a_n = (-1)ⁿ⁺¹ n(n + 1)
Answer:
a_n = (-1)ⁿ⁺¹ n(n + 1)
a₁ = (-1)² (1) (2) = 1 × 1 × 2 = 2
a₂ = (-1)³ (2) (3) = -1 × 2 × 3 = -6
a₃ = (-1)⁴ (3) (4) = 1 × 3 × 4 = 12
a₄ = (-1)⁵ (4) (5) = -1 × 4 × 5 = -20
The four terms are 2, -6, 12 and -20

(iii) a_n = 2n² – 6
Answer:
a_n = 2 n² – 6
a₁ = 2(1)² – 6 = 2 – 6 = -4
a₂ = 2(2)² – 6 = 8 – 6 = 2
a₃ = 2(3)² – 6 = 18 – 6 = 12
a₄ = 2(4)² – 6 = 32 – 6 = 26
The four terms are -4, 2, 12, 26

Question 3.
Find the n^th term of the following sequences
(i) 2, 5, 10, 17, ……….
(ii) 0, \(\frac { 1 }{ 2 } \), \(\frac { 2 }{ 3 } \),…..
(iii) 3, 8, 13, 18, ………
Solution:
(i) 2, 5, 10, 17
= 1² + 1, 2² + 1, 3² + 1, 4² + 1 ……….
∴ n^th term is n²+1
(ii) 0, \(\frac { 1 }{ 2 } \),\(\frac { 2 }{ 3 } \),………….
= \(\frac { 1-1 }{ 1 } \),\(\frac { 2-1 }{ 2 } \),\(\frac { 3-1 }{ 3 } \)…..
⇒ \(\frac { n-1 }{ n } \)
∴ nth term is \(\frac { n-1 }{ n } \)
(iii) 3, 8, 13, 18
a = 3
d = 5
t_n = a + (n – 1)d
= 3 + (n – 1)5
= 3 + 5n – 5
= 5n – 2
∴ n^th term is 5n – 2

Question 4.
Find the indicated terms of the sequences whose n^th terms are given by
(i) a_n = \(\frac { 5n }{ n+2 } \) ; a₆ and a₁₃
(ii) a_n = -(n² – 4); a₄ and a₁₁
Solution:

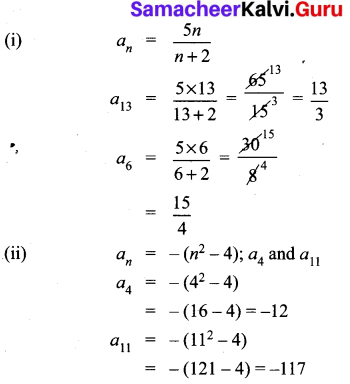
Question 5.
Find a₈ and a₁₅ whose n^th term is

Solution:

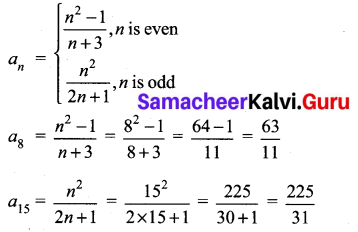
Question 6.
If a₁ = 1, a₂ = 1 and a_n = 2a_n-1 + a_n-2 n > 3, n ∈ N. Then find the first six terms of the sequence.
Answer:
a₁ = a₂ = 1
a_n = 2a_n-1 + a_n-2
a₃ = 2a_3-1 + a_3-2 = 2a₂ + a₁
= 2(1) + 1 = 3
a₄ = 2a_4-1 + a_4-2
= 2a₃ + a₂
= 2(3) + 1 = 6 + 1 = 7
a₅ = 2 a_5-1 + a_5-2
= 2a₄ + a₃
= 2(7) + 3 = 17
a₆ = 2a_6-1 + a_6-2
= 2a₅ + a₄
= 2(17) + 7
= 34 + 7 = 41
The sequence is 1, 1, 3, 7, 17,41, …