Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.4

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 1 Set Language Ex 1.4

Question 1.
If P= {1, 2, 5, 7, 9}, Q = {2, 3, 5, 9, 11}, R = {3, 4, 5, 7, 9} and S = {2, 3, 4, 5, 8}, then find
(i) (P ∪ Q) ∪ R
(ii) (P ∩ Q) ∩ S
(iii) (Q ∩ S) ∩ R
Solution:
(i) (P ∪ Q) ∪ R
(P ∪ Q) = {1, 2, 5, 7, 9} ∪ {2, 3, 5, 9, 11} = {1, 2, 3, 5, 7, 9, 11}
(P ∪ Q) ∪ R = {1, 2, 3, 5, 7, 9, 11} ∪ {3, 4, 5, 7, 9} = {1, 2, 3, 4, 5, 7, 9, 11}

(ii)(P ∩ Q) ∩ S
(P ∩ Q) = {1, 2, 5, 7, 9} ∩ {2, 3, 5, 9, 11} = {2, 5, 9}
(P ∩ Q) ∩ S = {2, 5, 9} ∩ {2, 3, 4, 5, 8} = {2, 5}

(iii) (Q ∩ S) ∩ R
(Q ∩ S) = {2, 3, 5, 9, 11} ∩ {2, 3, 4, 5, 8} = {2, 3, 5}
(Q ∩ S) ∩ R = {2, 3, 5} ∩ {3, 4, 5, 7, 9} = {3, 5}

Question 2.
Test for the commutative property of union and intersection of the sets
P = {x : x is a real number between 2 and 7} and
Q = {x : x is an irrational number between 2 and 7}
Solution:
Commutative Property of union of sets
(A ∪ B)’ = (B ∪ A)
Here P = {3, 4, 5, 6}, Q = {\(\sqrt{3}, \sqrt{5}, \sqrt{6}\)}
P ∪ Q = {3, 4, 5, 6} ∪ {\(\sqrt{3}, \sqrt{5}, \sqrt{6}\)} = {3, 4, 5, 6, \(\sqrt{3}, \sqrt{5}, \sqrt{6}\)} …………. (1)
Q ∪ P = {\(\sqrt{3}, \sqrt{5}, \sqrt{6}\)} ∪ {3, 4, 5, 6}= {\(\sqrt{3}, \sqrt{5}, \sqrt{6}\), 3, 4, 5, 6} ………… (2)
(1) = (2)
∴ P ∪ Q = Q ∪ P
∴ It is verified that union of sets is commutative.
Commutative Property of intersection of sets (P ∩ Q) = (Q ∩ P)
P ∩ Q = {3, 4, 5, 6} ∩ {\(\sqrt{3}, \sqrt{5}, \sqrt{6}\)} = { } ………. (1)
Q ∩ P = {\(\sqrt{3}, \sqrt{5}, \sqrt{6}\)} ∩ {3, 4, 5, 6} = { } …………. (2)
From (1) and (2)
P ∩ Q = Q ∩ P
∴ It is verified that intersection of sets is commutative.

Question 3.
If A = {p, q, r, s}, B = {m, n, q, s, t} and C = {m, n, p, q, s}, then verify the associative property of union of sets.
Solution:
Associative Property of union of sets
A ∪ (B ∪ C) = (A ∪ B) ∪ C)
B ∪ C = {m, n, q, s, t} ∪ {m, n,p, q, s}= {m, n, p, q, s, t}
A ∪ (B ∪ C) = {p, q, r, s} ∪ {m, n, p, q, s, t} = {m, n, p, q, r, s, t} ………..… (1)
(A ∪ B) = {p, q, r, s} ∪ {m, n, q, s, t} = {p, q, r, s, m, n, t}
(A ∪ B) ∪ C = {p, q, r, s, m, n, t} ∪ {m, n, p, q, s} = {p, q, r, s, m, n, t} …………… (2)
From (1) & (2)
It is verified that A ∪ (B ∪ C) = (A ∪ B) ∪ C

Question 4.
Verify the associative property of intersection of sets for A = {-11, \(\sqrt{2}, \sqrt{5}\) ,7}, B = {\(\sqrt{3}, \sqrt{5}\), 6, 13} and C = {\(\sqrt{2}, \sqrt{3}, \sqrt{5}\), 9}.
Solution:
Associative Property of intersection of sets A ∩ (B ∩ C) = (A ∩ B) ∩ C)

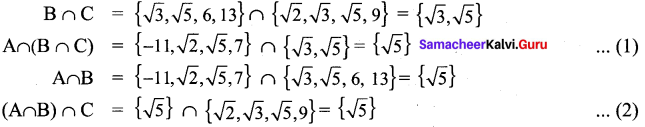
From (1) and (2), it is verified that A ∩ (B ∩ C) = (A ∩ B) ∩ C

Question 5.
If A = {x : x = 2ⁿ, n ∈ W and n < 4}, B = {x: x = 2 n, n ∈ N and n ≤ 4} and C = {0, 1, 2, 5, 6}, then verify the associative property of intersection of sets.
Solution:
A = {x : x = 2ⁿ, n ∈ W, n < 4}
⇒ x = 2°= 1
x = 2¹ = 2
x = 2² = 4
x = 2³ = 8
∴ A = {1, 2, 4, 8}

B = {x : x = 2n, n ∈ N and n ≤ 4}
⇒ x = 2 × 1 = 2
x = 2 × 2 = 4
x = 2 × 3 = 6
x = 2 × 4 = 8
∴ B = {2, 4, 6, 8}
C = {0, 1, 2, 5, 6}
Associative property of intersection of sets
A ∩ (B ∩ C) = (A ∩ B) ∩ C
B ∩ C = {2, 6}
A ∩ (B ∩ C) = {1, 2, 4, 8} ∩ {2, 6} = {2} ………..… (1)
A ∩ B = {1, 2, 4, 8} ∩ {2, 4, 6, 8} = {2, 4, 8}
(A ∩ B) ∩ C = {2, 4, 8} ∩ {0, 1, 2, 5, 6} = {2} …………….. (2)
From (1) and (2), It is verified that A ∩ (B ∩ C) = (A ∩ B) ∩ C