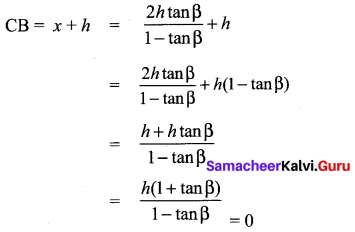Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Ex 6.5

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Ex 6.5

Multiple choice questions.
Question 1.
The value of \(\sin ^{2} \theta+\frac{1}{1+\tan ^{2} \theta}\) is equal to
(1) tan²θ
(2) 1
(3) cot²θ
(4) 0
Solution:
(2) 1
Hint:

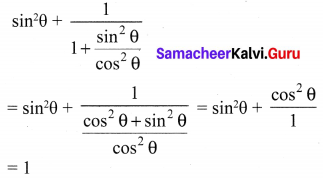
Question 2.
tan θ cosec²θ – tan θ is equal to
(1) sec θ
(2) cot²θ
(3) sin θ
(4) cot θ
Solution:
(4) cot θ
Hint:

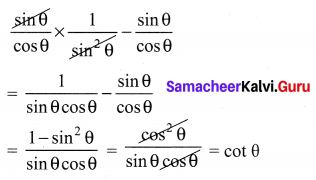
Question 3.
If (sin α + cosec α)² + (cos α + sec α)² = k + tan² α + cot² α, then the value of k is equal to
(1) 9
(2) 7
(3) 5
(4) 3
Solution:
(2) 7
Hint:
(sin α + cosec α)² + (cos α + sec α)² = k + tan² α + cot² α
sin² α + cosec² α + 2 sin α cosec α + cos² α + sec² α + 2 cos α sec α = k + tan² α + cot² α
sin² α + cos² α + cosec² α + sec² α + 2 sin α × \(\frac{1}{\sin \alpha}\) + 2 cos α × \(\frac{1}{\cos \alpha}\) = k + tan² α + cot² α
1 + 1 + cot² α + 1 + tan² α + 2 + 2 = k + tan² α + cot² α
7 + cot² α + tan² α = k + tan² α + cot² α
∴ k = 7

Question 4.
If sin θ + cos θ = a and sec θ + cosec θ = b, then the value of b(a² – 1) is equal to
(1) 2a
(2) 3a
(3) 0
(4) 2ab
Solution:
(1) 2a
a = sin θ + cos θ
b = sec θ + cosec θ

Question 5.
If 3x = sec θ and \(\frac{5}{x}\) = tan θ, then \(x^{2}-\frac{1}{x^{2}}\) is
(1) 25
(2) \(\frac{1}{25}\)
(3) 5
(4) 1
Solution:

Question 6.
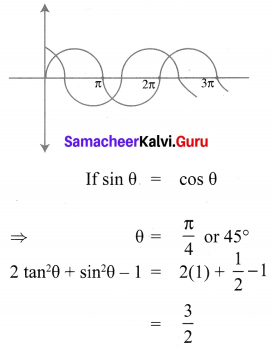
If sin θ = cos θ , then 2 tan²θ + sin²θ – 1 is equal to
(1) \(\frac{-3}{2}\)
(2) \(\frac{3}{2}\)
(3) \(\frac{2}{3}\)
(4) \(\frac{-2}{3}\)
Solution:
(2) \(\frac{3}{2}\)
Hint:

Question 7.
If x = a tan θ and y = b sec θ then

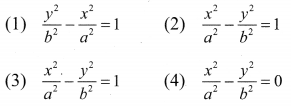
Solution:
(1) \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}=1\)
Hint:

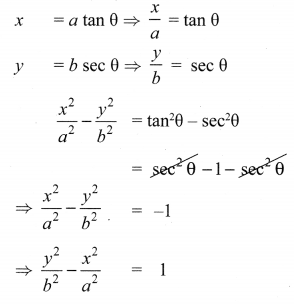
Question 8.
(1 + tan θ + sec θ) (1 + cot θ – cosec θ) is equal to
(1) 0
(2) 1
(3) 2
(4) -1
Solution:
(3) 2
Hint:

Question 9.
a cot θ + b cosec θ = p and b cot θ + a cosec θ = q then p² – q² is equal to ………….
(1) a² – b²
(2) b² – a²
(3) a² + b²
(4) b – a
Answer:
(2) b² – a²
Hint:
p² – q² = (p + q) (p – q)
= (a cot θ + b cosec θ + b cot θ + a cosec θ) (a cot θ + b cosec θ – b cot θ – a cosec θ)
= [cot θ (a + b) + cosec θ (a + b)] [cot θ (a – b) + cosec θ (b – a)]
= (a + b) [cot θ + cosec θ] (a – b) [cosec θ (a – b)]
= (a + b) [cot θ + cosec θ] (a – b) [cot θ – cosec θ]
= (a + b) (a – b) (cot² θ – cosec² θ)
= (a² – b²) (-1) = – (a² – b²)
p² – q² = b² – a^2.

Question 10.
If the ratio of the height of a tower and the length of its shadow is \(\sqrt{3}\) : 1, then the angle of elevation of the sun has measure.
(1) 45°
(2) 30°
(3) 90°
(4) 60°
Solution:
(4) 60°
Hint:

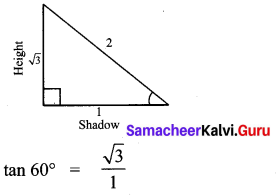
Question 11.
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the tower is 60°. The height of the tower (in metres) is equal to

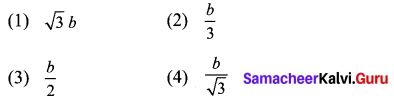
Solution:
(2) \(\frac{b}{3}\)
Hint:

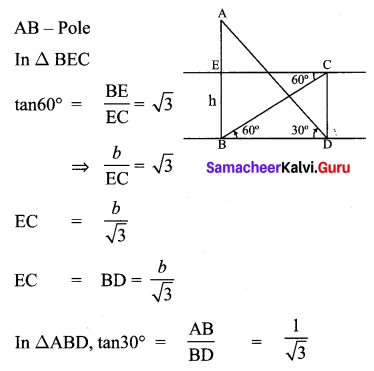
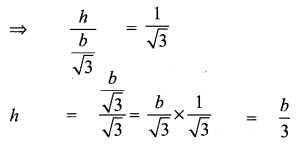
Question 12.
A tower is 60 m height. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
(1) 41.92 m
(2) 43.92 m
(3) 43 m
(4) 45.6 m°
Solution:
(2) 43.92 m
Hint:

Question 13.
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
(1) 20, 10\(\sqrt{3}\)
(2) 30, 5\(\sqrt{3}\)
(3) 20, 10
(4) 30, 10\(\sqrt{3}\)
Solution:
(4) 30, 10\(\sqrt{3}\)
Hint:


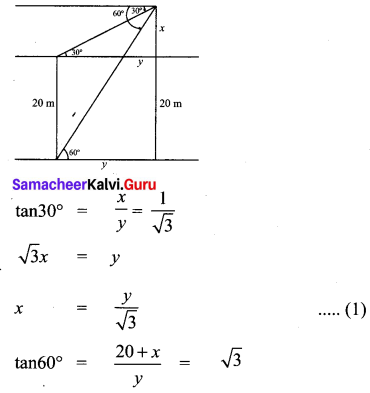
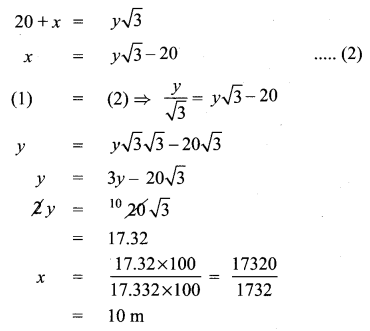
∴ Height of tower = 20 + 10 = 30 m
distance = 17.32 m = 10\(\sqrt{3}\)

Question 14.
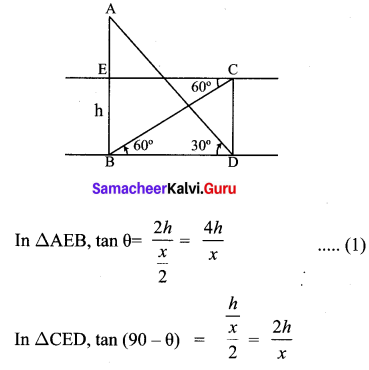
Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is

Solution:
(2) \(\frac{x}{2 \sqrt{2}}\)
Hint:

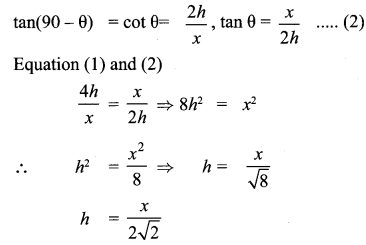
Question 15.
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is

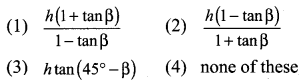
Solution:
(1) \(\frac{h(1+\tan \beta)}{1-\tan \beta}\)
Hint: