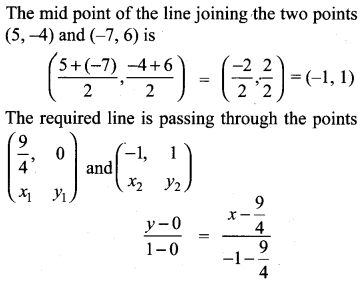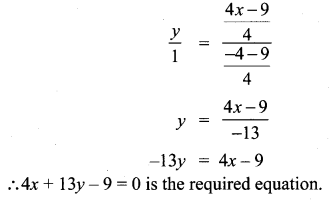Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.4

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.4

Question 1.
Find the slope of the following straight lines
(i) 5y – 3 = 0
(ii) \(7 x-\frac{3}{17}\) = 0
Solution:

Question 2.
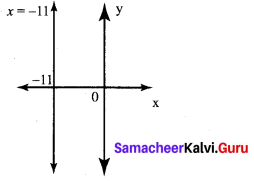
Find the slope of the line which is
(i) parallel to y = 0.7x -11
(ii) perpendicular to the line x = -11
Solution:
(i) y = 0.7x – 11
line parallel to y = 0.7x – 11 is y = 0.7x + C
If the lines are parallel, slopes are equal
∴ The slope of the required line is 0.7.
(ii) m = tan θ = tan 90°= ∞ undefined.

Question 3.
Check whether the given lines are parallel or perpendicular

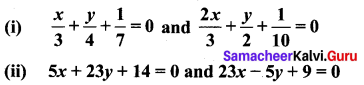
Solution:
(i) \(\frac{x}{3}+\frac{y}{4}+\frac{1}{7}\) = 0

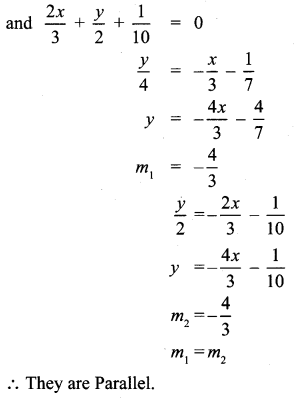
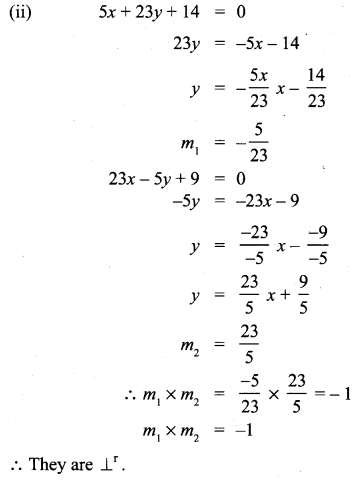
Question 4.
If the straight lines 12y = -(p + 3)x + 12, 12x – 7y = 16 are perpendicular then find ‘p’.
Solution:

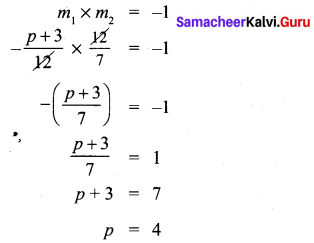
Question 5.
Find the equation of a straight line passing through the point P (-5, 2) and parallel to the line joining the points Q(3, -2) and R(-5, 4).
Solution:

Question 6.
Find the equation of a line passing through ; (6, -2) and perpendicular to the line joining the points (6, 7) and (2, -3).
Solution:
Slope of line joining (6, 7) and (2,-3) is

Question 7.
A(-3, 0) B(10, – 2) and C(12, 3) are the vertices of ∆ABC . Find the equation of the altitude through A and B.
Solution:
A(-3, 0), B(10, -2), C(12, 3)
Since AD ⊥ BC



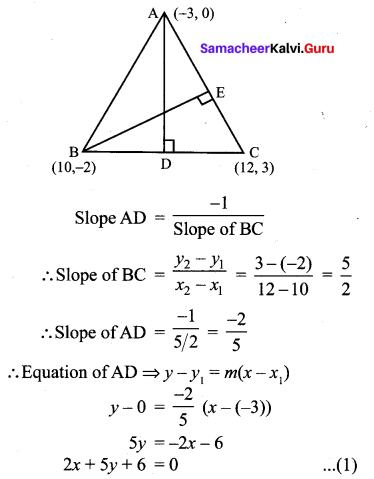
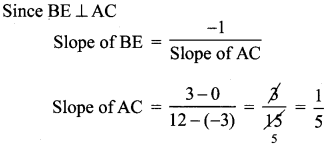
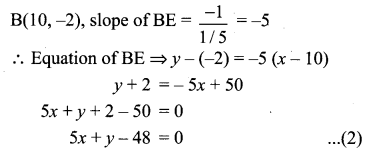
(1), (2) are the required equations of the altitudes through A and B.

Question 8.
Find the equation of the perpendicular bisector of the line joining the points A(-4, 2) and B(6, -4).
Solution:
Mid Point AB is

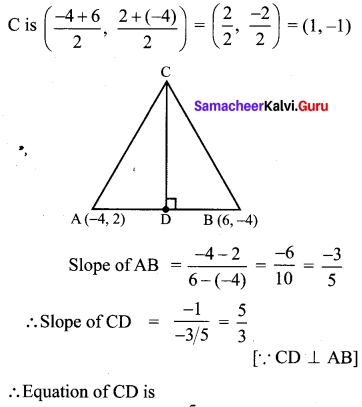
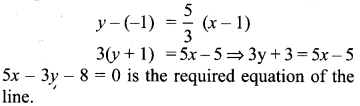
Question 9.
Find the equation of a straight line through the intersection of lines 7x + 3y = 10, 5x – 4y = 1
and parallel to the line 13x + 5y + 12 = O
Solution:

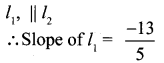
l₁ passes through the intersecting point.

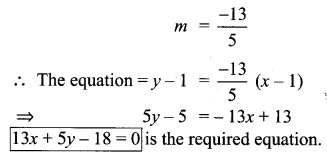
Question 10.
Find the equation of a straight line through the intersection of lines 5x – 6y = 2, 3x + 2y = 10 and perpendicular to the line 4x – 7y + 13 = 0
Solution:

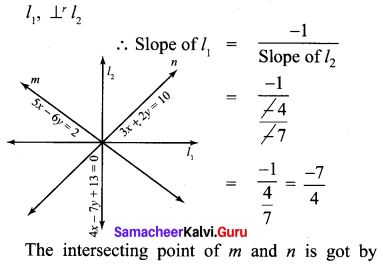
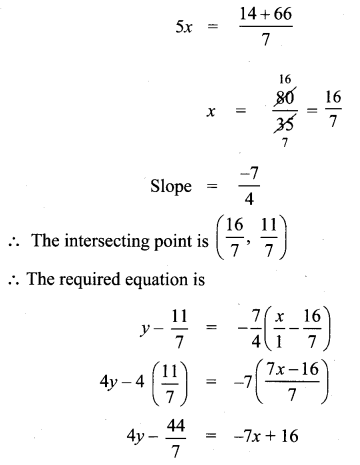
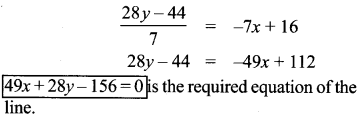
Question 11.
Find the equation of a straight line joining the point of intersection of 3x + y + 2 = 0 and x – 2y – 4 = 0 to the point of intersection of 7x – 3y = -12 and 2y = x + 3
Solution:

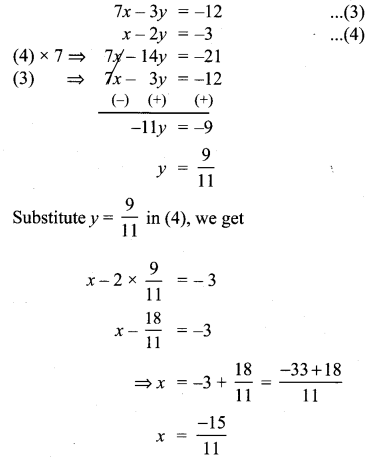
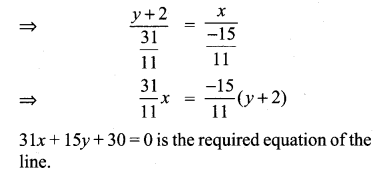
Question 12.
Find the equation of a straight line through the point of intersection of the lines 8x + 3+ = 18, 4x + 5+ = 9 and bisecting the line segment joining the points (5, -4) and (-7, 6).
Solution:
The intersecting point of the lines