Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Additional Questions

Students can Download Maths Chapter 3 Algebra Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 3 Algebra Additional Questions

Additional Questions And Answers

Exercise 3.1

Very Short Answers [2 Marks]

Question 1.
Find the product of the following.
(i) (x, y)
(ii) (10x, 5y)
(iii) (2x², 5y²)
Solution:
(i) x × y = xy
(ii) 10x × 5y = (10 × 5) x × xy
= 50 xy
(iii) 2x² x 5y² = (2 x 5) x (x² + y²)
= 10x²y²

Short Answers [3 Marks]

Question 1.
Find the product of the following.
(i) 3ab² c³ by 5a³b²c
(ii) 4x²yz by \(\frac{3}{2}\) x²yz²
Solution:
(i) (3ab³c³) × (5a³b²c)
= (3 × 5)(a × a³ × b² × b² × c² × c)
= 15a¹⁺³.b²⁺².c³⁺¹ = 15a⁴b⁴c⁴

(ii) 4x²yz by \(\frac{3}{2}\) x²yz²
= (4 × \(\frac{3}{2}\)) × (x² × x² × y × y × z × z²)
= -6x²⁺² y¹⁺¹ x¹⁺² = -6x⁴y²z³

Long Answers [5 Marks]

Question 1.
Simplify (3x – 2) (x – 1) (3x + 5).
Solution:
(3x – 2) (x – 1) (3x + 5)
= {(3x – 2) (x – 1)} × (3x + 5) [∴Multiplication in associative]
= {3x (x – 1) – 2 x – 1)} × (3x + 5)
= (3x² – 3x – 2x + 2) × (3x + 5)
= (3x² – 5x + 2) (3x + 5)
= 3x² × (3x + 5) – 5x (3x + 5) + 2 (3x + 5)
= (9x³ + 15x²) + (-15x² – 25x) + (6x + 10)
= 9x³ + 15x² – 15x² – 25x + 6x + 10
= 9x³ – 19x + 10

Question 2.
Simplify (5 – x) (3 – 2x) (4 – 3x).
Solution:
(5 – x) (3 – 2x) (4 – 3x)
= {(5 – x)(3 – 2x)} × (4 – 3x) [∴ Multiplication in association]
= {5 (3 – 2x) -x (3 – 2x)} × (4 – 3x)
= (15 – 10x – 3x + 2x²) × (4 – 3x)
= (2x² – 13x + 15) (4 – 3x)
= 2x² × (4 – 3x) – 13x (4 – 3x) + 15 (4 – 3x)
= 8x³ – 6³ – 52x + 39x² + 60 – 45x
= -6x³ + 47x² – 97x + 60

Exercise 3.2

Very Short Answers [2 Marks]

Question 1.
Divide.
(i) 12x³y³ by 3x²y
(ii) -15a² bc³ by 3ab
(iii) 25x³y² by – 15x²y
Solution:

Short Answers [3 Marks]

Question 1.
Divide
(i) 15m²n³ by 5m²n²
(ii) 24a³b³ by -8ab
(iii) -21 abc² by 7 abc
Solution:

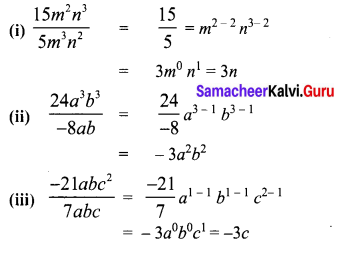
Question 2.
Divide
(i) 16m³y² by 4m²y
(ii) 32m² n³p² by 4mnp
Solution:

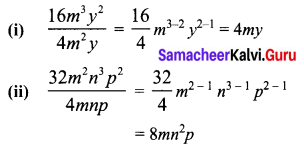
Long Answers [5 Marks]

Question 1.
Divide.
(i) 9m⁵ + 12m⁴ – 6m² by 3m²
(ii) 24x³y + 20x²y² – 4xy by 2xy
Solution:

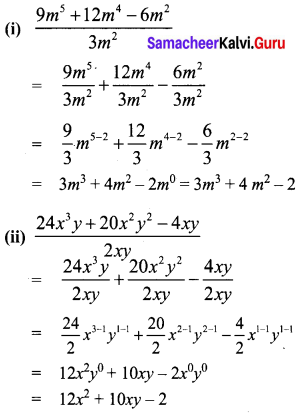
Exercise 3.3

Question 1.
Evaluate:
(i) (2x + 3y)²
(ii) (2x – 3y)²
Solution:
(i) (2x + 3y)²
= (2x)² + 2 × (2x) × (3y) + (3y)²
[using (a + b)² = a² + 2ab + b²]
= 4x² + 12xy + 9y²

(ii) (2x – 3y)²
= (2x)² – 2(2x) (3y) + (3y)²
[∵ using (a – b)² = a² – 2ab + b²]
= 4x² – 12xy + 9y²

Short Answers [3 Marks]

Question 1.
Evaluate the following
(i) (2x – 3) (2x + 5)
(ii) (y – 7) (y + 3)
(iii) 107 × 103
Solution:
(i) (2x – 3) (2x + 5)
= (2x)² + (-3 + 5) (2x) + (-3) (5)
[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= 2²x² + 2 × 2x + (-15)
= 4x² + 4x – 15

(ii) (y – 7) (y + 3)
= y² + (-7 + 3)y + (-7) (3)
[∵ (x + a)(x + b) = x² + (a + b)x + ab]
= y² – 4y + (-21) = y² – 4y – 21

(iii) 107 × 103
= (100 + 7) × (100+ 3)
= 100² + (7 + 3) × 100 +(7 × 3)
= 10000 + 10 × 100 + 21 = 10000 + 1000 + 21 = 11021

Long Answers [5 Marks]

Question 1.
If x + y = 12 and xy = 14 find x² + y².
Solution:
(x + y)² = x² + y² + 2xy
12² = x² + y² + 2 × 14
144 = x² + y² + 28
x² + y² = 144 – 28
x² + y² = 116

Question 2.
If 3x + 2y = 12 and xy = 6 find the value of 9x² + 4y².
Solution:
(3x + 2y)² = (3x)² + (2y)² + 2 (3x) (2y)
= 9x² + 4y² + 12xy
12² = 9x² + 4y² + 12 × 6
144 = 9x² + 4y² + 72
144 – 72 = 9x² + 4y²
∴ 9x² + 4y² = 72

Exercise 3.4

Question 1.
Factorize:
(i) 7(2x + 5) + 3 (2x + 5)
(ii) 12x³y⁴ + 16x²y⁵ – 4x⁵y²
Solution:
(i) 7(2x + 5) + 3 (2x + 5)
= (2x + 5) (7 + 3)
(ii) 12x³y⁴ + 16x²y⁵ – 4x⁵y²
= 4x²y² (3xy² + 4y³ – x³)

Short Answers [3 Marks]

1. Factorize
(i) 81a² – 121b²
(ii) x² + 8x + 16
Solution:
(i) 81a² – 121b²
= (9a)² – (11b)²
[∵ using a² – b² = (a + b)²]
= (9a + 11b) (9a – 11b)

(ii) x² + 8x + 16 = x² + 2 × x × 4 + 4²
[∵ using a² + 2ab + b² = (a + b)²]
= (x + 4)² = (x + 4)(x + 4)

Long Answers [5 Marks]

Question 1.
Factorize
(i) x² + 2xy + y² – a² + 2ab – b²
(ii) 9 – a⁶ + 2a³ – b⁶
Solution:
(i) x² + 2xy + y² – a² + 2ab – b².
= (x² + 2xy + y²) – (a² – 2ab + b²)
= (x + y)² – (a – b)²
= {(x + y) + (a – b)} {(x + y) – (a – b)}
= (x + y + a – b) (x + y – a + b)

(ii) a – a⁶ + 2a³b³ – b⁶
= 9 – (a⁶ – 2a³b³ + b⁶)
= 3² -{(a³)² – 2 × a³ × b³ + (b³)²}
= 3² – (a³ – 6³)²
= {3 + (a³ – b³)} {3 – (a³ – b³)}
= (3 + a³ – b³) (3 – a³ + b³)
= (a³ – b³ + 1){-a³ + b³ + 3)

Question 2.
Factorize
(i) 100 (x + y )² – 81 (a + b)²
(ii)(x + 1)² – (x – 2)²
Solution:
(i) 100 (x + y)² – 81 (a + b)²
= {10 (x + y)}² – {(a (a + b)}²
= {10 (x + y) + 9 (a + b)}
{10 (x + y) – 9(a + b)}
= (10x + 10y + 9a – 9b)}
(10x + 10y – 9a – 9b)

(ii) (x – 1)² – (x – 2)²
= {(x – 1 +(x – 2)}
{(x – 1) – (x – 2)}
= (2x – 3) – (x – 1 – x + 2)
= (2x – 3) × 1 = 2x – 3