Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.2

You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3.2

Question 1.
Find the value of the polynomial f(y) = 6y – 3y² + 3 at (i) y = 1 (ii) y = -1 (iii) y = 0
Solution:
(i) At y = 1,
f(1) = 6(1) – 3(1)² + 3 = 6 – 3 + 3 = 6
(ii) At y = -1,
f(-1) = 6(-1) – 3(-1)² + 3 = -6 – 3 + 3 = -6
(iii) At y = 0,
f(0) = 6(0) – 3(0)² + 3 = 0 – 0 + 3 = 3

Question 2.
If f(x) = x² – \(2 \sqrt{2} x\) + 1, find p (\(2 \sqrt{2}\))
Solution:
p(\(2 \sqrt{2}\)) = (\(2 \sqrt{2}\))² – \(2 \sqrt{2}\)(\(2 \sqrt{2}\)) + 1
= 4 × 2 – 4 × 2 + 1
= 8 – 8 + 1 = 1

Question 3.
Find the zeros of the polynomial in each of the following :
(i) p(x) = x – 3
(ii) p(x) = 2x + 5
(iii) q(y) = 2y – 3,
(iv) f(z) = 8z
(v) p(x) = ax where a ≠ 0,
(vi) h(x) = ax + b, a ≠ 0, a, b ∈ R
Solution:
(i) x = 3.
p( 3) = 3 – 3 = 0
∴ The zero of the polynomial is x = 3.

(iv) f(z) = 8z,
If 8z = 0
z = \(\frac{0}{8}\) = 0
f(0) = 8(0) = 0
∴ z = 0 is the zero of the given polynomial.

Question 4.
Find the roots of the polynomial equations.
(i) 5x – 6 = 0
(ii) x + 3 = 0
(iii) 10x + 9 = 0
(iv) 9x – 4 = 0
Solution:
(i) 5x – 6 = 0
5x = 6
∴ x = \(\frac{6}{5}\)

(ii) x + 3 = 0
∴ x = -3

(iii) 10x + 9 = 0
10x = -9
∴ x = \(\frac{-9}{10}\)

(iv) 9x – 4 = 0
9x = 4
∴ x = \(\frac{4}{9}\)

Question 5.
Verify whether the following are zeros of the polynomial indicated against them, or not.
(i) p(x) = 2x – 1, x = \(\frac{1}{2}\)
(ii) p(x) = x³ – 1, x = 1,
(iii) p(x) = ax + b, x = \(\frac{-b}{a}\)
(iv) p(x) = (x + 3) (x – 4), x = 4, x = -3
Solution:
(i) p(x) = 2x – 1, x = \(\frac{1}{2}\)
p(\(\frac{1}{2}\)) = 2(\(\frac{1}{2}\)) – 1 = 1 – 1 = 0
∴ x = \(\frac{1}{2}\) is the zero of the given polynomial.

(ii) p(x) = x³ – 1, x = 1
p(1) = 1³ – 1 = 1 – 1 = 0
∴ x = 1 is the zero of the given polynomial

(iii) p(x) = ax + b, x = \(\frac{-b}{a}\)
p(\(\frac{-b}{a}\)) = a(\(\frac{-b}{a}\)) + b
= -b + b = 0
∴ x = \(\frac{-b}{a}\) is the zero of the given polynomial.

(iv) p(x) = (x + 3) (x – 4), x = 4, x = -3
p(-3) = (-3 + 3) (-3 – 4) = 0(-7) = 0
p(4) = (4 + 3) (4 – 4) = 7(0) = 0
∴ x = -3, x = 4 are the zeros of the given polynomial.

Question 6.
Find the number of zeros of the following polynomial represented by their graphs.

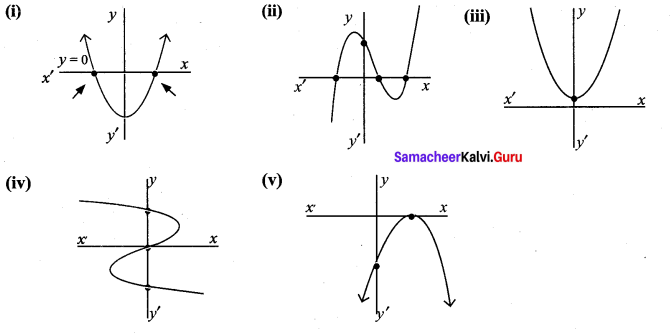
Solution:
(i) The curve cuts the x-axis at two points. ∴ The equation has 2 zeros.
(ii) Since the curve cuts the x-axis at 3 different points. The number of zeros of the given curve is three.
(iii) Since the curve doesn’t cut the x axis. The number of zeros of the given curve is zero.
(iv) The curve cut the x-axis at one point. ∴ The equation has one zero.
(v) The curve cut the x axis at one point. ∴ The equation has one zero.