Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.3

Students can Download Maths Chapter 2 Measurements Ex 2.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.3

Question 1.
Fill in the blanks:
(i) The three dimensions of a cuboid are _____.
(ii) The meeting point of more than two edges- is called as ______.
(iii) A cube has _____ faces.
(iv) The cross section of a solid cylinder is ______.
(v) If a net of a 3-D shape has six plane squares, then it is called ______.
Solution:
(i) length, breadth and height
(ii) vertex
(iii) six
(iv) circle
(v) cube

Question 2.
Match the following:

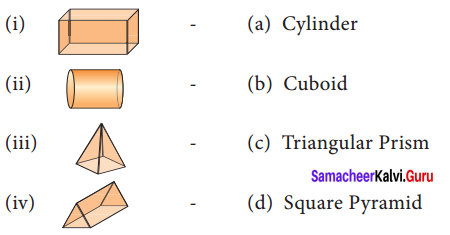
Solution:
(i) b
(ii) a
(iii) d
(iv) c

Question 3.
Which 3-D shapes do the following nets represent? Draw them.

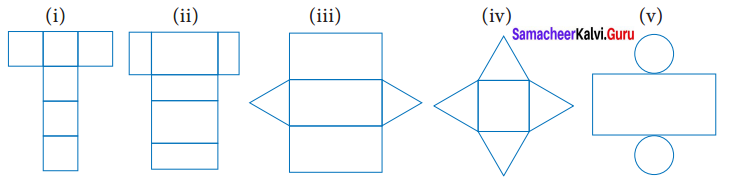
Solution:
(i) The net represents cube, because it has 6 squares

(ii) The net represents cuboid

(iii) The net represents Triangular prism

(iv) The net represents square pyramid

(v) The net represents cylinder

Question 4.
For each solid, three views are given. Identify for each solid, the corresponding top, front and side (T, F & S) views.

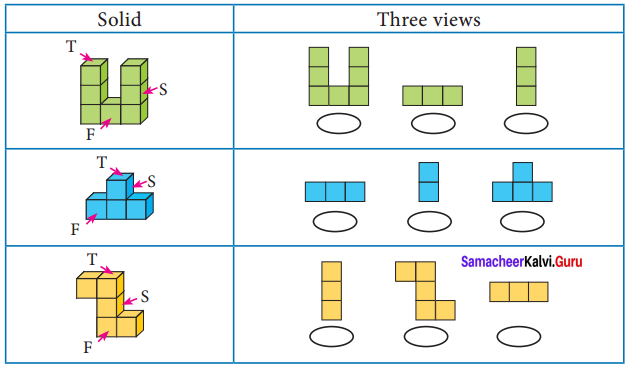
Solution:

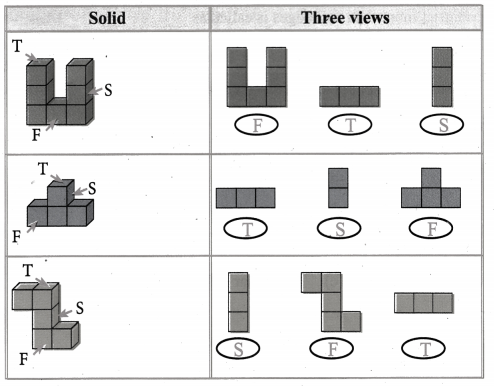
Question 5.
Verify Euler’s formula for the table given below

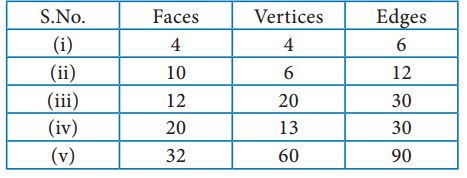
Solution:
Euler’s formula is given by F + V – E
(i) F = 4 ; V = 4; E = 6
F + V – E = 4 + 4 – 6 = 8 – 6
F + V – E = 2
∴ Euler’s formula is satisfied.

(ii) F = 10; V = 6; E = 12
F + V – E = 10 + 6 – 12
= 16 – 12 = 4 ≠ 2
∴ Euler’s formula is not satisfied.

(iii) F = 12 ; V = 20 ; E = 30
F + V – E = 12 + 20 – 30
= 32 – 30 = 2
∴ Euler’s formula is satisfied.

(iv) F = 20 ; V = 13 ; E = 30
F + V – E = 20 + 13 – 30
= 33 – 30 = 3 ≠ 2
∴ Euler’s formula is not satisfied.

(v) F = 32 ; V = 60 ; E = 90
F + V – E = 32 + 60 – 90
= 92 – 90 = 2
∴ Euler’s formula is satisfied.

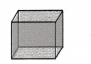
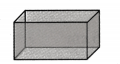
Question 6.
Find the area of the given nets.

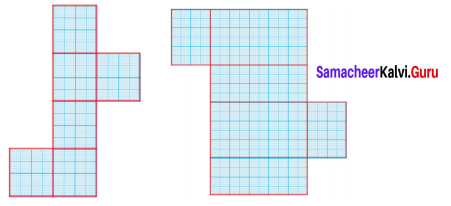
Solution:
(i) Area = Area of 6 squares of side 4 cm
= 6 × a² sq. units
= 6 × 4 × 4 cm²
= 96 cm²
(ii) Area = Area of 2 rectangles of
l = 10, b = 6 + Area of 2 rectangles of l = 6, b = 4 + Area of 2 rectangles of l= 10,b = 4
= (10 × 6) + (6 × 4)+ (10 × 4) cm²
= 60 + 24 + 40 cm²
= 124 cm²

Question 7.
Can a polyhedron have 12 faces, 22 edges and 17 vertices?
Solution:
By Euler’s formula F + V- E = 2 fora polyhedron.
Here F = 12, V = 17, E = 22
F + V – E = 12 + 17 – 22
= 29 – 22
= 7 ≠ 2
∴ The polyhedron cannot have 12 faces 22 edges and 17 vertices.