Students can Download Maths Chapter 5 Geometry Ex 5.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 5 Geometry Ex 5.4
Question 1.
Construct the following angles using protractor and draw a bisector to each of the angle using ruler and compass.
(a) 60°
(b) 100°
(c) 90°
(d) 48°
(e) 110°.
Solution:
(a) 60°
Construction:
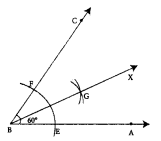
Step 1: Drawn the given angle ∠ABC with the measure 60° using protractor.
Step 2: With B as centre and convenient radius, drawn an arc to cut BA and BC. Marked the points of intersection as E on BA and F on BC.
Step 3: With the same radius and E as centre drawn an arc in the interior of ∠ABC and another arc of same measure with centre at F to cut the previous arc.
Step 4: Marked the point of intersection as G. Drawn a ray BX through G. BG is the required bisector of the given ∠ABC
![]()
(b) 100°
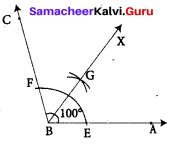
Construction :
Step 1: Drawn the given angle ∠ABC with the measure 100° c using protractor.
Step 2: With B as centre and convenient radius, drawn an arc to cut BA and BC. Marked the points of intersection as E on BA and F on BC.
Step 3: With the same radius and E as centre drawn an arc in the interior of ∠ABC and another arc of the same measure with centre at F to cut the previous arc.
Step 4: Marked the point of intersection at G. Drawn a ray BX through G.
BG is the required bisector of angle ∠ABC
∠ABG = ∠GBC = 50°
![]()
(c) 90°
Construction :
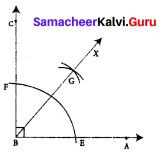
Step 1: Drawn the given angle ∠ABC with the measure 90° using protractor.
Step 2: With B as center and convenient radius, drawn an arc to cut BA and BC. Marked the points of intersection as E on BA and F on BC.
Step 3: With the same radius and E as center drawn an arc in the interior of ∠ABC and another arc of same measure with center at F to cut the previous arc.
Step 4: Mark the point of interaction as G. Drawn a ray BX through G. BG is the required bisector of the given angle ∠ABC
∠ABG = ∠GBC = 45°
(d) 48°
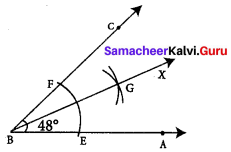
Construction :
Step 1: Drawn the given angle ∠ABC with the measure 48° using protractor.
Step 2: With B as center and convenient radius, drawn an arc to cut BA and to cut BA and BC. Marked the points of intersection as E on BA and F on BC.
Step 3: With the same radius and E as center drawn an arc in the interior of ∠ABC and another arc of the same measure with center at F to cut the previous arc.
Step 4: Marked the point of intersection as G. Drawn a ray BX through G. BG is the required bisector of the given angle ∠ABC
Now ∠ABC = ∠GBC = 24°
![]()
(e) 110°
Construction:
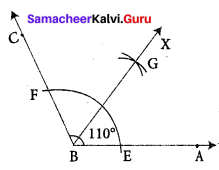
Step 1: Drawn the given angle ∠ABC with the measure 110° using protractor.
Step 2: With B as center and convenient radius, drawn an arc to cut BA and BC. Marked points of intersection as E on BA and F BC.
Step 3: With the same radius and E as center, drawn an arc in the interior of ∠ABC and another arc of same measure with center at F to cut the previous arc.
Step 4: Mark the point of intersection as G. Drawn a ray BX through G. BG is the
required bisector of the given angle ∠ABC
∠ABG = ∠GBC = 55°