You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 1 Numbers Additional Questions
Answer the following questions.
![]()
Question 1.
How many thousands are there in 1 lakhs?
Solution:
\(\frac{1,00,0000}{1000}\) = 100 Thousands
Question 2.
The difference between successor and predecessor of any number is 2. Is it true? Justify your answer.
Solution:
It is true that the difference between successor and predecessor of any number is 2.
Because the difference between any number and its predecessor is 1.
Also the difference between the number and its successor is 1.
The total difference is 2.
Question 3.
The expanded form of the number 6,00,001 is given as 6 × 100000 + 1 × 1. Can you write like this Comment.
Solution:
Yes. We can write the expansion of the number 600001 as 6 × 100000 + 1 × 1.
Because 6 × 100000 + 1 × 1 = 600000 + 1 = 600001
Question 4.
Write the greatest five digit number using the digits 2, 3, 4, 0 and 7.
Solution:
Greatest five digit number = 74320
Question 5.
Can you write the least five digit number using the digits 2,3,4,0 and 7 as 02347. Why? What will be the correct number?
Solution:
No, we cannot write the least five digit number using the digits 2, 3, 4, 0 and 7 as 02347. If it is 02347, the left most zero has no value. It becomes 4 digit number 2347.
The correct number will be 20347.
![]()
Question 6.
Write the relation between Largest two digit number and Smallest three digit number.
Solution:
Largest two digit number + 1 = Smallest three digit number.
99 + 1 = 100
Question 7.
Name the property being illustrated in each of the cases.
- (30 + 20) + 10 = 30 + (20 + 10)
- 10 × 35 = (10 × 30) + (10 × 5)
Solution:
- Associativity
- Distribution of multiplication over addition.
Question 8.
10 crore = ____
Solution:
100 million
Question 9.
The heights of five boys in class VI are 135, 141, 129, 132, 145 (in centimetres) in height. Arrange their heights as how they stand in the assembly?
Solution:
129 cm < 132 cm < 135 cm < 141 cm < 145 cm
Question 10.
The number lock has the password number with 3 digits. The number is the least even number and less than 200. Middle digit has no value separately. Find the password. The digits are used only once.
Solution:
102
Question 11.
Arrange in ascending order. 123456, 123546, 123623, 123511
Solution:
123456 < 123511 < 123546 < 123623 Question 12. Arrange in descending order. 8461, 7535, 2943, 6214 Solution: 8461 > 7535 > 6214 > 2943
![]()
Question 13.
Find the numbers between 572634 and 562634 which is approximated to ten thousand place.
Solution:
562634 < 570000 < 572634
Question 14.
Evaluate the following:
(a) 44 ÷ 2 + (7 + 80 ÷ 10) – 14 + 23
(b) 17 × 6 – 4 – 2 + 20 – (22 + 18)
(c) 16 × 144 ÷ 16 ÷ 9 + 16 + 15 – 20
(d) 12 × 36 ÷ 12 ÷ 3 + 5 + 6 – 2
(e) 15 – [17 + 30 ÷ 6 – (6 + 6) + 7]
Solution:
(a) 44 ÷ 2 + (7 + 80 ÷ 10) – 14 + 23 (Given)
= 44 ÷ 2 + (7 + 8) – 14 + 23 (To complete the bracket ÷ done first)
= 44 ÷ 2 + 15 – 14 + 23 (Bracket completed second)
= 22 + 15 – 14 + 23 (÷ completed third)
= 37 – 37 (+ completed fourth)
= 0 (- completed last)
∴ 44 ÷ 2 + (7 + 80 ÷ 10) – 14+ 23 = 0.
(b) 17 × 6 – 4 – 2 + 20 – (22 + 18) (Given)
= 17 × 6 – 4 – 2 + 20 – 40 (Bracket completed first)
= 102 – 4 – 2 + 20 – 40 (× completed second)
= 102 – 4 – 22 – 40 (+ completed third)
= 98 – 22 – 40 (÷ completed one by one)
= 76 – 40
= 36
∴ 17 × 6 – 4 – 2+ 20 – (22 + 18) = 36
(c) 16 × 144 ÷ 16 ÷ 9 + 16 + 15 – 20 (Given)
= 16 × 9 ÷ 9+16 + 15 – 20 (÷ completed first)
= 16 × 1 + 16 + 15 – 20 (÷ completed second)
= 16 + 16 + 15 – 20 (× completed third)
= 32 + 15 – 20 (+ completed fourth)
= 47 – 20 (+ completed fifth)
= 27 (- completed last)
∴ 16 × 144 ÷ 16 ÷ 9 + 16 + 15 – 20 = 27
(d) 12 × 36 ÷ 12 ÷ 3 + 5 + 6 – 2 (Given)
= 12 × 3 ÷ 3 + 5 + 6 – 2 (÷ completed first)
= 12 × 1 + 5 + 6 – 2 (÷ completed second)
= 12 + 5 + 6 – 2 (× completed third)
= 17 + 6 – 2 (+ completed forth)
= 23 – 2 (+ completed fifth)
= 21 (- completed last)
∴ 12 × 36 ÷ 12 ÷ 3 + 5 + 6 – 2 = 21
(e) 15 – [17 + 30 ÷ 6 – (6 + 6) + 7] (Given)
= 15 – [17 + 30 ÷ 6 – 12 + 7] (Inner bracket completed first)
= 15 – [17 + 5 – 12 + 7] (÷ completed second)
= 15 – [22 – 19] (+ completed third)
= 15 – 3 (bracket completed forth)
= 12 (- completed last)
∴ 15 – [17 + 30 ÷ 6 – (6 + 6) + 7] = 12.
![]()
Question 15.
An export company produced 235219 shirts, 158342 trousers and 11704 jackets in a year. What is the total production of all the three items in that year?
Solution:
Number of shirts produced = 235219
Number of trousers produced = 158342
Number of jackets produced = 11704
Total production of all items = 405265
Total production of all items in that year = 4,05,265
Question 16.
India’s population has been steadily increasing from 439 million in 1961 to 1028 million in 2001. Find the total increase in population from 1961 to 2001. Write the increase in population in the Indian system of Numeration using commas suitably.
Solution:
Population of India in 1961 = 439 millions = 439,000,000
Population of India in 2001 = 1028 millions = 1,028,000,000
Increase in population from 1961 to 2001 = Population in 2001 – Population in 1961
= 1028000000 – 439000000
= 589000000
= 589 million.
Increase in population in Indian System = 58,90,00,000
Question 17.
A person had ₹ 10,00,000 with him. He purchased a flat for ₹ 8,70,000. With the remaining money, he has to buy a T.V. for 1 lakh. How much money was left with him to buy a T.V?
Solution:
Total money the person had = ₹ 10,00,000
Cost of flat = ₹ 8,70,000
Remaining money = ₹ 1,30,000
Now he has ₹ 1,30,000. So it is enough to buy a TV for ₹ 1,00,000.
Question 18.
A box contains 50 packets of biscuits, each weighing 120g. How many such boxes can be loaded in a van, which cannot carry more than 900 kg?
Solution:
Given: Total number of packets = 50.
Weight of each packet = 120 g
Weight of a box = 50 × 120 g = 6000 g = 6 kg [∵ 1000 g = 1 kg]
Required number of boxes = \(\frac{900}{6}\) = 150.
150 boxes are required.
Question 19.
How much money was collected from 5342 students for a charity show, if each student contributed ₹ 670?
Solution:
Total number of students = 5342
Contribution of each student = ₹ 670
Total money collected = 5342 × 670 = ₹ 35,79,140
Total money collected = ₹ 35,79,140
Question 20.
Estimate the following to the nearest hundreds
(a) 439 + 334 + 4317
(b) 1,08,734 – 47,599
(c) 8325 – 491
(d) 4,89,348 – 48,365
Solution:
(a) 439 + 334 + 4317
439 ⇒ 400
334 ⇒ 300
4317 ⇒ 4300
Sum = 5,000
(b) 1,08,734 – 47,599
1,08,734 ⇒ 1,08,700
47,599 ⇒ 47,600
Difference = 61,100
(c) 8325 – 491
8325 ⇒ 8300
491 ⇒ 500
Differences = 7,800
(d) 4,89,348 – 48,365
4,89,348 ⇒ 4,89,300
48,365 ⇒ 48,400
Difference = 4,40,900
![]()
Question 21.
Estimate the following products:
(a) 578 × 161
(b) 5281 × 3491
(c) 1291 × 592
(d) 9250 × 29
Solution:
(a) 578 × 161
578 ⇒ 600
161 ⇒ 200
Estimated product is 600 × 200 = 1,20,000
(b) 5281 × 3491
5281 ⇒ 5000
3491 ⇒ 3500
Estimated Product = 5000 × 3500 = 1,75,00,000
(c) 1291 × 592
1291 ⇒ 1300
592 ⇒ 600
Estimated Product is = 1300 × 600 = 7,80,000
(d) 9250 × 29
9250 ⇒ 9000
29 ⇒ 30
Estimated Product is 9000 × 30 = 2,70,000
Question 22.
Are all whole numbers are natural numbers? Justify your answer?
Solution:
No, all whole numbers are not natural numbers.
Because ‘0’ belongs to the whole number system. But it is not in a natural number system.
All whole numbers except ‘0’ are natural numbers.
Question 23.
Use associative property of addition to add 847 + 306 + 453
Solution:
847 + 306 + 453
= (847 + 453) + 306
= 1300 + 306
= 1606
∴ 847 + 306 + 453 = 1606
Question 24.
Find the value of (1063 × 127) – (1063 × 27)
Solution:
(1063 × 127) – (1063 × 27)
= 1063 (127 – 27) [Taking 1063 as common]
= 1063 × 100
= 106300.
i.e (1063 × 127) – (1063 × 27) = 106300
Question 25.
Find the product using suitable properties
(a) 738 × 103
(b) 1005 × 168
Solution:
(a) We have 738 × 103
= 738 × (100 + 3)
= 738 × 100 + 738 × 3 [By distributive property of multiplication over addition]
= 73800 + 2214
= 76014
(b) 1005 × 168
= (1000 + 5) × 168
= (168 × (1000 + 5) (By commutative property)
= (168 × 1000) + (168 × 5)
= 1,68,000 + 840
= 1,68,840
![]()
Question 26.
Write the largest six-digit number and write the number names in words using the Indian and International system.
Solution:
The largest six-digit number is 999999
Number names are nine lakh ninety-nine thousand nine hundred and ninety-nine
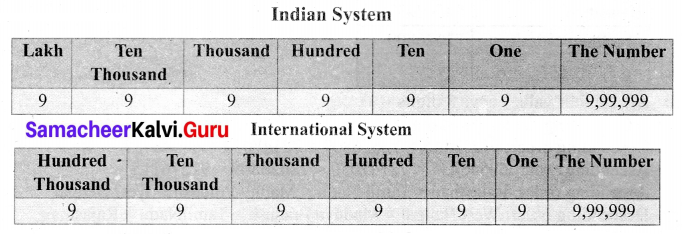
Question 27.
In a mobile store, the number of mobiles sold during a month is 1250, Assuming that the same number of mobiles are sold every month, find the number of mobiles sold in 2 years.
Solution:
Number of mobiles sold in 1 month = 1250
1 year = 12 months
2 years = 2 × 12 = 24 months
Number of mobiles sold in 24 months = 1250 × 24= 30,000
Number of mobiles sold in 2 years = 30,000
Question 28.
Simplify 24 + 2 × 8 ÷ 2 – 1
Solution:
24 + 2 × 8 ÷ 2 – 1
= 24 + 2 × 4 – 1
= 24 + 8 – 1
= 32 – 1
= 31
![]()