You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 2 Real Numbers Ex 2.6
Question 1.
Simplify the following using addition and subtraction properties of surds:
(i) 5\(\sqrt { 3 }\) + 18\(\sqrt { 3 }\) – 2\(\sqrt{3}\)
(ii) 4\(\sqrt [ 3 ]{ 5 }\) + 2\(\sqrt [ 2 ]{ 5 }\) – 3\(\sqrt [ 3 ]{ 5 }\)
(iii) 3\(\sqrt { 75 }\) + 5\(\sqrt { 48 }\) – \(\sqrt { 243 }\)
(iv) 5\(\sqrt [ 3 ]{ 40 }\) + 2\(\sqrt [ 3 ]{ 625 }\) – 3\(\sqrt [ 3 ]{ 320 }\)
Solution:
(i) 5\(\sqrt { 3 }\) + 18\(\sqrt { 3 }\) – 2\(\sqrt { 3 }\) = (5 + 18 – 2)\(\sqrt { 3 }\) = 21\(\sqrt { 3 }\)
(ii) 4\(\sqrt [ 3 ]{ 5 }\) + 2\(\sqrt [ 2 ]{ 5 }\) – 3\(\sqrt [ 3 ]{ 5 }\) = (4 + 2 – 3)\(\sqrt [ 3 ]{ 5 }\) = 3\(\sqrt [ 3 ]{ 5 }\)
(iii) 3\(\sqrt { 75 }\) + 5\(\sqrt { 48 }\) – \(\sqrt { 243 }\)

(iv) 5\(\sqrt [ 3 ]{ 40 }\) + 2\(\sqrt [ 3 ]{ 625 }\) – 3\(\sqrt [ 3 ]{ 320 }\)
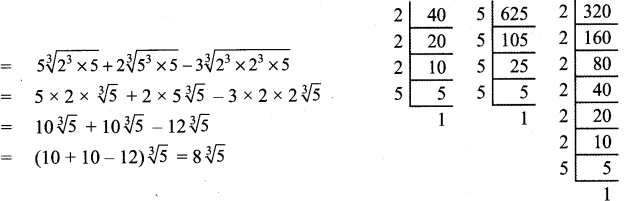
Question 2.
Simplify the following using multiplication and division properties of surds :
(i) \(\sqrt{3} \times \sqrt{5} \times \sqrt{2}\)
(ii) \(\sqrt { 35 }\) ÷ \(\sqrt { 7 }\)
(iii) \( \sqrt[3]{27} \times \sqrt[3]{8} \times \sqrt[3]{125}\)
(iv) (7\(\sqrt { a }\) – 5\(\sqrt { b }\))(7\(\sqrt { a }\) + 5\(\sqrt { b }\))
(v) \([\sqrt{\frac{225}{729}}-\sqrt{\frac{25}{144}}] \div \sqrt{\frac{16}{81}}\)
Solution:

Question 3.
If \(\sqrt { 7 }\) =1.414, \(\sqrt { 3 }\) = 1.732, \(\sqrt { 5 }\) = 2.236, \(\sqrt { 10 }\) = 3.162, then find the values of the following correct to 3 places of decimals.
(i) \(\sqrt{40}-\sqrt{20}\)
(ii) \(\sqrt{300}+\sqrt{90}-\sqrt{8}\)
Solution:
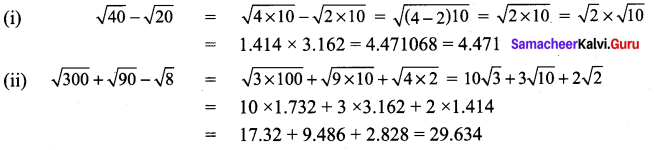
![]()
Question 4.
Arrange surds in descending order :
(i) \(\sqrt[3]{5}, \sqrt[9]{4}, \sqrt[6]{3}\)
(ii) \(\sqrt[2]{\sqrt[3]{5}}, \sqrt[3]{\sqrt[4]{7}}, \sqrt{\sqrt{3}}\)
Solution:
(i) \(\sqrt[3]{5}, \sqrt[9]{4}, \sqrt[6]{3}\)
5\(\frac { 1 }{ 3 }\)
∴ The order of the surds \(\sqrt[3]{5}, \sqrt[9]{4}, \sqrt[6]{3}\) are 3, 9, 6.
4\(\frac { 1 }{ 9 }\)
3\(\frac { 1 }{ 6 }\) l.c.m of 3, 9, 6 is 18
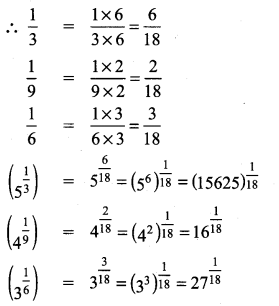
∴ The descending order of \(\sqrt[3]{5}, \sqrt[9]{4}, \sqrt[6]{3}\) is \((15625)^{\frac{1}{18}}>(27)^ {\frac{1}{18}} >16^{\frac{1}{18}} \text { i.e. } \sqrt[3]{5}>\sqrt[6]{3}>\sqrt[9]{4}\)
(ii) \(\sqrt[2]{\sqrt[3]{5}}, \sqrt[3]{\sqrt[4]{7}}, \sqrt{\sqrt{3}}\)
The order of the surds \(\sqrt[2]{\sqrt[3]{5}}, \sqrt[3]{\sqrt[4]{7}}, \sqrt{\sqrt{3}}\) are 6, 12, 4
l.c.m of 6, 12, 4 is 12

Question 5.
Can you get a pure surd when you find
(i) the sum of two surds
(ii) the difference of two surds
(iii) the product of two surds
(iv) the quotient of two surds
Justify each answer with an example.
Solution:
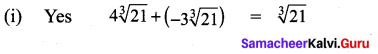
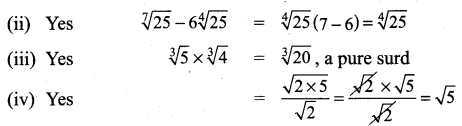
Question 6.
Can you get a rational number when you compute
(i) the sum of two surds
(ii) the difference of two surds
(iii) the product of two surds
(iv) the quotient of two surds
Justify each answer with an example.
Solution:
(i) Yes (5 – \(\sqrt{3}\)) + (5 + \(\sqrt{3}\)) = 10, a rational number
(ii) Yes \((5+\sqrt[3]{7})-(-6+\sqrt[3]{7})=11\), a rational number
(iii) Yes (5 + \(\sqrt{3}\) ) (5 – \(\sqrt{3}\) ) = 25 – 3 = 22, a rational number
(iv) Yes \(\frac{5 \sqrt{3}}{\sqrt{3}}=5\) ,a rational number