Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.6

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.6

Question 1.
Find a parametric form of vector equation of a plane which is at a distance of 7 units from the origin having 3, -4, 5 as direction ratios of a normal to it.
Solution:
Given p = 7

Question 2.
Find the direction cosines of the normal to the plane 12x + 3y – 4z = 65. Also, find the non-parametric form of vector equation of a plane and the length of the perpendicular to the plane from the origin.
Solution:
12x + 3y – 4z = 65

(iii) Length of the perpendicular to the plane from the origin is 5 units.

Question 3.
Find the vector and Cartesian equation of the plane passing through the point with position vector \(2 \hat{i}+6 \hat{j}+3 \hat{k}\) and normal to the vector \(\hat{i}+3 \hat{j}+5 \hat{k}\)
Solution:

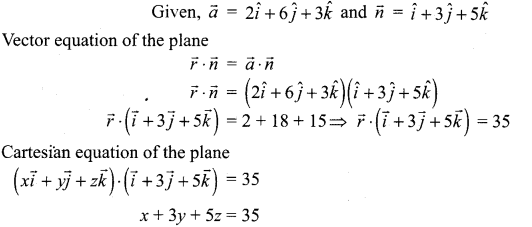
Question 4.
A plane passes through the point (-1, 1, 2) and the normal to the plane of magnitude \(3 \sqrt{3}\) makes equal acute angles with the coordinate axes. Find the equation of the plane.
Solution:
Given magnitude = \(3 \sqrt{3}\) and \(\vec{a}=-\vec{i}+\vec{j}+2 \vec{k}\)
Then, the normal vector makes an equal acute angle with the coordinate axes.
We know that cos² α + cos² β + cos² γ = 1 (But α = β = γ)

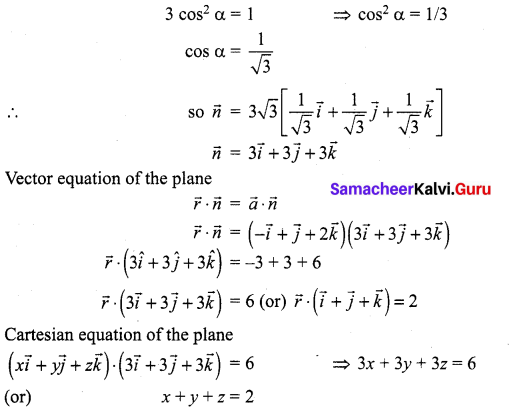
Question 5.
Find the intercepts cut off by the plane \(\vec{r} \cdot(6 \hat{i}+4 \hat{j}-3 \hat{k})\) = 12 on the coordinate axes.
Solution:

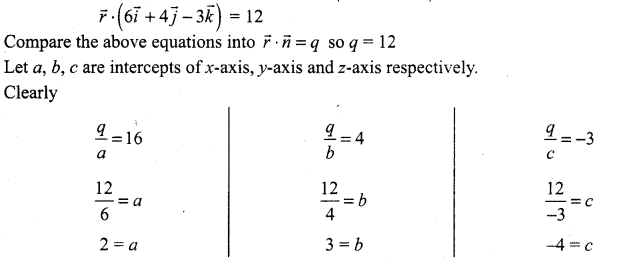
x-intercept = 2; y-intercept = 3; z-intercept = -4

Question 6.
If a plane meets the coordinate axes at A, B, C such that the centroid of the triangle ABC is the point (u, v, w), find the equation of the plane.
Solution:
Let A (a, 0, 0), B(0, b, 0), C(0, 0, c)
centroid of ∆ABC = \(\left(\frac{a}{3}, \frac{b}{3}, \frac{c}{3}\right)\)

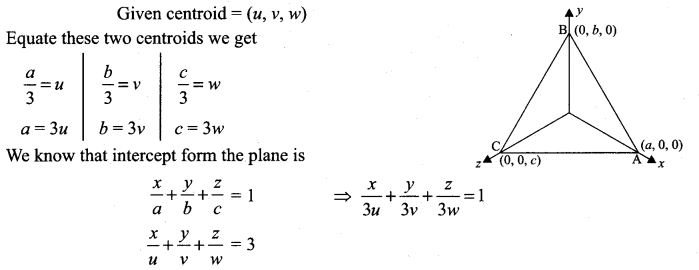
Samacheer Kalvi 12th Maths Solutions Chapter 6 Applications of Vector Algebra Ex 6.6 Additional Problems

Question 1.
Find the vector and cartesian equations of a plane which is at a distance of 18 units from the origin and which is normal to the vector \(2 \vec{i}+7 \vec{j}+8 \vec{k}\)
Solution:

Question 2.
Find the unit vector to the plane 2x – y + 2z = 5.
Solution:
Writing the plane in normal form we get,

Question 3.
Find the length of the perpendicular from the origin to the plane \(\vec{r} \cdot(3 \vec{i}+4 \vec{j}+12 \vec{k})\) = 26.
Solution:
Taking the equation of the plane in cartesian form we get,
\((x \vec{i}+y \vec{j}+z \vec{k}) \cdot(3 \vec{i}+4 \vec{j}+12 \vec{k})\) = 26
i.e., 3x + 4y+ 12z – 26 = 0
The length of the perpendicular from (0, 0, 0) to the above plane is
\(\pm \frac{-26}{\sqrt{9+16+144}}=\frac{+26}{13}\) = 2 units

Question 4.
The foot of the perpendicular drawn from the origin to a plane is (8, -4, 3). Find the equation of the plane.
Solution:
The required plane passes through the point A(8, -4, 3) and is perpendicular to \(\overrightarrow{\mathrm{OA}}\) .

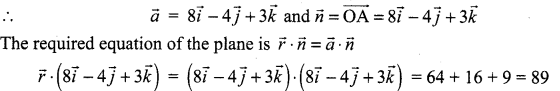
The cartesian equation is 8x – 4y + 3z = 89.

Question 5.
Find the equation of the plane through the point whose position vector is \(2 \vec{i}-\vec{j}+\vec{k}\) and perpendicular to the vector \(4 \vec{i}+2 \vec{j}-3 \vec{k}\).
Solution:
The required plane is perpendicular to \(4 \vec{i}+2 \vec{j}-3 \vec{k}\)
So, it is parallel to the plane 4x + 2y – 3z = k
∴ the equation of the plane is 4x + 2y – 3z = k
The plane passes through the point (2, -1, 1)
⇒ (4)(2) + 2(-1) – 3(1) = λ i.e. λ = 8 – 2 – 3 = 3
So, the equation of the plane is 4x + 2y – 3z = 3.

Question 6.
Find the vector and cartesian equations of the plane passing through the point (2, -1, 4) and parallel to the plane \(\vec{r} \cdot(4 \vec{i}-12 \vec{j}-3 \vec{k})\) = 7.
Solution:
The given plane is \(\vec{r} \cdot(4 \vec{i}-12 \vec{j}-3 \vec{k})\) = 7
i e. \((x \vec{i}+y \vec{j}+z \vec{k}) \cdot(4 \vec{i}-12 \vec{j}-3 \vec{k})\) = 7
i.e. 4x – 12y – 3z = 1
The required plane is parallel to the above plane. So, the equation of the required plane is 4x – 12y – 3z – k. The plane passes through (2, -1, 4).
⇒ 4(2) – 12(-1) – 3(4) = k i.e. k = 8 + 12 – 12 = 8
So, the equation of the plane is 4x – 12y – 3z = 8.