Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.1

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.1

Question 1.
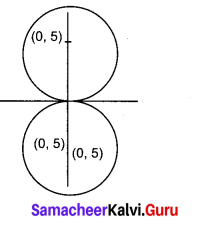
Obtain the equation of the circles with radius 5 cm and touching x-axis at the origin in general form.

Solution:
Radius = 5 cm
Passing through the point (0, 0)
Centre of y axis be (0, k)
Equation of circle be
(x – h)² + (y – k)² = r²
At (0, 0) ⇒ (x – 0)² + (y – k)² = r² = 5²
x² + (y – k)² = 25
0 + (0 – k)² = 25
k² = 25
k = ±5
(0, k) = (0, ± 5)
∴ (1) ⇒ (x – 0)² + (y ± 5)² = r²
x² + y² ± 10y + 25 = 25
x² + y² ± 10y = 0

Question 2.
Find the equation of the circle with center (2, -1) and passing through the point (3, 6) in standard form.
Solution:
Centre = C = (2, -1); Passing through = A = (3, 6)
So radius = CA = \(\sqrt{(2-3)^{2}+(-1-6)^{2}}=\sqrt{1+49}=5 \sqrt{50}\)
Now centre = (2, -1) and radius = \(\sqrt{50}\)
So equation of the circle is
(i.e) (x – 2)² + (y + 1)² = \(\sqrt{50}^{2}\) ⇒ (x – 2)² + (y + 1)² = 50

Question 3.
Find the equation of circles that touch both the axes and pass-through (-4, – 2) in a general form.
Solution:
centre (h, k), radius r
(x – h)² + (y – k)² = r²
(x – r)² + (y – r}² = r²
At (-4, -2)
(-4 – r)² + (- 2 – r)² = r²
4² + r² + 8r + 4 + r² + 4r = r²
r² + 12r + 20 = 0
(r + 10) (r + 2) = 0
r = -10; r = -2
(i) r = -2
(x + 2)² + (y + 2)² = -2²
x² + 4x + 4+ y² + 4y + 4 = 4
x² + y² + 4x + 4y + 4 = 0

(ii) r = -10
(x + 10)² + (y + 10)² = -10²
x² + 100 + 20x + y² + 20y + 100 = 100
x² + y² + 20x + 20y + 100 = 0

Question 4.
Find the equation of the circle with centre (2, 3) and passing through the intersection of the lines 3x – 2y -1 = 0 and 4x + y – 27 = 0 .
Solution:
To find the point of intersection of the two lines we have to solve the two equations.
Now solving them: 3x — 2y = 1 ……….. (1)
4x + y = 27 ……….(2)
(2) × 2 ⇒ 8x + 2y = 54 ……….. (3)
(1) ⇒ 3x – 2y = 1 ………. (1)
(3) + (1) ⇒ 11x = 55 ⇒ x = \(\frac{55}{11}\) = 5
Substituting x = 5 in (2) we get
20 + y = 27 ⇒ y = 27 – 20 = 7
∴ The point = A = (5, 7)
Given centre = C = (2, 3)
∴ radius = \(\sqrt{(5-2)^{2}+(7-3)^{2}}=\sqrt{9+16}=5\) = 5
Now centre = (2, 3) and radius = 5
So equation of the circle is
(x – 2)² + (y – 3)² = 5²
(i.e) x² + y² – 4x – 6y – 12 =0

Question 5.
Obtain the equation of the circle for which (3, 4) and (2, -7) are the ends of a diameter.
Solution:
The equation of a circle with (x₁ , y₁) and (x₂ , y₂ ) as end points of a diameter is
(x₁, y₁) = (3, 4), (x₂, y₂) = (2, -7)
(x – x₁) (x – x₂) + (y – y₁) (y – y₂) = 0
(x – 3) (x – 2) + (y – 4) (y + 7) = 0
x² – 5x + 6 + y² + 3y – 28 = 0
x² + y² – 5x + 3y – 22 = 0

Question 6.
Find the equation of the circle through the points (1, 0), (-1, 0), and (0, 1).
Solution:
Let the required circle be
x² + y² + 2gx + 2fy + c = 0 …………. (A)
The circle passes through (1, 0), (-1, 0) and (0, 1)
(1, 0) ⇒ 1 + 0 + 2g(1) + 2f(0) + c = 0
2g + c = -1 ……………. (1)
(-1, 0) ⇒ 1 + 0 + 2g (-1) + 2f(0) + c = 0
-2g + c = -1 ……….. (2)
(0, 1) ⇒ 0 + 1 + 2g (0) + 2f(1) + c = 0
2f+ c = -1 ……….. (3)
Now solving (1), (2) and (3) .
2g + c = -1 ………… (1)
-2g + c = -1 ………….. (2)
(1) + (2) ⇒ 2c = -2 ⇒ c = -1
Substituting c = -1 in (1) we get
2g – 1 = -1
2g = -1 + 1 = 0 ⇒ g = 0
Substituting c = -1 in (3) we get
2f – 1 =-1 ⇒ 2f = -1 + 1 = 0 ⇒ f = 0
So we get g = 0, f= 0 and c = -1
So the required circle will be
x² + y² + 2(0) x + 2(0)y – 1 = 0
(i.e) x² + y² – 1 = 0 ⇒ x² + y² = 1

Question 7.
A circle of area 9n square units has two of its diameters along the lines x + y = 5 and x – y = 1. Find the equation of the circle.
Solution:
Area of a circle πr² = 9π
r² = 9
solve: x + y = 5 ……….. (1)
x – y = 1 ……….. (2)
We get centre of the circle.
Add (1) and (2) ⇒ 2x = 6
x = 3
(1) ⇒ 3 + y = 5
y = 2
Centre (h, k) = (3, 2) and r² = 9
(x – h)² + (y – k)² = r²
(x – 3)² + (7 – 2)² = 9
x² + 9 – 6x + y² – 4y + 4 = 9
x² + y² – 6x – 4y + 4 = 0

Question 8.
If y = \(2 \sqrt{2} x\) + c is a tangent to the circle x² + y² =16 , find the value of c .
Solution:
The condition for the line y = mx + c to be a tangent to the circle x² + y² = a² is
c² = a²(1 + m²)
Here x² + y² = 16 ⇒ a² = 16
y = \(2 \sqrt{2} x\) + c ⇒ m = \(2 \sqrt{2}\) and c = c
The condition is c² = a² (1 + m²)
(i.e) c² = 16(1 + 8) = 144
⇒ c = ± 12

Question 9.
Find the equation of the tangent and normal to the circle x² + y² – 6x + 6y – 8 = 0 at (2, 2).
Solution:
Equation of the tangent be
xx₁ + yy₁ – 6(\(\frac {x+x_1}{2}\)) + 6(\(\frac {y+y_1}{2}\)) – 8 = 0
At (2, 2)
2x + 2y – 3 (x + 2) + 3 {y + 2) – 8 = 0
2x + 2y – 3x – 6 + 3y + 6 – 8 = 0
-x + 5y – 8 = 0
x – 5y + 8 = 0
Equation of the normal be
yx₁ – xy₁ + g(y – y₁) -f(x – x₁) = 0
2g = -6, 2f = 6
g = -3, f = 3
At (2, 2)
y(2) – x(2) – 3 (y – 2) – 3(x – 2) = 0
2y – 2x – 3y + 6 – 3x + 6 = 0
– 5x – y + 12 = 0
5x + y – 12 = 0
Another method for Normal
Equation of tangent is perpendicular to normal
x – 5y + 8 = 0
Perpendicular equation be 5x + y + k = 0
At (2, 2) 10 + 2 + k = 0
k = -12
∴ 5x + y – 12 = 0 be equation of normal.

Question 10.
Determine whether the points (-2, 1), (0, 0) and (-4, -3) lie outside, on or inside the circle x² + y² – 5x + 2y – 5 = 0 .
Solution:
To find the position of a point with regard to a given circle, substitute the point in the equation of the circle if we get a positive value, the point lies outside the circle.
If we get a -ve value the point lies inside the circle and if we get O then the point lies on the circumference of the circle.
The given circle is x² + y² – 5x + 2y – 5 = 0 ……….. (1)
Substituting the point (-2, 1) in (1) we get
4 + 1 – 5(-2) + 2(1) – 5 = 5 + 10 + 2 – 5 = 12
⇒ (- 2, 1) lies outside the circle
Substituting the point (0, 0) in (1) we get
-5 < 0 ⇒ (0, 0) lies inside the circle Substituting the point (-4, -3) in (1) we get 16 + 9 + 20 – 6 – 5 = 34 >0
⇒ (- 4, -3) lies outside the circle

Question 11.
Find centre and radius of the following circles.
(i) x² + (y + 2)² = 0
(ii) x² + y² + 6x – 4y + 4 = 0
(iii) x² + y² – x + 2y – 3 = 0
(iv) 2x² + 2y² – 6x + 4y + 2 = 0
Solution:
(i) x² + (y + 2)² = 0
Compare with (x – h)² + (y – k)² = r²
h = 0, k = -2, r² = 0
Centre (h, k) = (0, – 2)
r = 0 = radius

(ii) x² + y² + 6x – 4y + 4 = 0
2g = 6; 2f = -4; c = 4
g = 3 f = -2
Centre (-g, -f) = (-3, 2)
Radius r = \(\sqrt{g^2+f^2-c}\) = \(\sqrt{9+4-4}\) = 3

(iii) x² + y² – x + 2y – 3 = 0
Comparing with the general form of the circle we get

(iv) 2x² + 2y² – 6x + 4y + 2 = 0
(÷2) x² + y² – 3x + 2y + 1 = 0
2g = -3; 2f = 2; c = 1
g = \(\frac{-3}{2}\), f = 1, c = 1
centre (-g, -f) = (\(\frac{3}{2}\), -1)
r = \(\sqrt{g^2+f^2-c}\) = \(\sqrt{\frac{9}{4}+1-1}\) = \(\frac{3}{2}\)

Question 12.
If the equation 3x² + (3 -p) xy + qy² – 2px = 8 pq represents a circle, find p and q. Also determine the centre and radius of the circle.
Solution:
For a circle co-eff of x² = co-efif of y²
⇒ 3 = q
co-eff of xy = 0
⇒ 3 – p = 0 ⇒ p = 3
So p = q = 3
So the equation of the circle becomes 3x² + 3y² – 6x – 72 = 0
(÷ by 3) ⇒ x² + y² – 2x – 24 = 0
Comparing this equation with the general form of the circle we get
2g = -2, 2f = 0
g = -1, f = 0 and c = -24
So centre = (-g, -f) = (1, 0) and radius = \(\sqrt{g^{2}+f^{2}-c}\) = 5
∴ Centre =(1,0) and radius = 5

Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.1 Additional Problems

Question 1.
Find the equation of the circle whose centre is (2, -3) and passing through the intersection of the line 3x – 2y = 1 and 4x + y = 27.
Solution:
Solving 3x – 2y = 1 and 4x+y = 27
Simultaneously, we get x = 5 and y = 7
∴ The point of intersection of the lines is (5, 7)

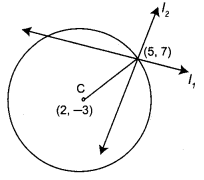
Now we have to find the equation of a circle whose centre is (2, -3) and which passes through (5,7)

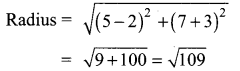
∴ Required equation of the circle is
(x – 2)² + (y + 3)² = \((\sqrt{109})^{2}\)
⇒ x² + y² – 4x + 6y – 96 = 0

Question 2.
Find the equation of a circle of radius 5 whose centre lies on the x-axis and which passes through the point (2, 3).
Solution:
Let the centre of the circle be (h, k). Since the centre lies on the x-axis, we have k = 0
Therefore, centre = (h, 0)
Also, the circle has radius 5 units and passes through the point (2, 3).

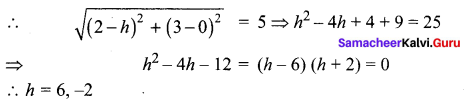
Hence the centre is (6, 0) or (-2, 0)
∴ The equation of the circle is
(x – 6)² + (y – 0)² = 5² ⇒ x² + y² – 12x+ 11 = 0 (Or) (x + 2)² + (y – 0)² = 5² ⇒ x² + y² + 4x – 21 =0

Question 3.
Find the centre and radius of the following circles:
x² + y² – 2x + 4y – 4 = 0 and 2x² + 2y² + 16x – 28y + 32 = 0. Also find the ratio of their diameters.
Solution:
Comparing the equation x² + y² – 2x + 4y – 4 = 0 with x² + y² + 2gx + 2 fy + c = 0, we get
2g = -2 ⇒ g = -1, 2f = 4 ⇒ f = 2, c = -4

Comparing with x² + y² + 2gx + 2fy + c = 0
2g = 8 ⇒ g = 4, 2f = -14 ⇒ f = -7, c = 16

Diameter = 2r₂ = 2 × 7 = 14 units
Ratio of their diameters = 6 : 14 = 3 : 7.

Question 4.
Find the equation of the circle whose radius is 4 and which is concentric with the circle x² + y² + 2x – 6y = 0
Solution:
x² + y² + 2x – 6y = 0 …(1)
Here 2g = 2 ⇒ g = 1, 2f = -6 ⇒ f = -3
Centre of the circle = (-g, -f) = (-1, 3)
Since the required circle is concentric with (1), its centre is also (-1, 3).
∴ The equation of the circle whose centre is (-1, 3) and radius 4 is
(x + 1)² + (y – 3)² = 4²
⇒ x² + y² + 2x – 6y – 6 = 0

Question 5.
Show that the four points (1, 0), (2, -7), (8,1) and (9, 6) are concyclic.
Solution:
Let the equation of the circle be Since it passes through (1, 0)
⇒ x² + y² + 2gx + 2fy + c = 0 …(1)

Question 6.
Find the equation of a circle which passes through the points (1, -2) and (4, -3) and whose centre lies on the line 3x + 4y = 0
Solution:
Let the equation of the circle be
x² + y² + 2gx + 2fy + c = 0 …(1)
Since it passes through (1, -2) and (4, -3)
∴ 5 + 2g – 4f + c = 0 …(2)
and 25 + 8g – 6f + c = 0 …(3)
Also (-g, -f) centre of circle (1) lies on 3x + 4y = 7
-3g – 4f = 7 …(4)
Subtracting (2) from (3), we get
20 + 6g – 2f = 0 …(5)
Solving (4) and (5), we get

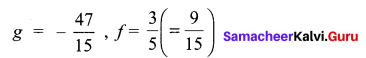
Substituting these values of g and f in (2)

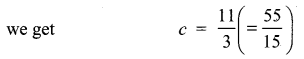
∴ From (1), we get,

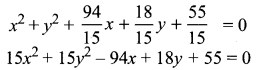
Which is the required equation on the circle.

Question 7.
Find the equation (s) of the circle passing through the points (1, 1) and (2, 2) and whose radius is 1.
Solution:
Let the equation of the circle be
x² + y² + 2gx + 2fy + c = 0 …. (1)
Since it passes through (1,1)
∴ 1 + 1 + 2g + 2f + c = 0
⇒ 2g + 2f + c + 2 = 0 ….(2)
Again it passes through (2, 2)
∴ 4 + 4+ 4g + 4f + c = 0
⇒ 4g + 4f + c + 8 = 0 …(3)

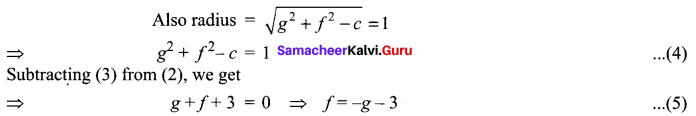
Adding (2) and (4)
g² + 2g + f² + 2f + 2 = 1
g² + 2g + (-g – 3)² + 2(-g – 3) + 1 = 0
⇒ 2g² + 6g + 4 = 0 ⇒ g² + 3g + 2 = 0
⇒ (g + 1)(g + 2) = 0 ⇒ g = -1, -2
when g = -1, from (5), f = – (-1) – 3 = 1 – 3 = -2
when g = -2, from (5), f = – (-2) – 3 = 2 – 3 = -1
Substituting g = -1, f = -2 in (2), we get
2(-1) + 2(-2) + c + 2 =0
⇒ – 6 + c + 2 = 0 ⇒ c = 4
Now putting g = -1, f = -2 and c = 4 in (1), we get
x² + y² – 2x – 4y + 4 = 0
Again putting g = -2, f = -1 in (2), we get
2(-2) + 2(-1) + c + 2 =0
⇒ -4 – 2 + c + 2 =0 ⇒ c = 4
Putting g = -2, f = -1 and c = 4 (in) (1), we get
x² + y² – 4x – 2y + 4 = 0
Hence the required equation (s) of the circle are
x² + y² – 2x – 4y + 4 =0 and x² + y² – 4x – 2y + 4 = 0.