You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 12 Discrete Mathematics Ex 12.2
Question 1.
Let p : Jupiter is a planet and q : India is an island be any two simple statements. Give verbal sentence describing each of the following statements.
![]()
Solution:
(i) \(\neg p\) : Jupiter is not a planet
(ii) \(p \wedge \neg q\) : Jupiter is not a planet and India is not an island
(iii) \(\neg p \vee q\) : Jupiter is not a planet or India is an island.
(iv) \(p \rightarrow \neg q\) : If Jupiter is a planet then India is not an island
(v) \(p \leftrightarrow q\) : If Jupiter is a planet if and only if India is an island
Question 2.
Write each of the following sentences in symbolic form using statement variables p and q.
(i) 19 is not a prime number and all the angles of a triangle are equal.
(ii) 19 is a prime number or all the angles of a triangle are not equal
(iii) 19 is a prime number and all the angles of a triangle are equal
(iv) 19 is not a prime number
Solution:
p : 19 is a prime number
q : All the angles of a triangle are equal
![]()
![]()
Question 3.
Determine the truth value of each of the following statements
(i) If 6 + 2 = 5 , then the milk is white.
(ii) China is in Europe or \(\sqrt{3}\) is an integer
(iii) It is not true that 5 + 5 = 9 or Earth is a planet
(iv) 11 is a prime number and all the sides of a rectangle are equal
Solution:

Question 4.
Which one of the following sentences is a proposition?
(i) 4 + 7 = 12
(ii) What are you doing?
(iii) 3n ≤ 81, n ∈ N
(iv) Peacock is our national bird
(v) How tall this mountain is!
Solution:
(i) 4 + 7 = 12
It is a proposition as its truth value is F
(ii) What are you doing?
It is a question and not a proposition.
(iii) 3ⁿ ≤ 81, n ∈ N
It is a proposition as it is true when,
n = 1, 2, 3, 4
(iv) Peacock is our national bird. It is a proposition as its truth value is T.
(v) How tall this mountain is!
This is an exclamation, not a proposition
Question 5.
Write the converse, inverse, and contrapositive of each of the following implication.
(i) If x and y are numbers such that x = y, then x2 = y2
(ii) If a quadrilateral is a square then it is a rectangle
Solution:
(i) If x and y are numbers such that x = y, then x² = y²
Convene: If x and y are numbers such that x² = y² then x = y
Inverse: If x and y are numbers such that x ≠ y then x² ≠ y²
Contrapositive: If x and y are numbers such that x² ≠ y² then x ≠ y
(ii) If a quadrilateral is a square then it is a rectangle
Converse: If a quadrilateral is a rectangle then it is a square.
Inverse: If a quadrilateral is not a square then it is not a rectangle.
Contrapositive: If a quadrilateral is not a rectangle then it is not a square.
![]()
Question 6.
Construct the truth table for the following statements.
![]()
Solution:
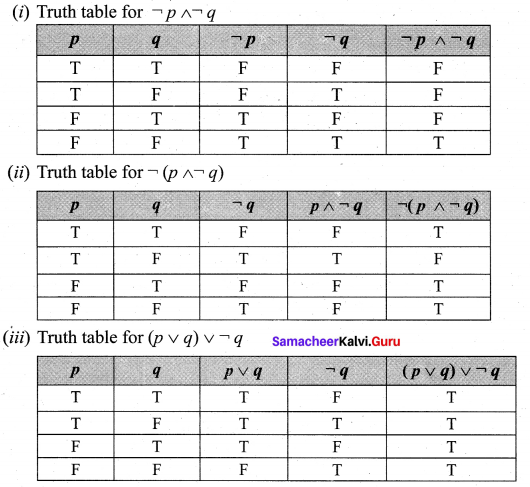
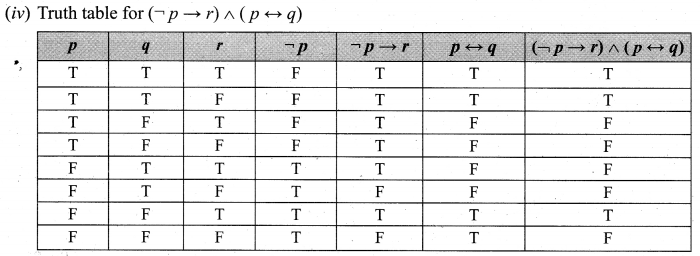
Question 7.
Verify whether the following compound propositions are tautologies or contradictions or contingency
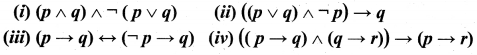
Solution:
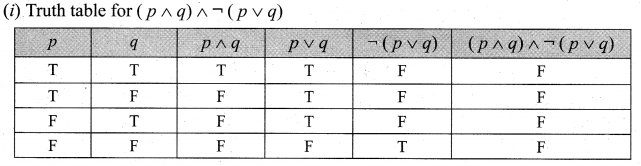
In the above Truth table the last column entries are ‘F’. So the given propositions is a contradiction.

In the above truth table, the last column entries are ‘T’. So the given proposition is a tautology.
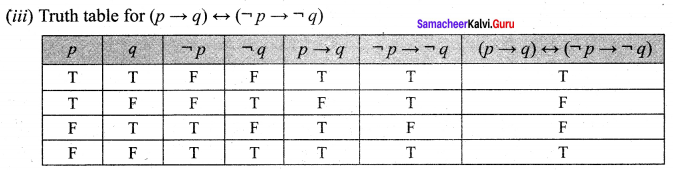
In the above truth table, the entries in the last column are a combination of’ T ‘ and ‘ F ‘.
So the given statement is neither propositions is neither tautology nor a contradiction. It is a contingency.
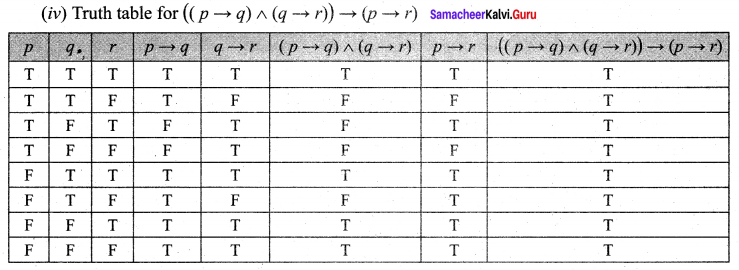
The last column entires are ‘T’. So the given proposition is a tautology.
![]()
Question 8.
![]()
Solution:
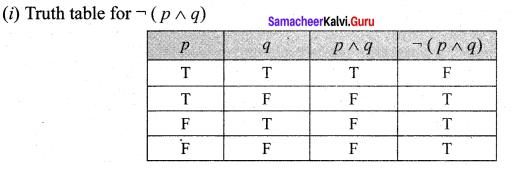
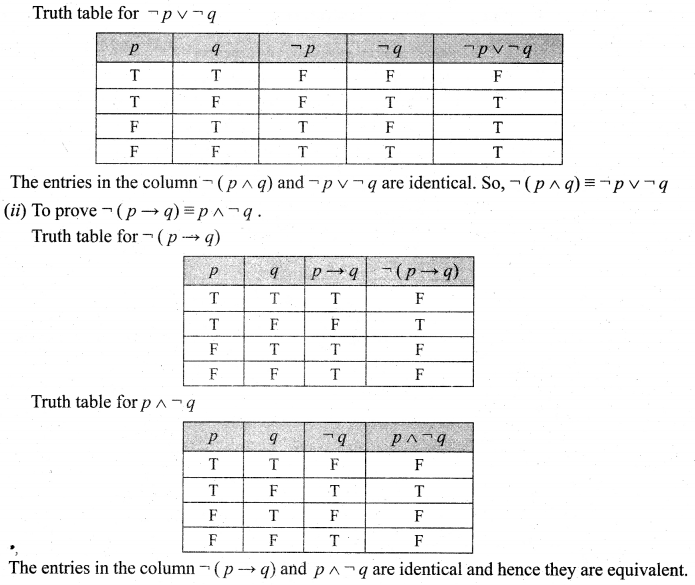
Question 9.
![]()
Solution:
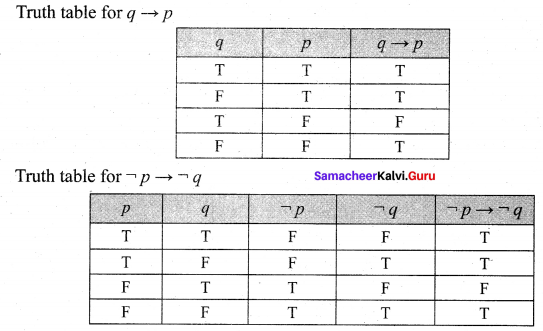
The entries in the column corresponding to q ➝ p and \(\neg p \rightarrow \neg q\) are identical and hence they are equivalent.
Question 10.
Show that p ➝ q and q ➝ p are not equivalent
Solution:
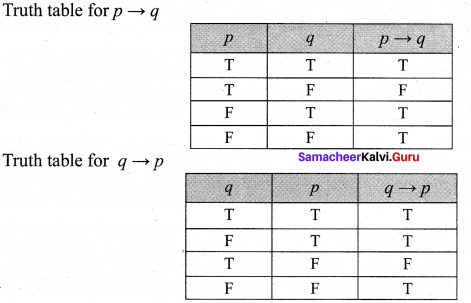
The entries in the column corresponding to p ➝ q and q ➝ p are not identical, hence they are not equivalent.
Question 11.
![]()
Solution:
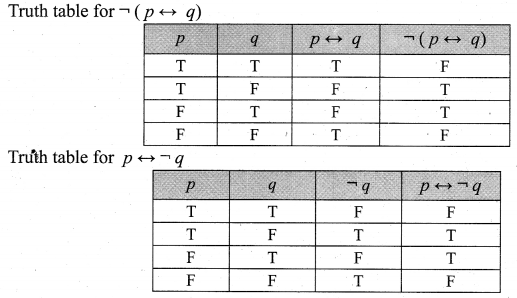
Question 12.
Check whether the statement p ➝ (q ➝ p) is a tautology or a contradiction without using the truth table.
Solution:

![]()
Question 13.
Using the truth table check whether the statements ![]() are logically equivalent.
are logically equivalent.
Solution:

Question 14.
![]() without using truth table
without using truth table
Solution:

Question 15.
![]()
Solution:
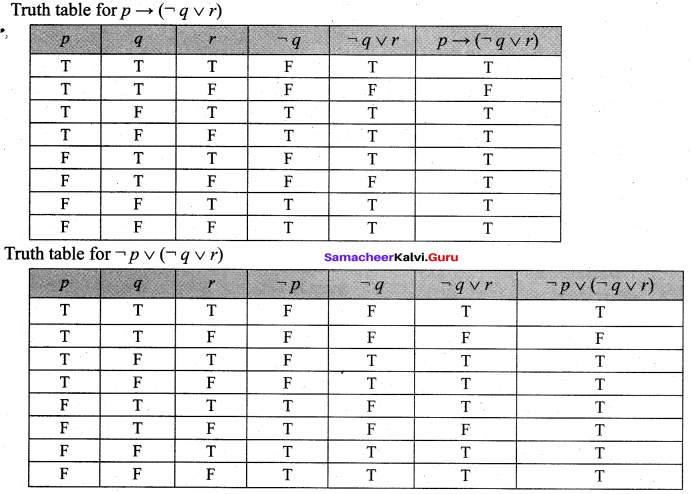
The entries in the column corresponding to ![]() are identical.
are identical.
Hence they are equivalent.
![]()
Samacheer Kalvi 12th Maths Solutions Chapter 12 Discrete Mathematics Ex 12.2 Additional Problems
Question 1.
Show that ![]() is a tautology.
is a tautology.
Solution:
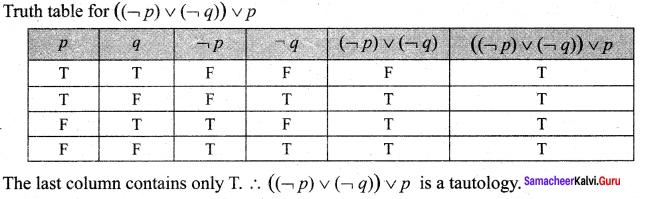
Question 2.
Show that ![]() is a contradiction.
is a contradiction.
Solution:

Question 3.
Use the truth table to determine whether the statement ![]() is a tautology.
is a tautology.
Solution:
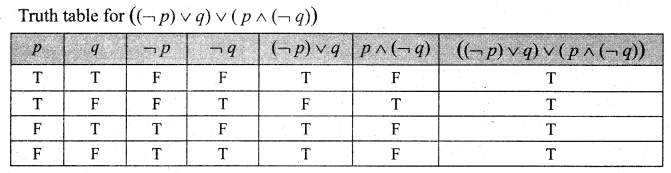
The last column contains only T. ∴ The given statement is a tautology.
Question 4.
Show that ![]()
Solution:
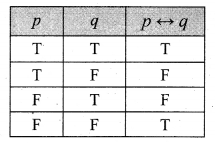
(i) Truth table for p \(\leftrightarrow\) q

![]()
Question 5.
Show that ![]() .
.
Solution:
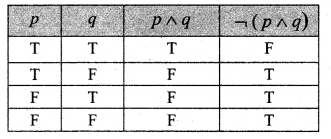
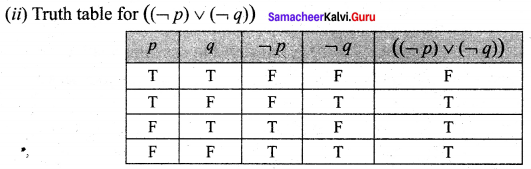
The last columns of statements (i) and (ii) are identical.
![]()