Students can Download Maths Chapter 4 Geometry Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 4 Geometry Intext Questions
Exercise 4.1
Try These (Text book Page No. 66)
Answer the following questions.
Question 1.
Triangle is formed by joining three ______ points.
Answer::
Non collinear
Question 2.
A triangle has ______ vertices and ______ sides.
Answer:
three, three
Question 3.
A point where two sides of a triangle meet is known as ______ of a triangle.
Answer:
vertese
![]()
Question 4.
Each angle of an equilateral triangle is of measure.
Answer:
same
Question 5.
A triangle has angle measurements of 29°, 65° and 86°. Then it is ______ triangle.
(i) an acute angled
(ii) a right angled
(iii) an obtuse angled
(iv) a scalene
Answer:
(i) an acute angled
Question 6.
A triangle has angle measurements of 30°, 30° and 120°. Then it is ______ triangle.
(i) an acute angled
(ii) scalene
(iii) obtuse angled
(iv) right angled
Answer:
obtuse angled
![]()
Question 7.
Which of the following can be the sides of a triangle?
(i) 5.9.14
(ii) 7,7,15
(iii) 1,2,4
(iv) 3, 6, 8
Answer:
(iv) 3, 6, 8
Solution:
(i) Here 5 + 9 = 14 = the measure of the third side.
In a triangle the sum of the measures of any two sides must be greater than the third side.
∴ 5, 9, 14 cannot be the sides of a triangle.
(ii) 7.7.15
Here sum of two sides 7 + 7 = 14 < the measures of the thrid side.
So 1,1, 15 cannot be the sides of a triangles.
(iii) 1,2,4
Here sum of two sides 1 + 2 = 3 < the measure of the third side.
∴ 1, 2, 4 cannot be the sides of a triangle.
(iv) 3, 6, 8
Sum of two sides 3 + 6 = 9 > the third side.
∴ 3, 6, 8 can be the sides of a triangle.
![]()
Question 8.
Ezhil wants to fence his triangular garden. If two of the sides measure 8 feet and 14 feet then the length of the third side is ______
(i) 11 ft
(ii) 6 ft
(iii) 5 ft
(iv) 22 ft
Answer:
(i) 11 ft
Question 9.
Can we have more than one right angle in a triangle?
Solution:
No, we cannot have more than one right angle in a triangle.
Because the sum of three angles of a triangle is 180°.
But if two angles are right angles then their sum itself become 180°.
![]()
Question 10.
How many obtuse angles are possible in a triangle?
Solution:
Only one.
Question 11.
In a right triangle, what will be the sum of other two angles?
Solution:
Sum of three angles of a triangle = 180°
If one angle is right angle (i.e. 90°) .
Sum of other two sides = 180° – 90° = 90°
Question 12.
Is it possible to form an isosceles right angled triangle? Explain.
Solution:
Yes, it is possible.
If one angle is right angle, then the other two angles will be 45° and 45°.
![]()
Exercise 4.2
Try These (Text book Page No. 76)
Question 1.
Measure and group the pair of congruent line segments.
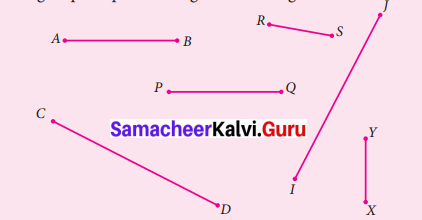
Solution:
\(\overline{A B}\) = 3 cm
\(\overline{C D}\) = 4.8 cm
\(\overline{I J}\) = 4.8 cm
\(\overline{P Q}\) = 3 cm
\(\overline{R S}\) = 1.7 cm
\(\overline{X Y}\) = 1.7 cm
From the above measurement S, we can conclude that
(i) \(\overline{A B}\) ≅ \(\overline{P Q}\)
(ii) \(\overline{C D}\) ≅ \(\overline{I J}\)
(iii) \(\overline{R S}\) ≅ \(\overline{X Y}\)
![]()
Try These (Text book Page No. 77)
Question 1.
Find the pairs of congruent angles either by superposition method or by measuring them.
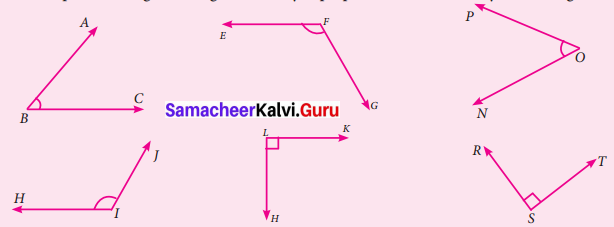
Solution:
From the given figures
∠ABC = 50°
∠EFG = 120°
∠HIJ = 120°
∠KLH = 90°
∠PON = 50°
∠RST = 90°
From the above measures, we can conclude that
(i) ∠ABC = ∠PON
(ii) ∠EFG = ∠HIJ
(iii) ∠KLH ≅ ∠RST
Try These (Text book Page No. 83)
Question 1.
If ∆ABC ≅ ∆XYZ then list the corresponding sides and corresponding angles.
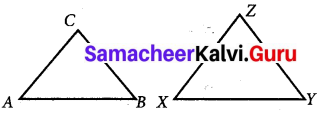
Solution:
If ∆ABC ≅ ∆XYZ
\(\overline{A B}\) ≅ \(\overline{X Y}\) – \(\overline{B C}\) ≅ \(\overline{Y Z}\)
\(\overline{A C}\) ≅ \(\overline{X Z}\)
And also
∠A ≅ ∠X – ∠B ≅ ∠Y
∠C ≅ ∠Z
![]()
Question 2.
Given triangles are congruent. Identify the corresponding parts and write the congruent statement.
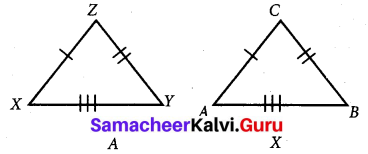
Solution:
Given the set of triangles are congruent. Also we observe from the triangles that the corresponding sides.
\(\overline{A B}\) = \(\overline{A C}\)
\(\overline{B C}\) = \(\overline{Y Z}\)
\(\overline{A C}\) = \(\overline{X Z}\)
Here three sides of ∆ABC are equal to the corresponding sides of ∆XYZ.
This criterion of congruency is side – side – side.
Question 3.
Mention the conditions needed to conclude the congruency of the triangles with reference to the above said criterions. Give reasons for your answer.
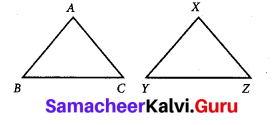
Solution:
(i) In ∆ABC and ∆XYZ
if \(\overline{A B}\) = \(\overline{X Y}\)
\(\overline{B C}\) = \(\overline{Y Z}\)
\(\overline{A C}\) = \(\overline{X Z}\)
then ∆ABC ≅ ∆XYZ. By the Side – Side -Side Congruency Criterion.

then ∆AB ≅ ∆XYZ.
By Side – Angle – Side Criterion.

then ∆ABC ≅ ∆XYZ.
By Angle – Side – Angle Congruency Critirion.

then by RHS criterion.
∆ABC ≅ ∆XYZ