Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.9

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.9

Choose the correct or the most suitable answer from the given four alternatives:

Question 1.
iⁿ + iⁿ⁺¹ + iⁿ⁺² + iⁿ⁺³ is ______
(a) 0
(b) 1
(c) -1
(d) i
Answer:
(a) 0

Question 2.
The value of \(\sum_{i=1}^{13}\left(i^{n}+i^{n-1}\right)\) is ______
(a) 1 + i
(b) i
(c) 1
(d) 0
Answer:
(a) 1 + i

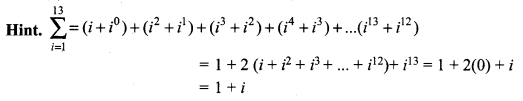
Question 3.
The area of the triangle formed by the complex numbers z, iz, and z + iz in the Argand’s diagrams is ______
(a) \(\frac { 1 }{ 2 }\) |z|
(b) |z|²
(c) \(\frac { 3 }{ 2 }\)|z|²
(d) 2|z|²
Answer:
(a) \(\frac { 1 }{ 2 }\) |z|
Hint: Area of triangle = \(\frac { 1 }{ 2 }\) bh
= \(\frac { 1 }{ 2 }\) |z| |iz|
= \(\frac { 1 }{ 2 }\) |z|²

Question 4.
The conjugate of a complex number is \(\frac{1}{i-2}\). Then, the complex number is _____
(a) \(\frac{1}{i+2}\)
(b) \(\frac{-1}{i+2}\)
(c) \(\frac{-1}{i-2}\)
(d) \(\frac{1}{i-2}\)
Answer:
(b) \(\frac{-1}{i+2}\)
Hint:

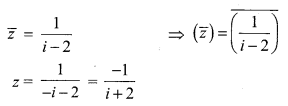
Question 5.
If \(z=\frac{(\sqrt{3}+i)^{3}(3 i+4)^{2}}{(8+6 i)^{2}}\) then |z| is equal to ______
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(c) 2
Hint:

Question 6.
If z is a non zero complex number, such that 2iz² = \(\bar{z}\) then |z| is ______
(a) \(\frac { 1 }{ 2 }\)
(b) 1
(c) 2
(d) 3
Answer:
(a) \(\frac { 1 }{ 2 }\)
Hint:

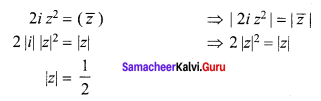
Question 7.
If |z – 2 + i| ≤ 2, then the greatest value of |z| is _______
(a) √3 – 2
(b) √3 + 2
(c) √5 – 2
(d) √5 + 2
Answer:
(d) √5 + 2
Hint:

Question 8.
If \(\left|z-\frac{3}{z}\right|\), then the least value of |z| is ______
(a) 1
(b) 2
(c) 3
(d) 5
Answer:
(a) 1
Hint:

Question 9.
If |z| = 1, then the value of \(\frac{1+z}{1+\bar{z}}\) is _______
(a) z
(b) \(\bar{z}\)
(c) \(\frac { 1 }{ z }\)
(d) 1
Answer:
(a) z
Hint:

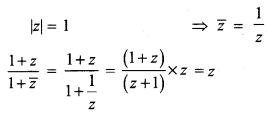
Question 10.
The solution of the equation |z| – z = 1 + 2i is _______
(a) \(\frac { 3 }{ 2 }\) – 2i
(b) –\(\frac { 3 }{ 2 }\) + 2i
(c) 2 – \(\frac { 3 }{ 2 }\)i
(d) 2 + \(\frac { 3 }{ 2 }\)i
Answer:
(a) \(\frac { 3 }{ 2 }\) – 2i

Question 11.
If |z₁| = 1, |z₂| = 2, |z₃| = 3 and |9z₁ z₂ + 4z₁ z₃ + z₂ z₃| = 12, then the value of |z₁ + z₂ + z₃| is ______
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(b) 2
Hint: |z₁ + z₂ + z₃| = 2

Question 12.
If z is a complex number such that z ∈ C/R and z + \(\frac { 1 }{ z }\) ∈ R, then |z| is ______
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(b) 1
Hint: We have

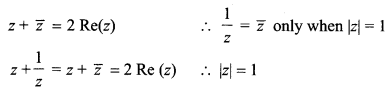
Question 13.
z₁, z₂ and z₃ are complex numbers such that z₁ + z₂ + z₃ = 0 and |z₁| = |z₂| = |z₃| = 1 then \(z_{1}^{2}+z_{2}^{2}+z_{3}^{2}\) is ______
(a) 3
(b) 2
(c) 1
(d) 0
Answer:
(d) 0
Hint:

Question 14.
If \(\frac{z-1}{z+1}\) is purely imaginary, then |z| is _______
(a) \(\frac { 1 }{ 2 }\)
(b) 1
(c) 2
(d) 3
Answer:
(b) 1

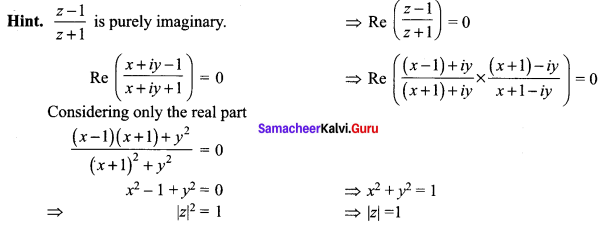
Question 15.
If z = x + iy is a complex number such that |z + 2| = |z – 2|, then the locus of z is _____
(a) real axis
(b) imaginary axis
(c) ellipse
(d) circle
Answer:
(b) imaginary axis
Hint:
|z + 2| = | z – 2|
⇒ |x + iy + 2| = |x + iy – 2|
⇒ |x + 2 + iy|² = |x – 2 + iy|²
⇒ (x + 2)² + y² = (x – 2)² + y²
⇒ x² + 4 + 4x = x² + 4 – 4x
⇒ 8x = 0
⇒ x = 0

Question 16.
The principal argument of \(\frac{3}{-1+i}\) is ______
(a) \(-\frac{5 \pi}{6}\)
(b) \(-\frac{2 \pi}{3}\)
(c) \(-\frac{3 \pi}{4}\)
(d) \(\frac{-\pi}{2}\)
Answer:
(c) \(-\frac{3 \pi}{4}\)
Hint:

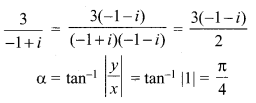
The complex number lies in III quadrant. \(\theta=-(\pi-\alpha)=-\left(\pi-\frac{\pi}{4}\right)=\frac{-3 \pi}{4}\)

Question 17.
The principal argument of (sin 40° + i cos 40°)⁵ is ______
(a) -110°
(b) -70°
(c) 70°
(d) 110°
Answer:
(a) -110°
Hint:
(sin 40° + i cos 40°)⁵
= (cos 50° + i sin 50°)⁵
= (cos 250° + i sin 250°)
250° lies in III quadrant.
To find the principal argument the rotation must be in a clockwise direction which coincides with 250°
θ = -110°

Question 18.
If (1 + i) (1 + 2i) (1 + 3i)…(1 + ni) = x + iy, then 2.5.10……(1 + n² ) is _____
(a) 1
(b) i
(c) x² + y²
(d) 1 + n²
Answer:
(c) x² + y²

Question 19.
If ω ≠ 1 is a cubic root of unity and (1 + ω)⁷ = A + B ω, then (A, B) equal to ______
(a) (1, 0)
(b) (-1, 1)
(c) (0, 1)
(d) (1, 1)
Answer:
(d) (1, 1)
Hint:

Question 20.
The principal argument of the complex number \(\frac{(1+i \sqrt{3})^{2}}{4 i(1-i \sqrt{3})}\) is _____
(a) \(\frac{2 \pi}{3}\)
(b) \(\frac{\pi}{6}\)
(c) \(\frac{5 \pi}{6}\)
(d) \(\frac{\pi}{2}\)
Answer:
(d) \(\frac{\pi}{2}\)
Hint:

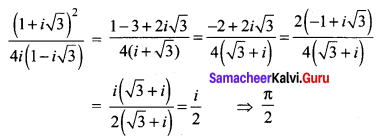
Question 21.
If α and β are the roots of x² + x + 1 = 0, then α²⁰²⁰ + β²⁰²⁰ is ______
(a) -2
(b) -1
(c) 1
(d) 2
Answer:
(b) -1
Hint:
x² + x + 1 = 0
α and β are the roots of the equation.
There are the two roots of cube roots of unity except 1.

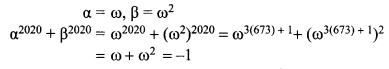
Question 22.
The product of all four values of \(\left(\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}\right)^{\frac{3}{4}}\) is ____
(a) -2
(b) -1
(c) 1
(d) 2
Answer:
(c) 1

Question 23.
If ω ≠ 1 is a cubic root of unity and \(\left|\begin{array}{cccc}{1} & {1} & {1} \\ {1} & {-\omega^{2}-1} & {\omega^{2}} \\ {1} & {\omega^{2}} & {\omega^{7}}\end{array}\right|\) = 3k, then k is equal to ______
(a) 1
(b) -1
(c) i√3
(d) -i√3
Answer:
(d) -i√3
Hint:

Question 24.
The value of \(\left(\frac{1+\sqrt{3} i}{1-\sqrt{3} i}\right)^{10}\) is ______
(a) cis \(\frac{2 \pi}{3}\)
(b) cis \(\frac{4 \pi}{3}\)
(c) -cis \(\frac{2 \pi}{3}\)
(d) -cis \(\frac{4 \pi}{3}\)
Answer:
(a) cis \(\frac{2 \pi}{3}\)
Hint:

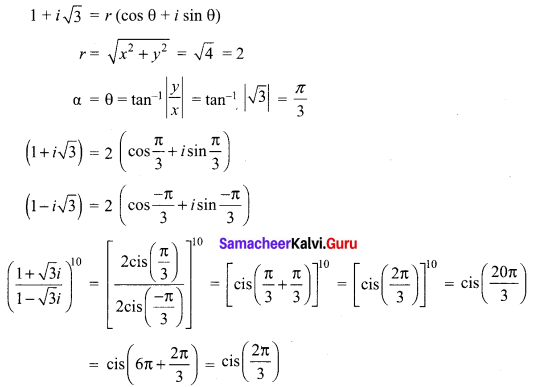
Question 25.
If ω = cis \(\frac{2 \pi}{3}\), then the number of distinct roots of \(\left|\begin{array}{ccc}{z+1} & {\omega} & {\omega^{2}} \\ {\omega} & {z+\omega^{2}} & {1} \\ {\omega^{2}} & {1} & {z+\omega}\end{array}\right|=0\) are _____
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(a) 1
Hint:

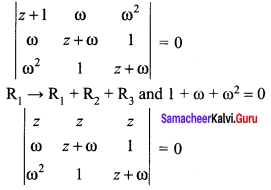
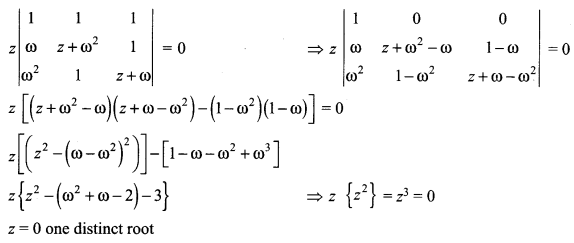
Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.9 Additional Problems

Question 1.

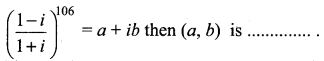
(a) (2, -1)
(b) (1, 0)
(c) (0, 1)
(d) (-1, 2)
Solution:
(b) (1, 0)

Question 2.

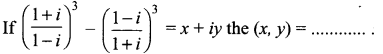
(a) (0, 2)
(b) (-2, 0)
(c) (0, -2)
(d) (-2, 0)
Solution:
(c) (0, -2)

Question 3.
The point represented by the complex number 2 – i is rotated about origin through an angle
of \(\frac{\pi}{2}\). in the clockwise direction, the new position of point is ……
(a) 1 + 2 i
(b) -1 – 2 i
(c) 2 + i
(d) -1 + 2 i
Solution:
(b) -1 – 2i
Hint.
Let z = 2 – i. Let the new position of point when the point represented by the complex number z = 2 – i is rotated about origin through an angle of \(\frac{\pi}{2}\) in the clockwise direction be denoted by z₁.

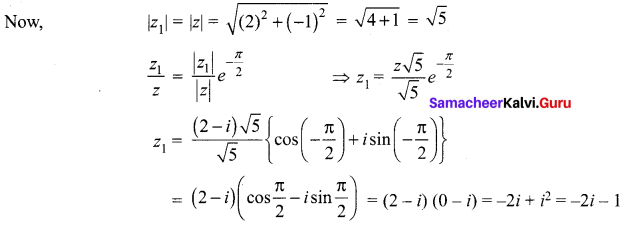
Question 4.
Fill in the blanks of the following:
For any two complex numbers z₁, z₂ and any real number a, b,
Solution:

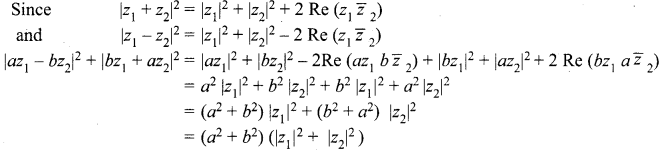
Question 5.
Multiplicative inverse of 1 + i is …..
Solution:

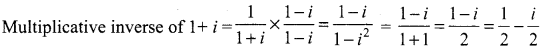
Question 6.

Solution:

Question 7.
If |z| = 4 and arg (z) = \(\frac{5 \pi}{6}\), then z = ……
Solution:

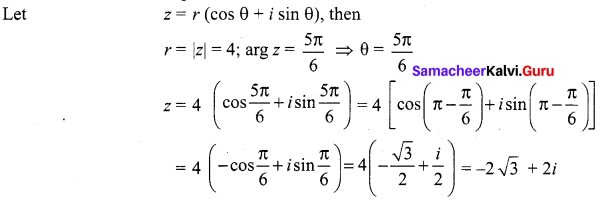
Question 8.
State true or false for the following:
(i) The order relation is defined on the set of complex numbers.
Solution:
The given statement is false because the order relation “greater than” and “less than” are not defined on the set of complex numbers.

(ii) For any complex number 2, the minimum value of |z| + |z – 1| is 1.
Solution:
Let z = x + iy be any complex number.

When x = 0, y = 0, the value of |z| + |z – 1| is minimum and the minimum value.

Hence, the given statement is true.

(iii) 2 is not a complex number.
Solution:
It is a false statement because 2 = 2 + i(0), which is of the form α + ib, and the number of the form a + ib, where a and b are real numbers is called a complex number.

(iv) The locus represented by |z – 1| = |z – i| is a line perpendicular to the join of (1, 0) and (0, 1).
Solution:
Equation of a straight line passing through (1, 0) and (0, 1) is

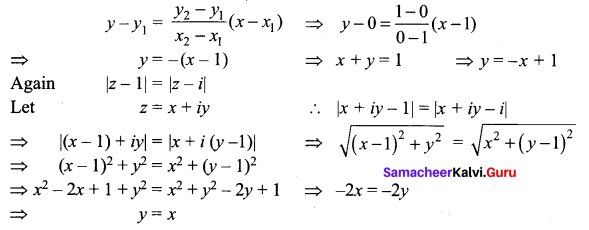
Now, the lines y = -x + 1 and y = x are perpendicular to each other, so the given statement is true.

Question 9.

Solution:
1

Question 10.
If – \(\bar{z}\) lies in the third quadrant, then z lies in the ……..
(a) first quadrant
(b) second quadrant
(c) third quadrant
(d) fourth quadrant
Solution:
(d) fourth quadrant
Hint:

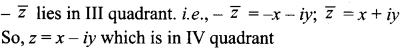
Question 11.

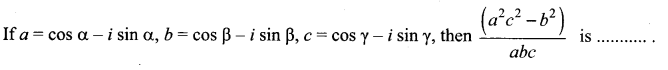
(a) cos 2(α – β + γ) + i sin 2(α – β + γ)
(b) – 2cos(α – β + γ)
(c) – 2 i sin(α – β + γ)
(d) 2 cos(α – β + γ)
Solution:
(c) -2 i sin (α – β + γ)
Hint: α β γ

Question 12.


Solution:

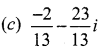
Hint:

Question 13.

(a) 1
(b) -1
(c) 0
(d)-i
Solution:
(c) 0
Hint:

Question 14.
If -i + 2 is one root of the equation ax² – bx + c = 0, then the other root is
(a) – i – 2
(b) i – 2
(c) 2 + i
(d) 2i + i
Solution:
(c) 2 + i
Hint:
Complex roots occur in pairs when -i + 2 is one root, i.e., when 2 – i is a root, the other root is 2 + i

Question 15.
The equation having 4 – 3i and 4 + 3i as roots is …….
(a) x² + 8x + 25 = 0
(b) x² + 8x – 25 = 0
(c) x² – 8x + 25 = 0
(d) x² – 8x – 25 = 0
Solution:
(c) x² – 8x + 25 = 0
Hint.

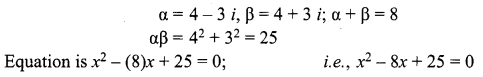
Question 16.

(a) (1, 1)
(b) (1, -1)
(c) (0, 1)
(d) (1, 0)
Solution:
(d) (1, 0)
Hint:

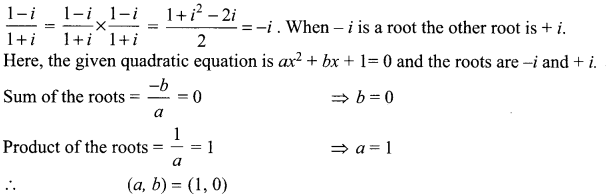
Question 17.
If – i + 3 is a root of x² – 6x + k = 0, then the value of k is

Solution:
(d) 10
Hint:
α = -i + 3 = 3 – 7 ⇒ The other root is β = 3 + i
Product of the roots = αβ = (3 – i)(3 + i) = 10
Product of the roots of x² – 6x + k = 0 is k ⇒ k = 10

Question 18.
If ω is a cube root of unity, then the value of (1 – ω + ω²)⁴ + (1 + ω – ω²)⁴ is ……
(a) 0
(b) 32
(c) -16
(d) -32
Solution:
(c) -16
Hint.

Question 19.
If ω is a cube root of unity, then the value of (1 – ω) (1 – ω²) (1 – ω⁴)(1 – ω⁸) is …….
(a) 9
(b) -9
(c) 16
(d) 32
Solution:
(a) 9
Hint.

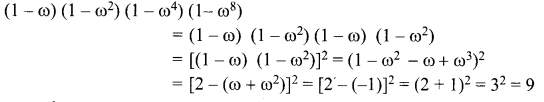
Question 20.

(a) | z | = 1
(b) | z | > 1
(c) | z | < 1
(d) None of these.
Solution:
(a) | z | = 1