Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 5 Information Processing Ex 5.3

Students can Download Maths Chapter 5 Information Processing Ex 5.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 2 Chapter 5 Information Processing Ex 5.3

Miscellaneous Practice Problems

Question 1.
Choose the correct relationship between x and y for the given table.

(i) y = x + 4
(ii) y = x + 5
(iii) y = x + 6
(iv) y = x + 7
Answer:
(iii) y = x + 6

Question 2.
Find the triangular numbers from the Pascal’s Triangle and colour them.

Solution:
Triangular numbers are numbers the objects of which can be arranged in the form of equilateral triangle.
Example : 1, 3, 6, 10, 15,…
From Pascal’s Triangle, the triangular numbers are

Question 3.
Write the first five numbers in the third slanting row of the Pascal’s Triangle and find their squares. What do you infer?
Solution:

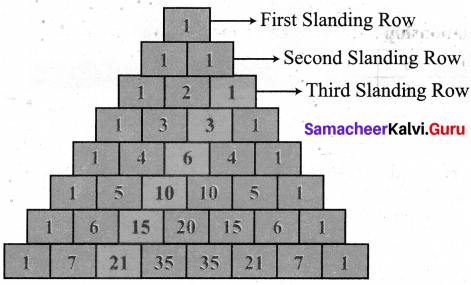
Numbers in the 3rd slanding row are 1, 3, 6, 10, 15, 21,….
The squares are 1², 3², 6², 10². 15², 21²,…. = 1, 9, 36, 100, 225, 441,…

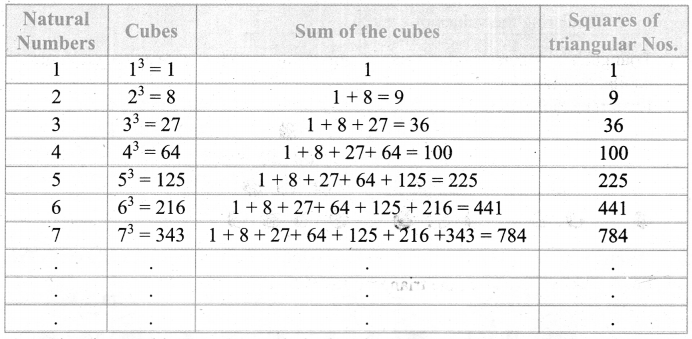
From the above table we can conclude that the squares of the triangular numbers are the sum of cubes of natural numbers.

Challenge Problems

Question 4.
Tabulate and find the relationship between the variables (x and y) for the following patterns.

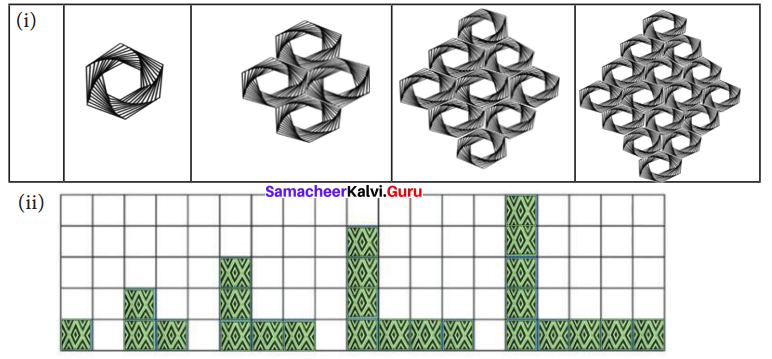
Solution:
(i) Let the number of steps be x and the number of shapes be y.
Tabulating the values of x and y

From the table
x = 1 ⇒ y = 1 = 12
x = 2 ⇒ y = 4 = 22
x = 3 ⇒ y = 9 = 32
x = 4 ⇒ y = 16 = 42
Hence the relationship between x and y is y = x2.

(ii) Let the number of steps be x and the number of shapes be y.
Tabulating the values of x and y

From the table x = 1 ⇒ y = 1 = 1
x = 2 ⇒ y = 2 + 1 = 3
x = 3 ⇒ y = 3 + 2 = 5
x = 4 ⇒ y = 4 + 3 = 7
x = 5 ⇒ y = 5 + 4 = 9
Hence the relationship between x and y is y = 2x-1.

Question 5.
Verify whether the following hexogonal shapes form a part of the Pascal’s Triangle.

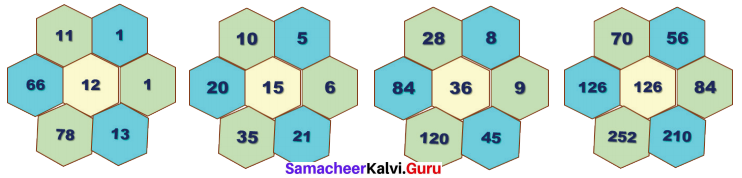
Solution:
In Pascal’s Triangle product of the 3 alternate numbers given around the hexagon is equal to the product of remaining three numbers.

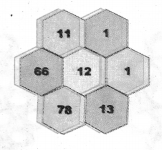
1 × 13 × 66 = 11 × 1 × 78 = 858
∴ It form a part of Pascal’s Triangle.

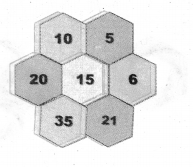
5 × 21 × 20 = 10 × 6 × 35 = 2100
∴ It form a part of Pascal’s Triangle

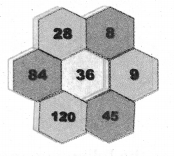
8 × 45 × 84 = 28 × 9 × 120 = 30240
∴ It form a part of Pascal’s Triangle

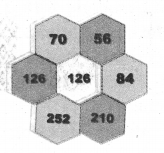
56 × 210 × 126 = 70 × 84 × 252 = 1481760
∴ It form a part of Pascal’s Triangle