Students can download 12th Business Maths Chapter 7 Probability Distributions Miscellaneous Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 7 Probability Distributions Miscellaneous Problems
Question 1.
A manufacturer of metal pistons finds that on the average, 12% of his pistons are rejected because they are either oversize or undersize. What is the probability that a batch of 10 pistons will contain
(a) no more than 2 rejects?
(b) at least 2 rejects?
Solution:
Let X be the binomial random variable denoting the number of metal pistons.
Let p be the probability of rejections.
Given that p = 12% = \(\frac{12}{100}\) = 0.12, q = 0.88, n = 10.
So X ~ B(0.12, 10). Hence the p.m.f of X is given by

Thus out of a batch of 10 pistons, the probability of no more than 2 rejects is 0.89131

Thus out of 10 pistons, the probability that at least 2 will be rejected is 0.34173
Question 2.
Hospital records show that of patients suffering from a certain disease 75% die of it. What is the probability that of 6 randomly selected patients, 4 will recover?
Solution:
Let X be the binomial random variable denoting the number of patients.
Let p be the probability that the patient will recover and q be the probability that patient will die.
According to the problem, q = 75% = 0.75 and p = 25% = 0.25 and n = 6

Hence the probability that 4 patients will recover out of 6 patients is 0.03295
![]()
Question 3.
If electricity power failures occur according to a Poisson distribution with an average of 3 failures every twenty weeks, calculate the probability that there will not be more than one failure during a particular week.
Solution:
Let X be the poisson random variable. It is given that mean λ = \(\frac{3}{20}\) = 0.15
The Poisson probability law, giving x failures per week is given by,
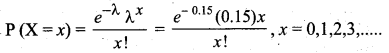
Hence probability that there will not be more than one failure is given by P (X ≤ 1)
= P(X = 0) + P(X = 1)
= e-0.15 [1 + 0.15]
= e-0.15 (1.15)
= (0.8607) (1.15)
= 0.98981
Question 4.
Vehicles pass through a junction on a busy road at an average rate of 300 per hour.
(а) Find the probability that none passes in a given minute.
(b) What is the expected number passing in two minutes?
Solution:
Let X be the Poisson random variable. It is given that mean
λ = 300/hour = 300/60 minutes = 5 per minute.
(a) The Poisson law giving x vehicles passing on a road in one minute is given by
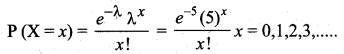
Now the probability that no vehicles pass in a given minute is given by,
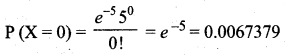
(b) E(X) = λ (i.e) No of vehicles passing per minute, since λ = 5, the expected number passing in two minutes is 10.
![]()
Question 5.
Entry to a certain University is determined by a national test. The scores on this test are normally distributed with a mean of 500 and a standard deviation of 100. Raghul wants to be admitted to this university and he knows that he must score better than at least 70% of the students who took the test. Raghul takes the test and scores 585. Will he be admitted to this university?
Solution:
Let X be the normal random variable denoting the scores of the students. Given that mean µ = 500 and s.d σ = 100. The total area under the normal curve represents the total number of students who took the test. If we multiply the values of the areas under the curve by 100, we obtain percentages.
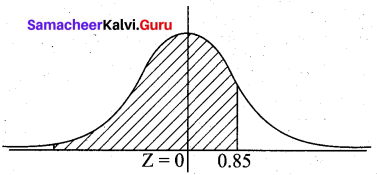
When X = 585, Z = \(\frac{585-500}{100}\) = 0.85
The proportion of students who scored below 585 is given by P[area to the left of Z = 0.85]
(i.e.) P (Z < 0.85) = 0.5 + P (0 < Z < 0.85)
= 0.5 + 0.3023 .
= 0.8023
= 80.23%
Raghul scored better than 80.23% of the students who took the test and he will be admitted to this university.
Question 6.
The time taken to assemble a car in a certain plant is a random variable having a normal distribution of 20 hours and a standard deviation of 2 hours. What is the probability that a car can be assembled at this plant in a period of time?
(a) less than 19.5 hours?
(b) between 20 and 22 hours?
Solution:
Let X be the normal random variable denoting the time taken to assemble a car.
Given that mean µ = 20 and s.d σ = 2
(a) Probability that car is assembled in less than 19.5 hours
P(X < 19.5) = P(Z < \(\frac{19.5-20}{2}\))
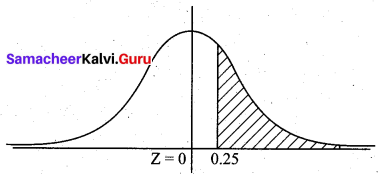
P(Z < -0.25) = P(Z > 0.25)
= 0.5 – P(0 < Z < 0.25)
= 0.5 – 0.0987
= 0.4013
(b) The probability that a car can be assembled between 20 and 22 hours is given by
P(20 < X < 22) = P(\(\frac{20-20}{2}\) < Z < \(\frac{22-20}{2}\))
P(0 < Z < 1) = 0.3413
![]()
Question 7.
The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000.
(а) What per cent of people earn less than $ 40,000?
(b) What per cent of people earn between $ 45,000 and $65,000?
(c) What per cent of people*earn more than $ 70,000?
Solution:
Let X be the normal variable denoting the annual salaries of employees.
Given the mean µ = 50,000 and s.d σ = 20,000
(a) Probability of people ehming less than $ 40,000 is given by P (X < 40,000)
= P(X < 40,000)
= P(Z < \(\frac{40000-50000}{20,000}\))
= P (Z < -0.5)
= P (0.5 < Z) (By symmetry)
= 0.5 – P(0 < Z < 0.5)
= 0.5 – 0.1915
= 0.3085
Hence people who earn less than $40,000 is 0.3085 × 100 = 30.85%
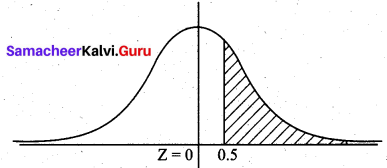
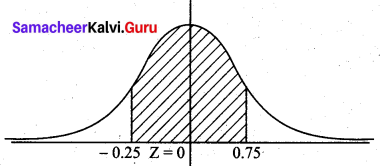
(b) Probability of people earning between $45,000 and $65,000 is P(45000 < X < 65000)
= P(\(\frac{45000-50000}{20000}\) < Z < \(\frac{65000-50000}{20000}\))
= P (-0.25 < Z < 0.75)
= P(-0.25 < Z < 0) + P (0 < Z < 0.75)
= P(0 < Z < 0.25) + P (0 < Z < 0.75)
= 0.0987 + 0.2734
= 0.3721
Hence percent of people who earn between $45,000 and $65,000 is 0.3721 × 100 = 37.21%
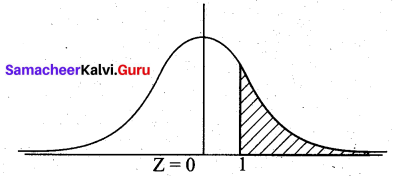
(c) Probability of people earning more than $ 70,000 is P(X > 70,000)
= P(Z > \(\frac{70000-50000}{20000}\))
= P(Z > 1)
= 0.5 – P(0 < Z < 1)
= 0.5 – 0.3413
= 0.1587
Hence percent of people who earn more than $70,000 is 0.1587 × 100 = 15.87%
Question 8.
X is a normally distributed variable with mean µ = 30 and standard deviation σ = 4. Find
(a) P(X < 40) (b) P(X > 21)
(c) P(30 < X < 35).
Solution:
Given X ~ N (µ, σ2)
µ = 30, σ = 4
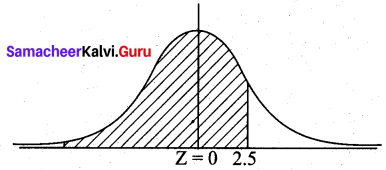
(a) P(X < 40) = P(Z < \(\frac{40-30}{4}\))
= P(Z < 2.5)
= 0.5 + P(0 < Z < 2.5)
= 0.5 + 0.4938
= 0.9938
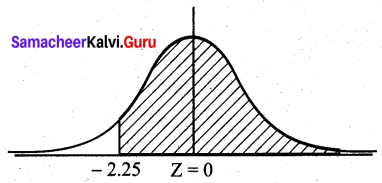
(b) P(X > 21) = P(Z > \(\frac{21-30}{4}\))
= P (Z > -2.25)
= 0.5 + P(-2.25 < Z < 0)
= 0 5 + P (0 < Z < 2.25)
= 0.5 + 0.4878
= 0.9878
(c) P(30 < X < 35)
= P(\(\frac{30-30}{4}\) < Z < \(\frac{35-30}{4}\))
= P(0 < Z < 1.25)
= 0.3944
![]()
Question 9.
The birth weight of babies is normally distributed with mean 3,500g and standard deviation 500g, What is the probability that a baby is born that weight less than 3,100g?
Solution:
Let X be the normal variable denoting the birth weights of babies. Given that the mean µ = 3500 and s.d σ = 500
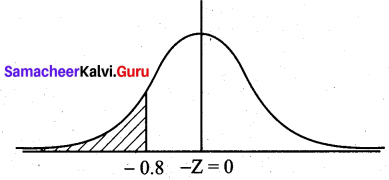
Probability that a baby is bom with weight less than 3100 g = P (X < 3100)
= P(Z < \(\frac{3100-3500}{500}\))
= P (Z < -0.8) = P (Z > 0.8) (by symmetry)
= 0.5 – P(0 < Z < 0.8)
= 0.5 – 0.2881
= 0.2119
Question 10.
People’s monthly electric bills in Chennai are normally distributed with a mean of ₹ 225 and a standard deviation of ₹ 55. Those people spend a lot of time online. In a group of 500 customers, how many would we expect to have a bill that is ₹ 100 or less?
Solution:
Let X be the normal variable denoting the monthly bills in rupees.
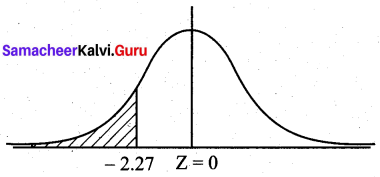
Given mean µ = 225 and s.d σ = 55
Now the probability that the bill will be ₹100 or less is P (X ≤ 100)
= P(Z ≤ \(\frac{100-225}{55}\))
= P(Z ≤ -2.27)
= 0.5 – P(-2.27 < Z < 0)
= 0.5 – P(0 < Z < 2.27)
= 0.5 – 0.4884
= 0.0116
Thus, in a group of 500 customers, we expect to have 500 × 0.0116 = 5.8 ~ 6 customers whose electric bills will be ₹ 100 or less.