Students can download 12th Business Maths Chapter 1 Applications of Matrices and Determinants Ex 1.3 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.3
Question 1.
The subscription department of a magazine sends out a letter to a large mailing list inviting subscriptions for the magazine. Some of the people receiving this letter already subscribe to the magazine while others do not. From this mailing list, 45% of those who already subscribe will subscribe again while 30% of those who do not now subscribe will subscribe. On the last letter, it was found that 40% of those receiving it ordered a subscription. What per cent of those receiving the current letter can be expected to order a subscription?
Solution:
Let X represent people who subscribe for the magazine and Y represent persons who do not subscribe for the magazine.
Now there are four cases,
(X, X) ⇒ those who already subscribed will subscribe again.
(X, Y) ⇒ those who already subscribed will not subscribe again.
(Y, X) ⇒ those who have not subscribed will do it now.
(Y, Y) ⇒ those who have not subscribed will not do it now also.
From the problem, we can see that
(X, X) = 45% = 0.45
(X, Y) = 100 – 45 = 55% = 0.55
(Y, X) = 30% = 0.3
(Y, Y) = (100 – 30) = 70% = 0.7
The transition probability matrix is given by
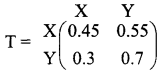
The values of X and Y are given as X = 40 % = 0.4; Y = (100 – 40 ) = 60% = 0.6
We have to predict the value of X and Y after the current letter is sent. It is done as below
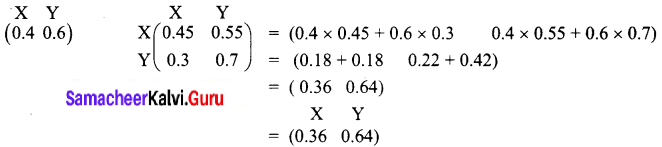
That is X = 36% and Y = 64%
Thus 36% of those receiving the current letter can be expected to order a subscription.
Question 2.
A new transit system has just gone into operation in Chennai. Of those who use the transit system this year, 30% will switch over to using the metro train next year and 70% will continue to use the transit system. Of those who use metro train this year, 70% will continue to use the metro train next year and 30% will switch over to the transit system. Suppose the population of Chennai city remains constant and that 60% of the commuters use the transit system and 40% of the commuters use metro train this year.
(i) What percent of commuters will be using the transit system after one year?
(ii) What percent of commuters will be using the transit system in the long run?
Solution:
Let T denote transit system and M denote metro train. Here again, there are four cases.
(T T) ⇒ those who use the transit system will continue to use the transit system.
(T M) ⇒ those who use the transit system will switch over to the metro train.
(M T) ⇒ those who use the metro train will change to the transit system.
(M M) ⇒ those who use the metro train will continue to use the metro train.
From the question,
(T T) =70% = 0.7.
(T M) = 30% = 0.3
(M T) = 30% = 0.3
(M M) = 70% = 0.7
The transition probability matrix is given by

The current position is given by T = 60% and M = 40%
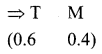
We have to predict the values of T and M after one year.
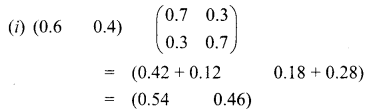
i.e, T = 0.54 = 54%
M = 0.46 = 46%
So after one year, 54% of commuters will use the transit system and 46% of commuters will use the metro train.
(ii) At equilibrium which will be reached in the long run, T + M = 1
We have,
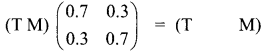
By matrix multiplications,
(0.7T + 0.3M 0.3 T + 0.7 M) = (T M)
Equating the corresponding elements,
0.7T + 0.3M = T
0.7T + 0.3 (1 – T) = T (Using T + M = 1)
0.7T + 0.3 – 0.3T = T
0.3 = 0.6T
T = 0.5
T = 50%
Thus, in the long run, 50% of the commuters will be using transit system and 50% will be using the metro train.
Question 3.
Two types of soaps A and B are in the market. Their present market shares are 15% for A and 85% for B. Of those who bought A the previous year, 65% continue to buy it again while 35% switch over to B. Of those who bought B the previous year, 55% buy it again and 45% switch over to A. Find their market shares after one year and when is the equilibrium reached?
Solution:
A and B are the two types of soaps. The current market shares are 15% and 85%.
This is represented as
(A B)
(0.15 0.85)
(A A) ⇒ those who bought A previous year will again buy A = 65 % = 0.65
(A B) ⇒ those who bought A previous year will buy soap B now = 35 % = 0.35
(B A) ⇒ those who bought B previous year will buy A now = 45 % = 0.45
(B B) ⇒ those who bought B previous year will buy it again = 55 % = 0.55
The transition probability matrix is
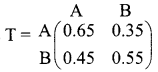
(i) Their market shares after one year is given by

So after one-year market shares of soap A will be 48% and soap B will be 52%
(ii) At equilibrium, A + B = 1
We have
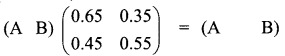
By matrix multiplication,
(0.65A + 0.45B 0.35A + 0.55B) = (A B)
Equating the corresponding elements,
0.65 A + 0.45 B = A
0.65 A + 0.45 A(1 – A) = A (Using A + B = 1)
0.65 A + 0.45 – 0.45 A = A
0.45 = 0.8 A
A = 0.5625 (or) A = 56.25 %
B = 100 – 56.25 = 43.75%
The equilibrium is reached when the market share of soap A is 56.25% and the market share of soap B is 43.75%
Question 4.
Two products A and B currently share the market with shares 50% and 50% each respectively. Each week some brand switching takes place. Of those who bought A the previous week, 60% buy it again whereas 40% switch over to B. Of those who bought B the previous week, 80% buy it again whereas 20% switch over to A. Find their shares after one week and after two weeks. If the price war continues, when is the equilibrium reached?
Solution:
Given that two products A and B have shared 50 % and 50% respectively.
(A A) ⇒ those who bought A the previous week will buy it again = 60 % = 0.6
(A B) ⇒ those who bought A the previous week will buy B now = 40 % = 0.4
(B A) ⇒ those who bought B the previous week will switch to A = 20 % = 0.2
(B B) ⇒ those who bought B will again buy B = 80 % = 0.8
The transition probability matrix is given by
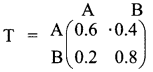
The current position of A and B in the market is
![]()
After one week
The shares of A and B are given by
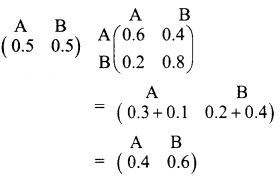
So after one week the market share of A is \(\frac{0.4}{100}\) × 100 = 40% and that of B is \(\frac{0.6}{100}\) × 100 = 60%
After two weeks
The shares of A and B are given by
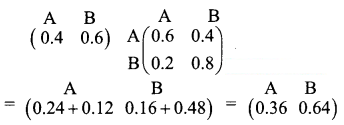
Thus after two weeks, A will have 36% of shares, and B will have 64% of shares.
As time goes, equilibrium will be reached in the long run.
At this point A + B = 1
We have

By matrix multiplication,
(0.6A + 0.2B 0.4A + 0.8B) = (A B)
Equating the corresponding elements,
0.6A + 0.2B = A
0.6A + 0.2(1 – A) = A (using A + B = 1)
0.6A + 0.2 – 0.2A = A
0.2 = A – 0.4A
A = \(\frac{0.2}{0.6}\) = 0.33 = 33%
B = 1 – 0.33 = 0.67 = 67%
Thus the equilibrium is reached when the share of A is 33% and share of B is 67%.