Students can Download Physics Chapter 9 Kinetic Theory of Gases Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Physics Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 9 Kinetic Theory of Gases
Samacheer Kalvi 11th Physics Kinetic theory of Gases Textual Evaluation Solved
Samacheer Kalvi 11th Physics Kinetic Theory of Gases Multiple Choice Questions
Question 1.
A particle of mass m is moving with speed u in a direction which makes 60° with respect to x axis. It undergoes elastic collision with the wall. What is the change in momentum in x and y direction?
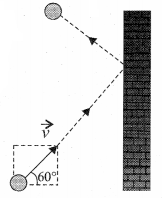
Answer:
\(\Delta p_{x}=-2 m u, \Delta p_{y}=0\)
Solution:
The change in momentum of the molecule in x direction
\(\Delta p_{x}\) = Final momentum – Initial momentum ,
= After collision – Before collision
= – mu – mu = – 2mu
The change in momentum of the molecule in Y direction \(\Delta p_{y}\) = 0
Question 2.
A sample of ideal gas is at equilibrium. Which of the following quantity is zero?
(a) rms speed
(b) average speed
(c) average velocity
(d) most probable speed
Answer:
(c) average velocity
![]()
Question 3.
An ideal gas is maintained at constant pressure. If the temperature of an ideal gas increases
from 100K to 1000K then the rms speed of the gas molecules
(a) increases by 5 times
(b) increases by \(\sqrt{10}\) times
(c) remains same
(d) increases by 7 times
Answer:
(b) increases by \(\sqrt{10}\) times
Solution:

Question 4.
Two identically sized rooms A and B are.connected by an open door. If the room A is air conditioned such that its temperature is 4° lesser than room B, which room has more air in it?
(a) Room A
(b) RoomB
(c) Both room has same air
(d) Cannot be determined
Answer:
(a) Room A
Question 5.
The average translational kinetic energy of gas molecules depends on ……
(a) number of moles and T
(b) only on T
(c) P and T
(d) P only
Answer:
(a) number of moles and T
![]()
Question 6.
If the internal energy of an ideal gas U and volume V are doubled then the pressure ……
(a) doubles
(b) remains same
(c) halves
(d) quadruples
Answer:
(b) remains same
Solution:

Question 7.
The ratio \(\gamma=\frac{\mathrm{C}_{\mathrm{p}}}{\mathrm{C}_{\mathrm{v}}}\) for a gas mixture consisting of 8 g of helium and 16 g of oxygen is …… [Physics Olympiad – 2005]
(a) 23/15
(b) 15/23
(c) 27/17
(d) 17/27
Answer:
(c) 27/17
Solution:

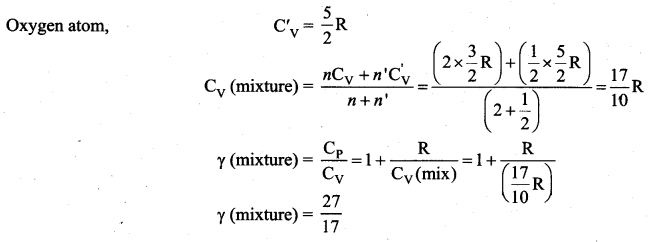
Question 8.
A container has one mole of monoatomic ideal gas. Each molecule has /degrees of freedom.
What is the ratio of \(\gamma=\frac{\mathbf{C}_{\mathbf{P}}}{\mathbf{C}_{\mathbf{V}}}\) = ?

Answer:
(d) \(\frac{f+2}{f}\)
Solution:

Question 9.
If the temperature and pressure of a gas is doubled the mean free path of the gas molecules
(a) remains same
(b) doubled
(c) tripled
(d) quadruples
Answer:
(a) remains same
Solution:
Mean free path of the molecule
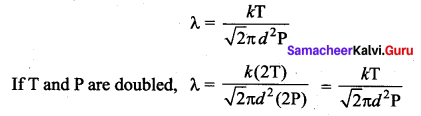
Question 10.
Which of the following shows the correct relationship between the pressure and density of an ideal gas at constant temperature?
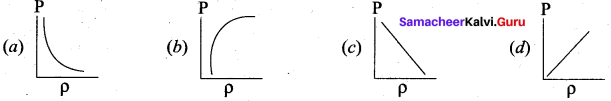
Answer:
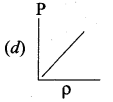
Question 11.
A sample of gas consists of µ1 moles of monoatomic molecules, µ2 moles of diatomic molecules and µ3 moles of linear triatomic molecules. The gas is kept at high temperature. What is the total number of degrees of freedom?
(a) [3µ1 + 7(µ2 + µ3)] NA
(b) [3µ1 + 7µ2 + 6µ3] NA
(c) [7µ1 + 3(µ2 + µ3)] NA
(d) [3µ1 + 6(µ2 + µ3)] NA
Answer:
(a) [3µ1 + 7(µ2 + µ3)] NA
![]()
Question 12.
If SP and SV denote the specific heats of nitrogen gas per unit mass at constant pressure and constant volume respectively, then …….. [JEE 2007]
(a) SP – SV = 28 R
(b) SP – SV = R/28
(c) SP – SV = R/14
(d) SP – SV = R
Answer:
(b) SP – SV = R/28
Question 13.
Which of the following gases will have least rms speed at a given temperature?
(a) Hydrogen
(b) Nitrogen
(c) Oxygen
(d) Carbon dioxide
Answer:
(d) Carbon dioxide
Question 14.
For a given gas molecule at a fixed temperature, the area under the Maxwell-Boltzmann distribution curve is equal to
![]()
Answer:
(a) \(\frac{\mathrm{PV}}{k T}\)
Question 15.
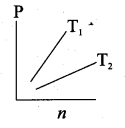
The following graph represents the pressure versus number density for ideal gas at two different temperatures T1 and T2. The graph implies …….
(a) T1 = T2
(b) T1 > T2
(c) T1 < T2
(d) Cannot be determined
Answer:
(b) T1 > T2
Samacheer Kalvi 11th Physics Kinetic Theory of Gases Short Answer Questions
Question 1.
What is the microscopic origin of pressure?
Answer:
According to the kinetic theory of a gases, the pressure exerted by the molecules depends on
(i) Number density n = \(\frac{N}{V}\)
(ii) Mass of the molecule
(iii) Mean square speed
![]()
![]()
Question 2.
What is the microscopic origin of temperature?
Answer:
The average K.E per molecule \(\overline{\mathrm{KE}}=\epsilon=\frac{3}{2} k \mathrm{T}\)
The equation implies that the temperature of a gas is a measure of the average translational K.E. per molecule of the gas.
Question 3.
Why moon has no atmosphere?
Answer:
Moon has no atmosphere. The escape speed of gases on the surface of Moon is much less than the root mean square speeds of gases due to low gravity. Due to this all the gases escape from the surface of the Moon.
Question 4.
Write the expression for rms speed, average speed and most probable speed of a gas
molecule.
Answer:

Question 5.
What is the relation between the average kinetic energy and pressure?
Answer:
The internal energy of the gas U = \(\frac{3}{2} \mathrm{N} k \mathrm{T}\)
The above equation can also be written as U = \(\frac{3}{2} \mathrm{PV}\)
since PV = NkT
![]()
From the equation (1), we can state that the pressure of the gas is equal to two thirds of internal energy per unit volume or internal energy density \(\left(u=\frac{U}{V}\right)\)
Writing pressure in terms of mean kinetic energy density

where ρ = nm = mass density (Note n is number density)
Multiply and divide R.H. S of equation (2) by 2, we get

From the equation (3), pressure is equal to \(\frac{2}{3}\) of mean kinetic energy per unit volume.
![]()
Question 6.
Define the term degrees of freedom.
Answer:
The minimum number of independent coordinates needed to specify the position and configuration of a thermo-dynamical system in space is called the degree of freedom of the system.
Question 7.
State the law of equipartition of energy.
Answer:
According to kinetic theory, the average kinetic energy of system of molecules in thermal equilibrium at temperature T is uniformly distributed to all degrees of freedom (x or y or z
directions of motion) so that each degree of freedom will get \(\frac{1}{2}\) kT of energy. This is called law of equipartition of energy.
Question 8.
Define mean free path and write down its expression.
Answer:
The average distance travelled by the molecule bfetween collisions is called mean free path (λ).

Question 9.
Deduce Chailes’ law based on kinetic theory.
Answer:
Charles’ law: From PV = \(\frac{2}{3} U\). For a fixed pressure, the volume of the gas is proportional to internal energy of the gas or average kinetic energy of the gas and the average kinetic energy is directly proportional to absolute temperature. It implies that
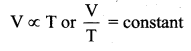
This is Charles’ law.
![]()
Question 10.
Deduce Boyle’s law based on kinetic theory.
Answer:
Boyle’s law: From PV = \(\frac{2}{3} U\)
But the internal energy of an ideal gas is equal to N times the average kinetic energy (ε) of each molecule. U = Nε. For a fixed temperature, the average translational kinetic energy ε will remain constant. It implies that
![]()
Thus PV = constant Therefore, pressure of a given gas is inversely proportional to its volume provided the temperature remains constant. This is Boyle’s law.
Question 11.
Deduce Avogadro’s law based on kinetic theory.
Answer:
Avogadro’s law: This law states that at constant temperature and pressure, equal volumes of all gases contain the same number of molecules. For two different gases at the same temperature and pressure, according to kinetic theory of gases,
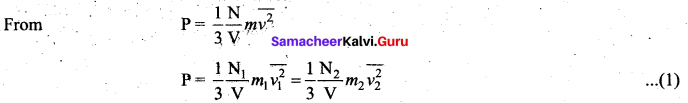
At the same temperature, average kinetic energy per molecule is the same for two gases.

Dividing the equation (1) by (2) we get N1 = N2
This is Avogadro’s law. It is sometimes referred to as Avogadro’s hypothesis or Avogadro’s Principle.
Question 12.
List the factors affecting the mean free path.
Answer:
- Mean free path increases with increasing temperature. As the temperature increases, the average speed of each molecule will increase. It is the reason why the smell of hot sizzling food reaches several metre away than smell of cold food.
- Mean free path increases with decreasing pressure of the gas and diameter of the gas molecules.
![]()
Question 13.
What is the reason for Brownian motion?
Answer:
According to kinetic theory, any particle suspended in a liquid or gas is continuously bombarded from all the directions so that the mean free path is almost negligible. This leads to the motion of the particles in a random and zig-zag manner.
Samacheer Kalvi 11th Physics Kinetic Theory of Gases Long Answer Questions
Question 1.
Write down the postulates of kinetic theory of gases.
Answer:
- All the molecules of a gas are identical, elastic spheres.
- The molecules of different gases are different.
- The number of molecules in a gas is very large and the average separation between them is larger than size of the gas molecules.
- The molecules of a gas are in a state of continuous random motion.
- The molecules collide with one another and also with the walls of the container.
- These collisions are perfectly elastic so that there is no loss of kinetic energy during collisions.
- Between two successive collisions, a molecule moves with uniform velocity.
- The molecules do not exert any force of attraction or repulsion on each other except during collision. The molecules do not possess any potential energy and the energy is wholly kinetic.
- The collisions are instantaneous. The time spent by a molecule in each collision is very small compared to the time elapsed between two consecutive collisions.
- These molecules obey Newton’s laws of motion even though they move randomly.
Question 2.
Derive the expression of pressure exerted by the gas on the walls of the container.
Answer:
Expression for pressure exerted by a gas: Consider a monoatomic gas of N molecules each having a mass m inside a cubical container of side l.
The molecules of the gas are in random motion. They collide with each other and also with the walls of the container. As the collisions are elastic in nature, there is no loss of energy, but a change in momentum occurs.
The molecules of the gas exert pressure on the walls of the container due to collision on it. During each collision, the molecules impart certain momentum to the wall. Due to transfer of momentum, the walls experience a continuous force. The force experienced per unit area of the walls of the container determines the pressure exerted by the gas. It is essential to determine the total momentum transferred by the molecules in a short interval of time.
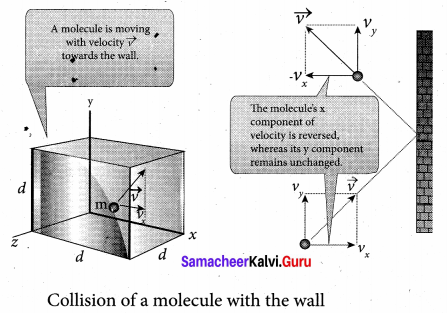
A molecule of mass m moving with a velocity \(\vec{v}\) having components (vx, vy, vz) hits the right side wall. Since we have assumed that the collision is elastic, the particle rebounds with same speed and its x-component is reversed. This is shown in the figure. The components of velocity of the molecule after collision are (- vx, vy, vz).
The x-component of momentum of the molecule before collision = mvx
The x-component of momentum of the molecule after collision = – mvx
The change in momentum of the molecule in x direction = Final momentum – initial momentum = – mvx – mvx = – 2mvx
According to law of conservation of linear momentum, the change in momentum of the wall = 2mvx
The number of molecules hitting the right side wall in a small interval of time At.
The molecules within the distance of vx∆t from the right side wall and moving towards’ the right will hit the wall in the time interval ∆t. The number of molecules that will hit the right side wall in a time interval At is equal to the product of volume (Avx∆t) and number density of the molecules (n). Here A is area of the wall and n is number of molecules per unit volume \(\frac{\mathrm{N}}{\mathrm{V}}\).
We have assumed that the number density is the same throughout the cube.
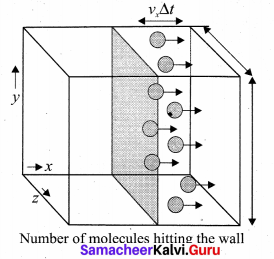
Not all the n molecules will move to the right, therefore on an average only half of the n molecules move to the right and the other half moves towards left side.
The number of molecules that hit the right side wall in a time interval ∆t
![]()
In the same interval of time At, the total momentum transferred by the molecules
![]()
From Newton’s second law, the change in momentum in a small interval of time gives rise to force.
The force exerted by the molecules on the wall (in magnitude)
![]()
Pressure, P = force divided by the area of the wall

Since all the molecules are moving completely in random manner, they do not have same speed. So we can replace the term \(v_{x}^{2}\) by the average \(\overline{v_{x}^{2}}\) in equation (4).
![]()
Since the gas is assumed to move in random direction, it has no preferred direction of motion (the effect of gravity on the molecules is neglected). It implies that the molecule has same average speed in all the three direction. So, \(\overline{v_{x}^{2}}=\overline{v_{y}^{2}}=\overline{v_{z}^{2}}\) . The mean square speed is written as

Question 3.
Explain in detail the kinetic interpretation of temperature.
Answer:
To understand the microscopic origin Of temperature in the same way, from pressure exerted by a gas,

Comparing the equation (1) with ideal gas equation PV = NkT,
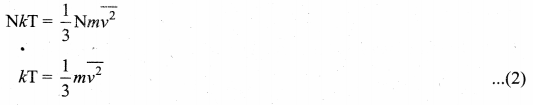
Multiply the above equation by \(\frac{3}{2}\) on both sides,
![]()
R.H.S. of the equation (3) is called average kinetic energy of a single molecule (\(\overline{\mathrm{KE}}\)).
The average kinetic energy per molecule
![]()
Equation (3) implies that the temperature, of a gas is a measure of the average translatiohal kinetic energy per molecule of the gas.
Equation (4) is a very important result from kinetic theory of gas. We can infer the following from this equation.
(i) The average kinetic energy of the molecule is directly proportional to absolute temperature of the gas. The equation (3) gives the connection between the macroscopic world (temperature) to microscopic world (motion of molecules).
(ii) The average kinetic energy of each molecule depends only on temperature of the gas hot on mass of the molecule. In other words, if the temperature of an ideal gas is measured using thermometer, the average kinetic energy of each molecule can be calculated without seeing the molecule through naked eye.
By multiplying the total number of gas molecules with average kinetic energy of each molecule, the internal energy of the gas is obtained.

Here, we understand that the internal energy of an ideal gas depends only on absolute temperature and is independent of pressure and volume.
![]()
Question 4.
Describe the total degrees of freedom for monoatomie molecule, diatomic molecule and triatomic molecule,
Monoatomie molecule: A monoatomie molecule by virtue of its nature has only three translational degrees of freedom.
Therefore f = 3
Example: Helium, Neon, Argon
Diatomic molecule: There are two cases.
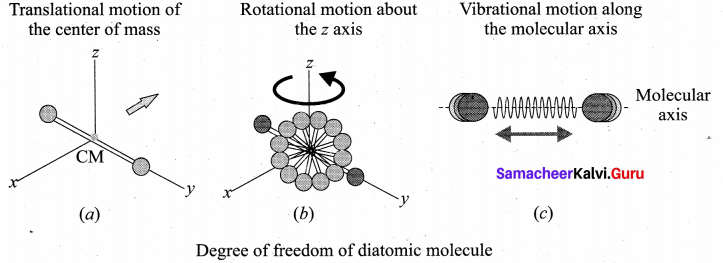
(i) At Normal temperature: A molecule of a diatomic gas consists of two atoms bound to each other by a force of attraction. Physically the molecule can be regarded as a system of two point masses fixed at the ends of a massless elastic spring. The center of mass lies in the center of the diatomic molecule. So, the motion of the center of mass requires three translational degrees of freedom (figure a). In addition, the diatomic molecule can rotate about three mutually perpendicular axes (figure b). But the moment of inertia about its own axis of rotation is negligible. Therefore, it has only two rotational degrees of freedom (one rotation is about Z axis and another rotation is about Y axis). Therefore totally there are five degrees of freedom.
f = 5
2. At High Temperature: At a very high temperature such as 5000 K, the diatomic molecules possess additional two degrees of freedom due to vibrational motion [one due to kinetic energy of vibration and the other is due to potential energy] (figure c ). So totally there are seven degrees of freedom.
f = 7
Examples: Hydrogen, Nitrogen, Oxygen.
Triatomic molecules: There are two cases.
Linear triatomic molecule:
In this type, two atoms lie on either side of the central atom. Linear triatomic molecule has three translational degrees of freedom. It has two rotational degrees of freedom because it is similar to diatomic molecule except there is an additional atom at the center. At normal temperature, linear triatomic molecule will have five degrees of freedom. At high temperature it has two additional vibrational degrees of freedom. So a linear triatomic molecule has seven degrees of freedom.
Example: Carbon dioxide.
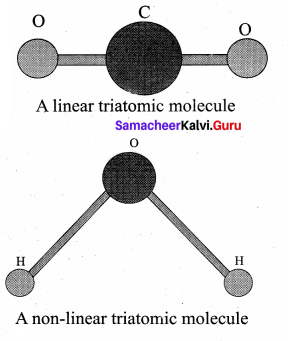
Non-linear triatomic molecule: In this case, the three atoms lie at the vertices of a triangle.
It has three translational degrees of freedom and three rotational degrees of freedom about three mutually orthogonal axes. The total degrees of freedom.
f = 6
Example: Water, Sulphurdioxide.
Question 5.
Derive the ratio of two specific heat capacities of monoatomic, diatomic and triatomic molecules.
Answer:
Application of law of equipartition energy in specific heat of a gas, Meyer’s relation CP – CV = R connects the two specific heats for one mole of an ideal gas.
Equipartition law of energy is used to calculate the value of CP – CV and the ratio between them \(\gamma=\frac{\mathrm{C}_{\mathrm{P}}}{\mathrm{C}_{\mathrm{V}}}\). Here γ is called adiabatic exponent.


Note that the CV and CP are higher for diatomic molecules than the mono atomic molecules. It implies that to increase the temperature of diatomic gas molecules by 1°C it require more heat energy than monoatomic molecules.
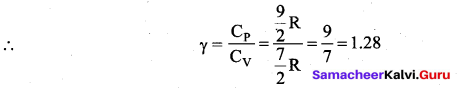
(iii) Triatomic molecule
(a) Linear molecule:

(b) Non-linear molecule:
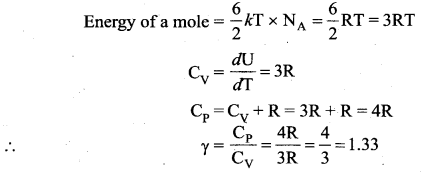
Note that according to kinetic theory model of gases the specific heat capacity at constant volume and constant pressure are independent of temperature. But in reality it is not sure.
The specific heat capacity varies with the temperature.
![]()
Question 6.
Explain in detail the Maxwell Boltzmann distribution function.
Answer:
Maxwell-Boltzmann: In speed distribution function
Consider an atmosphere, the air molecules are moving in random directions. The speed of each molecule is not the same even though macroscopic parameters like temperature and pressure are fixed. Each molecule collides with every other molecule and they exchange their speed. In the previously we calculated the rms speed of each molecule and not the speed of each molecule which is rather difficult. In this scenario we can find the number of gas molecules that move with the speed of 5 ms-1 to 10 ms-1 or 10 ms-1 to 15 ms-1 etc. In general our interest is to find how many gas molecules have the range of speed from v to v + dv. This is given by Maxwell’s speed distribution function.
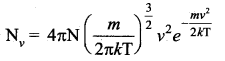
The above expression is graphically shown as follows:
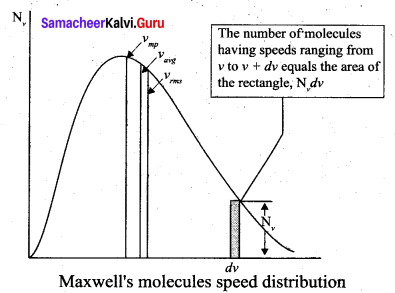
From the above figure, it is clear that, for a given temperature the number of molecules having lower speed increases parabolically but decreases exponentially after reaching most probable speed. The ms speed, average speed and most probable speed are indicated in the figure. It can be seen that the rms speed is greatest among the three.
(i) The area under the graph will give the total number of gas molecules in the system
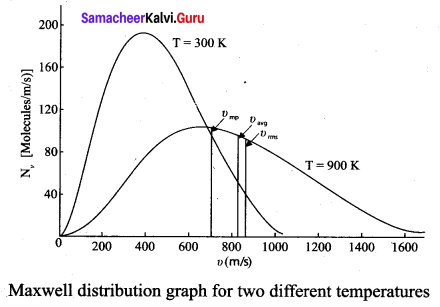
(ii) Figure 2 shows the speed distribution graph for two different temperatures. As temperature increases, the peak of the curve is shifted to the right. It implies that the average speed of each molecule will increase. But the area under each graph is same since it represents the total number of gas molecules.
Question 7.
Derive the expression for mean free path of the gas.
Answer:
Expression for mean free path
We know from postulates of kinetic theory that the molecules of a gas are in random motion and they collide with each other. Between two successive collisions, a molecule moves along a straight path with uniform velocity. This path is called mean free path. Consider a system of molecules each with diameter d. Let n be the number of molecules per unit volume. Assume that only one molecule is in motion and all others are at rest.
If a molecule moves with average speed v in a time t, the distance travelled is vt. In this time t, consider the molecule to move in an imaginary cylinder of volume πd2vt. It collides with any molecule whose center is within this cylinder. Therefore, the number of collisions is equal to the number of molecules in the volume of the imaginary cylinder. It is equal to πd2vtn. The total path length divided by the number of collisions in time t is the mean free path.

Though we have assumed that only one molecule is moving at a time and other molecules are at rest, in actual practice all the molecules are in random motion. So the average relative speed of one molecule with respect to other molecules has to be taken into account. After some detailed calculations the correct expression for mean free path
![]()
The equation (2) implies that the mean free path is inversely proportional to number density. When the number density increases the molecular collisions increases so it decreases the distance travelled by the molecule before collisions.
Case 1: Rearranging the equation (2) using ‘m’ (mass of the molecule)
![]()
But mn = mass per unit volume = ρ (density of the gas)

The equation (4) implies the following:
(i) Mean free path increases with increasing temperature. As the temperature increases, the average speed of each molecule will increase. It is the reason why the smell of hot sizzling food reaches several meter away than smell of cold food.
(ii) Mean free path increases with decreasing pressure of the gas and diameter of the gas molecules.
Question 8.
Describe the Brownian motion.
Answer:
Brownian motion is due to the bombardment of Brownian motion suspended particles by molecules of the surrounding fluid. But during 19th century people did not accept that every matter is made up of small atoms or molecules. In the year 1905, Einstein gave systematic theory of Brownian motion based on kinetic theory and he deduced the average size of molecules.
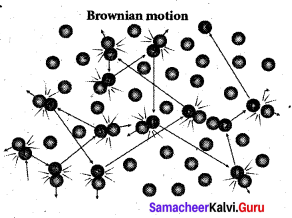
According to kinetic theory, any particle suspended – in a liquid or gas is continuously bombarded from all the directions so that the mean free path is almost negligible. This leads to the motion of the particles in a random and zig-zag manner. But when we put our hand in water it causes no random motion because the mass of our hand is so large that the momentum transferred by the molecular collision is not enough to move our hand.
Factors affecting Brownian Motion:
- Brownian motion increases with increasing temperature.
- Brownian motion decreases with bigger particle size, high viscosity and density of the liquid (or) gas.
Samacheer Kalvi 11th Physics Kinetic Theory of Gases Numerical Problems
Question 1.
A fresh air is composed of nitrogen N2 (78%) and oxygen O2 (21%). Find the rms speed of N2 and O2 at 20°C.
Answer:
Absolute temperature T = 20°C + 273 = 293K
Gas constant R = 8.32 J mol-1 K-1

![]()
Question 2.
If the rms speed of methane gas in the Jupiter’s atmosphere is 471.8 m s-1, show that the surface temperature of Jupiter is sub-zero.
Answer:
RMS speed of methane gas (vrms) = 471.8 ms-1
Molar mass of methane gas (M) = 16.04 g per mol

Question 3.
Calculate the temperature at which the rms velocity of a gas triples its value at S.T.P. (Standard temperature T1 = 273 K)
Answer:
At STP temperature T1 = 273 K

Question 4.
A gas is at temperature 80°C and pressure \(5 \times 10^{-10} \mathrm{N} \mathrm{m}^{-2}\). What is the number of molecules per m3 if Boltzmann’s constant is \(1.38 \times 10^{-23} \mathrm{J} \mathrm{K}^{-1}\).
Answer:

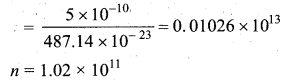
Question 5.
From kinetic theory of gases, show that Moon cannot have an atmosphere (Assume k = 1.38 × 10-23 J K-1 Temperature T = 0°C = 273 K).
Answer:

![]()
Question 6.
If 1020 oxygen molecules per second strike 4 cm2 of wall at an angle of 30° with the normal when moving at a speed of 2 × 103 ms-1, find the pressure exerted on the wall.
(mass of 1 atom = 2.67 × 10-26 kg).
Answer:
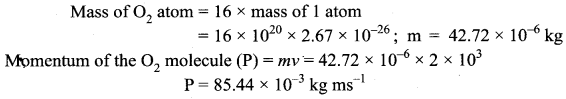
Momentum normal to the wall at angle 30°

Question 7.
During an adiabatic process, the pressure of a mixture of monoatomic and diatomic gases is found to be proportional to the cube of the temperature. Find the value of ![]()
Answer:

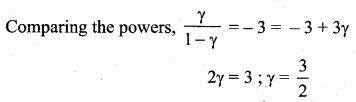
Question 8.
Calculate the mean free path of air molecules at STP. The diameter of N2 and O2 is about 3 × 10-10 m.
Answer:

Question 9.
A gas made of a mixture of 2 moles of oxygen and 4 moles of argon at temperature T. Calculate the energy of the gas in terms of RT. Neglect the vibrational modes.
Answer:
For two moles of diatomic nitrogen with no vibrational mode,
![]()
For four mole of monatomic argon,
![]()
Total energy of the gas, U = U1 + U2 = 5 RT + 6 RT
U = 11 RT
Question 10.
Estimate the total number of air molecules in a room of capacity 25 m3 at a temperature of 27°C.
Answer:
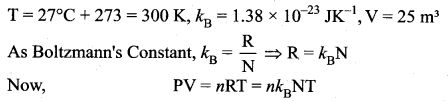
The number of molecules in the room,
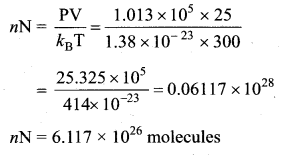
Samacheer Kalvi 11th Physics Kinetic Theory of Gases Additional Multiple Choice Questions
I. Choose the correct answer from the following:
Question 1.
Oxygen and hydrogen gases are at the same temperature the ratio of the average K.E of an oxygen molecule and that of a hydrogen molecule is
(a) 16
(b) 4
(c) 1
(d) \(\frac{1}{4}\)
Answer:
(c) 1
Solution:
P1V1 = P2V2, if T is constant.
![]()
Question 2.
According to the kinetic theory of gases,
(a) the pressure of a gas is proportional to the rms speed of the molecules.
(b) the rms speed of the molecules of a gas is proportional to the absolute temperature.
(c) the rms speed of the molecules of a gas is proportional to the square root of the absolute temperature.
(d) the pressure of a gas is proportional to the square root of the rms speed of the molecules.
Answer:
(c) the rms speed of the molecules of a gas is proportional to the square root of the absolute temperature.
Solution:
The rms speed of the molecules of a gas is proportional to the square root of the absolute temperature. .
Question 3.
Pressure exerted by a perfect gas is equal to
(a) mean K.E. per unit volume.
(b) half of mean K.E. per unit volume.
(c) one-third of mean K.E. per unit volume.
(d) two-third of mean K.E. per unit volume.
Answer:
(d) two-third of mean K.E. per unit volume.
Solution: P = \(\frac{2}{3}\) K.E. (average K.E. of the gas per unit volume).
Question 4.
The temperature of an ideal gas is increased from 27°C to 927°C. The root mean square speed of its molecules becomes.
(a) 3 times
(b) double
(c) 4 times
(d) 6 times
Answer:
(b) double
1200
Solution:
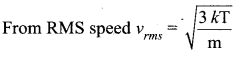
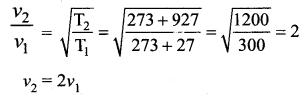
![]()
Question 5.
Two gases are enclosed in a container at constant temperature. One of the gases, which is diatomic, has relative molecular mass eight times the other, which is monoatomic. The ratio pf the rms speed of the molecules of the monoatomic gas to that of the molecules of the diatomic gas is
(a) 8
(b) 4
(c) 2\(\sqrt{2}\)
(d) 2
Answer:
(c) 2\(\sqrt{2}\)
Solution:
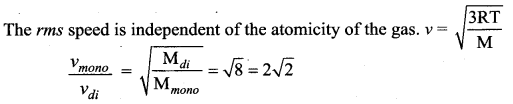
Question 6.
If the absolute temperature of a gas is increased 3 times the rms velocity of the molecules will be ………
(a) 3 times
(b) 9 times
(c) 73 times
(d) 76 times
Answer:
(c) 73 times
Question 7.
At a given temperature which of the following gases possesses maximum rms velocity of molecules?
(a) H2
(b) O2
(c) N2
(d) CO2
Answer:
(a) H2
Solution:
![]()
Question 8.
Two vessels have equal volumes. One of them contains hydrogen at one atmosphere and the other helium at two atmospheres. If both the samples are at the same temperature, the rms velocity of the hydrogen molecules is …..
(a) equal to that of the helium molecules
(b) twice that of the helium molecules
(c) half that of the helium molecules
(d) \(\sqrt{2}\) times that of the helium molecules
Answer:
(d) \(\sqrt{2}\) times that of the helium molecules
Solution:
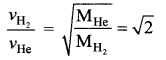
Question 9.
A gas is enclosed in a container which is then placed on a fast moving train. The temperature of the gas …..
(a) rises
(b) remains unchanged
(c) falls
(d) becomes unsteady
Answer:
(c) falls
Question 10.
The mean translational K.E. of a perfect gas molecule at absolute temperature T is (K is Boltzmann constant)

Answer:
(c) \(\frac{3}{2} k \mathrm{T}\)
![]()
Question 11.
Ajar has mixture of hydrogen and Oxygen gases in the ratio 1 : 5. The ratio of mean kinetic energies of hydrogen and Oxygen molecules is ……..
(a) 1 : 5
(b) 5 : 1
(c) 1 : 1
(d) 1 : 25
Answer:
(c) 1 : 1
Solution:
The mean kinetic energy depends only on the temperature.
Question 12.
The pressure exerted on the walls of the container by a gas is due to the fact that the gas molecules ……..
(a) lose their K.E
(b) Stick to the walls
(c) are accelerated towards the walls
(d) change their momenta due to collision with the walls.
Answer:
(d) change their momenta due to collision with the walls.
Question 13.
Pressure exerted by a gas is …….
(a) independent of the density of the gas
(b) inversely proportional to the density of the gas
(c) directly proportional to the density of the gas
(d) directly proportional to the square of the density of the gas.
Answer:
(c) directly proportional to the density of the gas
Question 14.
Four molecules have speed 2 km/s, 3 km/s, 4 km/s and 5 km/s. The rms speed of these molecules in km/s is …….

Answer:
(a) \(\sqrt{\frac{27}{2}}\)
Solution:
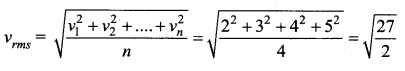
Question 15.
A real gas behaves as an ideal gas at …….
(a) low pressure and high temperature
(b) high pressure and low temperature
(c) low pressure and low temperature
(d) high pressure and high temperature.
Answer:
(a) low pressure and high temperature
![]()
Question 16.
The kinetic theory of gases breaks down most at ………
(a) low pressure and high temperature
(b) high pressure and low temperature
(c) low pressure and low temperature
(d) high pressure and high temperature.
Answer:
(b) high pressure and low temperature
Question 17.
Two different ideal gases are enclosed in two different vessels at the same pressure. If ρ1 and ρ2 are their densities and v1 and v2 their rms speeds, respectively then ____ is equal to ……

Answer:
(a) \(\sqrt{\frac{\rho_{2}}{\rho_{1}}}\)
Solution:
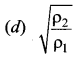
Question 18.
A cylinder of capacity 20 litres is filled with hydrogen gas. The total average K.E. of translatory motion of its molecules is 1.5 × 105 J. The pressure of hydrogen in the cylinder is …….
![]()
(d) 5 × 106 Nm-2
Solution:
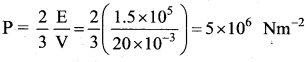
Question 19.
The molecular weights of oxygen and hydrogen are 32 and 2, respectively. The rms velocities of their molecules at a given temperatures, will be in the ratio
(a) 4 : 1
(b) 1 : 4
(e) 1 : 16
(6) 16 : 1
Answer:
(b) 1 : 4
Solution:
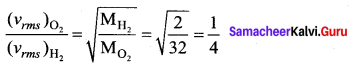
Question 20.
The average energy of a molecules of a monoatomic gas at temperature T is (K Boltzmann
constant)
(a) \(\frac{1}{2}\)kT
(b) kT
(c) \(\frac{3}{2}\)kT
(d) \(\frac{5}{2}\)kT
Answer:
(c) \(\frac{3}{2}\)kT
Question 21.
The temperature at which the molecules of nitrogen will have the same rms velocity as the
molecules of oxygen at 127° C is
(a) 77°C
(b) 350°C
(c) 273°C
(d) 457°C
Answer:
(a) 77°C
Solution:
Let the required temperature be T. Then
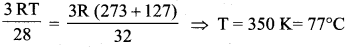 >
>
Question 22.
The temperature of a gas is raised from 27°C to 927°C. The root mean square speed of its molecules …….
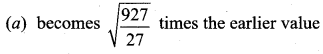
(b) gets halved
(c) remains the same
(d) gets doubled
Answer:
(d) gets doubled
Solution:
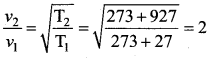
Question 23.
The temperature at which the K.E of a gas molecules is double its value at 27°C is
(a) 54°C
(b) 300 K
(c) 327°C
(d) 108°C
Answer:
(c) 327°C
Solution:
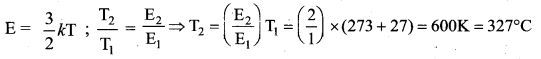
![]()
Question 24.
The temperature of an ideal gas is increased from 120 K to 480 K. If at 120 K the root mean square velocity of the gas molecules is v, at 480 K it becomes
(a) 4v
(b) 2v
(c) \(\frac{v}{2}\)
(d) \(\frac{v}{4}\)
Answer:
(b) 2v
Solution:
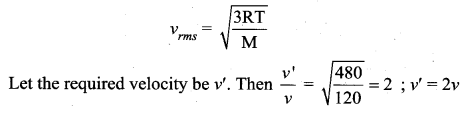
Question 25.
The average translational K.E. of O2(molar mass 32) molecules at a particular temperature is 0.048 eV. The translational K.E. of N2 (molar mass 28) molecules in eV at the same temperature is ……….
(a) 0.0015
(b) 0.003
(c) 0.048
(d) 0.768
Answer:
(c) 0.048
Solution:
Average translational K.E. of a gas molecule = \(\frac{3}{2}\)kT.
It is independent of molecular mass.
Question 26.
The K.E. of one mole of a gas at normal temperature and pressure is ![]() ……..
……..
![]()
Solution:
(d) 3.4 × 103J
Solution:
![]()
Question 27.
The average K.E. of a hydrogen gas molecule at STP will be (Boltzmann constant KB= 1.38 × 10-23 JK-1) ………
(a) 0.186 × 10-28 J
(b) 0.372 × 10-20 J
(c) 0.56 × 10-20 J
(d) 5.6 × 10-20 J
Answer:
(c) 0.56 × 10-20 J
Solution:
![]()
Question 28.
The rms speed of the particles of fume of mass 5 × 10-17 kg executing Brownian motion in air at STP is ……
(a) 1.5 ms-1
(b) 3.0 ms-1
(c) 1.5 cm s-1
(d) 3.0 cm s-1
Answer:
(c) 1.5 cm s-1
Solution:

Question 29.
To what temperature should the hydrogen at room temperature (27°C) be heated at constant pressure so that the RMS velocity of its molecules becomes double its previous value?
(a) 1200°C
(b) 927°C
(c) 600°C
(d) 108°C
Answer:
(b) 927°C
Solution:
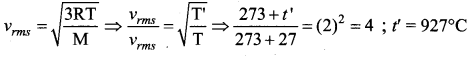
![]()
Question 30.
A vessel contains oxygen at 400 K. Another similar vessel contains an equal mass of hydrogen at 300K. The ratio of the rms speeds of molecules of hydrogen and oxygen is

Answer:
(d) \(2 \sqrt{3}\)
Solution:
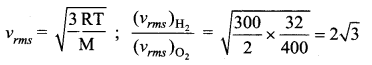
Question 31.
A chamber contains a mixture of helium gas (He) and hydrogen gas (H2). The ratio of the root- mean-square speeds of the molecules of He and H2 is ……..
(a) 2
(b) \(\sqrt{2}\)
(c) \(\frac{1}{\sqrt{2}}\)
(d) \(\frac{1}{2}\)
Answer:
(c) \(\frac{1}{\sqrt{2}}\)
Solution:
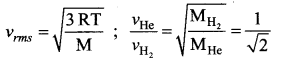
Question 32.
On colliding with the walls in a closed container, the ideal gas molecules.
(a) transfer momentum to the walls
(b) lose momentum completely
(c) move with smaller speeds
(d) perform Brownian motion.
Answer:
(a) transfer momentum to the walls
Question 33.
The speeds of 5 molecules of a gas (in arbitrary units) are as follows: 2, 3, 4, 5, 6 The root mean square speed for these molecule is
(a) 2.91
(b) 3.52
(c) 4.00
(d) 4.24
Answer:
(d) 4.24
Solution:
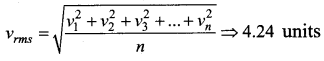
Question 34.
At absolute zero temperature, the K.E. of the molecules becomes ………
(a) zero
(b) maximum
(c) minimum
(d) none of these
Answer:
(a) zero
Question 35.
If the rms speed of the molecules of a gas is 1000 ms-1 the average speed of the molecule is
(a) 1000 ms-1
(b) 922 ms-1
(c) 780 ms-1
(d) 849 ms-1
Answer:
(b) 922 ms-1
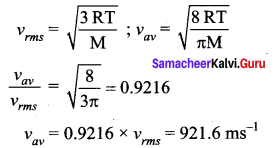
Question 36.
The gas having average molecular speed four times that of SO2 (molecular mass 64) is
(a) He (molecular mass 4)
(b) O2 (molecular mass 32)
(c) H2 (molecular mass 2)
(d) CH4 (molecular mass 16)
Answer:
(a) He (molecular mass 4)
Solution:
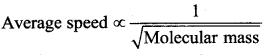
Samacheer Kalvi 11th Physics Kinetic Theory of Gases 2 Marks Questions
Question 1.
State Avogadro’s law.
Answer:
It states that equal volumes of all gases under similar conditions of temperature and pressure, contain equal number of molecules.
Question 2.
Define root mean square speed (vrms). Write down its equations.
Answer:
Root mean square speed is defined as the square root of the mean of the square of speeds of all molecules. It is denoted by ![]()
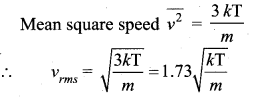
![]()
Question 3.
Define Avogadro’s number.
Answer:
It is defined as the number of particles present in one mole of the substance. It is denoted by NA
![]()
Question 4.
Define Average speed. Write it equation.
Answer:
Average speed is defined as the mean (or) average of all the speeds of molecules.
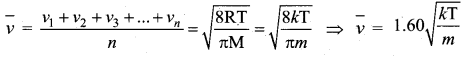
Question 5.
Define most probable speed of the gas. Write its expressions.
Answer:
It is defined as the speed acquired by most of the molecules of the gas.
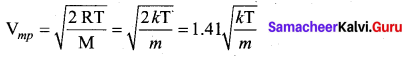
Question 6.
![]()
Answer:

Question 7.
What is the reason “No hydrogen in Earth’s atmosphere” ?
Answer:
As the root mean square speed of hydrogen is much less than that of nitrogen, it easily escapes from the earth’s atmosphere.
In fact, the presence of nonreactive nitrogen instead of highly combustible hydrogen deters
many disastrous consequences.
![]()
Question 8.
What is Brownian motion?
Answer:
The motion of the particles in a random and zig-zag mannar in a fluid is called Brownian motion.
Question 9.
What does the universal gas constant R signify? Give its value.
Answer:
The universal gas constant R signifies the workdone by (or on) a gas per mole per kelvin. Its value is R = 8.314 J mol-1 K-1
Question 10.
What is Boltzmann’s constant? Give its value.
Answer:
Boltzmann’s constant is defined as the gas constant per molecule.
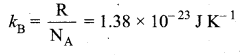
Question 11.
When do the real gases obey more correctly the gas equation: PV = nRT?
Answer:
An ideal gas is one whose molecules have zero volume and no mutual force between them. At low pressure, the volume of a gas is large and so the volume occupied by the molecules is negligible in comparison to the volume of the gas. At high temperature, the molecules have large velocities and so the intermolecular force has no influence on their motion. Hence at low pressure and high temperature, the behaviour of real gases approach the ideal gas behaviour.
Samacheer Kalvi 11th Physics Kinetic Theory of Gases Additional Numerical Problems
Question 1.
If the rms speed of hydrogen molecules at 300 K is 1930 ms-1. Then what is the rms speed of oxygen molecules
Answer:
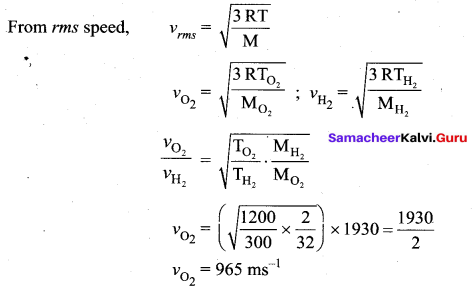
![]()
Question 2.
The rms velocity of the molecules in a sample of helium is 5/7 times that of molecules in a sample of hydrogen. If the temperature of hydrogen is 0°C. Then, what is the temperature of helium?
Answer:
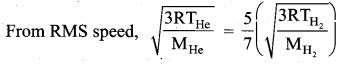
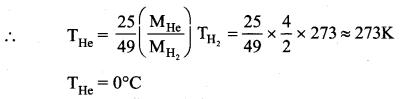
Question 3.
A cylinder of fixed capacity 44.8 litres contain helium gas at standard pressure and temperature. What is the amount of heat needed to raise the temperature of the gas by 15°C? (R = 8.31 J mol-1 K-1)
Answer:
Volume of 1 mole of He at STP = 22.4 litres
Total volume of He at STP = 44.8 litres
![]()
Molar specific heat of He (monoatomic gas) at constant volume,
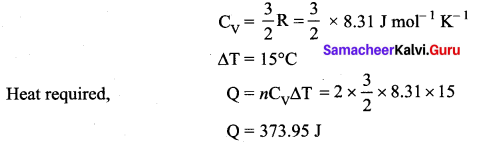
Question 4.
An insulated container containing monoatomic gas of molar mass m is moving with a velocity v0. If the container is suddenly stopped. Find the change in temperature.
Answer:
Suppose the container has n moles of the monoatomic gas. Then the loss in K.E. of the gas
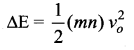
If the temperature of the gas changes by ∆T, then heat gained by the gas,

Question 5.
Estimate the total number of molecules inclusive of oxygen, nitrogen, water vapour and other constituents in a room of capacity 25.0 m3 at a temperature of 27°C and 1 atmospheric pressure. (kB = 1.38 × 10-23 JK-1)
Solution:


![]()
Question 6.
Estimate the average energy of a helium atom at
(i) room temperature (27°C)
(ii) the temperature on the surface of the sun (6000 K) and
(iii) the temperature of 107 K. (kB = 1.38 × 10-23JK-1)
Answer:

Question 7.
The molecules of a given mass of a gas have rms velocity of 200 ms 1 at 27°C and 1.0 × 10s Nm-2 pressure. When the temperature and pressure of the gas are respectively. 127 °C and 0.05 × 10s Nm-2.
Find the rms velocity of its molecules in ms-1
Answer:

Question 8.
At what temperature will the rms speed of oxygen molecules become just sufficient for escaping from the Earth’s atmosphere? (Mass of oxygen molecule (m) = 2.76 × 10-26 kg
Boltzmann’s constant (kB) = 1.38 × 10-23 JK-1)
Answer:
![]()

![]()
Question 9.
The temperature of a gas is raised from 27°C to 927°C. What is the rms molecular speed?
Answer:

Question 10.
A gaseous mixture consists of 16 g of helium and 16 g of oxygen. Find the ratio \(\frac{\mathbf{C}_{\mathbf{P}}}{\mathbf{C}_{\mathbf{V}}}\) of the
mixture.
Answer:
