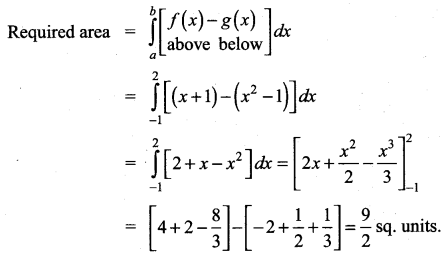Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.8

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.8

Question 1.
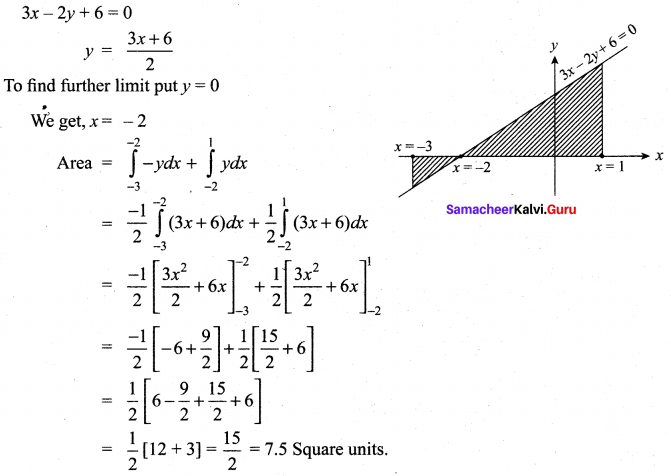
Find the area of the region bounded by 3x – 2y + 6 = 0, x = -3, x = 1 and x-axis.
Solution:

Question 2.
Find the area of the region bounded by 2x – y + 1 = 0, y = – 1, y = 3 and y – axis.
Solution:
2x – y + 1 = 0

To find further limit put x = 0, we get y = 1

Question 3.
Find the area of the region bounded by the curve 2 + x – x² + y = 0, x – axis, x = -3 and x = 3.
Solution:

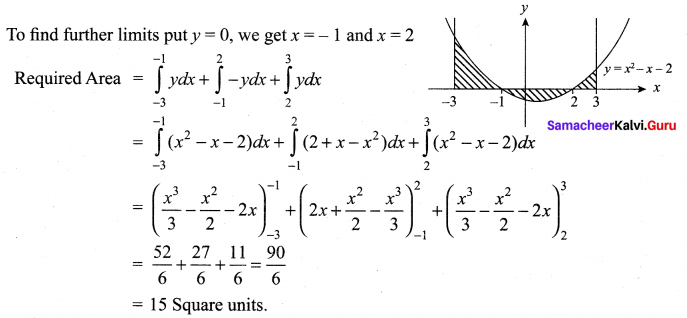
Question 4.
Find the area of the region bounded by the line y = 2x + 5 and the parabola y = x² – 2x.
Solution:
To find point of intersection of the curves
y = 2x + 5 and y = x² – 2x we get (-1, 3) and (5, 15)

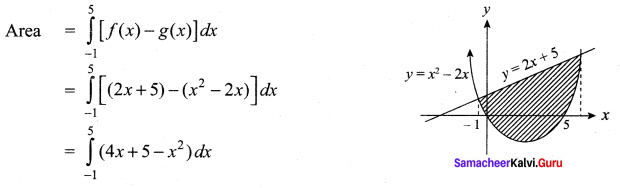
Question 5.
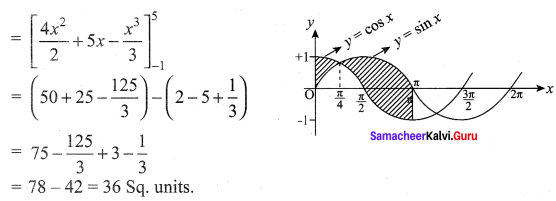
Find the area of the region bounded between the curves y = sin x and y = cos x and the lines x = 0 and x = π.
Solution:
To find the points of intersection,

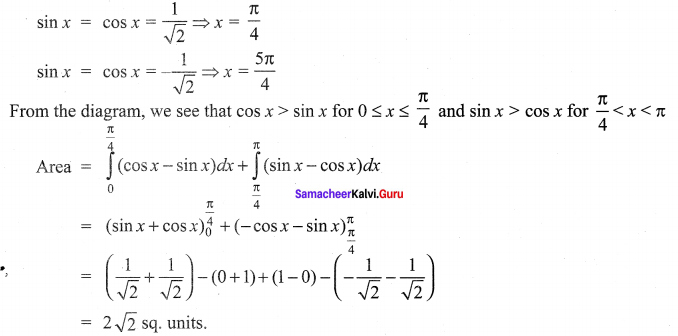
Question 6.
Find the area of the region bounded by y = tan x, y = cot x and the line x = 0, x = \(\frac{\pi}{2}\), 0
Solution:
To find the points of intersection of these two curves between 0 to \(\frac{\pi}{2}\) is \(\frac{\pi}{4}\)

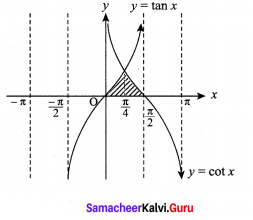
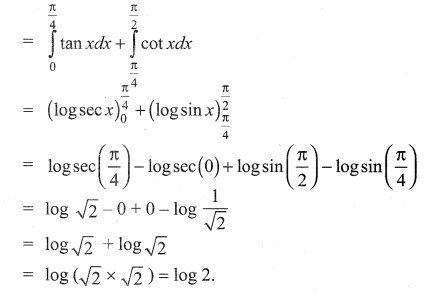
Question 7.
Find the area of the region bounded by parabola y² = x and the line y = x – 2
Solution:
To find the points of intersection solve the two equations y² = x and y = x – 2

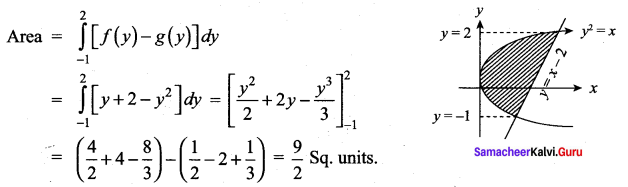
Question 8.
Father of a family wishes to divide his square field bounded by x = 0, x = 4 , y = 4 and y = 0 along the curve y² = 4x and x² = 4y into three equal parts for his wife, daughter and son. Is it possible to divide? If so, find the area to be divided among them.
Solution:
To find the points of intersection of the two curves, y² = 4x and x² = 4y are (0, 0) and (4, 4).
Area of the square field = 4 × 4 = 16 sq. units

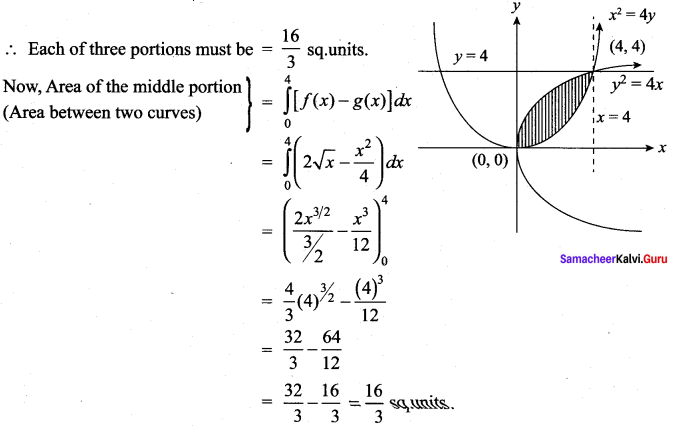
So, the remaining each of the two parts must be \(\frac{16}{3}\) sq.units.
∴ Yes, It is possible to divide the square field into three equal parts.

Question 9.
The curves = (x – 2)² + 1 has a minimum point at P. A point Q on the curve is such that the slope of PQ is 2. Find the area bounded by the curve and the chord PQ.
Solution:
y = (x – 2)² + 1



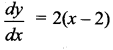
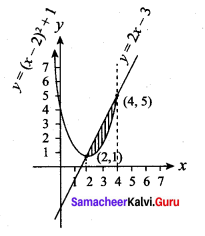
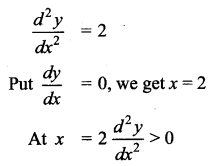
∴ x = 2 is a minimum point
∴ The point P is (2, 1)
But slope of PQ is 2
∴ Equation of the chord PQ
y – y₁ = m(x – x₁)
y – 1 = 2 (x – 2)
y – 1 = 2x – 4
y = 2x – 3
On solving the curve and line we get the point Q(4, 5)

Question 10.
Find the area of the region common to the circle x² + y² = 16 and the parabola y² = 6x.
Solution:
To find points of intersection of x² + y² = 16 and y² = 6x are (2, \(2 \sqrt{3})\)) and (2, –\(2 \sqrt{3})\))
Due to symmetrical property,

Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.8 Additional Problems

Question 1.
Find the area of the region enclosed by y² = x and y = x – 2.
Solution:
The points of intersection of the parabola y² = x and the line y = x – 2 are (1, -1) and (4, 2)

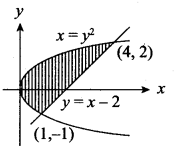
To compute the region [shown in the figure] by integrating with respect to x, we would have to split the region into two parts, because the equation of the lower boundary changes at x = 1. However, if we integrate with respect to no splitting is necessary.

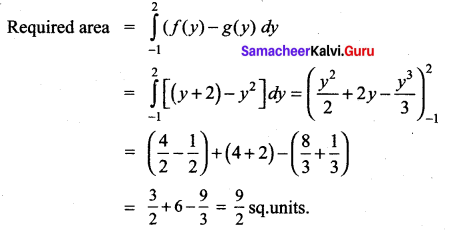
Question 2.
Find the area bounded by the curve y = x³ and the line y = x.
Solution:
The line y = x lies above the curve y = x³ in the first quadrant and y = x³ lies above the line y = x in the third quadrant. To get the points of intersection, solve the curves y = x³, y = x ⇒ x³ = x. We get x = {0, ± 1}

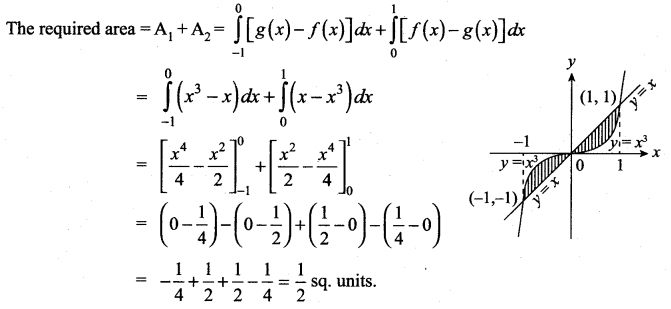
Question 3.
Find the area of the loop of the curve 3ay² = x (x – a)².
Solution:
Put y = 0; we get x = 0, a
It meets the x – axis at x = 0 and x = a
∴ Here a loop is formed between the points (0, 0) and (a, 0) about the x-axis.
Since the curve is symmetrical about the x-axis, the area of the loop is twice the area of the portion above the x-axis.

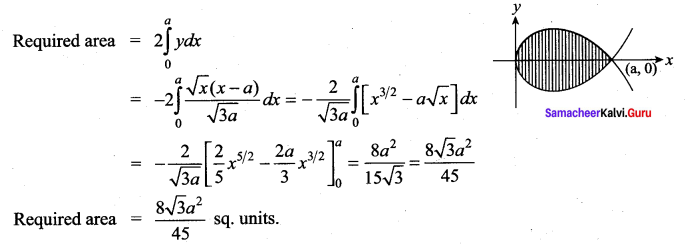
Question 4.
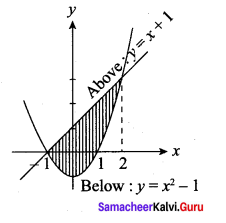
Find the area between the line y = x + 1 and the curve y = x² – 1.
Solution:
To get the points of intersection of the curves we should solve the equations y = x + 1 and y = x² – 1.
we get, x² – 1 = x + 1
x² – x – 2 = 0 ⇒ (x – 2)(x + 1) = 0
x = – 1 or x = 2
∴ The line intersects the curve at x = – 1 and x = 2.