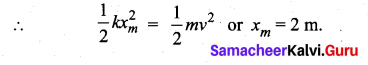Samacheer Kalvi 11th Physics Solutions Chapter 4 Work, Energy and Power

Students can Download Physics Chapter 4 Work, Energy and Power Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Physics Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 4 Work, Energy and Power

Samacheer Kalvi 11th Physics Work, Energy and Power Textual Questions Solved

Samacheer Kalvi 11th Physics Work, Energy and Power Multiple Choice Questions
Question 1.
A uniform force of (\(2 \hat{i}+\hat{j}\)) + N acts on a particle of mass 1 kg. The particle displaces from position \((3 \hat{j}+\hat{k})\) m to \((5 \hat{i}+3 \hat{j})\) m. Th e work done by the force on the particle is
[AIPMT model 2013]
(a) 9 J
(b) 6 J
(c) 10 J
(d) 12 J
Answer:
(c) 10 J

Question 2.
A ball of mass 1 kg and another of mass 2 kg are dropped from a tall building whose height is 80 m. After, a fall of 40 m each towards Earth, their respective kinetic energies will be in the ratio of [AIPMT model 2004]
(a) \(\sqrt{2}\) : 1
(b) 1 : \(\sqrt{2}\)
(c) 2 : 1
(d) 1 : 23
Answer:
(d) 1 : 23

Question 3.
A body of mass 1 kg is thrown upwards with a velocity 20 m s^-1. It momentarily comes to rest after attaining a height of 18 m. How much energy is lost due to air friction?
(Take g = 10 ms^-2) [AIPMT 2009]
(a) 20 J
(b) 30 J
(c) 40 J
(d) 10 J
Answer:
(a) 20 J

Question 4.
An engine pumps water continuously through a hose. Water leaves the hose with a velocity v and m is the mass per unit length of the water of the jet. What is the rate at which kinetic energy is imparted to water ? [AIPMT 2009]

Answer:
(a) \(\frac{1}{2} m v^{2}\)

Question 5.
A body of mass 4 m is lying in xv-plane at rest. It suddenly explodes into three pieces. Two pieces each of mass m move perpendicular to each other with equal speed v the total kinetic energy generated due to explosion is [AIPMT 2014]

Answer:
(b) \(\frac{3}{2} m v^{2}\)

The potential energy calculator to find how much energy is stored in an object raised off the ground.

Question 6.
The potential energy of a system increases, if work is done
(a) by the system against a conservative force
(b) by the system against a non-conservative force
(c) upon the system by a conservative force
(d) upon the system by a non-conservative force
Answer:
(a) by the system against a conservative force

Question 7.
What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?

Answer:
(c) \(\sqrt{5 g R}\)

Question 8.
The work done by the conservative force for a closed path is
(a) always negative
(b) zero
(c) always positive
(d) not defined
Answer:
(b) zero

Question 9.
If the linear momentum of the obj ect is increased by 0.1 %, then the kinetic energy is increased by
(a) 0.1%
(b) 0.2%
(c) 0.4%
(d) 0.01%
Answer:
(b) 0.2%

Question 10.
If the potential energy of the particle is 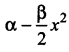, then force experienced by the particle is

Answer:
(c) F = -βx

Question 11.
A wind-powered generator converts wind energy into electric energy. Assume that the generator converts a fixed fraction of the wind energy intercepted by its blades into electrical energy. For wind speed v, the electrical power output will be proportional to
(a) v
(b) v²
(c) v³
(d) v⁴
Answer:
(c) v⁴

Question 12.
Two equal masses m₁ and m₂ are moving along the same straight line with velocities 5 ms^-1 and -9 ms^-1 respectively. If the collision is elastic, then calculate the velocities after the collision of Wj and m2, respectively
(a) -4 ms^-1 and 10 ms^-1
(b) 10 ms^-1 and 0 ms^-1
(c) -9 ms^-1 and 5 ms^-1
(d) 5 ms^-1 and 1 ms^-1
Answer:
(c) -9 ms^-1 and 5 ms^-1

Question 13.
A particle is placed at the origin and a force F = kx is acting on it (where k is a positive constant). If U(0) = 0, the graph of U(x) versus x will be (where U is the potential energy function) [IIT 2004]

Answer:

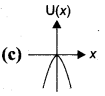
Question 14.
A particle which is constrained to move along x-axis, is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x) = -kx + ax³. Here, k and a are positive constants. For x ≥ 0, the functional form of the potential energy U(x) of the particle is [IIT 2002]

Answer:

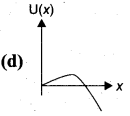
Question 15.
A spring of force constant k is cut into two pieces such that one piece is double the length of the other. Then, the long piece will have a force constant of

Answer:
(b) \(\frac{3}{2} k\)

Samacheer Kalvi 11th Physics Work, Energy and Power Short Answer Questions

Question 1.
Explain how the definition of work in physics is different from general perception.
Answer:
The term work is used in diverse contexts in daily life. It refers to both physical as well as mental work. In fact, any activity can generally be called as work. But in Physics, the.term work is treated as a physical quantity with a precise definition. Work is said to be done by the force when the force applied on a body displaces it.

Question 2.
Write the various types of potential energy. Explain the formulae.
Answer:
(a) U = mgh
U – Gravitational potential energy
m – Mass of the object,
g – acceleration due to gravity
h – Height from the ground,

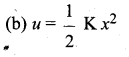
u – Elastic potential energy
k – String constant; x-displacement.

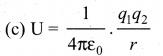
U – electrostatic potential energy
\(\varepsilon_{0}\) = absolute permittivity
q₁, q₂ – electric charges

Question 3.
Write the differences between conservative and non-conservative forces. Give two examples each.
Answer:

Question 4.
Explain the characteristics of elastic and inelastic collision.
Answer:
In any collision process, the total linear momentum and total energy are always conserved whereas the total kinetic energy need not be conserved always. Some part of the initial kinetic energy is transformed to other forms of energy. This is because, the impact of collisions and deformation occurring due to collisions may in general, produce heat, sound, light etc. By taking these effects into account, we classify the types of collisions as follows:
(a) Elastic collision
(b) Inelastic collision
(a) Elastic collision: In a collision, the total initial kinetic energy of the bodies (before collision) is equal to the total final kinetic energy of the bodies (after collision) then, it is called as elastic collision, i.e.,
Total kinetic energy before collision = Total kinetic energy after collision
(b) Inelastic collision: In a collision, the total initial kinetic energy of the bodies (before collision) is not equal to the total final kinetic energy of the bodies (after collision) then, it is called as inelastic collision, i.e.,
Total kinetic energy before collision ≠ Total kinetic energy after collision

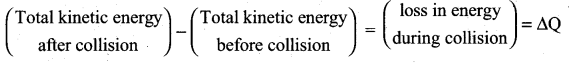
Even though kinetic energy is not conserved but the total energy is conserved. This is because the total energy contains the kinetic energy term and also a term ∆Q, which includes all the losses that take place during collision. Note that loss in kinetic energy during collision is transformed to another form of energy like sound, thermal, etc. Further, if the two colliding bodies stick together after collision such collisions are known as completely inelastic collision or perfectly inelastic collision. Such a collision is found very often. For example when a clay putty is thrown on a moving vehicle, the clay putty (or Bubblegum) sticks to the moving vehicle and they move together with the same velocity.

Question 5.
Define the following
(a) Coefficient of restitution
(b) Power
(c) Law of conservation of energy
(d) Loss of kinetic energy in inelastic collision.
Answer:
(a) The ratio of velocity of separation after collision to the velocity of approach before collision

(b) Power is defined as the rate of work done or energy delivered

Its unit is watt.
(c) The law of conservation of energy states that energy can neither be created nor destroyed. It may be transformed from one form to another but the total energy of an isolated system remains constant.
(d) In perfectly inelastic collision, the loss in kinetic energy during collision is transformed to another form of energy like sound, thermal, heat, light etc. Let KE_i be the total kinetic energy before collision and KE_f be the total kinetic energy after collision.
Total kinetic energy before collision,

Total kinetic energy after Collision,

Then the loss of kinetic energy is

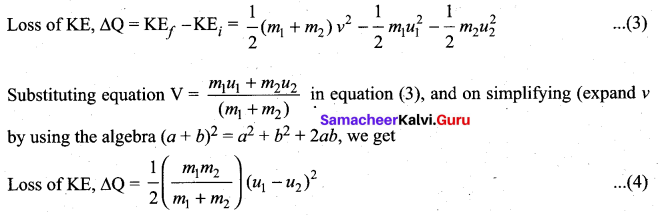
Samacheer Kalvi 11th Physics Work, Energy and Power Long Answer Questions

Question 1.
Explain with graphs the difference between work done by a constant force and by a variable force.
Answer:
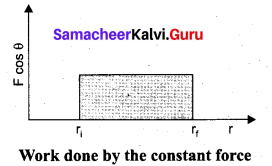
Work done by a constant force: When a constant force F acts on a body, the small work done (dW) by the force in producing a small displacement dr is given by the relation,
dW = (F cos θ) dr ..(1)
The total work done in producing a displacement from initial position r_i to final position r_f is,

The graphical representation of the work done by a constant force is shown in figure given below. The area under the graph shows the work done by the constant force.

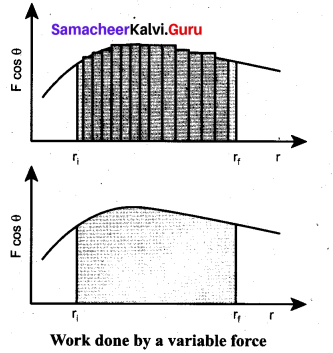
Work done by a variable force: When the component of a variable force F acts on a body, the small work done (dW) by the force in producing a small displacement dr is given by the relation
dW = F cos θ dr [F cos θ is the component of the variable force F]
where, F and θ are variables. The total work done for a displacement from initial position r_i to final position r_f is given by the relation,

A graphical representation of the work done by a variable force is shown in figure given below. The area under the graph is the work done by the variable force.

Question 2.
State and explain work energy principle. Mention any three examples for it.
Answer:
(i) If the work done by the force on the body is positive then its kinetic energy increases.
(ii) If the work done by the force on the body is negative then its kinetic energy decreases.
(iii) If there is no work done by the force on the body then there is no change in its kinetic energy, which means that the body has moved at constant speed provided its mass remains constant.
(iv) When a particle moves with constant speed in a circle, there is no change in the kinetic energy of the particle. So according to work energy principle, the work done by centripetal force is zero.

Question 3.
Arrive at an expression for power and velocity. Give some examples for the same.
Answer:
The work done by a force \(\overrightarrow{\mathrm{F}}\) for a displacement \(d \vec{r}\) is

Left hand side of the equation (i) can be written as

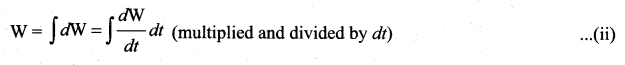
Since, velocity is 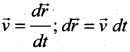. Right hand side of the equation (i) can be written as dt

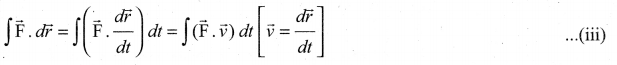
Substituting equation (ii) and equation (iii) in equation (i), we get

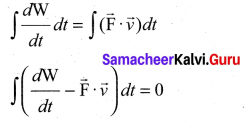
This relation is true for any arbitrary value of dt. This implies that the term within the bracket must be equal to zero, i.e.,

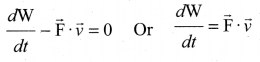
Hence power \(\mathrm{P}=\overrightarrow{\mathrm{F}} \cdot \vec{v}\)

Question 4.
Arrive at an expression for elastic collision in one dimension and discuss various cases.
Answer:
Consider two elastic bodies of masses m₁ and m₂ moving in a straight line (along positive x direction) on a frictionless horizontal surface as shown in figure given below.

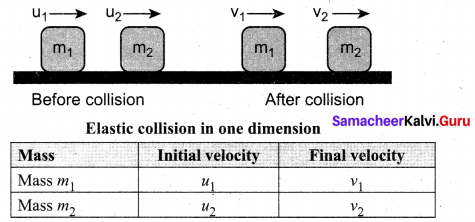
In order to have collision, we assume that the mass m] moves faster than mass m₂ i.e., u₁ > u₂. For elastic collision, the total linear momentum and kinetic energies of the two bodies before and after collision must remain the same.

From the law of conservation of linear momentum,
Total momentum before collision (p_i) = Total momentum after collision (p_f)
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ …(i)


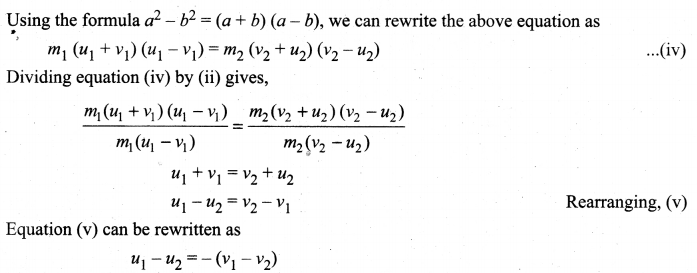
This means that for any elastic head on collision, the relative speed of the two elastic bodies after the collision has the same magnitude as before collision but in opposite direction. Further note that this result is independent of mass.
Rewriting the above equation for v₁ and v₂,
v₁ = v₂ + u₂ – u₂ …(vi)
Or v₂ = u₁ + v₁ – u₂ …(vii)
To find the final velocities v₁ and v₂:
Substituting equation (vii) in equation (ii) gives the velocity of as m₁ as
m₁ (u₁ – v₁) = m₂(u₁ + v₁ – u₂ – u₂)
m₁ (u₁ – y₁) = m₂ (u₁ + + v₁  – 2u₂)
m₁u₁ – m₁v₁ = m₂u₁ + m₂v₁ + 2m₂u₂
m₁u₁ – m₂u₁ + 2m₂u₂ = m₁v₁ + m₂v₁
(m₁– m₂) u₁ + 2m₂u₂ = (m₁ + m₂) v₁

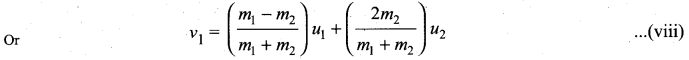
Similarly, by substituting (vi) in equation (ii) or substituting equation (viii) in equation (vii), we get the final velocity of m₂ as

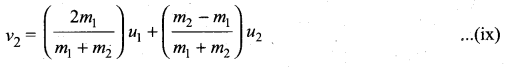
Case 1: When bodies has the same mass i.e., m₁ = m₂,

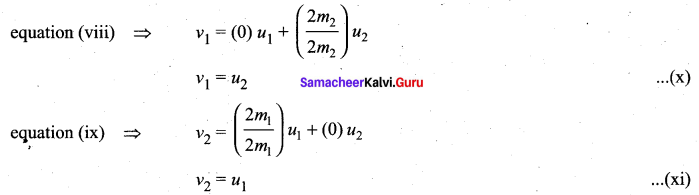
The equations (x) and (xi) show that in one dimensional elastic collision, when two bodies of equal mass collide after the collision their velocities are exchanged.
Case 2: When bodies have the same mass i.e., m₁ = m₂ and second body (usually called target) is at rest (u₂ = 0),
By substituting m₁ = m₂ = and u₂ = 0 in equations (viii) and equations (ix) we get,
from equation (viii) ⇒ v₁ = 0 …(xii)
from equation (ix) ⇒ v₂ = u₁ ….. (xiii)
Equations (xii) and (xiii) show that when the first body comes to rest the second body moves with the initial velocity of the first body.
Case 3: The first body is very much lighter than the second body

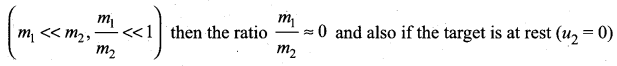
Dividing numerator and denominator of equation (viii) by m₂, we get

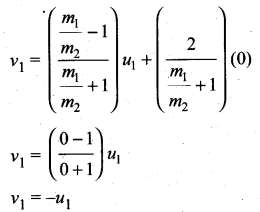
Similarly the numerator and denominator of equation (ix) by m₂, we get

The equation (xiv) implies that the first body which is lighter returns back (rebounds) in the opposite direction with the same initial velocity as it has a negative sign. The equation (xv) implies that the second body which is heavier in mass continues to remain at rest even after collision. For example, if a ball is thrown at a fixed wall, the ball will bounce back from the wall with the same velocity with which it was thrown but in opposite direction.

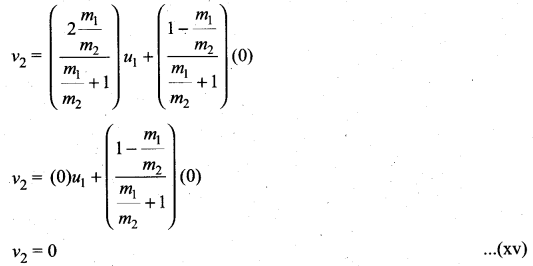
Dividing numerator and denominator of equation (xiii) by m₁, we get

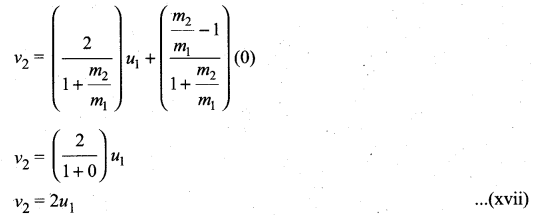
The equation (xvi) implies that the first body which is heavier continues to move with the same initial velocity. The equation (xvii) suggests that the second body which is lighter will move with twice the initial velocity of the first body. It means that the lighter body is thrown away from the point of collision.

Question 5.
What is inelastic collision? In which way it is different from elastic collision. Mention few examples in day to day life for inelastic collision.
Answer:
Inelastic collision: In a collision, the total initial kinetic energy of the bodies (before collision) is not equal to the total final kinetic energy of the bodies (after collision) then, it is called as inelastic collision, i.e.,
Total kinetic energy before collision ≠ Total kinetic energy after collision

Even though kinetic energy is not conserved but the total energy is conserved. This is because the total energy contains the kinetic energy term and also a term ∆Q, which includes all the losses that take place during collision. Note that loss in kinetic energy during collision is transformed to another form of energy like sound, thermal, etc. Further, if the two colliding bodies stick together after collision such collisions are known as completely inelastic collision or perfectly inelastic collision. Such a collision is found very often. For example when a clay putty is thrown on a moving vehicle, the clay putty (or Bubblegum) sticks to the moving vehicle and they move together with the same velocity.
Difference between Elastic & in elastic collision

Samacheer Kalvi 11th Physics Numerical Problems

Question 1.
Calculate the work done by a force of 30N in lifting a load of 2 Kg to a height of 10m(g = 10 ms^-1)
Answer:
Given: F = 30 N, load (m) = 2 kg; height = 10 m, g = 10 ms^-2
Gravitational force F = mg = 30 N
The distance moved h = 10 m
Work done on the object W = Fh = 30 × 10 = 300 J.

Question 2.
A ball with a velocity of 5 ms^-1 impinges at angle of 60° with the vertical on a smooth horizontal plane. If the coefficient of restitution is 0.5, find the velocity and direction after the impact.
Answer:
Given: Velocity of ball: 5 ms^-1
Angle of inclination with vertical: 60°
Coefficient of restitution = 0.5.
Note: Let the angle reflection is θ’ and the speed after collision is v’. The floor exerts a force on the ball along the normal during the collision. There is no force
parallel to the surface. Thus, the parallel component of the velocity of the ball remains unchanged. This gives
v’ sin θ’ = v sin θ …… (i)
Vertical component with respect to floor = v’ cos θ’ (velocity of separation)
Velocity of approach = v cos θ


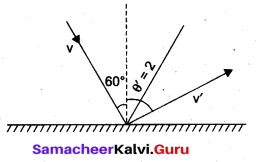
from (i) and (ii)

Question 3.
A bob of mass m is attached to one end of the rod of negligible mass and length r, the other end of which is pivoted freely at a fixed center O as shown in the figure.
What initial speed must be given to the object to reach the top of the circle?
(Hint: Use law of conservation of energy). Is this speed. less or greater than speed obtained in the section 4.2.9?

Answer:
To get the vertical speed given to the object to reach the top of the circle, law of conservation of energy can be used at a points (1) and (2)
Total energy at 1 = Total energy at 2
∴ Potential energy at point 1 = 0

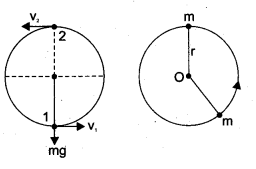
from eqn (i)

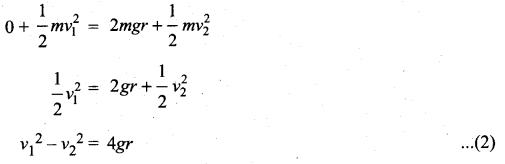
In this case bob of mass m is connected with a rod of negligible mass, so the velocity of bob at highest point can be equal to zero i.e. v₂ = 0

The speed of bob obtained here is lesser than the speed obtained in section 4.2.9. It is only because of string is replaced by a massless rod here.

Question 4.
Two different unknown masses A and B collide. A is initially at rest when B has a speed v. After collision B has a speed v/2 and moves at right angles to its original direction of motion. Find the direction in which A moves after collision.
Answer:

Question 5.
A bullet of mass 20 g strikes a pendulum of mass 5 kg. The centre of mass of pendulum rises a vertical distance of 10 cm. If the bullet gets embedded into the pendulum, calculate its initial speed.
Answer:
Given: m₁ = 20 g = 20 × 10^-3 kg; m₂ = 5 kg; s = 10 × 10^-2 m.
Let the speed of the bullet be v. The common velocity of bullet and pendulum bob is V. According to law of conservation of linear momentum.

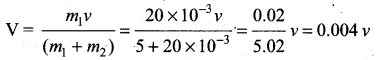
The bob with bullet go up with a deceleration of g = 9.8 ms^-2. Bob and bullet come to rest at a height of 10 × 10^-2 m.
from III rd equation of motion

Samacheer Kalvi 11th Physics Conceptual Questions

Question 1.
A spring which in initially in un-stretched condition, is first stretched by a length x and again by a further length x. The work done in the first case W₁ is one third of the work done in second case W₂. True or false?
Answer:
The amount of work done to stretching distance x

Total work done in stretching the spring through a distance 2x is

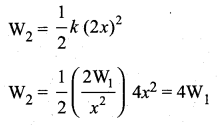
Extra work required to stretch the additional x distance is
W = W₂ – W₁ = 4W₁ – W₁ = 3W₁

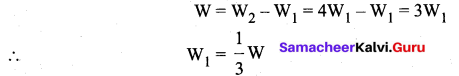
Hence it is true

Question 2.
Which is conserved in inelastic collision? Total energy (or) Kinetic energy?
Answer:
In inelastic collision total energy is only conserved but kinetic energy is not conserved. A part of kinetic energy is converted into some other form of energy such as sound, heat energy.
Note: The linear momentum is also conserved.

Question 3.
Is there any net work done by external forces on a car moving with a constant speed along a straight road?
Answer:
If the car moves at constant speed, then there is no change in its kinetic energy. It implies that if there is no change in kinetic energy then there is no work done by the force on the body provided its mass remains constant.

Question 4.
A car starts from rest and moves on a surface with uniform acceleration. Draw the graph of kinetic energy versus displacement. What information you can get from that graph?
Answer:
A car starts from rest and moves with uniform acceleration. The graph between kinetic energy and displacement, is a straight line.
The slope of KE and displacement graph gives net force acting on the car to keep the car with uniform acceleration.

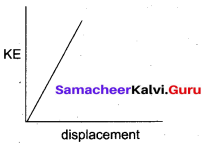
Question 5.
A charged particle moves towards another charged particle. Under what conditions the total momentum and the total energy of the system conserved?
Answer:
Coulomb force is acting in between the charged particles Internal force is a conservative force. If no external forces act or the work done by external forces is zero then the mechanical energy of the system and also total linear momentum also remains constant.

Samacheer Kalvi 11th Physics Work, Energy and Power Additional Questions Solved

Samacheer Kalvi 11th Physics Multiple Choice Questions

Question 1.
Thrust and linear momentum
(a) Thrust and linear momentum
(b) Work and energy
(c) Work and power
(d) Power and energy
Answer:
(b) Work and energy

Question 2.
The rate of work done is called as
(a) energy
(b) power
(c) force
(d) mechanical energy
Answer:
(b) power

Question 3.
Unit of work done
(a) Nm
(b) joule
(c) either a or b
(d) none
Answer:
(c) either a or b

Question 4.
Dimensional formula for work done is
(a) MLT^-1
(b) ML²T²
(c) M^-1L^-1T²
(d) ML²T^-2
Answer:
(d) ML²T^-2

Question 5.
When a body moves on a horizontal direction, the amount of work done by the gravitational force is
(a) positive
(b) negative
(c) zero
(d) infinity
Answer:
(c) zero

Question 6.
The amount of work done by centripetal force on the object moving in a circular path is
(a) zero
(b) infinity
(c) positive
(d) negative
Answer:
(a) zero

Question 7.
The work done by the goal keeper catches the ball coming towards him by applying a force is
(a) positive
(b) negative
(c) zero
(d) infinity
Answer:
(b) negative

Question 8.
If the angle between force and displacement is acute then the work done is
(a) positive
(b) negative
(c) zero
(d) maximum
Answer:
(a) positive

Question 9.
If the force and displacement are perpendicular to each other, then the work done is
(a) positive
(b) negative
(c) zero
(d) maximum
Answer:
(c) zero

Question 10.
If the angle between force and displacement is obtuse, then the work done is
(a) positive
(b) negative
(c) zero
(d) minimum
Answer:
(b) negative

Question 11.
The area covered under force and displacement graph is
(a) work done
(b) acceleration
(c) power
(d) kinetic energy
Answer:
(a) work done

Question 12.
The capacity to do work is
(a) force
(b) energy
(c) work done
(d) power
Answer:
(b) energy

Question 13.
The energy possessed by a body due to its motion is called as
(a) potential energy
(b) kinetic energy
(c) mechanical energy
(d) none
Answer:
(b) kinetic energy

Question 14.
The energy possessed by the body by virtue of its position is called as
(a) potential energy
(b) kinetic energy
(c) mechanical energy
(d) none
Answer:
(a) potential energy

Question 15.
1 erg is equivalent to
(a) 10^-7 J
(b) 1.6 × 10^-19 J
(c) 4.186 J
(d) 3.6 × 10^-6 J
Answer:
(a) 10^-7 J

Question 16.
1 electron volt is equivalent to
(a) 10^-7 J
(b) 1.6 × 10^-19 J
(c) 4.186 J
(d) 3.6 × 10^-6 J
Answer:
(b) 1.6 × 10^-19 J

Question 17.
1 kilowatt hour is equivalent to
(a) 10^-7 J
(b) 1.6 × 10^-19 J
(c) 4.186 J
(d) 3.6 × 10^-6 J
Answer:
(d) 3.6 × 10^-6 J

Question 18.
1 calorie is equivalent to
(a) 10^-7 J
(b) 1.6 × 10^-19 J
(c) 4.186 J
(d) 3.6 × 10⁶ J
Answer:
(c) 4.186 J

Question 19.
The amount of work done by a moving body depends on the
(a) mass of the body
(b) velocity
(c) both (a) and (b)
(d) time
Answer:
(c) both (a) and (b)

Question 20.
The kinetic energy of a body is given by

Answer:
(a) \(\frac{1}{2} m v^{2}\)

Question 21.
Kinetic energy of the body is always
(a) zero
(b) infinity
(c) negative
(d) positive
Answer:
(d) positive

Question 22.
If the work done by the force on the body is positive then its kinetic energy
(a) increases
(b) decreases
(c) zero
(d) either increases or decreases
Answer:
(a) increases

Question 23.
If p is the momentum of the particle then its kinetic energy is

Answer:
(c) \(\frac{\mathbf{p}^{2}}{2 \mathbf{m}}\)

Question 24.
If two objects of masses m₁ and m₂ (m₁ > m₂) are moving with the same momentum then the kinetic energy will be greater for
(a) m₁
(b) m₂
(c) m₁ or m₂
(d) both will have equal kinetic energy
Answer:
(b) m₂

Question 25.
For a given momentum, the kinetic energy is proportional to

Answer:
(b) \(\frac{1}{\mathrm{m}}\)

Question 26.
Elastic potential energy possessed by a spring is

Answer:
(c) \(\frac{1}{2}\)kx²

Question 27.
Potential energy stored in the spring depends on
(a) spring constant
(b) mass
(c) gravity
(d) length
Answer:
(b) mass

Question 28.
Two springs of spring constants k₁ and k₂ (k₁ > k₂). If they are stretched by the same force then (u₁, u₂ are potential energy of the springs) is
(a) u₁ > u₂
(b) u₂ > u₁
(c) u₁ = u₂
(d) u₁ ≥ u₂
Answer:
(b) u₂ > u₁

Question 29.
Conservative force is
(a) electrostatic force
(b) magnetic force
(c) gravitational force
(d) all the above
Answer:
(d) all the above

Question 30.
Non conservative force is
(a) frictional force
(b) viscous force
(c) air resistance
(d) all the above
Answer:
(d) all the above

Question 31.
If the work done is completely recoverable, then the force is
(a) conservative
(b) non-conservative
(c) both (a) and (b)
(d) frictional in nature
Answer:
(b) non-conservative

Question 32.
The work done by the conservative forces in a cycle is
(a) zero
(b) one
(c) infinity
(d) having negative value
Answer:
(a) zero

Question 33.
Negative gradient of potential energy gives
(a) conservative force
(b) non conservative force
(c) kinetic energy
(d) frictional force
Answer:
(a) conservative force

Question 34.
When a particle moving in a vertical circle, the variable is/are
(a) velocity of the particle
(b) tension of the string
(c) both (a) and (b)
(d) mass of the particle
Answer:
(c) both (a) and (b)

Question 35.
Which of the following is zero at the highest point in vertical circular motion?
(a) velocity of the particle
(b) tension of the spring
(c) potential energy
(d) none
Answer:
(a) velocity of the particle

Question 36.
The body must have a speed at highest point in vertical circular motion to stay in the circular path

Answer:
(a) \(\geq \sqrt{\mathbf{g r}}\)

Question 37.
The body must have a minimum speed of lowermost point in vertical circular motion to complete the circle

Answer:
(c) \(\geq \sqrt{5 \mathrm{gr}}\)

Question 38.
The rate of work done is
(a) energy
(b) force
(c) power
(d) energy flow
Answer:
(c) power

Question 39.
The unit of power is
(a) J
(b) W
(c) J s^-1
(d) both (b) and (c)
Answer:
(d) both (b) and (c)

Question 40.
One horse power (1 hp) is
(a) 476 W
(b) 674 W
(c) 746 W
(d) 764 W
Answer:
(c) 746 W

Question 41.
The dimension of power is
(a) ML²T^-2
(b) ML²T^-3
(c) ML^-2T²
(d) ML^-2T³
Answer:
(b) ML²T^-3

Question 42.
kWh is the practical unit of
(a) energy
(b) power
(c) electrical energy
(d) none
Answer:
(a) energy

Question 43.
If a force F is applied on a body and the body moves with velocity v, the power will be
(a) F.V
(b) F/V
(c) FV²
(d) FW²
Answer:
(a) F.V

Question 44.
A body of mass m is thrown vertically upward with a velocity v. The height at which the kinetic energy of the body is one third of its initial value is given by

Answer:
(c) \(\frac{v^{2}}{6 g}\)
Solution:
Initial 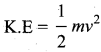. The loss in K.E will be the gain in potential energy

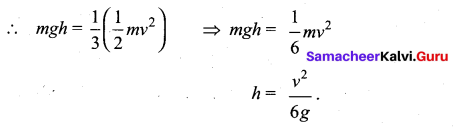
Question 45.
A body of mass 5 kg is initially at rest. By applying a force of 20 N at an angle of 60° with horizontal the body is moved to a distance of 4 m. The kinetic energy acquired by the body is
(a) 80 J
(b) 60 J
(c) 40 J
(d) 17.2 J
Answer:
(c) 40 J
Solution:
The work done is equal to its kinetic energy
∴ K.E gained = Fs cos θ = 20 × 4 cos 60° = 40 J.

Question 46.
A bullet is fired normally on an immovable wooden plank of thickness 2 m. It loses 20% of its kinetic energy in penetrating a thickness 0.2 m of the plank. The distance penetrated by the bullet inside the wooden plank is
(a) 0.2 m
(b) 0.8 m
(c) 1 m
(d) 1.5 m
Answer:
(c) 1 m
Solution:
The wood offers a constant retardation. If the bullet loses 20% of its kinetic energy by penetrating 0.2m. it can penetrate further into 4 × 0.2 = 0.8 m with the remaining kinetic energy. So the total distance penetrated by the bullet is 0.2 + 0.8 = 1 m.

Question 47.
Which of the following quantity is conserved in all collision process?
(a) kinetic energy
(b) linear momentum
(c) both (a) and (b)
(d) none.
Answer:
(b) linear momentum

Question 48.
The kinetic energy is conserved in
(a) elastic collision
(b) inelastic collision
(c) both (a) and (b)
(d) none
Answer:
(a) Elastic collision

Question 49.
The kinetic energy is not conserved in
(a) Elastic collision
(b) In elastic collision
(c) both (a) and (b)
(d) none
Answer:
(b) In elastic collision

Question 50.
In inelastic collision, which is conserved
(a) linear momentum
(b) total energy
(c) both (a) and (b)
(d) none
Answer:
(c) both (a) and (b)

Question 51.
If the two colliding bodies stick together after collision such collisions are
(a) elastic collision
(b) inelastic collision
(c) perfectly inelastic collision
(d) head on collision
Answer:
(c) perfectly inelastic collision

Question 52.
When bubblegum is thrown on a moving vehicle, it sticks is an example for
(a) elastic collision
(b) inelastic collision
(c) perfectly inelastic collision
(d) none
Answer:
(c) perfectly inelastic collision

Question 53.
Elastic collision is due to
(a) conservative force
(b) non conservative force
(c) gravitational force
(d) electrostatic force
Answer:
(b) non conservative force

Question 54.
Inelastic collision is due to
(a) conservative force
(b) non conservative force
(c) gravitational force
(d) electrostatic force
Answer:
(b) non conservative force

Question 55.
If the velocity of separation is equal to the velocity of approach, then the collision is
(a) conservative force
(b) non conservative force
(c) gravitational force
(d) electrostatic force
Answer:
(a) conservative force

Question 56.
For elastic collision, coefficient of restitution is
(a) 0
(b) 1
(c) 0 < e < 1
(d) ∞
Answer:
(b) 1

Question 57.
For inelastic collision co-efficient of restitution is
(a) 0
(b) 1
(c) 0 < e < 1
(d) ∞
Answer:
(c) 0 < e < 1

Question 58.
For perfectly inelastic collision, coefficient of restitution is
(a) 0
(b) 1
(c) 0 < e < 1
(d) ∞
Answer:
(a) 0

Question 59.
The ratio of velocities of equal masses in an inelastic collision with one of the masses is stationary is
60. A box is dragged across a surface by a rope which makes an angle 45° with the horizontal. The tension in the rope is 100 N when the box is dragged 10 m. The work done is

Answer:
(a) \(\frac{1-e}{1+e}\)

Question 60.
A box is dragged across a surface by a rope which makes an angle 45° with the horizontal. The
tension in the rope is 100 N when the box is dragged 10 m. The work done is
(a) 707.1 J
(b) 607.1 J
(c) 1414.2 J
(d) 900 J
Answer:
(a) 707.1 J
Solution:
The component of force acting along the surface is T cos θ

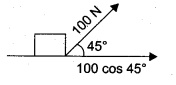
∴ Work done = T cos θ × x
= 10o cos 45° × 10
= 707.1 J

Question 61.
A position dependent force F = (7 – 2x + 3x²) N acts on a small body of mass 2 kg and displaces it from x = 0 to x = 5 m. Work done is
(a) 35 J
(b) 70 J
(c) 135 J
(d) 270 J
Answer:
(c) 135 J
Solution:

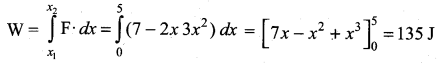
Question 62.
In gravitational field, the work done in moving a body from one point into another depends on
(a) initial and final positions
(b) distance between them
(c) actual distance covered
(d) velocity of motion
Answer:
(c) initial and final positions

Question 63.
A particle of mass “m” moving with velocity v strikes a particle of mass “2m” at rest and sticks to it. The speed of the combined mass is

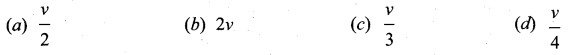
Answer:
(c) \(\frac{v}{3}\)
Solution:
According to conservation of linear momentum

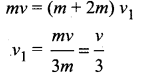
Question 64.
A force of (\(10 \hat{i}-3 \hat{j}+6 \hat{k}\)) N acts on a body of 5 kg and displaces it from (\(6 \hat{i}+5 \hat{j}-3 \hat{k}\)) to (\(10 \hat{i}-2 \hat{j}+7 k\)) m. The work done is
(a) 100 J
(b) 0
(c) 121 J
(d) none of these
Answer:
(c) 121 J
Solution:

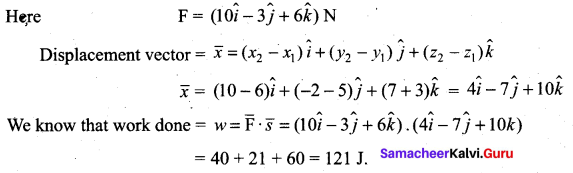
Question 65.
A 9 kg mass and 4 kg mass are moving with equal kinetic energies. The ratio of their momentum is
(a) 1 : 1
(b) 3 : 2
(c) 2 : 3
(d) 9 : 4.
Answer:
(b) 3 : 2
Solution:
Given that K.E are equal

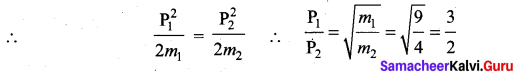
Question 66.
If momentum of a body increases by 25% its kinetic energy will increase by
(a) 25%
(b) 50%
(c) 125%
(d) 56.25%
Answer:
(d) 56.25%
Solution:
Let momentum of p₁ = 100% momentum of p₂ = 125%.

Question 67.
A missile fired from a launcher explodes in mid air, its total
(a) kinetic energy increases
(b) momentum increases
(c) kinetic energy decreases
(d) momentum decreases
Answer:
(a) kinetic energy increases

Question 68.
A bullet hits and gets embedded in a wooden block resting on a horizontal friction less surface. Which of the following is conserved?
(a) momentum alone
(b) kinetic energy alone
(c) both momentum and kinetic energy
(d) no quantity is conserved
Answer:
(a) momentum alone

Question 69.
Two balls of equal masses moving with velocities 10 m/s and -7 m/s respectively collide elastically. Their velocities after collision will be
(a) 3 ms^-1 and 17 ms^-1
(b) -7 ms^-1 and 10 ms^-1
(c) 10 ms^-1 and -7 ms^-1
(d) 3 ms^-1 and -70 ms^-1
Answer:
(b) -7 ms^-1 and 10 ms^-1

Question 70.
A spring of negligible mass having a force constant of 10 Nm^-1 is compressed by a force to a distance of 4 cm. A block of mass 900 g is free to leave the top of the spring. If the spring is released, the speed of the block is
(a) 11.3 ms^-1
(b) 13.3 × 101 ms^-1
(c) 13.3 × 10^-2 ms^-1
(d) 13.3 × 10^-3 ms^-1
Answer:
(c) 13.3 × 10^-2 ms^-1
Solution:
We know that, the potential energy of the spring = \(\frac{1}{2}\)kx². Here the potential energy of the spring is converted into kinetic energy of the block.

Question 71.
A particle falls from a height ftona fixed horizontal plate and rebounds. If e is the coefficient ” of restitution, the total distance travelled by the particle on rebounding when it stops is

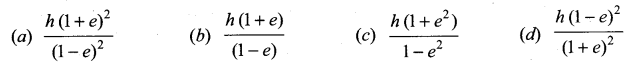
Answer:

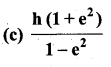
S = h + 2e²h + 2e⁴h + 2e⁶h + …..
S = h + 2h (e² + e⁴ + e⁶ +…)
By using binomixal expansion we can write it as

Question 72.
If the force F acting on a body as a function of x then the work done in moving a body from x = 1 m to x = 3m is

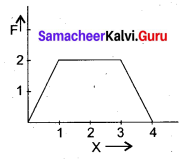
(a) 6 J
(b) 4 J
(c) 2.5 J
(d) 1 J
Answer:
(b) 4 J

Question 73.
A boy “A” of mass 50 kg climbs up a staircase in 10 s. Another boy “B” of mass 60 kg climbs up a Same staircase in 15s. The ratio of the power developed by the boys “A” and “B” is

Answer:
(a) \(\frac{5}{4}\)
Solution:

Samacheer Kalvi 11th Physics Short Answer Questions

Question 1.
Define work, energy, power.
Answer:
Work: Work is said to be done by the force when the force applied on a body displaces it.
Energy: Energy is defined as the ability to do work.
Power: The rate of work done is called power.

Question 2.
Discuss the possibilities of work done to be zero.
Answer:
Work done is zero in the following cases.
(i) When the force is zero (F = 0). For example, ,a body moving on a horizontal smooth frictionless surface will continue to do so as no force (not even friction) is acting along the plane. (This is an ideal situation.)
(ii) When the displacement is zero (dr = 0). For example, when force is applied on a rigid wall it does not produce any displacement. Hence, the work done is zero as shown in figure.
(iii) When the force and displacement are perpendicular (0 = 90°) to each other, when a body moves on a horizontal direction, the gravitational force (mg) does not work on the body, since it acts at right angles to the displacement as shown in Figure (b). In circular motion the centripetal force does not do work on the object moving on a circle as it is always perpendicular to the displacement as shown in Figure (c).

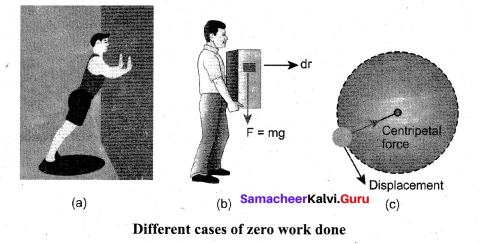
Question 3.
Derive the relation between momentum and kinetic energy.
Answer:
Consider an object of mass m moving with a velocity v. Then its linear momentum is


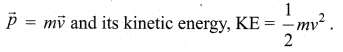
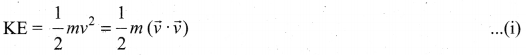
Multiplying both the numerator and denominator of equation (i) by mass m

where | \(\vec{p}\) | is the magnitude of the momentum. The magnitude of the linear momentum can be obtained by

Note that if kinetic energy and mass are given, only the magnitude of the momentum can be calculated but not the direction of momentum. It is because the kinetic energy and mass are scalars.

Question 4.
How can an object move with zero acceleration (constant velocity) when the external force is acting on the object?
Answer:
It is possible when there is another force which acts exactly opposite to the external applied force. They both cancel each other and the resulting net force becomes zero, hence the object moves with zero acceleration.

Question 5.
Why should the object be moved at constant velocity when we define potential energy?
Answer:
If the object does not move at constant velocity, then it will have different velocities at the initial and final locations. According to work-kinetic energy theorem, the external force will impart some extra kinetic energy. But we associate potential energy to the forces like gravitational force, spring force and coulomb force. So the external agency should not impart any kinetic energy when the object is taken from initial to final location.

Question 6.
Derive an expression for potential energy near the surface of the earth.
Answer:
The gravitational potential energy (U) at some height h is equal to the amount of work required to take the object from ground to that height h with constant velocity. Let us consider a body of mass m being moved from ground to the height h against the gravitational force as shown.

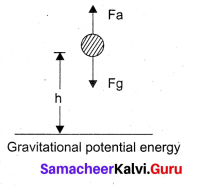
The gravitational force \(\overrightarrow{\mathrm{F}}_{g}\) acting on the body is, \(\overrightarrow{\mathrm{F}}_{g}=-m g \hat{j}\) (as Gravitational potential energy the force is in y direction, unit vector \(\hat{j}\) is used). Here, negative sign implies that the force is acting vertically downwards. In order to move the body without acceleration (or with constant velocity), an external applied force \(\overrightarrow{\mathrm{F}}_{a}\), equal in magnitude but opposite to that of gravitational force \(\overrightarrow{\mathrm{F}}_{g}\) has to be applied on the body i.e., \(\overrightarrow{\mathrm{F}}_{a}=-\overrightarrow{\mathrm{F}}_{g}\).
This implies that \(\overrightarrow{\mathrm{F}}_{a}=+m g \hat{j}\). The positive sign implies that the applied force is in vertically upward direction. Hence, when the body is lifted up its velocity remains unchanged and thus its kinetic energy also remains constant.
The gravitational potential energy (U) at some height h is equal to the amount of work required to take the object from the ground to that height h.

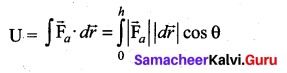
Since the displacement and the applied force are in the same upward direction, the angle between them, θ = 0°. Hence, cos 0° = 1 and | \(\overrightarrow{\mathrm{F}}_{a}\) | = mg and | \(d \vec{r}\) | = dr.

Question 7.
Explain force displacement graph for a spring.
Answer:

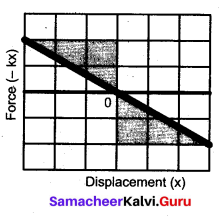
Since the restoring spring force and displacement are linearly related as F = – kx, and are opposite in direction, the graph between F and x is a straight line with dwelling only in the second and fourth quadrant as shown in Figure. The elastic potential energy can be easily calculated by drawing a F – x graph. The shaded area (triangle) is the work done by the spring force.

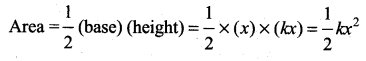
Question 8.
Explain the potential energy – displacement graph for a spring.
Answer:
A compressed or extended spring will transfer its stored potential energy into kinetic energy of the mass attached to the spring. The potential energy-displacement graph is shown in Figure.

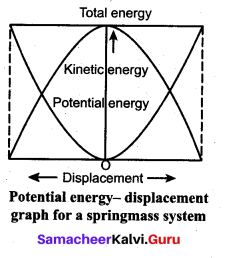
In a frictionless environment, the energy gets transferred from kinetic to potential and potential to kinetic repeatedly such that the total energy of the system remains constant. At the mean position,
∆KE = ∆U

Question 9.
Define unit of power.
Answer:
The unit of power is watt. One watt is defined as the power when one joule of work is done in one second.

Question 10.
Define average power and instantaneous power.
Answer:
The average power is defined as the ratio of the total work done to the total time taken.
P_av = total work done/total time taken The instantaneous power is defined as the power delivered at an instant
p_inst = dw/dt

Question 11.
Define elastic and inelastic collision.
Answer:
In any collision, if the total kinetic energy of the bodies before collision is equal to the total final kinetic energy of the bodies after collision then it is called as elastic collision.
In a collision the total initial kinetic energy of the bodies before collision is not equal to the . total final kinetic energy of the bodies after collision. Then it is called as inelastic collision.

Question 12.
What will happen to the potential energy of the system.
If (i) Two same charged particles are brought towards each other
(ii) Two oppositely charged particles are brought towards each other.
Answer:
(i) When the same charged particles are brought towards each other, the potential energy of the system will increase. Because work has to be done against the force of repulsion. This work done only stored as potential energy.
(ii) When two oppositely charged particles are brought towards each other, the potential energy of the system will decrease. Because work is done by the force of attraction between the charged particles.

Question 13.
Define the conservative and non-conservative forces. Give examples of each.
Answer:
Conservative force : e.g., Gravitational force, electrostatic force.
Non-Conservative force : e.g., forces of friction, viscosity.

Question 14.
A light body and a heavy body have same linear momentum. Which one has greater K.E ?
Answer:
Lighter body has more K.E. as K.E. = \(\frac{p^{2}}{2 m}\) and for constant p, K.E. \(\propto \frac{1}{m}\)

Question 15.
The momentum of the body is doubled, what % does its K.E change?
Answer:

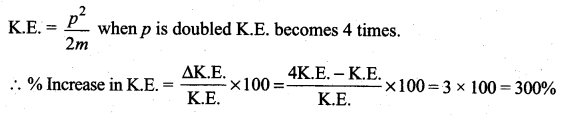
Question 16.
A body is moving along a circular path. How much work is done by the centripetal force?
Answer:
W = FS cos 90° = 0.

Question 17.
Which spring has greater value of spring constant – a hard spring or a delicate spring?
Answer:
Hard spring.

Question 18.
Two bodies stick together after collision. What type of collision is in between these two bodies? .
Answer:
Inelastic collision.

Question 19.
State the two conditions under which a force does not work.
Answer:

1. Displacement is zero or it is perpendicular to force.
2. Conservative force moves a body over a closed path.

Question 20.
How will the momentum of a body changes if its K.E. is doubled?
Answer:
Momentum becomes \(\sqrt{2}\) times.

Question 21.
K.E. of a body is increased by 300 %. Find the % increase in its momentum.
Answer:

Question 22.
A light and a heavy body have same K.E., which of the two have more momentum and why?
Answer:
Heavier body.

Question 23.
Does the P.E. of a spring decreases or increases when it is compressed or stretched?
Answer:
Increases because W.D. on it when it increases is compressed or stretched.

Question 24.
Name a process in which momentum changes but K.E. does not.
Answer:
Uniform circular motion.

Question 25.
What happens to the P.E. of a bubble when it rises in water?
Answer:
Decreases.

Question 26.
A body is moving at constant speed over a frictionless surface. What is the work done by the weight of the body?
Answer:
W = 0.

Question 27.
Define spring constant of a spring.
Answer:
It is the restoring force set up in a string per unit extension.

Samacheer Kalvi 11th Physics Short Answer Questions 2 Marks

Question 28.
How much work is done by a coolie walking on a horizontal platform with a load on his head? Explain.
Answer:
W = 0 as his displacement is along the horizontal direction and in order to balance the load on his head, he applies a force on it in the upward direction equal to its weight. Thus angle between force and displacement is zero.

Question 29.
Mountain roads rarely go straight up the slope, but wind up gradually. Why?
Answer:
If roads go straight up then angle of slope 0 would be large so frictional force f = µ mg cos θ would be less and the vehicles may slip. Also greater power would be required.

Question 30.
A truck and a car moving with the same K.E. on a straight road. Their engines are simultaneously switched off which one will stop at a lesser distance?
Answer:
By Work – Energy Theorem,
Loss in K.E. = W.D. against the force × distance of friction

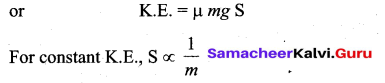
∴ Truck will stop in a lesser distance because of greater mass.

Question 31.
Is it necessary that work done in the motion of a body over a closed loop is zero for every force in nature? Why?
Answer:
No. W.D. is zero only in case of a conservative force.

Question 32.
How high must a body be lifted to gain an amount of P.E. equal to the K.E. it has when moving at speed 20 ms^-1. (The value of acceleration due to gravity at a place is 9.8 ms^-2).
Answer:

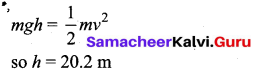
Question 33.
Give an example in which a force does work on a body but fails to change its K.E.
Answer:
When a body is pulled on a rough, horizontal surface with constant velocity. Work is done on the body but K.E. remains unchanged.

Question 34.
A bob is pulled sideway so that string becomes parallel to horizontal and released. Length of the pendulum is 2 m. If due to air resistance loss of energy is 10%, what is the speed with which the bob arrived at the lowest point.
Answer:

Question 35.
Two springs A and B are identical except that A is harder than B (K_A > K_B) if these are stretched by the equal force. In which spring will more work be done?
Answer:

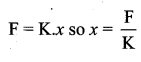
Question 36.
Find the work done if a particle moves from position r₁ = to a position \((3 \hat{i}+2 \hat{j}-6 \hat{k})\) to a position \(\vec{r}_{2}=(14 \hat{i}+13 \hat{j}-9 \hat{k})\) under the effect of force \(\overrightarrow{\mathrm{F}}=(4 \hat{i}+\hat{j}+3 \hat{k}) \mathrm{N}\)
Answer:

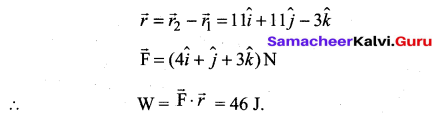
Question 37.
Spring A and B are identical except that A is stiffer than B, i.e., force constant k_A > k_B. In which spring is more work expended if they are stretched by the same amount?
Answer:

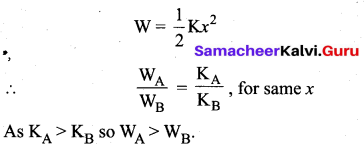
Question 38.
A ball at rest is dropped from a height of 12 m. It loses 25% of its kinetic energy in striking the ground, find the height to which it bounces. How do you account for the loss in kinetic energy?
Answer:
If ball bounces to height h’, then
mgh’ = 75% of mgh
∴ h’ = 0.75 h = 9 m.

Question 39.
Which of the two kilowatt hour or electron volt is a bigger unit of energy and by what factor?
Answer:
kwh is a bigger unit of energy.

Question 40.
A spring of force constant K is cut into two equal pieces. Calculate force constant of each part.
Answer:
Force constant of each half becomes twice the force constant of the original spring.

Samacheer Kalvi 11th Physics Short Answer Questions 3 Marks

Question 41.
A car of mass 2000 kg is lifted up a distance of 30 m by a crane in 1 min. A second crane does the same job in 2 min. Do the cranes consume the same or different amounts of fuel? What is the power supplied by each crane? Neglect Power dissipation against friction.
Answer:
t₁ = 1 min = 60 s, t₂ = 2 min = 120 s
W = Fs = mgs = 5.88 × 105 J
As both cranes do same amount of work so both consume same amount of fuel.

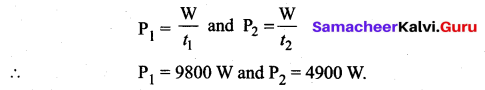
Question 42.
20 J work is required to stretch a spring through 0.1m. Find the force constant of the spring. If the spring is further stretched through 0.1 m, calculate work done.
Answer:
P.E. of spring when stretched through a distance 01m,

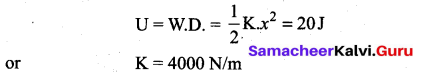
when spring is further stretched through 01m, then P.E. will be :

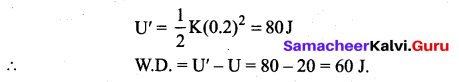
Question 43.
A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m³ in 15 min. If the tank is 40 m above the ground, how much electric power is consumed by the pump. The efficiency of the pump is 30%.
Answer:

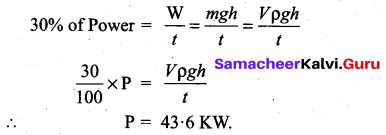
Question 44.
A ball bounces to 80% of its original height. Calculate the mechanical energy lost in each bounce.
Answer:
Let Initial P.E. = mgh
P.E. after first bounce = mg × 80% of h = 0.80 mgh
P.E. lost in each bounce = 0.20 mgh

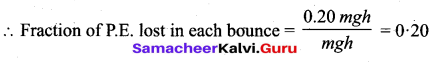
Samacheer Kalvi 11th Physics Long Answer Questions

Question 1.
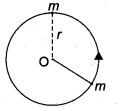
Obtain an expression for the critical vertical of a body revolving in a vertical circle
Answer:
Imagine that a body of mass (m) attached to one end of a massless and inextensible string executes circular motion in a vertical plane with the other end of the string fixed. The length of the string becomes the radius (r) of the circular path (See figure).

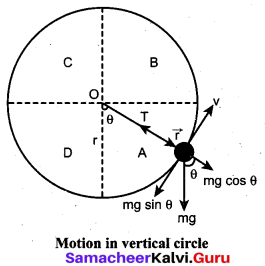
Let us discuss the motion of the body by taking the free body diagram (FBD) at a position where the position vector (\(\vec{r}\)) makes an angle θ with the vertically downward direction and the instantaneous velocity is as shown in Figure.
There are two forces acting on the mass.
1. Gravitational force which acts downward
2. Tension along the string.
Applying Newton’s second law on the mass, in the tangential direction,

The circle can be divided into four sections A, B, C, D for better understanding of the motion. The four important facts to be understood from the two equations are as follows:
(i) The mass is having tangential acceleration (g sin θ) for all values of θ (except θ = 0°), it is clear that this vertical circular motion is not a uniform circular motion.
(ii) From the equations (ii) and (i) it is understood that as the magnitude of velocity is not a constant in the course of motion, the tension in the string is also not constant.

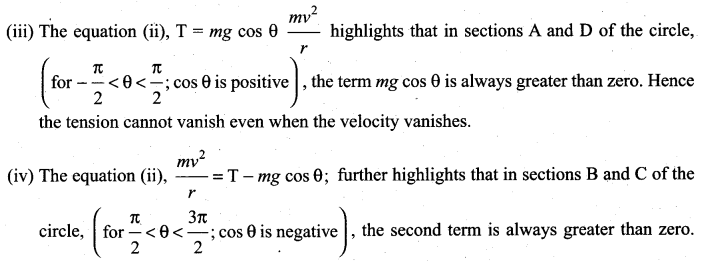
Hence velocity cannot vanish, even when the tension vanishes.
These points are to be kept in mind while solving problems related to motion in vertical circle.
To start with let us consider only two positions, say the lowest point 1 and the highest point 2 as shown in Figure for further analysis. Let the velocity of the body at the lowest point 1 be \(\vec{v}_{1}\), at the highest point 2 be \(\vec{v}_{2}\) and \(\vec{v}\) at any other point. The direction of velocity is tangential to the circular path at all points. Let \(\overrightarrow{\mathrm{T}}_{1}\) be the tension in the string at the lowest point and \(\overrightarrow{\mathrm{T}}_{2}\) be , the tension at the highest point and \(\overrightarrow{\mathrm{T}}\) be the tension at any other point. Tension at each point acts towards the center. The tensions and velocities at these two points can be found by applying the law of conservation of energy.

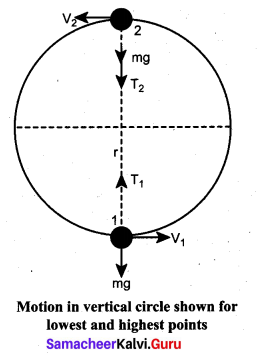
For the lowest point (1)
When the body is at the lowest point 1, the gravitational force \(m \vec{g}\) which acts on the body (vertically downwards) and another one is the tension \(\overrightarrow{\mathrm{T}}_{1}\), acting vertically upwards, i.e. towards the center. From the equation (ii), we get

For the highest point (2)
At the highest point 2, both the gravitational force mg on the body and the tension T₂ act downwards, i.e. towards the center again.

From equations (iv) and (ii), it is understood that T₁ > T₂. The difference in tension T₁ – T₂ is obtained by subtracting equation (iv) from equation (ii).

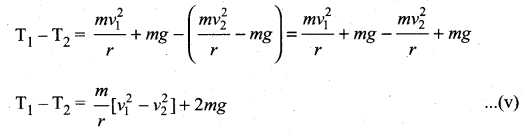
The term can be found easily by applying law of conservation of energy at point 1 and also at point 2.
Note: The tension will not do any work on the mass as the tension and the direction of motion is always perpendicular.
The gravitational force is doing work on the mass, as it is a conservative force the total energy of the mass is conserved throughout the motion.
Total energy at point 1 (E₁) is same as the total energy at a point 2 (E₂)
E₁ = E₂
Potential energy at point 1, U₁ = 0 (by taking reference as point 1)

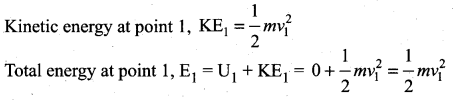
Similarly, Potential energy at point 2, U₂ = mg (2r) (h is 2r from point 1)

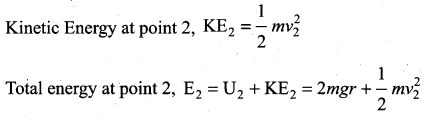
From the law of conservation of energy given in equation (vi), we get


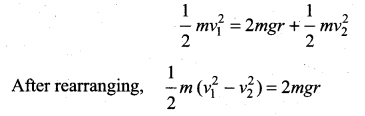
Substituting equation (vii) in equation (iv) we get,

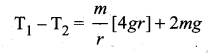
Therefore, the difference in tension is
T₁ – T₂ = 6 mg …(viii)
Minimum speed at the highest point (2)
The body must have a minimum speed at point 2 otherwise, the string will slack before reaching point 2 and the body will not loop the circle. To find this minimum speed let us take the tension T₂ = 0 in equation (iv).

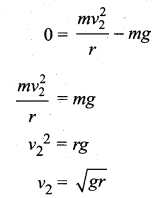
The body must have a speed at point 2, \(v_{2} \geq \sqrt{g r}\) to stay in the circular path.
Maximum speed at the lowest point 1
To have this minimum speed (\(v_{2}=\sqrt{g r}\)) at point 2, the body must have minimum speed also at point 1.
By making use of equation (vii) we can find the minimum speed at point 1.

Substituting equation (ix) in (vii),

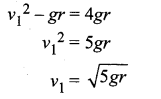
The body must have a speed at point 1, \(v_{1} \geq \sqrt{5 g r}\) to stay in the circular path.
From equations (ix) and (x), it is clear that the minimum speed at the lowest point 1 should be v 5 times more than the minimum speed at the highest point 2, so that the body loops without leaving the circle.

Question 2.
Obtain the expressions for the velocities of the two bodies after collision in the case of one dimensional elastic collision and discuss the special cases.
Answer:
Consider two elastic bodies of masses m₁ and m₂ moving in a straight line (along positive x direction) on a frictionless horizontal surface as shown in figure.

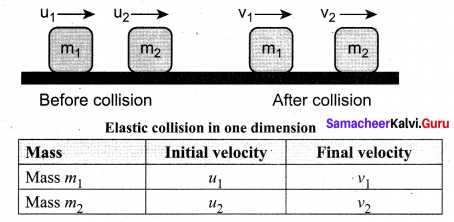
In order to have collision, we assume that the mass m₁ moves faster than mass m₂ i.e., u₁ > u₂.
For elastic collision, the total linear momentum and kinetic energies of the two bodies before and after collision must remain the same

From the law of conservation of linear momentum,
Total momentum before collision (p_i) = Total momentum after collision (p_f)

For elastic collision,
Total kinetic energy before collision KE_i = Total kinetic energy after collision KF_f

After simplifying and rearranging the terms,

Using the formula a² – b² = (a + b) (a – b), we can rewrite the above equation as
m₁(u₁ + v₁)(u₁ – v₁) = m₂ (v₂ + u₂) (v₂ – u₂) …(iv)
Dividing equation (iv) by (ii) gives,

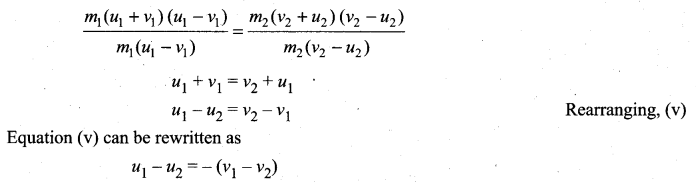
This means that for any elastic head on collision, the relative speed of the two elastic bodies after the collision has the same magnitude as before collision but in opposite direction. Further note that this result is independent of mass.
Rewriting the above equation for V₁ and v₂,
v₁ = v₂ + u₂ – u₁
Or v₂ = u₁ + v₁ – u₁
To find the final velocities v₁ and v₂ :
Substituting equation (vii) in equation (ii) gives the velocity of m₁ as
m₁ (u₁ – v₁ ) = m₂ (u₁ + v₁ – u₂ – u₂)
m₁u₁ – m₁v₁ = m₂(u₁ + v₁ – 2u₂)
m₁u₁ + 2m₂u₂ = m₁v₁ + m₂v₁

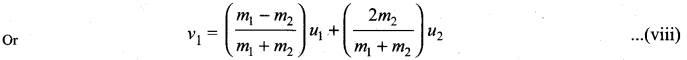
Similarly, by substituting (vi) in equation (ii) or substituting equation (viii) in equation (vii), we get the final velocity of m₂ as

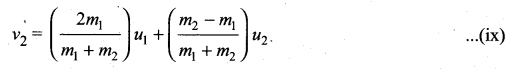
Case 1: When bodies has the same mass i.e., m₁ = m₂,

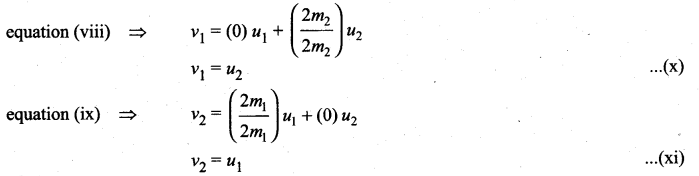
The equations (x) and (xi) show that in one dimensional elastic collision, when two bodies of equal mass collide after the collision their velocities are exchanged.
Case 2: When bodies have the same mass i.e., m₁ = m₂ and second body (usually called target) is at rest (u₂ = 0),
By substituting m₁m₂ = and u₂ = 0 in equations (viii) and equations (ix) we get, from equation
(viii) ⇒ V₁ = 0 …(xii)
from equation (ix) ⇒ v₂ = u₁ … (xiii)
Equations (xii) and (xiii) show that when the first body comes to rest the second body moves with the initial velocity of the first body.
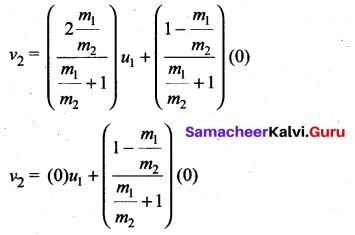
Case 3: The first body is very much lighter than the second body

Similarly, Dividing numerator and denominator of equation (ix) by m₂, we get

v₂ = 0
The equation (xiv) implies that the first body which is lighter returns back (rebounds) in the opposite direction with the same initial velocity as it has a negative sign. The equation (xv) implies that the second body which is heavier in mass continues to remain at rest even after collision. For example, if a ball is thrown at a fixed wall, the ball will bounce back from the wall with the same velocity with which it was thrown but in opposite direction.

Similarly,
Dividing numerator and denominator of equation (xiii) by m₁, we get

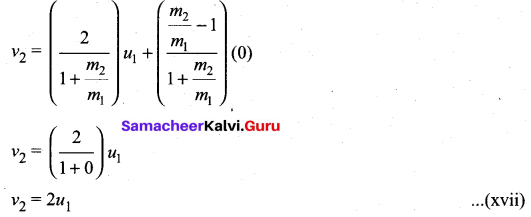
The equation (xvi) implies that the first body which is heavier continues to move with the same initial velocity. The equation (xvii) suggests that the second body which is lighter will move with twice the initial velocity of the first body. It means that the lighter body is thrown away from the point of collision.

Samacheer Kalvi 11th Physics Numerical Questions

Question 1.
A body is moving along z-axis of a coordinate system under the effect of a constant force F = Find the work done by the force in moving the body a distance of 2 m along z-axis.
Answer:

\(\mathrm{W}=\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{S}}=2 \mathrm{J}\)

Question 2.
Water is pumped out of a well 10 m deep by means of a pump rated 10 KW. Find the efficiency of the motor if 4200 kg of water is pumped out every minute. Take g = 10 m/s2.
Answer:

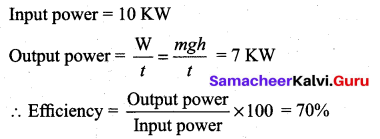
Question 3.
A railway carriage of mass 9000 kg moving with a speed of 36 kmph collides with a stationary carriage of same mass. After the collision, the carriages get coupled and move together. What is their common speed after collision? What type of collision is this?
Answer:
m₁ = 9000 kg, u₁ = 36 km/h = 10 m/s
m₂ = 9000 kg, u₂ = 0, v = v₁ = v₂ = ?
By conservation of momentum:
m₁u₁ + m₂u₂ = (m₁ + m₂)v
∴ v = 5 m/s

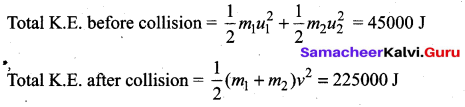
As total K.E. after collision < Total K.E. before collision
∴ collision is inelastic

Question 4.
In lifting a 10 kg weight to a height of 2m, 230 J energy is spent. Calculate the acceleration with which it was raised.
Answer:
W = mgh + mah = m(g + a)h
∴ a = 1.5 m/s².

Question 5.
A bullet of mass 0.02 kg is moving with a speed of 10 ms^-1. It can penetrate 10 cm of a wooden block, and comes to rest. If the thickness of the target would be 6 cm only, find the K.E. of the bullet when it comes out.

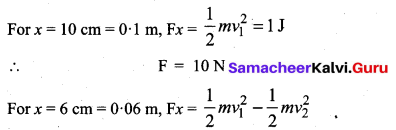
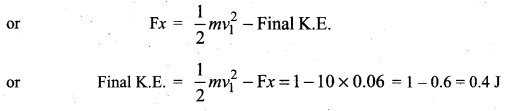
Question 6.
A man pulls a lawn roller through a distance of 20 m with a force of 20 kg weight. If he applies the force at an angle of 60° with the ground, calculate the power developed if he takes 1 min in doing so.
Answer:

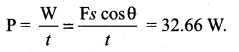
Question 7.
A body of mass 0.3 kg is taken up an inclined plane to length 10 m and height 5 m and then allowed to slide down to the bottom again. The coefficient of friction between the body and the plane is 0.15. What is the
(i) work done by the gravitational force over the round trip?
(ii) work done by the applied force over the upward journey?
(iii) work done by frictional force over the round trip?
(iv) kinetic energy of the body at the end of the trip?
How is the answer to (iv) related to the first three answers?
Answer:


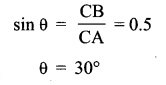
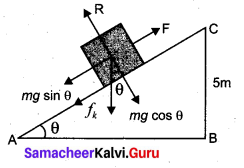
(i) W = FS = – mg sin θ × h = -14.7 J is the W.D. by gravitational force in moving plane.
W’ = FS = + mg sin θ × h = 14.7 J is the W.D. by gravitational force in moving the body down the inclined plane.
∴ Total W.D. round the trip, W₁ = W + W’ = 0
(ii) Force needed to move the body up the inclined plane,
F = mg sin θ + f_k = mg sin θ + µ_kR = mg sin θ + µ_k mg cos θ
∴ W.D. by force over the upward journey is
W₂ = F × l = mg (sin θ + µ_k cos θ)l = 18.5 J
(iii) W.D. by frictional force over the round trip,
W₃ = -fk(l + l) = -2fkl = -2µ_kcos θ l = -7.6 J
(iv) K.E. of the body at the end of round trip
= W.D. by net force in moving the body down the inclined plane
= (mg sin θ – µ_kcos θ) l
= 10.9 J
⇒ K.E. of body = net W.D. on the body.

Question 8.
Two identical 5 kg blocks are moving with same speed of 2 ms^-1 towards each other along a frictionless horizontal surface. The two blocks collide, stick together and come to rest. Consider the two blocks as a system. Calculate work done by
(i) external forces and
(ii) Internal forces.
Answer:
Here no external forces are acting on the system so :
\(\overrightarrow{\mathrm{F}}_{\mathrm{ext}}=0 \Rightarrow \mathrm{W}_{\mathrm{ext}}=0\)
According to work-energy theorem :
Total W.D. = Change in K.E.
or W_ext + = Final K.E. – Initial K.E.

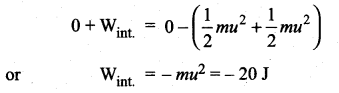
Question 9.
A truck of mass 1000 kg accelerates uniformly from rest to a velocity of 15 ms^-1 in 5 seconds. Calculate
(i) its acceleration,
(ii) its gain in K.E.,
(iii) average power of the engine during this period, neglect friction.
Answer:

Question 10.
An elevator which can carry a maximum load of 1800 kg (elevator + passengers) is moving up with a constant speed of 2 ms^-1. The frictional force opposing the motion is 4000 N. Determine the minimum power delivered by the motor to the elevator in watts as well as in horse power.
Answer:
Downward force on the elevator is :
F = mg + f = 22000 N
∴ Power supplied by motor to balance this force is :

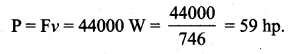
Question 11.
To simulate car accidents, auto manufacturers study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car of mass 1000 kg moving with a speed 18.0 kmh^-1 on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25 × 10^-3 Nm^-1. What is the maximum compression of the spring?
Answer:
At maximum compression x_m, the K.E. of the car is converted entirely into the P.E. of the spring.