Students can Download Physics Chapter 3 Laws of Motion Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Physics Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 3 Laws of Motion
Samacheer Kalvi 11th Physics Chapter 3 Laws of Motion Textual Questions Solved
Samacheer Kalvi 11th Physics Laws of Motion Multiple Choice Questions
Question 1.
When a car takes a sudden left turn in the curved road, passengers are pushed towards the right due to
(a) inertia of direction
(b) inertia of motion
(c) inertia of rest
(d) absence of inertia
Answer:
(a) inertia of direction
Question 2.
An object of mass m held against a vertical wall by applying horizontal force F as shown in the figure. The minimum value of the force F is [IIT JEE 1994]
(a) Less than mg
(b) Equal to mg
(c) Greater than mg
(d) Cannot determine
Answer:
(c) Greater than mg
Question 3.
A vehicle is moving along the positive x direction, if sudden brake is applied, then
(a) frictional force acting on the vehicle is along negative x direction
(b) frictional force acting on the vehicle is along positive x direction
(c) no frictional force acts on the vehicle
(d) frictional force acts in downward direction
Answer:
(a) frictional force acting on the vehicle is along negative x direction
![]()
The normal force formula is defined as the force that any surface exerts on any other object.
Question 4.
A book is at rest on the table which exerts a normal force on the book. If this force is considered as reaction force, what is the action force according to Newton’s third law?
(a) Gravitational force exerted by Earth on the book
(b) Gravitational force exerted by the book on Earth
(c) Normal force exerted by the book on the table
(d) None of the above
Answer:
(c) Normal force exerted by the book on the table
Question 5.
Two masses m1 and m2 are experiencing the same force where m1 < m2 The ratio of their acceleration \(\frac{a_{1}}{a_{2}}\) is –
(a) 1
(b) less than 1
(c) greater than 1
(d) all the three cases
Answer:
(c) greater than 1
Question 6.
Choose appropriate free body diagram for the particle experiencing net acceleration along negative y direction. (Each arrow mark represents the force acting on the system).

Answer:
Question 7.
A particle of mass m sliding on the smooth double inclined plane (shown in figure) will experience –
(a) greater acceleration along the path AB
(b) greater acceleration along the path AC
(c) same acceleration in both the paths
(d) no acceleration in both the paths
Answer:
(a) greater acceleration along the path AC
![]()
Question 8.
Two blocks of masses m and 2m are placed on a smooth horizontal surface as shown. In the first case only a force F1 is applied from the left. Later only a force F2 is applied from the right. If the force acting at the interface of the two blocks in the two cases is same, then F1 : F2 is [Physics Olympiad 2016]
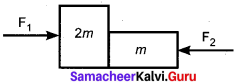
(a) 1 : 1
(b) 1 : 2
(c) 2 : 1
(d) 1 : 3
Answer:
(c) 2 : 1
Question 9.
Force acting on the particle moving with constant speed is –
(a) always zero
(b) need not be zero
(c) always non zero
(d) cannot be concluded
Answer:
(b) need not be zero
Question 10.
An object of mass m begins to move on the plane inclined at an angle 0. The coefficient of static friction of inclined surface is lay. The maximum static friction experienced by the mass is –
(a) mg
(b) µs mg
(c) µs mg sin θ
(d) µs mg cos θ
Answer:
(d) µs mg cos θ
Question 11.
When the object is moving at constant velocity on the rough surface –
(a) net force on the object is zero
(b) no force acts on the object
(c) only external force acts on the object
(d) only kinetic friction acts on the object
Answer:
(a) net force on the object is zero
Question 12.
When an object is at rest on the inclined rough surface –
(a) static and kinetic frictions acting on the object is zero
(b) static friction is zero but kinetic friction is not zero
(c) static friction is not zero and kinetic friction is zero
(d) static and kinetic frictions are not zero
Answer:
(c) static friction is not zero and kinetic friction is zero
![]()
Question 13.
The centrifugal force appears to exist –
(a) only in inertial frames
(b) only in rotating frames
(c) in any accelerated frame
(d) both in inertial and non-inertial frames
Answer:
(b) only in rotating frames
Question 14.
Choose the correct statement from the following –
(a) Centrifugal and centripetal forces are action reaction pairs
(b) Centripetal forces is a natural force
(c) Centrifugal force arises from gravitational force
(d) Centripetal force acts towards the center and centrifugal force appears to act away from the center in a circular motion
Answer:
(d) Centripetal force acts towards the center and centrifugal force appears to act away from the center in a circular motion
Question 15.
If a person moving from pole to equator, the centrifugal force acting on him –
(a) increases
(b) decreases
(c) remains the same
(d) increases and then decreases
Answer:
(a) increases
Samacheer Kalvi 11th Physics Laws of Motion Short Answer Questions
Question 1.
Explain the concept of inertia. Write two examples each for inertia of motion, inertia of rest and inertia of direction.
Answer:
The inability of objects to move on its own or change its state of motion is called inertia. Inertia means resistance to change its state. There are three types of inertia:
1. Inertia of rest:
The inability of an object to change its state of rest is called inertia of rest.
Example:
- When a stationary bus starts to move, the passengers experience a sudden backward push.
- A book lying on the table will remain at rest until it is moved by some external agencies.
2. Inertia of motion:
The inability of an object to change its state of uniform speed (constant speed) on its own is called inertia of motion.
Example:
- When the bus is in motion, and if the brake is applied suddenly, passengers move forward and hit against the front seat.
- An athlete running is a race will continue to run even after reaching the finishing point.
3. Inertia of direction:
The inability of an object to change its direction of motion on its own is called inertia of direction.
Example:
- When a stone attached to a string is in whirling motion, and if the string is cut suddenly, the stone will not continue to move in circular motion but moves tangential to the circle.
- When a bus moving along a straight line takes a turn to the right. The passengers are thrown towards left.
![]()
Question 2.
State Newton’s second law.
Answer:
The force acting on an object is equal to the rate of change of its momentum –
\(\overline{\mathrm{F}}\) = \(\frac{d \bar{p}}{d t}\)
Question 3.
Define one newton.
Answer:
One newton is defined as the force which acts on 1 kg of mass to give an acceleration 1 ms-2 in the direction of the force.
Question 4.
Show that impulse is the change of momentum.
Answer:
According to Newton’s Second Law
F = \(\frac {dp}{dt}\) i.e. dp = Fdt
Integrate it over a time interval from ti to tf

Pi → initial momentum of the object at ti
Pf → Final momentum of the object at tf
Pf – Pi = ∆p = change in momentum during the time interval ∆t.
\(\int_{t_{i}}^{t_{f}} \mathrm{F} \cdot d t=\mathrm{J}\) is called the impulse.
If the force is constant over the time interval ∆t, then
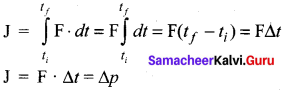
Hence the proof.
Question 5.
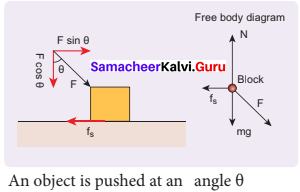
Using free body diagram, show that it is easy to pull an object than to push it.
Answer:
When a body is pushed at an arbitrary angle θ [0 to \(\frac {π}{2}\)], the applied force F can be resolved into two components as F sin 0 parallel to the surface and F cos 0 perpendicular to the surface as shown in figure. The total downward force acting on the body is mg + F cos θ. It implies that the normal force acting on the body increases. Since there is no acceleration along the vertical direction the normal force N is equal to
Npush = mg + F cos θ …………(1)
As a result the maximal static friction also increases and is equal to
\(f_{S}^{\max }\) = \(\mu_{r} \mathrm{N}_{\mathrm{push}}\) = µs(mg + F cos θ) ……(2)
Equation (2) shows that a greater force needs to be applied to push the object into motion.
When an object is pulled at an angle θ, the applied force is resolved into two components as shown in figure. The total downward force acting on the object is –
Npull = mg – F cos θ ………….(3)
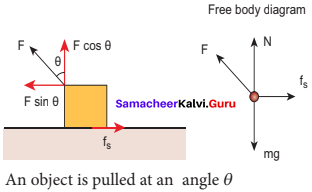
Equation (3) shows that the normal force is less than – Npush. From equations (1) and (3), it is easier to pull an object than to push to make it move.
![]()
Question 6.
Explain various types of friction. Suggest a few methods to reduce friction.
Answer:
There are two types of Friction:
(1) Static Friction:
Static friction is the force which opposes the initiation of motion of an object on the surface. The magnitude of static frictional force fs lies between
\(0 \leq f_{s} \leq \mu_{s} \mathrm{N}\)
where, µs – coefficient of static friction
N – Normal force
(2) Kinetic friction:
The frictional force exerted by the surface when an object slides is called as kinetic friction. Also called as sliding friction or dynamic friction,
fk – µkN
where µk – the coefficient of kinetic friction
N – Normal force exerted by the surface on the object
Methods to reduce friction:
Friction can be reduced
- By using lubricants
- By using Ball bearings
- By polishing
- By streamlining
Question 7.
What is the meaning by ‘pseudo force’?
Answer:
Pseudo force is an apparent force which has no origin. It arises due to the non-inertial nature of the frame considered.
Question 8.
State the empirical laws of static and kinetic friction.
Answer:
The empirical laws of friction are:
- Friction is independent of surface of contact.
- Coefficient of kinetic friction is less than coefficient of static friction.
- The direction of frictional force is always opposite to the motion of one body over the other.
- Frictional force always acts on the object parallel to the surface on which the objet is placed,
- The magnitude of frictional force between any two bodies in contact is directly proportional to the normal reaction between them.
Question 9.
State Newton’s third law.
Answer:
Newton’s third law states that for every action there is an equal and opposite reaction.
Question 10.
What are inertial frames?
Answer:
Inertial frame is the one in which if there is no force on the object, the object moves at constant velocity.
![]()
Question 11.
Under what condition will a car skid on a leveled circular road?
Answer:
On a leveled circular road, if the static friction is not able to provide enough centripetal ’force to turn, the vehicle will start to skid
\(\mu_{s}<\frac{v^{2}}{r g}\)
Samacheer Kalvi 11th Physics Laws of Motion Long Answer Questions
Question 1.
Prove the law of conservation of linear momentum. Use it to find the recoil velocity of a gun when a bullet is fired from it.
Answer:
In nature, conservation laws play a very important role. The dynamics of motion of bodies can be analysed very effectively using conservation laws. There are three conservation laws in mechanics. Conservation of total energy, conservation of total linear momentum, and conservation of angular momentum. By combining Newton’s second and third laws, we can derive the law of conservation of total linear momentum. When two particles interact with each other, they exert equal and opposite forces on each other.
The particle 1 exerts force \(\overrightarrow{\mathrm{F}}_{12}\) on particle 2 and particle 2 exerts an exactly equal and opposite force \(\overrightarrow{\mathrm{F}}_{12}\) on particle 1 according to Newton’s third law.
\(\overrightarrow{\mathrm{F}}_{12}\) = –\(\overrightarrow{\mathrm{F}}_{12}\) ……..(1)
In terms of momentum of particles, the force on each particle (Newton’s second law) can be written as –
\(\overrightarrow{\mathrm{F}}_{12}\) = \(\frac{d \vec{p}_{1}}{d t}\) and \(\overrightarrow{\mathrm{F}}_{21}\) = \(\frac{d \vec{p}_{2}}{d t}\) ………(2)
Here \(\vec{p}_{1}\) is the momentum of particle 1 which changes due to the force \(\overrightarrow{\mathrm{F}}_{12}\) exerted by particle 2. Further Po is the momentum of particle \(\vec{p}_{2}\) This changes due to \(\overrightarrow{\mathrm{F}}_{21}\) exerted by particle 1.
Substitute equation (2) in equation (1)
\(\frac{d \vec{p}_{1}}{d t}\) = – \(\frac{d \vec{p}_{2}}{d t}\) …………(3)
\(\frac{d \vec{p}_{1}}{d t}\) + \(\frac{d \vec{p}_{2}}{d t}\) = 0 ………(4)
\(\frac {d}{dt}\)(\(\vec{p}_{1}\) + \(\vec{p}_{2}\)) = 0
It implies that \(\vec{p}_{1}\) + \(\vec{p}_{2}\) = constant vector (always).
\(\vec{p}_{1}\) + \(\vec{p}_{2}\) is the total linear momentum of the two particles (\(\vec{p}_{tot}\) = \(\vec{p}_{1}\) + \(\vec{p}_{2}\)).It is also called as total linear momentum of the system. Here, the two particles constitute the system. From this result, the law of conservation of linear momentum can be stated as follows.
If there are no external forces acting on the system, then the total linear momentum of the system (\(\vec{p}_{tot}\)) is always a constant vector. In other words, the total linear momentum of the system is conserved in time. Here the word ‘conserve’ means that \(\vec{p}_{1}\) and \(\vec{p}_{2}\) can vary, in such a way that \(\vec{p}_{1}\) + \(\vec{p}_{2}\) is a constant vector.
The forces \(\overrightarrow{\mathrm{F}}_{12}\) and \(\overrightarrow{\mathrm{F}}_{21}\) are called the internal forces of the system, because they act only between the two particles. There is no external force acting on the two particles from outside. In such a case the total linear momentum of the system is a constant vector or is conserved.
Meaning of law of conservation of momentum:
1. The Law of conservation of linear momentum is a vector law. It implies that both the magnitude and direction of total linear momentum are constant. In some cases, this total momentum can also be zero.
2. To analyse the motion of a particle, we can either use Newton’s second law or the law of conservation of linear momentum. Newton’s second law requires us to specify the forces involved in the process. This is difficult to specify in real situations. But conservation of linear momentum does not require any force involved in the process. It is convenient and hence important.
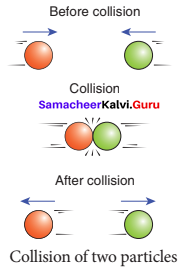
For example, when two particles collide, the forces exerted by these two particles on each other is difficult to specify. But it is easier to apply conservation of linear momentum during the collision process.
Examples:
Consider the firing of a gun. Here the system is Gun+bullet. Initially the gun and bullet are at rest, hence the total linear momentum of the system is zero. Let \(\vec{p}_{1}\) be the momentum of the bullet and \(\vec{p}_{2}\) the momentum of the gun before firing. Since initially both are at rest,
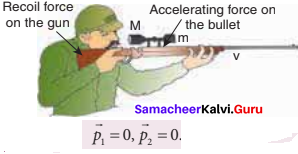
Total momentum before firing the gun is zero, \(\vec{p}_{1}\) + \(\vec{p}_{2}\) = 0.
According to the law of conservation of linear momentum, total linear momentum has to be zero after the firing also.
When the gun is fired, a force is exerted by the gun on the bullet in forward direction. Now the momentum of the bullet changes from \(\vec{p}_{1}\) to \(\vec{p}_{1}\) To conserve the total linear momentum of the system, the momentum of the gun must also change from \(\vec{p}_{2}\) to \(\vec{p}_{2}^{\prime}\). Due to the conservation of linear momentum, \(\vec{p}_{1}\) + \(\vec{p}_{2}^{\prime}\) = 0.
It implies that \(\vec{p}_{1}^{\prime}\)= \(\vec{p}_{2}^{\prime}\), the momentum of the gun is exactly equal, but in the opposite direction to the momentum of the bullet. This is the reason after firing, the gun suddenly moves backward with the momentum (-\(\vec{p}_{2}^{\prime}\)). It is called ‘recoil momentum’. Th is is an example of conservation of total linear momentum.
Question 2.
What are concurrent forces? State Lami’s theorem.
Answer:
Concurrent force:
A collection of forces is said to be concurrent, if the lines of forces act at a common point.
Lami’s Theorem:
If a system of three concurrent and coplanar forces is in equilibrium, then Lami’s theorem states that the magnitude of each force of the system is proportional to sine of the angle between the other two forces.
i.e. |\(\overrightarrow{\mathrm{F}}_{1}\)|∝ sin α, |\(\overrightarrow{\mathrm{F}}_{2}\)| ∝ sin β, |\(\overrightarrow{\mathrm{F}}_{2}\)| ∝ sin γ,
Question 3.
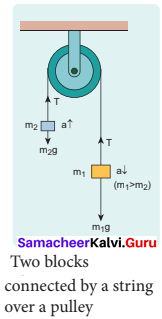
Explain the motion of blocks connected by a string in
- Vertical motion
- Horizontal motion.
Answer:
When objects are connected by strings and When objects are connected by strings and a force F is applied either vertically or horizontally or along an inclined plane, it produces a tension T in the string, which affects the acceleration to an extent. Let us discuss various cases for the same.
Case 1:
Vertical motion:
Consider two blocks of masses m1 and m2 (m1> m2) connected by a light and in-extensible string that passes over a pulley as shown in Figure.
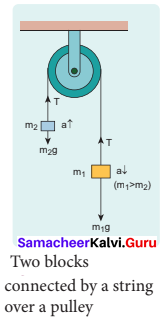
Let the tension in the string be T and acceleration a. When the system is released, both the blocks start moving, m2 vertically upward and mk, downward with same acceleration a. The gravitational force m1g on mass m1 is used in lifting the mass m2. The upward direction is chosen as y direction. The free body diagrams of both masses are shown in Figure.
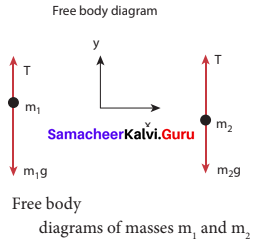
Applying Newton’s second law for mass m2 T \(\hat{j}\) – m2 g \(\hat{j}\) = m2 a \(\hat{j}\) The left hand side of the above equation is the total force that acts on m2 and the right hand side is the product of mass and acceleration of m2 in y direction.
By comparing the components on both sides, we get
T = m2 g = m2 a ……….(1)
Similarly, applying Newton’s second law for mass m2
T \(\hat{j}\) – m1 g\(\hat{j}\) = m1a\(\hat{j}\)
As mass m1 moves downward (-\(\hat{j}\)), its acceleration is along (-\(\hat{j}\))
By comparing the components on both sides, we get
T = m1g = -m1a
m1g – T = m1a ………..(2)
Adding equations (1) and (2), we get
m1g – m2g = m1a + m2a
(m1 – m2)g = (m1 + m2)a …………(3)
From equation (3), the acceleration of both the masses is –
a = (\(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\))g ………..(4)
If both the masses are equal (m1 = m2), from equation (4)
a = 0
This shows that if the masses are equal, there is no acceleration and the system as a whole will be at rest.
To find the tension acting on the string, substitute the acceleration from the equation (4) into the equation (1).
T = m2g = m2(\(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\))
T = m2g + m2 (\(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\))g ……….(5)
By taking m2g common in the RHS of equation (5)

Equation (4) gives only magnitude of acceleration.
For mass m1, the acceleration vector is given by \(\vec{a}\) = –\(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\)\(\hat{j}\)
For mass m2, the acceleration vector is given by \(\vec{a}\) = \(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\) \(\hat{j}\)
Case 2:
Horizontal motion:
In this case, mass m2 is kept on a horizontal table and mass m1, is hanging through a small pulley as shown in figure. Assume that there is no friction on the surface
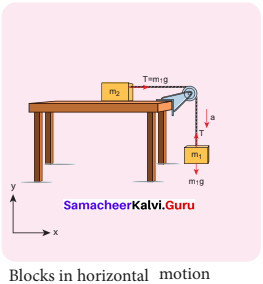
As both the blocks are connected to the un stretchable string, if m1 moves with an acceleration a downward then m2 also moves with the same acceleration a horizontally.
The forces acting on mass m2 are
- Downward gravitational force (m2g)
- Upward normal force (N) exerted by the surface
- Horizontal tension (T) exerted by the string
The forces acting on mass m1 are
- Downward gravitational force (m1g)
- Tension (T) acting upwards
The free body diagrams for both the masses is shown in figure.
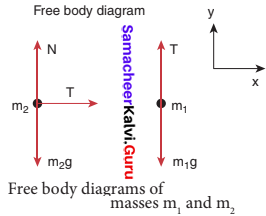
Applying Newton’s second law for m1
T\(\hat{i}\) – m1g\(\hat{j}\) = -m1a\(\hat{j}\) (alongy direction)
By comparing the components on both sides of the above equation,
T – m1g = -m1a …………(1)
Applying Newton’s second law for m2
Ti = m1ai (along x direction)
By comparing the components on both sides of above equation,
T = m2a ………….(2)
There is no acceleration along y direction for m2.
N\(\hat{j}\) – m2g\(\hat{j}\) = 0
By comparing the components on both sides of the above equation
N – m2g = 0
N = m2g ……….(3)
By substituting equation (2) in equation (1), we can find the tension T
m2a – m1g = -m1a
m2a + m1a = m1g
a = \(\frac{m_{1}}{m_{1}+m_{2}}\)g …………(4)
Tension in the string can be obtained by substituting equation (4) in equation (2)
T = \(\frac{m_{1} m_{2}}{m_{1}+m_{2}}\)g ………..(5)
Comparing motion in both cases, it is clear that the tension in the string for horizontal motion is half of the tension for vertical motion for same set of masses and strings. This result has an important application in industries. The ropes used in conveyor belts (horizontal motion) work for longer duration than those of cranes and lifts (vertical motion).
![]()
Question 4.
Briefly explain the origin of friction. Show that in an inclined plane, angle of friction is pqual to angle of repose.
Answer:
If a very gentle force in the horizontal direction is given to an object at rest on the table it does not move. It is because of the opposing force exerted by the surface on the object which resists its motion. This force is called the frictional force. During the time of Newton and Galileo, frictional force was considered as one of the natural forces like gravitational force. But in the twentieth century, the understanding on atoms, electron and protons has changed the perspective.
The frictional force is actually the electromagnetic force between the atoms on the two surfaces. Even well polished surfaces have irregularities on the surface at the microscopic level. The component of force parallel to the inclined plane (mg sin θ) tries to move the object down. The component of force perpendicular to the inclined plane (mg cos θ) is balanced by the Normal force (N).
N = mg cos θ ………(1)
When the object just begins to move, the static friction attains its maximum value
fs = \(f_{s}^{\max }\) = µs N
This friction also satisfies the relation
\(f_{s}^{\max }\) = µs mg sin θ ……….(2)
Equating the right hand side of equations (1) and (2),
(\(f_{s}^{\max }\))/N = sin θ / cos θ
From the definition of angle of friction, we also know that
tan θ = µs ………..(3)
in which θ is the angle of friction.
Thus the angle of repose is the same as angle of friction. But the difference is that the angle of repose refers to inclined surfaces and the angle of friction is applicable to any type of surface.
Question 5.
State Newton’s three laws and discuss their significance.
Answer:
First Law:
Every object continues to be in the state of rest or of uniform motion (constant velocity) unless there is external force acting on it.
Second Law:
The force acting on an object is equal to the rate of change of its momentum
Third Law:
For every action there is an equal and opposite reaction.
Significance of Newton’s Laws:
1. Newton’s laws are vector laws. The equation \(\overline{\mathrm{F}}\) = m\(\overline{\mathrm{a}}\) is a vector equation and essentially it is equal to three scalar equations. In Cartesian coordinates, this equation can be written as Fx\(\hat{i}\) + Fy\(\hat{j}\) + Fz\(\hat{j}\) = max\(\hat{i}\) + may\(\hat{j}\) + maz\(\hat{j}\)
By comparing both sides, the three scalar equations are
Fx = max The acceleration along the x-direction depends only on the component of force acting along the x – direction.
Fy = may The acceleration along the y direction depends only on the component of force acting along the y – direction.
Fz = maz The acceleration along the z direction depends only on the component of force acting along the z – direction.
From the above equations, we can infer that the force acting along y direction cannot alter the acceleration along x direction. In the same way, Fz cannot affect ay and ax. This understanding is essential for solving problems.
2. The acceleration experienced by the body at time t depends on the force which acts on the body at that instant of time. It does not depend on the force which acted on the body before the time t. This can be expressed as
\(\overline{\mathrm{F}}\)(t) = m\(\overline{\mathrm{a}}\)(t)
Acceleration of the object does not depend on the previous history of the force. For example, when a spin bowler or a fast bowler throws the ball to the batsman, once the ball leaves the hand of the bowler, it experiences only gravitational force and air frictional force. The acceleration of the ball is independent of how the ball was bowled (with a lower or a higher speed).
3. In general, the direction of a force may be different from the direction of motion. Though in some cases, the object may move in the same direction as the direction of the force, it is not always true. A few examples are given below.
Case 1:
Force and motion in the same direction:
When an apple falls towards the Earth, the direction of motion (direction of velocity) of the apple and that of force are in the same downward direction as shown in the Figure.
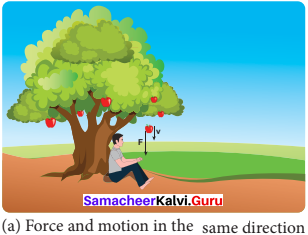
Case 2:
Force and motion not in the same direction:
The Moon experiences a force towards the Earth. But it actually moves in elliptical orbit. In this case, the direction of the force is different from the direction of motion as shown in Figure.
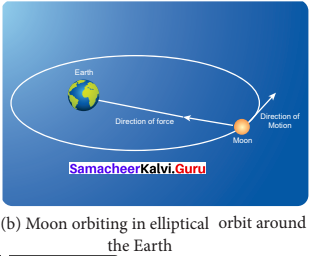
Case 3:
Force and motion in opposite direction:
If an object is thrown vertically upward, the direction of motion is upward, but gravitational force is downward as shown in the Figure.

Case 4:
Zero net force, but there is motion:
When a raindrop gets detached from the cloud it experiences both downward gravitational force and upward air drag force. As it descends towards the Earth, the upward air drag force increases and after a certain time, the upward air drag force cancels the downward gravity. From then on the raindrop moves at constant velocity till it touches the surface of the Earth. Hence the raindrop comes with zero net force, therefore with zero acceleration but with non-zero terminal velocity. It is shown in the Figure
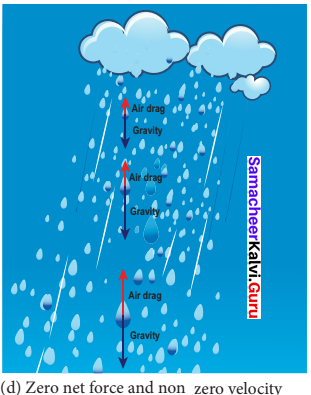
4. If multiple forces \(\overrightarrow{\mathrm{F}}_{1}\), \(\overrightarrow{\mathrm{F}}_{2}\), \(\overrightarrow{\mathrm{F}}_{3}\),……. \(\overrightarrow{\mathrm{F}}_{n}\) act on the same body, then the total force (\(\overrightarrow{\mathrm{F}}_{net}\)) is equivalent to the vectorial sum of the individual forces. Their net force provides the acceleration.
\(\overrightarrow{\mathrm{F}}_{net}\) = \(\overrightarrow{\mathrm{F}}_{1}\) + \(\overrightarrow{\mathrm{F}}_{2}\) + \(\overrightarrow{\mathrm{F}}_{3}\) + ……… + \(\overrightarrow{\mathrm{F}}_{n}\)
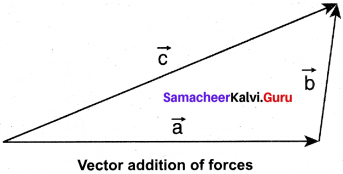
Newton’s second law for this case is –
\(\overrightarrow{\mathrm{F}}_{net}\) = m\(\overline{\mathrm{a}}\)
In this case the direction of acceleration is in the direction of net force.
Example:
Bow and arrow
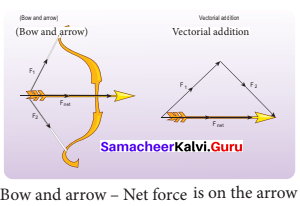
5. Newton’s second law can also be written in the following form.
Since the acceleration is the second derivative of position vector of the body \(\left(\vec{a}=\frac{d^{2} \vec{r}}{d t^{2}}\right)\)
the force on the body is –
\(\overline{\mathrm{F}}\) = m\(\frac{d^{2} \vec{r}}{d t^{2}}\)
From this expression, we can infer that Newton’s second law is basically a second order ordinary differential equation and whenever the second derivative of position vector is not zero, there must be a force acting on the body.
6. If no force acts on the body then Newton’s second law, m = \(\frac{d \vec{v}}{d t}\) = 0
It implies that \(\overline{\mathrm{v}}\) = constant. It is essentially Newton’s first law. It implies that the second law is consistent with the first law. However, it should not be thought of as the reduction of second law to the first when no force acts on the object. Newton’s first and second laws are independent laws. They can internally be consistent with each other but cannot be derived from each other.
7. Newton’s second law is cause and effect relation. Force is the cause and acceleration is the effect. Conventionally, the effect should be written on the left and cause on the right hand side of the equation. So the correct way of writing Newton’s second law is –
m\(\overline{\mathrm{a}}\) = \(\overline{\mathrm{F}}\) or \(\frac{d \vec{p}}{d t}\) = \(\overline{\mathrm{F}}\)
![]()
Question 6.
Explain the similarities and differences of centripetal and centrifugal forces.
Answer:
Salient features of centripetal and centrifugal forces.
Centripetal Force:
- It is a real force which is exerted on the body by the external agencies like gravitational force, tension in the string, normal force etc.
- Acts in both inertial and non-inertial frames
- It acts towards the axis of rotation or center of the circle in circular motion
\(\left|\overrightarrow{\mathrm{F}}_{\mathrm{C}_{\mathrm{P}}}\right|\) = mω2r = \(\frac{m v^{2}}{r}\) - Real force and has real effects
- Origin of centripetal force is interaction between two objects.
- In inertial frames centripetal force has to be included when free body diagrams are drawn.
Centrifugal Force:
- It is a pseudo force or fictitious force which cannot arise from gravitational force, tension force, normal force etc.
- Acts only in rotating frames (non-inertial frame)
- It acts outwards from the axis of rotation or radially outwards from the center of the circular motion
\(\left|\overrightarrow{\mathrm{I}}_{\mathrm{C}_{\mathrm{f}}}\right|\) = mω2r = \(\frac{m v^{2}}{r}\) - Pseudo force but has real effects
- Origin of centrifugal force is inertia. It does not arise from interaction. In an inertial frame the object’s inertial motion appears as centrifugal force in the rotating frame.
- In inertial frames there is no centrifugal force. In rotating frames, both centripetal and centrifugal force have to be included when free body diagrams are drawn.
Question 7.
Briefly explain ‘centrifugal force’ with suitable examples.
Answer:
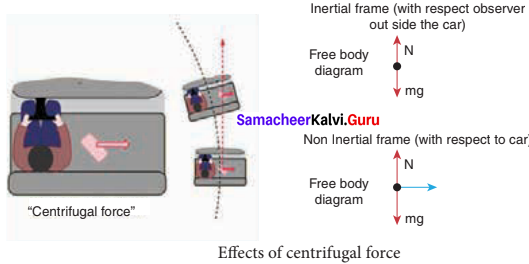
To use Newton’s first and second laws in the rotational frame of reference, we need to include a Pseudo force called centrifugal force. This centrifugal force appears to act on the object with respect to rotating frames.
Circular motion can be analysed from two different frames of reference. One is the inertial frame (which is either at rest or in uniform motion) where Newton’s laws are obeyed. The other is the rotating frame of reference which is a non – inertial frame of reference as it is accelerating.
When we examine the circular motion from these frames of reference the situations are entirely different. To use Newton’s first and second laws in the rotational frame of reference, we need to include a pseudo force called ‘centrifugal force’. This ‘centrifugal force’ appears to act on the object with respect to rotating frames. To understand the concept of centrifugal force, we can take a specific case and discuss as done below.
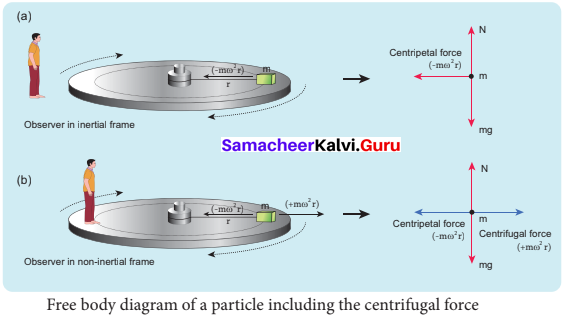
Free body diagram of a particle including the centrifugal force Consider the case of a whirling motion of a stone tied to a string. Assume that the stone has angular velocity ω in the inertial frame (at rest). If the motion of the stone is observed from a frame which is also rotating along with the stone with same angular velocity ω then, the stone appears to be at rest.
This implies that in addition to the inward centripetal force – mω2r there must be an equal and opposite force that acts on the stone outward with value +mω2r . So the total force acting on the stone in a rotating frame is equal to zero (-mω2r + mω2 r = 0). This outward force +mω2r is called the centrifugal force. The word ‘centrifugal’ means ‘flee from center’.
Note that the ‘centrifugal force’ appears to act on the particle, only when we analyse the motion from a rotating frame. With respect to an inertial frame there is only centripetal force which is given by the tension in the rstring. For this reason centrifugal force is called as a ‘pseudo force’. A pseudo force has no origin. It arises due to the non inertial nature of the frame considered. When circular motion problems are solved from a rotating frame of reference, while drawing free body diagram of a particle, the centrifugal force should necessarily be included as shown in the figure.
![]()
Question 8.
Briefly explain ‘rolling friction’.
Answer:
The invention of the wheel plays a crucial role in human civilization. One of the important applications is suitcases with rolling on coasters. Rolling wheels makes it easier than carrying luggage. When an object moves on a surface, essentially it is sliding on it. But wheels move on the surface through rolling motion. In rolling motion when a wheel moves on a surface, the point of contact with surface is always at rest. Since Rolling and kinetic friction the point of contact is at rest, there is no relative motion between the wheel and surface.
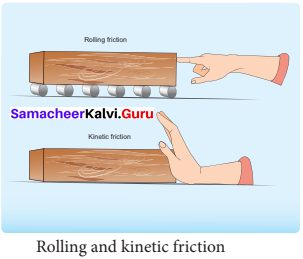
Hence the frictional fore is very less. At the same time if an object moves without a wheel, there is a relative motion between the object and the surface. As a result frictional force is larger. This makes it difficult to move the object. The figure shows the difference between rolling and kinetic friction. Ideally in pure rolling, motion of the point of contact with the surface should be at rest, but in practice it is not so.
Due to the elastic nature of the surface at the point of contact there will be some deformation on the object at this point on the wheel or surface as shown in figure. Due to this deformation, there will be minimal friction between wheel and surface. It is called ‘rolling friction. In fact, rolling friction’ is much smaller than kinetic friction.
Question 9.
Describe the method of measuring angle of repose.
Answer:
When objects are connected by strings and When objects are connected by strings and a force F is applied either vertically or horizontally or along an inclined plane, it produces a tension T in the string, which affects the acceleration to an extent. Let us discuss various cases for the same.
Case 1:
Vertical motion:
Consider two blocks of masses m1 and m2 (m1> m2) connected by a light and in extensible string that passes over a pulley as shown in Figure.
Let the tension in the string be T and acceleration a. When the system is released, both the blocks start moving, m2 vertically upward and mk, downward with same acceleration a. The gravitational force m1g on mass m1 is used in lifting the mass m2. The upward direction is chosen as y direction. The free body diagrams of both masses are shown in Figure.

Applying Newton’s second law for mass m2
T \(\hat{j}\) – m2g\(\hat{j}\) = m2a\(\hat{j}\) The left hand side of the above equation is the total force that acts on m2 and the right hand side is the product of mass and acceleration of m2 in y direction.
By comparing the components on both sides, we get
T = m2g = m2a ……….(1)
Similarly, applying Newton’s second law for mass m2
T \(\hat{j}\) – m1g\(\hat{j}\) = m1a\(\hat{j}\)
As mass mj moves downward (-\(\hat{j}\)), its acceleration is along (-\(\hat{j}\))
By comparing the components on both sides, we get
T = m1g = -m1a
m1g – T = m1a ………..(2)
Adding equations (1) and (2), we get
m1g – m2g = m1a + m2a
(m1 – m2)g = (m1 + m2)a …………(3)
From equation (3), the acceleration of both the masses is –
a = (\(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\))g ………..(4)
If both the masses are equal (m1 = m2), from equation (4)
a = 0
This shows that if the masses are equal, there is no acceleration and the system as a whole will be at rest.
To find the tension acting on the string, substitute the acceleration from the equation (4) into the equation (1).
T = m2g = m2(\(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\))
T = m2g + m2 (\(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\))g ……….(5)
By taking m2g common in the RHS of equation (5)

Equation (4) gives only magnitude of acceleration
For mass m1, the acceleration vector is given by \(\vec{a}\) = –\(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\)\(\hat{j}\)
For mass m2, the acceleration vector is given by \(\vec{a}\) = \(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\) \(\hat{j}\)
Case 2:
Horizontal motion:
In this case, mass m2 is kept on a horizontal table and mass m1, is hanging through a small pulley as shown in figure. Assume that there is no friction on the surface

As both the blocks are connected to the un stretchable string, if m1 moves with an acceleration a downward then m2 also moves with the same acceleration a horizontally.
The forces acting on mass m2 are
- Downward gravitational force (m2g)
- Upward normal force (N) exerted by the surface
- Horizontal tension (T) exerted by the string
The forces acting on mass m1 are
- Downward gravitational force (m1g)
- Tension (T) acting upwards
The free body diagrams for both the masses is shown in figure 2.

Applying Newton’s second law for m1
T\(\hat{i}\) – m1g\(\hat{j}\) = -m1a\(\hat{j}\) (alongy direction)
By comparing the components on both sides of the above equation,
T – m1g = -m1a …………(1)
Applying Newton’s second law for m2
T\(\hat{i}\) = m1a\(\hat{i}\) (along x direction)
By comparing the components on both sides of above equation,
T = m2a ………….(2)
There is no acceleration along y direction for m2.
N\(\hat{j}\) – m2g\(\hat{j}\) = 0
By comparing the components on both sides of the above equation
N – m2g = 0
N = m2g ……….(3)
By substituting equation (2) in equation (1), we can find the tension T
m2a – m1g = -m1a
m2a + m1a = m1g
a = \(\frac{m_{1}}{m_{1}+m_{2}}\)g …………(4)
Tension in the string can be obtained by substituting equation (4) in equation (2)
T = \(\frac{m_{1} m_{2}}{m_{1}+m_{2}}\)g ………..(5)
Comparing motion in both cases, it is clear that the tension in the string for horizontal motion is half of the tension for vertical motion for same set of masses and strings. This result has an important application in industries. The ropes used in conveyor belts (horizontal motion) work for longer duration than those of cranes and lifts (vertical motion).
![]()
Question 10.
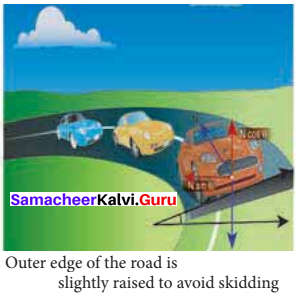
Explain the need for banking of tracks.
Answer:
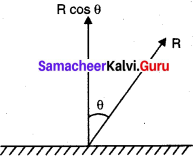
In a leveled circular road, skidding mainly depends on the coefficient of static friction py. The coefficient of static friction depends on the nature of the surface which has a maximum limiting value. To avoid this problem, usually the outer edge of the road is slightly raised compared to inner edge. This is called banking of roads or tracks. This introduces an inclination, and the angle is called banking angle. “Let the surface of the road make angle 9 with horizontal surface. Then the normal force makes the same angle 9 with the vertical. When the car takes a turn.
there are two forces acting on the car:
(a) Gravitational force mg (downwards)
(b) Normal force N (perpendicular to surface)
We can resolve the normal force into two components N cos θ and N sin θ. The component balances the downward gravitational force ‘mg’ and component will provide the necessary centripetal acceleration. By using Newton second law.
The banking angle 0 and radius of curvature of the road or track determines the safe speed of the car at the turning. If the speed of car exceeds this safe speed, then it starts to skid outward but frictional force comes into effect and provides an additional centripetal force to prevent the outward skidding.
At the same time, if the speed of the car is little lesser than safe speed, it starts to skid inward and frictional force comes into effect, which reduces centripetal force to prevent inward skidding. However if the speed of the vehicle is sufficiently greater than the correct speed, then frictional force cannot stop the car from skidding.
Question 11.
Calculate the centripetal acceleration of Moon towards the Earth.
Answer:
The centripetal acceleration is given by a = \(\frac{v^{2}}{r}\) This expression explicitly depends on Moon’s speed which is nontrivial. We can work with the formula
ω2Rm = am
am is centripetal acceleration of the Moon due to Earth’s gravity, ω is angular velocity
Rm is the distance between Earth and the Moon, which is 60 times the radius of the Earth.
Rm = 60R = 60 x 6.4 x 106 = 384 x 106 m
As we know the angular velocity ω = \(\frac { 2π}{ T }\) and T = 27.3 days = 27.3 x 24 x 60 x 60 second = 2.358 x 106 sec.
By substituting these values in the formula for acceleration
a6 = \(\frac{\left(4 \pi^{2}\right)\left(384 \times 10^{6}\right)}{\left(2.358 \times 10^{8}\right)^{2}}\) = 0.00272 ms-2
Samacheer Kalvi 11th Physics Laws of Motion Conceptual Questions
Question 1.
Why it is not possible to push a car from inside?
Answer:
While trying to push a car from outside, he pushes the ground backwards at an angle. The ground offers an equal reaction in the opposite direction, so car can be moved. But the person sits inside means car and the person becomes a single system, and the force given will be a internal force. According to Newton’s third law, total internal force acting on the system is zero and it cannot accelerate the system.
Question 2.
There is a limit beyond which the polishing of a surface increases frictional resistance rather than decreasing it why?
Answer:
Friction is a contact force. Friction is directly proportional to area of contact. In the normal surfaces there are bumps to interlock the surfaces in contact. But the surfaces are polished beyond certain limit. The area of contact will be increased and the molecules come closer to each other. It increases electrostatic force between the molecules. As a result it increases friction.
![]()
Question 3.
Can a single isolated force exist in nature? Explain your answer.
Answer:
No. According to Newton’s third law, for every action, there is an equal and opposite reaction. So, whatever case we consider, if there is an action there is always a reaction. So it is impossible.
Question 4.
Why does a parachute descend slowly?
Answer:
A parachute descends slowly because the surface area of parachute is large so that air gives more resistance when it descends down.
Question 5.
When walking on ice one should take short steps. Why?
Answer:
Let R represent the reaction offered by the ground. The vertical component R cos θ will balance the weight of the person and the horizontal component R sin θ will help the person to walk forward.
Now, normal reaction = R cos θ
Friction force = R sin θ
Coefficient of friction, µ = \(\frac {R sin θ}{R cos θ }\) = tan θ
In a long step, θ is more. So tan θ is more. But p has a fixed value. So, there is danger of slipping in a long step.
Question 6.
When a person walks on a surface, the frictional force exerted by the surface on the person is opposite to the direction of motion. True or false?
Answer:
False. In frictional force exerted by the surface on the person is in the direction of his motion. Frictional force acts as an external force to move the person. When the person trying to move, he gives a push to ground on the backward direction and by Newton’s third law he is pushed by the ground in the forward direction. Hence frictional force acts along the direction of motion.
![]()
Question 7.
Can the coefficient of friction be more than one?
Answer:
Yes. The coefficient of friction can be more than one in some cases such as silicone rubber. Coefficient of friction is the ratio of frictional force to normal force, i.e. F = μR. If p is greater than one means frictional force is greater than normal force. But in general case the value is usually between 0 and 1.
Question 8.
Can we predict the direction of motion of a body from the direction of force on it?
Answer:
Yes. The direction of motion is always opposite to the force of kinetic friction. By using the principle of equilibrium, the direction of force of static friction can be determined. When the object is in equilibrium, the frictional force must point in the direction which results as a net force is zero.
Question 9.
The momentum of a system of particles is always conserved. True or false?
Answer:
True. The total momentum of a system of particles is always constant i.e. conserved. When no external force acts on it.
Samacheer Kalvi 11th Physics Laws of Motion Numerical Problems
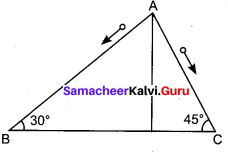
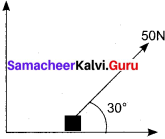
Question 1.
A force of 50 N act on the object of mass 20 kg. shown in the figure. Calculate the acceleration of the object in x and y directions.
Answer:
Given F = 50 N and m = 20 kg
(1) component of force along x – direction
Fx = F cos θ
= 50 x cos 30° = 43.30 N
ax = \(\frac{F_{x}}{m}\) = \(\frac {43.30}{20}\) =2.165 ms-2
(2) Component of force along y – direction
Fy = F sin θ = 50 sin 30° = 25 N
ay = \(\frac{F_{y}}{m}\) = \(\frac {25}{20}\) = 1.25 ms-2
Question 2.
A spider of mass 50 g is hanging on a string of a cob web as shown in the figure. What is the tension in the string?
Answer:
Given m = 50 g, T = ?
Tension in the string T = mg
= 50 x 10-2 x 9.8 = 0.49 N
Question 3.
What is the reading shown in spring balance?
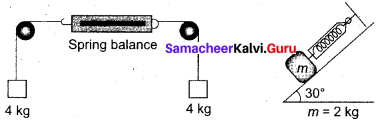
Answer:
When a spring balance hung on a rigid support and load is attached at its other end, the weight of the load exerts a force on the rigid support in turn support exerts equal and opposite force on that load, so that balance will be stretched. This is the principle of spring balance. Flence the answer is 4 kg.
Given: m = 2 kg, 0 = 30°.
Resolve the weight into its component as mg sin θ and mg cos θ.
Here mg sin θ acts parallel to the surface
∴ W = mg sin θ
= 2 x 9.8 x sin 30° = 2 x 9.8 x \(\frac {1}{2}\) = 9.8 N
![]()
Question 4.
The physics books are stacked on each other in the sequence: +1 volumes 1 and 2; +2 volumes 1 and 2 on a table
(a) Identify the forces acting on each book and draw the free body diagram.
(b) Identify the forces exerted by each book on the other.
Answer:
Let m1, m2, m3, m4, are the masses of +1 volume I and II and +2 volumes I & II
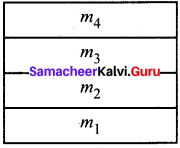
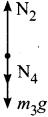
(a) Force on book m4
- Downward gravitational force acting downward (m3g)
- Upward normal force (N3) exerted by book of mass m3
 |
|
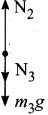
(b) Force on book m3
- Downward gravitational force (m3g)
- Downward force exerted by m4 (N4)
- Upward force exerted by m2 (N2)
(c) Force on book m2
- Downward gravitational force (m2g)
- Downward force exerted by m3 (N3)
- Upward force exerted by m1 (CN1)
(d) Force on book m1
- Downward gravitational force exerted by earth (m1g)
- Downward force exerted by m2 (N2)
- Upward force exerted by the table (Ntable)
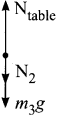
Question 5.
A bob attached to the string oscillates back and forth. Resolve the forces acting on the bob in to components. What is the acceleration experienced by the bob at an angle θ.
Answer:
The gravitational force (mg) acting downward can be resolved into two components as mg cos θ and mg sin θ
T – tension exerted by the string.
Tangential force FT = maT = mg sin θ
∴ Tangential acceleration aT = g sin θ
Centripetal force Fc = mac = T – mg cos θ
ac = \(\frac { T – mg cos θ }{ m }\)
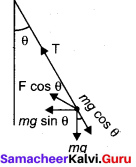
Question 6.
Two masses m1 and m2 are connected with a string passing over a friction-less pulley fixed at the comer of the table as shown in the figure. The coefficient of static friction of mass m1 with the table is µs Calculate the minimum mass m3 that may be placed on m1to prevent it from sliding. Check if m1 = 15 kg, m2 = 10 kg, m3 = 25 and µs = 0.2.
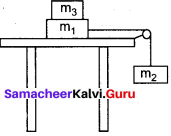
Solution:
Let m3 is the mass added on m1
Maximal static friction
\(f_{s}^{\max }\) = µsN = µs (m1 + m3 )g
Here
N = (m1 + m3 )g
Tension acting on string = T = m2 g
Equate (1) and (2)
µs(m1 + m3) = m2g
µsm1 + µsm3 = m2
m3 = \(f_{s}^{\max }\) – m1
(ii) Given,
m1 = 15 kg, m2 = 10 kg : m3 = 25 kg and µs = 0.2
m3 = \(f_{s}^{\max }\) – m1
m3 = \(\frac {10}{ 0.2 }\) – 15 = 50 – 15 = 35 kg
The minimum mass m3 = 35 kg has to be placed on ml to prevent it from sliding. But here m3 = 25 kg only.
The combined masses (m1 + m3) will slide.
Question 7.
Calculate the acceleration of the bicycle of mass 25 kg as shown in Figures 1 and 2.
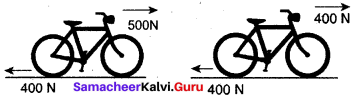
Answer:
Given:
Mass of bicycle m = 25 kg
Fig. I:
Net force acting in the forward direction, F = 500 – 400 = 100 N
acceleration a = \(\frac { F}{ m }\) = \(\frac { 100 }{25}\) = 4 ms-2
Fig. II:
Net force acting on bicycle F = 400 – 400 = 0
∴ acceleration a = \(\frac { F}{ m }\) = \(\frac { 0}{25}\) = 0
![]()
Question 8.
Apply Lami’s theorem on sling shot and calculate the tension in each string?
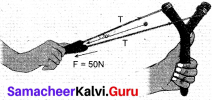
Answer:
Given F = 50 N, θ = 30°
Here T is resolved into its components as T sin θ and T cos θ as shown.
According to Lami’s theorem,
\(\frac { F}{sin θ}\) = \(\frac { T}{sin (180 – θ)}\) = \(\frac { T}{sin (180 – θ)}\)
\(\frac { F}{sin θ}\) = \(\frac { T}{sin θ}\)
\(\frac { F}{2 sin θ cos θ}\) = \(\frac { T}{sin θ}\) [T = \(\frac { T}{2 cos θ}\) ]
T = \(\frac {T}{2 cos θ}\) = \(\frac { 50}{ 2 cos 30}\) = 28.868 N
Question 9.
A football player kicks a 0.8 kg ball and imparts it a velocity 12 ms-1. The contact between the foot and ball is only for one – sixtieth of a second. Find the average kicking force.
Answer:
Given,
Mass of the ball = 0.8 kg
Final velocity (V) =12 ms-1 and time t =\(\frac {1}{60}\) s
Initial velocity = 0
We know the average kicking force
F = ma = \(\frac {m(v – u)}{t}\) = \(\frac{0.8(12-0)}{\left(\frac{1}{60}\right)}\)
F = 576 N
Question 10.
A stone of mass 2 kg is attached to a string of length 1 meter. The string can withstand maximum tension 200 N. What is the maximum speed that stone can have during the whirling motion?
Solution:
Given,
Mass of a stone = 2 kg,
length of a string = 1 m
Maximum tension = 200 N
The force acting on a stone in the whirling motion is centripetal force. Which is provided by tension of the string.
Tmax = Fmax = \(\frac{m \mathrm{V}_{\mathrm{max}}^{2}}{r}\)
200 = \(v_{\max }^{2}\) = 100
\(v_{\max }^{2}\) = 10 ms-1
![]()
Question 11.
Imagine that the gravitational force between Earth and Moon is provided by an invisible string that exists between the Moon and Earth. What is the tension that exists in this invisible string due’ to Earth’s centripetal force? (Mass of the Moon = 7.34 x 1022 kg, Distance between Moon and Earth = 3.84 x 108 m).
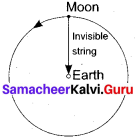
Solution:
Given,
Mass of the moon = 7.34 x 1022 kg
Distance between moon and earth = 3.84 x 108 m
Centripetal force = F = \(\frac{m \mathrm{V}^{2}}{r}\) = \(\frac{7.34 \times 10^{22} \times\left(1.023 \times 10^{3}\right)^{2}}{3.84 \times 10^{8}}\) = 2 x 1020
Question 12.
Two bodies of masses 15 kg and 10 kg are connected with light string kept on a smooth surface. A horizontal force F = 500 N is applied to a 15 kg as shown in the figure. Calculate the tension acting in the string.
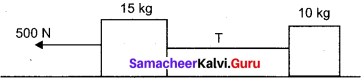
Answer:
Given,
m1 = 15 kg, m2 = 10 kg, F = 500 N
Tension acting in the string T = \(\frac{m_{2}}{m_{1}+m_{2}}\) F
T = \(\frac {10}{25}\) x 500 = 200 N
Question 13.
People often say “For every action there is an equivalent opposite reaction”. Here they meant ‘action of a human’. Is it correct to apply Newton’s third law to human actions? What is meant by ‘action’ in Newton third law? Give your arguments based on Newton’s laws.
Answer:
Newton’s third law is applicable to only human’s physical actions which involves physical force. Third law is not applicable to human’s psychological actions or thoughts.
Question 14.
A car takes a turn with velocity 50 ms-1 on the circular road of radius of curvature To m. Calculate the centrifugal force experienced by a person of mass 60 kg inside the car?
Answer:
Given,
Mass of a person = 60 kg
Velocity of the car = 50 ms-1
Radius of curvature = 10 m
Centrifugal force F = \(\frac{m \mathrm{V}^{2}}{r}\) = \(\frac{60 \times(50)^{2}}{10}\) = 15,000 N
Question 15.
A long stick rests on the surface. A person standing 10 m away from the stick. With what minimum speed an object of mass 0.5 kg should he thrown so that it hits the stick. (Assume the coefficient of kinetic friction is 0.7).
Answer:
Given,
Distance (s) = 10 m
Mass of the object (m) = 0.5 kg
Coefficient of kinetic friction (µ) = 0.7
Work done in moving a body in horizontal surface ω = µR x s = µmg x s
This work done is equal to initial kinetic energy of the object
\(\frac{1}{2} m v^{2}\) = µ mg s
\(\left|v^{2}\right|\) = 2 µgs = 2 x 0.7 x 9.8 x 10
v2 = 14 x 9.8 = 137. 2
v = 11. 71 ms-1
Samacheer Kalvi 11th Physics Laws of Motion Additional Questions Solved
Samacheer Kalvi 11th Physics Laws of Motion Multiple Choice Questions
Question 1.
The concept “force causes motion” was given by –
(a) Galileo
(b) Aristotle
(c) Newton
(d) Joule
Answer:
(b) Aristotle
Question 2.
Who decoupled the motion and force?
(a) Galileo
(b) Aristotle
(c) Newton
(d) Joule
Answer:
(a) Galileo
Question 3.
The inability of objects to move on its own or change its state of motion is called as –
(a) force
(b) momentum
(c) inertia
(d) impulse
Answer:
(c) inertia
Question 4.
Inertia means –
(a) inability
(b) resistance to change its state
(c) movement
(d) inertial frame
Answer:
(b) resistance to change its state
Question 5.
When a bus starts to move from rest, the passengers experience a sudden backward push is an example for –
(a) Inertia of motion
(b) Inertia of direction
(c) Inertia of rest
(d) back pull
Answer:
(c) Inertia of rest
![]()
Question 6.
If the brake is applied in the moving bus suddenly, passengers move forward is an example for –
(a) Inertia of motion
(b) Inertia of direction
(c) Inertia of rest
(d) back pull
Answer:
(a) Inertia of motion
Question 7.
In whirling motion, if the string is cut suddenly, the stone moves tangential to circle is an –
(a) Inertia of motion
(b) Inertia of direction
(c) Inertia of rest
(d) back pull
Answer:
(b) Inertia of direction
Question 8.
Newtons laws are applicable in –
(a) Inertial frame
(b) non inertial frame
(c) in any frame
(d) none
Answer:
(a) Inertial frame
Question 9.
The accelerated train is an example for –
(a) inertial frame
(b) non-inertial frame
(c) both (a) and (b)
(d) none of the above
Answer:
(b) non-inertial frame
![]()
Question 10.
Rate of change of momentum of an object is equal to –
(a) acceleration
(b) work done
(c) force
(d) impulse
Answer:
(c) force
Question 11.
The product of mass and velocity is –
(a) force
(b) impulse
(c) momentum
(d) acceleration
Answer:
(c) momentum
Question 12.
Unit of momentum –
(a) kg ms-2
(b) kg ms-1
(c) MLT-2
(d) MLT-1
Answer:
(b) kg ms-1
Question 13.
According to Newton’s third law –
(a) F12 = F21
(*) F12 = -F21
(c) F12 + F21 = 0
(d) F12 x F21 = 0
Answer:
(a) F12 = F21
Question 14.
According to Newton’s third law –
(a) \(\overrightarrow{\mathrm{F}_{12}}=\overrightarrow{\mathrm{F}_{21}}\)
(b) \(\overrightarrow{\mathrm{F}_{12}}=-\overrightarrow{\mathrm{F}_{21}}\)
(c) \(\mathrm{F}_{12}+\mathrm{F}_{21}\) = 0
(d) \(\mathrm{F}_{12}x\mathrm{F}_{21}\) = 0
Answer:
(b) \(\overrightarrow{\mathrm{F}_{12}}=-\overrightarrow{\mathrm{F}_{21}}\)
Question 15.
The law which is valid in both inertial and non-inertial frame is –
(a) Newton’s first law
(b) Newton’s second law
(c) Newton’s third law
(d) none
Answer:
(c) Newton’s third law
![]()
Question 16.
When a force is applied on a body, it can change –
(a) velocity
(b) momentum
(c) direction of motion
(d) all the above
Answer:
(d) all the above
Question 17.
The rate of change of velocity is 1 ms-2 when a force is applied on the body of mass 75 gm the force is –
(a) 75 N
(b) 0.75 N
(c) 0.075 N
(d) 0.75 x 10-3 N
Answer:
(c) Force is given by
F = m a
= 75 gm x 1 cm s-2 = 75 x 10-3 x 1 = 75 x 10-3 = 0.075 N
Question 18.
The action and reaction forces acting on –
(a) same body
(b) different bodies
(c) either same or different bodies
(d) none of the above
Answer:
(b) different bodies
Question 19.
Newton’s first law of motion gives the concept of –
(a) velocity
(b) energy
(c) momentum
(d) Inertia
Answer:
(d) Inertia
Question 20.
Inertia of a body has direct dependence on –
(a) velocity
(b) area
(c) mass
(d) volume
Answer:
(c) mass
![]()
Question 21.
If a car and a scooter have the same momentum, then which one is having greater speed?
(a) scooter
(b) car
(c) both have same velocity
(d) data insufficient
Answer:
(a) scooter
Question 22.
Newton’s second law gives –
(a) \(\overrightarrow{\mathrm{F}} \propto \frac{d \overrightarrow{\mathrm{P}}}{\mathrm{dt}}\)
(b) \(\overrightarrow{\mathrm{F}}=\frac{d \overrightarrow{\mathrm{P}}}{\mathrm{dt}}\)
(c) \(\overrightarrow{\mathrm{F}}=m \vec{a}\)
(d) all the above
Answer:
(d) all the above
Question 23.
1 dyne is –
(a) 105N
(b) 10-5N
(c) 1N
(d) 10-3N
Answer:
(b) 10-5N
Question 24.
If same force is acting on two masses m1 and m2, and the accelerations of two bodies are a1 and a2 respectively, then –
(a) \(\frac{a_{2}}{a_{1}}=\frac{m_{2}}{m_{1}}\)
(b) \(\frac{a_{1}}{a_{2}}=\frac{m_{1}}{m_{2}}\)
(c) \(\frac{a_{1}}{a_{2}}=\frac{m_{2}}{m_{1}}\)
(d) m1 a1 + m2a2 = 0
Answer:
(c) \(\frac{a_{1}}{a_{2}}=\frac{m_{2}}{m_{1}}\)
Question 25.
If a force \(\overline{\mathrm{F}}\) = 3\(\hat{i}\) – 4\(\hat{j}\) N produces an acceleration of 10 ms-2 on a body, then the mass of a body is –
(a) 10 kg
(b) 9 kg
(c) 0.9 kg
(d) 0.5 kg
Answer:
\(\overline{\mathrm{F}}\) = 3\(\hat{i}\) – 4\(\hat{j}\)
Magnitude:
|\(\overline{\mathrm{F}}\)| = \(\sqrt{9+16}\) = \(\sqrt{25}\) = 5N
F = ma
⇒ m = \(\frac{|\mathrm{F}|}{a}\) = \(\frac{5}{10}\) = \(\frac{1}{2}\) = 0.5 kg
Question 26.
A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 ms-1. How long does the body take to stop?
(a) 0.75 s
(b) 1.33 s
(c) 6 s
(d) 35 s
Answer:
Acceleration a = \(\frac{-F}{m}\) = \(\frac{50}{20}\) = – 2.5 ms-2
u = l5 ms-1
v = 0
t = ?
v = u + at
0 = 15 – 2.5t
t = \(\frac{15}{2.5}\) = 6s
Question 27.
Rain drops come down with –
(a) zero acceleration and non zero velocity
(b) zero velocity with non zero acceleration
(c) zero acceleration and non zero net force
(d) none
Answer:
(a) zero acceleration and non zero velocity
![]()
Question 28.
If force is the cause then the effect is –
(a) mass
(b) potential energy
(c) acceleration
(d) Inertia
Answer:
(c) acceleration
Question 29.
In free body diagram, the object is represented by a –
(a) line
(b) arrow
(c) circle
(d) point
Answer:
(d) point
Question 30.
When an object of mass m slides on a friction less surface inclined at an angle 0, then normal force exerted by the surface is –
(a) g cos θ
(b) mg cos θ
(c) g sin θ
(d) mg tan θ
Answer:
(b) mg cos θ
Question 31.
The acceleration of the sliding object in an inclined plane –
(a) g cos θ
(b) mg cos θ
(c) g sin θ
(d) mg sin θ
Answer:
(c) g sin θ
Question 32.
The speed of an object sliding in an inclined plane at the bottom is –
(a) mg cos θ
(b) \(\sqrt{2 s g sin θ}\)
(c) \(\sqrt{2 s g cos θ}\)
(d) \(\sqrt{2 s g tan θ}\)
Answer:
(b) \(\sqrt{2 s g sin θ}\)
![]()
Question 33.
The acceleration of two bodies of mass m1 and m2 in contact on a horizontal surface is –
(a) \(a=\frac{\mathbf{F}}{m_{1}}\)
(b) \(a=\frac{F}{m_{2}}\)
(c) \(a=\frac{\mathrm{F}}{m_{1}+m_{2}}\)
(d) \(a=\frac{\mathrm{F}}{m_{1} m_{2}}\)
Answer:
(c) \(a=\frac{\mathrm{F}}{m_{1}+m_{2}}\)
Question 34.
Two blocks of masses m1 and m2 (m1 > m2) in contact with each other on frictionless, horizontal surface. If a horizontal force F is given on m1, set into motion with acceleration a, then reaction force on mass m1 by m2, is –
(a) \(\frac{\mathrm{F} m_{1}}{m_{1}+m_{2}}\)
(b) \(\frac{m_{1} m_{2}}{\mathrm{F} m_{1}}\)
(c) \(\frac{m_{1} m_{2}}{\mathrm{F} m_{2}}\)
(d) \(\frac{\mathrm{F} m_{2}}{m_{1}+m_{2}}\)
Answer:
(d) \(\frac{\mathrm{F} m_{2}}{m_{1}+m_{2}}\)
Question 35.
If two masses m1 and m2 (m1 > m2) tied to string moving over a frictionless pulley, then acceleration of masses –
(a) \(\frac{\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\) g
(b) \(\frac{m_{1}+m_{2}}{\left(m_{1}-m_{2}\right)}\) g
(c) \(\frac{2 m_{1} m_{2}}{m_{1}+m_{2}}\) g
(d) \(\frac{m_{1} m_{2}}{2 m_{1} m_{2}}\) g
Answer:
(a) \(\frac{\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\) g
Question 36.
if two masses m1 and m2 (m1 > m2)tied to string moving over a frictionless pulley, then acceleration of masses –
(a) \(\frac{\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\) g
(b) \(\frac{m_{1}+m_{2}}{\left(m_{1}-m_{2}\right)}\) g
(c) \(\frac{2 m_{1} m_{2}}{m_{1}+m_{2}}\) g
(d) \(\frac{m_{1} m_{2}}{2 m_{1} m_{2}}\) g
Answer:
(a) \(\frac{\left(m_{1}-m_{2}\right)}{m_{1}+m_{2}}\) g
Question 37.
Three massses is in contact as shown. If force F is applied to mass m1, the acceleration of three masses is –
(a) \(\frac{\mathrm{F}}{m_{1}+m_{2}+m_{3}}\)
(b) \(\frac{m_{1} F}{\left(m_{1}+m_{2}+m_{3}\right)}\)
(c) \(\frac{\left(m_{2}+m_{3}\right) F}{\left(m_{1}+m_{2}+m_{3}\right)}\)
(d) \(\frac{m_{3} \mathrm{F}}{m_{1}+m_{2}+m_{3}}\)
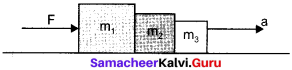
Answer:
(a) \(\frac{\mathrm{F}}{m_{1}+m_{2}+m_{3}}\)
![]()
Question 38.
Three masses in contact is as shown above. If force F is applied to mass m1 then the contact force acting on mass m2 is –
(a) \(\frac{\mathrm{F}}{m_{1}+m_{2}+m_{3}}\)
(b) \(\frac{m_{1} F}{\left(m_{1}+m_{2}+m_{3}\right)}\)
(c) \(\frac{\left(m_{2}+m_{3}\right) F}{\left(m_{1}+m_{2}+m_{3}\right)}\)
(d) \(\frac{m_{3} \mathrm{F}}{m_{1}+m_{2}+m_{3}}\)
Answer:
(c) \(\frac{\left(m_{2}+m_{3}\right) F}{\left(m_{1}+m_{2}+m_{3}\right)}\)
Question 39.
Three masses is contact as shown. It force F is applied to mass m1, then the contact force acting on mass m3 is –
(a) \(\frac{\mathrm{F}}{m_{1}+m_{2}+m_{3}}\)
(b) \(\frac{m_{1} F}{\left(m_{1}+m_{2}+m_{3}\right)}\)
(c) \(\frac{\left(m_{2}+m_{3}\right) F}{\left(m_{1}+m_{2}+m_{3}\right)}\)
(d) \(\frac{m_{3} \mathrm{F}}{m_{1}+m_{2}+m_{3}}\)
Answer:
(d) \(\frac{m_{3} \mathrm{F}}{m_{1}+m_{2}+m_{3}}\)
Question 40.
Two masses connected with a string. When a force F is applied on mass m2. The acceleration produced is –
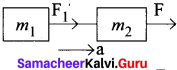
(a) \(\frac{\mathrm{F}}{m_{1}+m_{2}}\)
(b) \(\frac{\mathbf{F}}{m_{1}-m_{2}}\)
(c) \(\frac{m_{1}+m_{2}}{\mathrm{F}}\)
(d) \(\frac{m_{3} \mathrm{F}}{m_{1}+m_{2}+m_{3}}\)
Answer:
(a) \(\frac{\mathrm{F}}{m_{1}+m_{2}}\)
Question 41.
Two masses connected with a string. When a force F is applied on mass m2. The force acting on m1 is –
(a) \(\frac{m_{1} \mathrm{F}}{m_{1}+m_{2}}\)
(b) \(\frac{m_{2} \mathrm{F}}{m_{1}+m_{2}}\)
(c) \(\frac{m_{1}+m_{2}}{m_{1}} \mathbf{F}\)
(d) \(\frac{m_{1}+m_{2}}{m_{2}} \mathbf{F}\)
Answer:
(b) \(\frac{m_{2} \mathrm{F}}{m_{1}+m_{2}}\)
Question 42.
If a block of mass m lying on a frictionless inclined plane of length L height h and angle of inclination θ, then the velocity at its bottom is –
(a) g sin θ
(b) g cos θ
(c) \(\sqrt{2 g h}\)
(d) \(\sqrt{2 a sin θ}\)
Answer:
(c) \(\sqrt{2 g h}\)
![]()
Question 43.
If a block of mass m lying on a frictionless inclined plane of length L, height h and angle of inclination θ, then the time take taken to reach the bottom is –
(a) g sing θ
(b) sin θ \(\sqrt{\frac{2 h}{g}}\)
(c) sin θ \(\sqrt{\frac{g}{h}}\)
(d) \(\frac{1}{\sin \theta} \sqrt{\frac{2 h}{g}}\)
Answer:
(d) \(\frac{1}{\sin \theta} \sqrt{\frac{2 h}{g}}\)
Question 44.
A rocket works on the principle of conservation of –
(a) energy
(b) mass
(c) angular momentum
(d) linear momentum
Answer:
(b) mass
Question 45.
A bomb at rest explodes. The total momentum of all its fragments is –
(a) zero
(b) infinity
(c) always 1
(d) always greater then 1
Answer:
(a) zero
Question 46.
A block of mass m1 is pulled along a horizontal friction-less surface by a rope of mass m2 If a force F is given at its free end. The net force acting on the block is –
(a) \(\frac{m_{1} \mathrm{F}}{m_{1}-m_{2}}\)
(b) F
(c) \(\frac{m_{2} \mathrm{F}}{\left(m_{1}+m_{2}\right)}\)
(d) \(\frac{m_{1} \mathrm{F}}{\left(m_{1}+m_{2}\right)}\)
Answer:
(b) F
Question 47.
A block of mass m is pulled along a horizontal surface by a rope. The tension in the rope will be same at all the points –
(a) if the rope is accelerated
(b) if the rope is mass less
(c) always
(d) none of the above
Answer:
(b) if the rope is mass less
![]()
Question 48.
The lines of forces act at a common point is called as –
(a) concurrent forces
(b) co-planar forces
(c) equilibrium
(d) resultant
Answer:
(a) concurrent forces
Question 49.
If the lines of forces act in the same plane, they can be –
(a) concurrent forces
(b) coplanar forces
(c) either concurrent force or coplanar forces
(d) Lami’s force
Answer:
(d) concurrent forces
Question 50.
Lami’s theorem is applicable only when the system of forces are is –
(a) same plane
(b) different plane
(c) equilibrium
(d) none of the above
Answer:
(c) equilibrium
Question 51.
Due to the action of internal forces of the system, the total linear momentum of the system is –
(a) a variable
(b) a constant
(c) always zero
(d) always infinity
Answer:
(c) always zero
Question 52.
The velocity with which a gun suddenly moves backward after firing is –
(a) linear velocity
(b) positive velocity
(c) recoil velocity
(d) v1 + v2
Answer:
(c) recoil velocity
![]()
Question 53.
If a very large force acts on an object for a very short duration, then the force is called as –
(a) Newtonian force
(b) impulsive force
(c) concurrent force
(d) coplanar force
Answer:
(A) impulsive force
Question 54.
The unit of impulse is –
(a) Nm
(b) Ns
(c) Nm2
(d) Ns-2
Answer:
(b) Ns
Question 55.
The force which always opposes the relative motion between an object and the surface where it is placed is –
(a) concurrent force
(b) frictional force
(c) impulsive force
(d) coplanar force
Answer:
(b) frictional force
Question 56.
The force which opposes the initiation of motion of an object on the surface is –
(a) static friction
(b) kinetic friction
(c) friction
(d) zero
Answer:
(d) static friction
Question 57.
When the object is at rest, the resultant of gravitational force and upward normal force is –
(a) Static force
(b) zero
(c) one
(d) infinity
Answer:
(b) zero
Question 58.
The magnitude of static frictional force d lies between –
(a) 0 ≤ f ≤ µsN
(b) 0 ≥f ≥ µsN
(c) 0 and 1
(d) 0 and minimal static frictional force.
Answer:
(a) 0 ≤ f ≤ µsN
Question 59.
The unit of co-efficient of static friction is –
(a) N
(b) N m
(c) N s
(d) no unit
Answer:
(d) no unit
![]()
Question 60.
If the object is at rest and no external force is applied on the object, the static friction acting on the object is –
(a) µsN
(b) zero
(c) one
(d) infinity
Answer:
(d) no unit
Question 61.
When object begins to slide, the static friction acting on the object attains –
(a) zero
(b) minimum
(c) maximum
(d) infinity
Answer:
(c) maximum
Question 62.
The static friction does not depend upon –
(a) the area of contact
(b) normal force
(c) the magnitude of applied force
(d) none of the above
Answer:
(a) the area of contact
Question 63.
Which of the following pairs of materials has minimum amount of coefficient of static friction is –
(a) Glass and glass
(b) wood and wood
(c) ice and ice
(d) steel and steel
Answer:
(c) ice and ice
Question 64.
Kinetic friction is also called as –
(a) sliding friction
(b) dynamic friction
(c) both (a) and (b)
(d) static friction
Answer:
(c) both (a) and (b)
![]()
Question 65.
The unit of coefficient of kinetic friction is/has –
(a) Nm
(b) Ns
(c) Nm2
(d) no unit
Answer:
(d) no unit
Question 66.
The nature of materials in mutual contact decides –
(a) µs
(b) µk
(c) µs or µk
(d) none
Answer:
(c) µs or µk
Question 67.
Coefficient of kinetic friction is less than –
(a) O
(b) one
(c) µs
(d) µsN
Answer:
(c) µs
Question 68.
The static friction –
(a) increases linearly
(b) is constant
(c) zero
(d) varies parabolically
Answer:
(a) increases linearly
Question 69.
The kinetic friction –
(a) increases linearly
(b) is constant
(c) zero
(d) varies parabolically
Answer:
(b) is constant
![]()
Question 70.
Kinetic friction is independent of –
(a) nature of materials
(b) temperature of the surface
(c) applied force
(d) none of the above
Answer:
(c) applied force
Question 71.
The angle between the normal force and the resultant force of normal force and maximum frictional force is –
(a) angle of friction
(b) angle of repose
(c) angle of inclination
(d) none of the above
Answer:
(a) angle of friction
Question 72.
The angle friction θ is given by –
(a) tan µs
(b) tan-1 µs
(c) \(\frac{f S^{\mathrm{max}}}{N}\)
(d) sin-1 µs
Answer:
(b) tan-1 µs
Question 73.
The angle of inclined plane with the horizontal such that an object placed on it begins to slide is –
(a) angle of friction
(b) angle of repose
(c) angle of response
(d) angle of retardation
Answer:
(b) angle of repose
Question 74.
Comparatively, which of the following has lesser value than others?
(a) static friction
(b) kinetic friction
(c) Rolling friction
(d) skiping friction
Answer:
(c) Rolling friction
![]()
Question 75.
The origin of friction is –
(a) electrostatic interaction
(b) electromagnetic interaction magnetic
(c) photon interaction
(d) interaction
Answer:
(b) electromagnetic interaction
Question 76.
Friction can be reduced by –
(a) polishing
(b) lubricating
(c) using ball bearings
(d) all the above
Answer:
(c) using ball bearings
Question 77.
For a particle revolving in a circular path, the acceleration of the particle is –
(a) along the tangent
(b) along the radius
(c) along the circumference of the circle
(d) zero
Answer:
(b) along the radius
Question 78.
A particle moves along a circular path under the action of a force. The work done by the force is –
(a) Positive and non zero
(b) zero
(c) Negative and non zero
(d) none of the above
Answer:
(b) zero
Question 79.
A bullet hits and gets embedded in a solid block resting on a horizontal frictionless table. Which of the following is conserved?
(a) Momentum and kinetic energy
(b) kinetic energy alone
(c) Momentum alone
(d) potential energy alone
Answer:
(c) Momentum alone
Question 80.
The origin of the centripetal force can be –
(a) gravitational force
(b) frictional force
(c) coulomb force
(d) all the above
Answer:
(d) all the above
Question 81.
Centripetal acceleration is –
(a) \(\frac{m v^{2}}{r}\)
(b) \(\frac{v^{2}}{r}\)
(c) r v2
(d) rω
Answer:
(b) \(\frac{v^{2}}{r}\)
![]()
Question 82.
Centripetal acceleration is –
(a) \(\frac{m v^{2}}{r}\)
(b) r ω2
(c) rv2
(d) rω
Answer:
(c) rω2
Question 83.
The centripetal force is –
(a) \(\frac{m v^{2}}{r}\)
(b) rω2
(c) both (a) and (b)
(d) none
Answer:
(c) both (a) and (b)
Question 84.
When a car is moving on a circular track the centripetal force is due to –
(a) gravitational force
(b) frictional force
(c) magnetic force
(d) elastic force
Answer:
(b) frictional force
Question 85.
If the road is horizontal then the normal force and gravitational force are –
(a) equal and along the same direction
(b) equal and opposite
(c) unequal and along the same direction
(d) unequal and opposite
Answer:
(b) equal and opposite
Question 86.
The velocity of a car for safe turn on leveled circular road –
(a) \(v \leq \sqrt{\mu_{s} r g}\)
(b) \(v \geq \sqrt{\mu_{s} r g}\)
(c) \(v=\sqrt{\mu_{s} rg}\)
(d) \(v \leq \mu_{s} rg\)
Answer:
(a) \(v \leq \sqrt{\mu_{s} r g}\)
Question 87.
In a leveled circular road, skidding mainly depends on –
(a) µs
(b) µk
(c) acceleration
(d) none
Answer:
(a) µs
Question 88.
The speed of a car to move on the banked road so that it will have safe turn is –
(a) µsrg
(b) \(\sqrt{r g \tan \theta}\)
(c) rg tan θ
(d) r2g tan θ
Answer:
(b) \(\sqrt{r g \tan \theta}\)
Question 89.
Centrifugal force is a –
(a) pseudo force
(b) real force
(c) forced acting towards center
(d) none of the above
Answer:
(a) pseudo force
Question 90.
Origin of centrifugal force is due to –
(a) interaction between two
(b) inertia
(c) electromagnetic interaction
(d) inertial frame
Answer:
(b) inertia
Question 91.
Centripetal force acts in –
(a) inertial frame
(b) non inertial frame
(c) both (a) and (h)
(d) linear motion
Answer:
(c) both (a) and (b)
![]()
Question 92.
Centrifugal force acts in –
(a) inertial frame
(b) non inertial frame
(c) both (a) and (b)
(d) linear motion
Answer:
(b) non inertial frame
Question 93.
A cricket ball of mass loo g moving with a velocity of 20 ms-1 is brought to rest by a player in 0.05s the impulse of the ball is –
(a) 5 Ns
(b) – 2 Ns
(c) – 2.5 Ns
(d) zero
Answer:
(b) – 2 Ns
mass = 0.1 kg
Initial velocity t = 20 ms-1
Final velocity y = 0
Change in momentum in impulse = m(v – u) = 0.1(0 – 20) = – 2 Ns
Question 94.
If a stone tied at the one end of a string of length 0.5 m is whirled in a horizontal circle with a constant speed 6 ms-1 then the acceleration of the shone is –
(a) 12 ms-2
(b) 36 ms-2
(c) 2π2 ms-2
(d) 72 ms-2
Answer:
(d) Centripetal acceleration = \(\frac{v^{2}}{r}\) = \(\frac{6^{2}}{0.5}\) = \(\frac{36}{0.5}\) = 72 ms-2
![]()
Question 95.
A block of mass 3 kg is at rest on a rough inclined plane with angle of inclination 30° with horizontal. If .is 0.7, then the frictional force is –
(a) 17.82 N
(b) 1.81 N
(c) 3.63 N
(d) 2.1 N
Answer:
(a) Frictional force = µmg cos θ = 0.7 x 3 x 9.8 cos 30° = 17.82 N
Question 96.
Two masses 2 kg and 4 kg are tied at the ends of a mass less string and which is passing over a friction-less pulley. The tension in the string is –
(a) 3.68 N
(b) 78.4 N
(c) 26 N
(d) 13.26 N
Answer:
(c) Tension in the string T = \(\frac{2 m_{1} m_{2}}{\left(m_{1}+m_{2}\right)}\)g
T = \(\frac{2 x 2 x 4}{2 + 4}\) x 9.8 = \(\frac{16}{6}\) x 9.8 = 26.13 N
Question 97.
A bomb of 10 kg at rest explodes into two pieces of mass 4 kg and 6 kg. if the velocity of 4 kg mass is 6 ms-1 then the velocity of 6 kg is –
(a) – 4 ms-1
(b) – 6 ms-1
(c) – 24 ms-1
(d) – 2.2 ms-1
Answer:
(a) According to law of conservation of momentum
m1v1 + m2v2 = 0
v2 = –\(\frac{m_{1} v_{1}}{m_{2}}\) = \(\frac{4 x 6}{6}\) = -4ms-1
![]()
Question 98.
A body is subjected under three concurrent forces and it is in equilibrium. The resultant of any two forces is –
(a) coplanar with the third force
(b) is equal and opposite to third force
(c) both (a) and (b)
(d) none of the above
Answer:
(c) both (a) and (b)
Question 99.
An impulse is applied to a moving object with the force at an angle of 20° with respect to velocity vector. The angle between the impulse vector and the change in momentum vector is –
(a) 0°
(b) 30°
(c) 60°
(d) 120°
Answer:
(a) Impulse and change in momentum are in same direction. So the angle is zero.
Question 100.
A bullet of mass m and velocity v1 is fired into a large block of wood of mass M. The final velocity of the system is-
(a) \(\frac{v_{1}}{m+\mathrm{M}}\)
(b) \(\frac{m v_{1}}{m+\mathrm{M}}\)
(c) \(\frac{m+m}{m} v_{1}\)
(d) \(\frac{m+m}{m-M} v_{1}\)
Answer:
(b) \(\frac{m v_{1}}{m+\mathrm{M}}\)
![]()
Question 101.
A block of mass 2 kg is placed on the floor. The co – efficient of static friction is 0.4. The force of friction between the block and floor is –
(a) 2.8 N
(b) 7.8 N
(c) 2 N
(d) zero
Answer:
(b) The force required to move = = µR = µmg = 0.4 x 2 x 9.8 = 7.84 N
Question 102.
A truck weighing 1000 kg is moving with velocity of 50 km/h on smooth horizontal roads. A mass of 250 kg is dropped into it. The velocity with which it moves now is –
(a) 12.5 km/h
(b) 20 km/h
(c) 40 km/h
(d) 50 km/h
Answer:
(c) According to law of conservation of linear momentum
m2 v2 = (m1 + m2)v2
v2 = \(\frac{m_{1} v_{1}}{m_{1}+m_{2}}\) = \(\frac{1000 \times 50}{1250}\) = 40 km/h
Question 103.
A body of mass loo g is sliding from an inclined plane of inclination 30°. if u = 1.7, then the frictional force experienced is –
(a) \(\frac{3.4}{\sqrt{3}}\)N
(b) 1.47 N
(c) \(\frac{\sqrt{3}}{3.4}\)N
(d) 1.38 N
Answer:
(b) Frictional force F = µ mg cos θ = 1.7 x 0.1 x 10 cos 30°= \(\frac{1.7}{2}\) x \(\sqrt{3}\) = 1.47 N
Samacheer Kalvi 11th Physics Laws of Motion Short Answer Questions (1 Mark)
Question 1.
A passenger sitting in a car at rest, pushes the car from within. The car doesn’t move, why?
Answer:
For motion, there should be external force.
Question 2.
Give the magnitude and directions of the net force acting on a rain drop falling with a constant speed.
Answer:
as \(\overline{\mathrm{a}}\) = 0 so \(\overline{\mathrm{F}}\) = 0.
Question 3.
Why the passengers in a moving car are thrown outwards when it suddenly takes a turn?
Answer:
Due to inertia of direction.
Question 4.
You accelerate your car forward. What is the direction of the frictional force on a package resting on the floor of the car?
Answer:
The package in the accelerated car (a non inertial frame) experiences a Pseudo force in a direction opposite to that of the motion of the car. The frictional force on the package which acts opposite to this pseudo force is thus in the same direction (forward) as that of the car.
![]()
Question 5.
What is the purpose of using shockers in a car?
Answer:
To decrease the impact of force by increasing the time for which force acts.
Question 6.
Why are types made of rubber not of steel?
Answer:
Since coefficient of friction between rubber and road is less than the coefficient of friction between steel and road.
Question 7.
Wheels are made circular. Why?
Answer:
Rolling friction is less than sliding friction.
Question 8.
If a ball is thrown up in a moving train, it comes back to the thrower’s hands. Why?
Answer:
Both during its upward and downward motion, the ball continues to move inertia of motion with the same horizontal velocity as the train. In this period, the ball covers the same horizontal distance as the train and so it comes back to the thrower’s hand.
Question 9.
Calculate the force acting on a body which changes the momentum of the body at the rate of 1 kg-m/s2 .
Answer:
As F = rate change of momentum
F = 1 kg-m/s2 = 1N
![]()
Question 10.
On a rainy day skidding takes place along a curved path. Why?
Answer:
As the friction between the types and road reduces on a rainy day.
Question 11.
Why does a gun recoils when a bullet is being fired?
Answer:
To conserve momentum.
Question 12.
Why is it difficult to catch a cricket ball than a tennis ball even when both are moving with the same velocity?
Answer:
Being heavier, cricket ball has higher rate of change of momentum during motion so more force sumed.
Question 13.
The distance travelled by a moving body is directly proportional to time. Is any external force acting on it?
Answer:
As s ∝ t, so acceleration a = 0, therefore, no external force is acting on the body.
Question 14.
Calculate the impulse necessary to stop a 1500 kg car moving at a speed of 25 ms-1.
Answer:
Use formula I = change in momentum = m(v – u) (Impulse – 37500 Ns)
Question 15.
Lubricants are used between the two parts of a machine. Why?
Answer:
To reduce friction and so to reduce wear and tear.
Question 16.
What provides the centripetal force to a car taking a turn on a level road?
Answer:
Force of friction between the type and road provides centripetal force.
Question 17.
A body is acted upon by a number of external forces. Can it remain at rest?
Answer:
Yes, if the external forces acting on the body can be represented in magnitude and direction by the sides of a closed polygon taken in the same order.
Question 18.
Bodies of larger mass need greater initial effort to put them in motion. Why?
Answer:
As F = ma so for given a, more force will be required to put a large mass in motion.
![]()
Question 19.
An athlete runs a certain distance before taking a long jump Why?
Answer:
So that inertia of motion may help him in his muscular efforts to take a longer jump.
Question 20.
Action and reaction forces do not balance each other. Why?
Answer:
As they acts on different bodies.
Question 21.
The wheels of vehicles are provided with mudguards. Why?
Answer:
When the wheel rotates at a high speed, the mud sticking to the wheel flies off tangentially, this is due to inertia of direction. If order that the flying mud does not spoil the clothes of passer by the wheels are provided with mudguards.
Question 22.
China wares are wrapped in straw paper before packing. Why?
Answer:
The straw paper between the China ware increases the Time of experiencing the jerk during transportation. Hence impact of force reduces on China wares.
![]()
Question 23.
Why is it difficult to walk on a sand?
Answer:
Less reaction force.
Question 24.
The outer edge of a curved road is generally raised over the inner edge Why?
Answer:
In addition to the frictional force, a component of reaction force also provides centripetal force.
Question 25.
Explain why the water doesn’t fall even at the top of the circle when the bucket full of water is upside down rotating in a vertical circle?
Answer:
Weight of the water and bucket is used up in providing the necessary centripetal force at the top of the circle.
Question 26.
Why does a speedy motor cyclist bends towards the center of a circular path while taking a turn on it?
Answer:
So that in addition of the frictional force, the horizontal component of the normal reaction also provides the necessary centripetal forces.
Question 27.
An impulse is applied to a moving object with a force at an angle of 20° wr.t. velocity vector, what is the angle between the impulse vector and change in momentum vector ?
Answer:
Impulse and change in momentum are along the same direction. Therefore angle between these two vectors is zero.
Samacheer Kalvi 11th Physics Laws of Motion Short Answer Questions (2 Marks)
Question 28.
A man getting out of a moving bus runs in the same direction for a certain distance. Comment.
Answer:
Due to inertia of motion.
Question 29.
If the net force acting upon the particle is zero, show that its linear momentum remains constant.
Answer:
As F x \(\frac {dp}{dt}\)
when F = 0, \(\frac {dp}{dt}\) = 0 so P = constant
![]()
Question 30.
A force of 36 dynes is inclined to the horizontal at an angle of 60°. Find the acceleration in a mass of 18 g that moves in a horizontal direction.
Answer:
F = 36 dyne at an angle of 60°
Fx = F cos 60° = 18 dyne
Fx = max
So ax = \(\frac{F_{x}}{m}\) = 1 cm /s2
Question 31.
The motion of a particle of mass m is described by h = ut + \(\frac {1}{2}\) gt2. Find the force acting on particle.
Answer:
a = ut + \(\frac {1}{2}\) gt2
find a by differentiating h twice w.r.t.
a = g
As F = ma so F = mg (answer)
Question 32.
A particle of mass 0.3 kg is subjected to a force of F = -kx with k= 15 Nmr-1. What will be its initial acceleration if it is released from a point 20 cm away from the origin?
Answer:
As F = ma so F = -kx = ma
a = \(\frac {-kx}{m}\)
for x = 20 cm, ⇒ a = -10 m/s2.
![]()
Question 33.
A 50 g bullet is fired from a 10 kg gun with a speed of 500 ms-1. What is the speed of the recoil of the gun?
Answer:
Initial momentum = 0
Using conservation of linear momentum mv + MV = 0
V = \(\frac {-mv}{M}\) ⇒ V = 2.5 m/s
Question 34.
Smooth block is released at rest on a 45° incline and then slides a distance d. If the time taken of slide on rough incline is n times as large as that to slide than on a smooth incline. Show that coefficient of friction, µ = \(\left(1-\frac{1}{n^{2}}\right)\)
Answer:
When there is no friction, the block slides down the inclined plane with acceleration. a = g sin θ
when there is friction, the downward acceleration of the block is a’ = g (sin θ – µ cos θ)
As the block Slides a distance d in each case so
d = \(\frac {1}{2}\) at2 = \(\frac {1}{2}\) a’t’2
\(\frac{a}{a^{\prime}}=\frac{t^{\prime 2}}{t^{2}}=\frac{(n t)^{2}}{t^{2}}\) = n2
or \(\frac {g sin θ}{g(sin θ – µ cos θ)}\) = n2
Solving, we get (Using θ = 45°)
µ = 1 – \(\frac{1}{n^{2}}\)
![]()
Question 35.
A spring balance is attached to the ceiling of a lift. When the lift is at rest spring balance reads 49 N of a body hang on it. If the lift moves:
- Downward
- upward, with an acceleration of 5 ms2
- with a constant velocity.
What will be the reading of the balance in each case?
Answer:
1. R = m(g – a) = 49 N
so = m = \(\frac {49}{9.8}\) = 5 kg
R = 5 (9.8 – 5)
R = 24 N
2. R = m(g + a)
R = 5 (9.8 + 5)
R = 74 N
3. as a = 0 so R = mg = 49 N
Question 36.
A bob of mass 0.1 kg hung from the ceiling of room by a string 2 m long is oscillating. At its mean position the speed of a bob is 1 ms-1. What is the trajectory of the ‘oscillating bob if the string is cut when the bob is –
- At the mean position
- At its extreme position.
Answer:
- Parabolic
- vertically downwards
Question 37.
A block placed on a rough horizontal surface is pulled by a horizontal force F. Let f be the force applied by the rough surface on the block. Plot a graph of f versus F.
Answer:
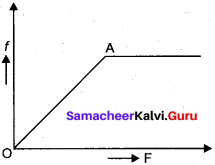
Unto point A, f = F (50 Long as block is stationary) beyond A, when F increases, block starts moving f remains constant.
Question 38.
A mass of 2 kg is suspended with thread AB. Thread CD of the same type is attached to the other end of 2 kg mass.
- Lower end of the lower thread is pulled gradually, hander and hander is the downward direction so as to apply force on AB Which of the thread will break & why?
- If the lower thread is pulled with a jerk, what happens?
Answer:
- Thread AB breaks down
- CD will break.
![]()
Question 39.
A block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is p and the acceleration due to gravity is g, calculate the minimum force required to be applied by the finger to held the block against the wall?
Answer:
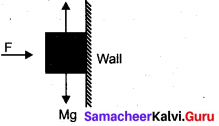
For the block not to fall f = Mg
But f = µR = µF so
µF = Mg
F = \(\frac {Mg}{µ}\)
Samacheer Kalvi 11th Physics Laws of Motion Short Answer Questions (3 Marks) & Numericals
Question 40.
A block of mass 500 g is at rest on a horizontal table. What steady force is required to give the block a velocity of 200 cm s-2 in 4 s?
Answer:
Use F – ma
a = \(\frac {v – u}{ t }\) = \(\frac {200- 0}{ 4 }\) = 50 cm/s2
F = 500 x 50 = 25,000 dyne.
Question 41.
A force of 98 N is just required to move a mass of 45 kg on a rough horizontal surface. Find the coefficient of friction and angle of friction?
Answer:
F = 48 N,R = 45 x 9.8 = 441 N
µ = \(\frac {F’}{ R}\) = 0.22
Angle of friction θ = tan-1 0.22 = 12°24′
Question 42.
Calculate the force required to move a train of 2000 quintal up on an incline plane of 1 in 50 with an acceleration of 2 ms-2. The force of friction per quintal is 0.5 N.
Answer:
Force of friction = 0.5 N per quintal
f = 0.5 x 2000 = 1000 N
m = 2000 quintals = 2000 x 100 kg
sin θ = \(\frac {1}{50}\), a – 2 m/s2
In moving up an inclined plane, force required against gravity
mg sin θ = 39200 N
And force required to produce acceleration = ma
= 2000 x 100 x 2 = 40,0000 N
Total force required = 1000 + 39,200 + 40,0000 = 440200 N.
![]()
Question 43.
A force of 100 N gives a mass m1, an acceleration of 10 ms-2 and of 20 ms-2 to a mass m2.
What acceleration must be given to it if both the masses are tied together?
Answer:
Suppose, a = acceleration produced if m1 and m2 are tied together,
F = 100 N
Let a1 and a2 be the acceleration produced in m1 and m2 respectively.
∴ a1 and a2 = 20ms-2 (given)
Again m1 = \(\frac{\mathrm{F}}{a_{1}}\) and m2 = \(\frac{\mathrm{F}}{a_{2}}\)
⇒ m1 = \(\frac {100}{10}\) = 10kg
and m2 = \(\frac {100}{20}\) = 5kg
∴ m1 + m2 = 10 + 5 = 15
so, a = \(\frac{\mathbf{F}}{m_{1}+m_{2}}\) = \(\frac {100}{15}\) = \(\frac {20}{3}\) = 6.67 ms2
Question 44.
The pulley arrangement of figure are identical. The mass of the rope is negligible. In (a) mass m is lifted up by attaching a mass (2m) to the other end of the rope. In (b), m is lifted up by pulling the other end of the rope with a constant downward force F = 2 mg. In which case, the acceleration of m is more?
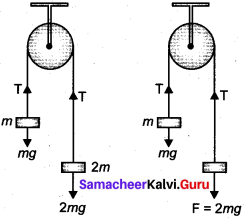
Answer:
Case (a):
a = \(\frac {2m – m}{2m + m}\) g = a = \(\frac {g}{3}\)
Case (b):
FBD of mass m
ma’ = T – mg
ma’ = 2 mg – mg
⇒ ma’ = mg
a’ = g
So in case (b) acceleration of m is more.
Question 45.
Figure shows the position-time graph of a particle of mass 4 kg. What is the
(a) Force on the particle for t < 0, t > 4s, 0 < t < 4s?
(b) Impulse at t = 0 and t = 4s?
(Consider one dimensional motion only)
Answer:
(a) For t < 0. No force as Particles is at rest. For t > 4s, No force again particle comes at rest.
For 0 < t < 4s, as slope of OA is constant so velocity constant i.e., a = 0, so force must be zero.
(b) Impulse at t = 0
Impulse = change in momentum
I = m(v – w) = 4(0 – 0.75) = 3 kg ms-1
Impulse at t = 4s
1 = m(v – u) = 4 (0 – 0.75) = -3 kg ms-1
![]()
Question 46.
What is the acceleration of the block and trolley system as the figure, if the coefficient of kinetic friction between the trolley and the surface is 0.04? Also Calculate friction in the string: Take g = 10 m/s2, mass of the string is negligible.
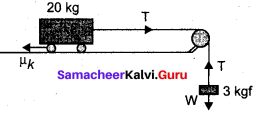
Answer:
Free body diagram of the block
30 – T = 3a
Free body diagram of the trolley
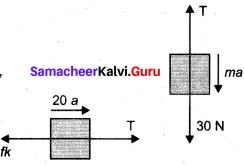
T – fk = 20 a ………….(2)
where fk = µk= 0.04 x 20 x 10 = 8 N
Solving (i) & (ii), a = 0.96 m/s2 and T = 27.2 N
Question 47.
Three blocks of masses ml = 10 kg, m2 = 20 kg are connected by strings on smooth horizontal surface and pulled by a force of 60 N. Find the acceleration of the system and frictions in the string.

Solution:
All the blocks more with common acceleration a under the force F = 60 N.
F = (m1 + m2 + m3)a
a = \(\frac{\mathrm{F}}{\left(m_{1}+m_{2}+m_{3}\right)}\) = 1 m/s2
to determine, T1 →Free body diagram of m1.
T1 = m1a = 10 x 1 = 10 N
to determine, T2 →Free body diagram of m3
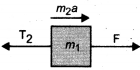
F – T2 = m3a
Solving, we get T2 = 30 N
![]()
Question 48.
The rear side of a truck is open and a box of 40 kg mass is placed 5m away from the open end. The coefficient of friction between the box and the surface below it is 0.15 on a straight road, the truck starts from rest and accelerates with 2 m/s2. At what distance from the starting point does the box fall off the truck ? (ignore the size of the box)
Answer:
Force on the box due to accelerated motion of the truck
F = ma = 40 x 2 = 80 N (in forward direction)
Reaction on the box, F’ = F = 80 N (in backward direction)
Force of limiting friction, f = µR = 0 .15 x 40 x 10 = 60 N
Net force on the box in backward direction is P = F’ f = 80 – 60 = 20 N
Backward acceleration in the box = a= \(\frac {p}{m}\) = \(\frac {20}{40}\) = 0.5 ms-2
t = time taken by the box to travel s = 5 m and falls off the truck, then from
s = ut + \(\frac {1}{2}\) at2
5 = 0 x t + \(\frac {1}{2}\) x 0.5 x t2
t = 4.47
If the truck travels a distance x during this time
then x = 0 x 4.34 +\(\frac {1}{2}\) x 2 x (4.471)2
x = 19.98 m
Question 49.
A block slides down as incline of 30° with the horizontal. Starting from rest, it covers 8 m in the first 2 seconds. Find the coefficient of static friction.
Use s = ut + \(\frac {1}{2}\) at2
a = \(\frac{2 s}{t^{2}}\) at2 as u = 0
µ = \(\frac{g sin θ – a}{g Cos θ }\)
Putting the value and solving, µ = 0.11
Question 50.
A helicopter of mass 2000 kg rises with a vertical acceleration of 15 m/s2 . The total mass of the crew and passengers is 500 kg. Give the magnitude and direction of the:
(a) Force on the floor of the helicopter by the crew and passenger.
(b) Action of the rotor of the helicopter on the surrounding air
(c) Force on the helicopter due to the surrounding air (g = 10 m/s2 )
Answer:
(a) Force on the floor of the helicopter by the crew and passengers
= apparent weight of crew and passengers
= 500(10+ 15)
=12500 N
(b) Action of rotor of helicopter on surrounding air is Obviously vertically downwards, because helicopter rises on account of reaction of this force. Thus force of action
= (2000 + 500) (10 + 15)
= 2500 x 25
= 62,500 N
(c) Force on the helicopter due to surrounding air is obviously a reaction. As action and reaction are equal and opposite, therefore
Force of reaction F’ = 62,500 vertically upwards.
![]()
Question 51.
A rectangular box lies on a rough inclined surface. The coefficient of friction between the surface and the box is (µ). Let the mass of the box be m.
- At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
- What is the force acting on the box down the plane, if the angle of inclination of the plane is increased to a > θ.
- What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed ?
- What is the force needed to be applied upwards along the plane to pk kg f make the box move up the plane with acceleration a ?
Answer:
1. When the box just starts sliding
µ = tanθ
or 0 = tan-1 µ
2. Force acting on the box down the plane
= mg (sin a – µ cos a)
3. Force needed mg (sin a + µ cos a)
4. Force needed = mg (sin a + µ cos a) + ma.
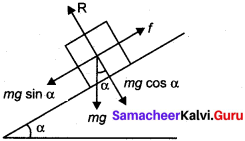
Question 52.
Two masses of 5 kg and 3 kg are suspended with help of mass less in extensible string as shown. Calculate T1 and T2 when system is going upwards with acceleration m/s2. (Use g 9.8 m/s2)
Answer:
According Newton’s second law of motion
(1) T1 – (m1 + m2)g = (m1 + m2)a
T1 = (m1 + m2)(a + g) = (5 + 3) (2 + 9.8)
T1 = 94.4 N
(2) T2 – m2g = m2a
T2 = m2 (a + g)
T2 = 3(2 + 9.8)
T2 = 35.4 N
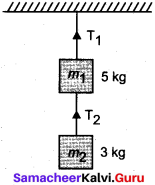
Question 53.
There are few forces acting at a Point P produced by strings as shown, which is at rest. Find the forces F1 & F1
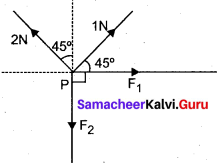
Answer:
Using Resolution of forces IN and 2N and then applying laws of vector addition. Calculate for F1 & F1.
F1 = \(\frac{1}{\sqrt{2}}\) N, F2 = \(\frac{3}{\sqrt{2}}\)N
Question 54.
A hunter has a machine gun that can fire 50g bullets with a velocity of 150 ms A 60 kg tiger springs at him with a velocity of 10 ms-1. How many bullets must the hunter fire into the target so as to stop him in his track?
Answer:
Given m = mass of bullet = 50 gm = 0.50 kg
M = mass of tiger = 60 kg
v = Velocity of bullet – 150 m/s
V = Velocity of tiger = – 10 m/s
(v It is coming from opposite direction n = no. of bullets fired per second at the tiger so as to stop it.)
Pi = 0, before firing ……..(i)
Pf = n (mv) + MV …………(ii)
∴ From the law of conservation of momentum,
Pi = Pf
⇒ 0 = n (mv) + MV
n = \(\frac{MV}{mv}\) = \(\frac{-60 \times(-10)}{0.05 \times 150}\) = 80
![]()
Question 55.
Two blocks of mass 2 kg and 5 kg are connected by an ideal string passing over a pulley. The block of mass 2 kg is free to slide on a surface inclined at an angle of 30° with the horizontal whereas 5 kg block hangs freely. Find the acceleration of the system and the tension in the string.
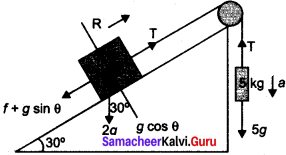
Let a be the acceleration of the system and T be the Tension in the string. Equations of motions for 5 kg and 2 kg blocks are
5g – T = 5a
T – 2g sin θ – f = 2a
where f = force of limiting friction
= µR = µ mg cos θ = 0.3 x 2 g x cos 30°
Solving (1) & (2)
a = 4.87 m/s2