Samacheer Kalvi 11th Physics Solutions Chapter 2 Kinematics

Students can Download Physics Chapter 2 Kinematics Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Physics Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Physics Solutions Chapter 2 Kinematics

Samacheer Kalvi 11th Physics Kinematics Textual Questions Solved

Samacheer Kalvi 11th Physics Kinematics Multiple Choice Questions

Question 1.
Which one of the following Cartesian coordinate systems is not followed in physics?

Answer:

Question 2.
Identify the unit vector in the following:
(a) \(\hat{i}+\hat{j}\)
(b) \(\frac{\hat{i}}{\sqrt{2}}\)
(c) \(\hat{k}-\frac{\hat{j}}{\sqrt{2}}\)
(d) \(\frac{\hat{i}+\hat{j}}{\sqrt{2}}\)
Answer:
(d) \(\frac{\hat{i}+\hat{j}}{\sqrt{2}}\)

online acceleration calculator tool makes the calculation faster, and it displays the acceleration of the object in a fraction of seconds.

Question 3.
Which one of the following physical quantities cannot be represented by a scalar?
(a) Mass
(b) length
(c) momentum
(d) magnitude of acceleration
Answer:
(c) momentum

Question 4.
Two objects of masses m₁ and m₂, fall from the heights h₁ and h₂ respectively. The ratio of the magnitude of their momenta when they hit the ground is [AIPMT 20121]
(a) \(\sqrt{\frac{h_{1}}{h_{2}}}\)
(b) \(\sqrt{\frac{m_{1} h_{1}}{m_{2} h_{2}}}\)
(c) \(\frac{m_{1}}{m_{2}} \sqrt{\frac{h_{1}}{h_{2}}}\)
(d) \(\frac{m_{1}}{m_{2}}\)
Answer:
(c) \(\frac{m_{1}}{m_{2}} \sqrt{\frac{h_{1}}{h_{2}}}\)

Question 5.
If a particle has negative velocity and negative acceleration, its speed
(a) increases
(b) decreases
(c) remains same
(d) zero
Answer:
(a) increases

Question 6.
If the velocity is\(\overrightarrow{\mathrm{v}}\) – 2\(\hat{i}\) +t²\(\hat{j}\) – 9\(\overrightarrow{\mathrm{k}}\) , then the magnitude of acceleration at t = 0.5 s is
(a) 1 m s^-2
(b) 1 m
(c) zero
(d) -1 m s s^-2
Answer:
(a) 1 m s^-2

Question 7.
If an object is dropped from the top of a building and it reaches the ground at t = 4 s, then the height of the building is (ignoring air resistance) (g = 9.8 m s^-2).
(a) 77.3 m
(b) 78.4 m
(c) 80.5 m
(d) 79.2 m
Answer:
(b) 78.4 m

Question 8.
A ball is projected vertically upwards with a velocity v. It comes back to ground in time t. Which v -1 graph shows the motion correctly?[NSEP 00 – 01]

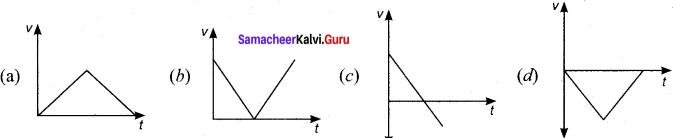
Answer:

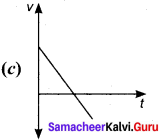
Question 9.
If one object is dropped vertically downward and another object is thrown horizontally from the same height, then the ratio of vertical distance covered by both objects at any instant is
(a) 1
(b) 2
(c) 4
(d) 0.5
Answer:
(a) 1

Question 10.
A ball is dropped from some height towards the ground. Which one of the following represents the correct motion of the ball?

Answer:

Question 11.
If a particle executes uniform circular motion in the xy plane in clockwise direction, then the angular velocity is in
(a) +y direction
(b) +z direction
(c) -z direction
(d) -x direction
Answer:
(c) -z direction

Question 12.
If a particle executes uniform circular motion, choose the correct statement [NEET 2016]
(a) The velocity and speed are constant.
(b) The acceleration and speed are constant.
(c) The velocity and acceleration are constant.
(d) The speed and magnitude of acceleration are constant.
Answer:
(d) The speed and magnitude of acceleration are constant.

Question 13.
If an object is thrown vertically up with the initial speed u from the ground, then the time taken by the object to return back to ground is
(a) \(\frac{u^{2}}{2 g}\)
(b) \(\frac{u^{2}}{g}\)
(c) \(\frac{u}{2 g}\)
(d) \(\frac{2 u}{g}\)
Answer:
(d) \(\frac{2 u}{g}\)

Question 14.
Two objects are projected at angles 30° and 60° respectively with respect to the horizontal direction. The range of two objects are denoted as R_30° and R_60°– Choose the correct relation from the following:
(a) R_30° = R_60°
(b) R_30° = 4R_60°
(c) \(\mathrm{R}_{30^{\circ}}=\frac{\mathrm{R}_{60^{\circ}}}{2}\)
(d) R_30° = 2R_60°
Answer:
(a) R_30° = R_60°

Question 15.
An object is dropped in an unknown planet from height 50 m, it reaches the ground in 2 s. The acceleration due to gravity in this unknown planet is
(a) g = 20 m s^-2
(b) g = 25 m s^-2
(c) g = 15 m s^-2
(d) g = 30 m s ^-2
Answer:
(a) g = 25 m s^-2

Samacheer Kalvi 11th Physics Kinematics Short Answer Questions

Question 1.
Explain what is meant by Cartesian coordinate system?
Answer:
At any given instant of time, the frame of reference with respect to which the position of the object is described in terms of position coordinates (x, y, z) is called Cartesian coordinate system.

Reference Angle Calculator is a free online tool that displays the reference angle for the given angle and its position.

Question 2.
Define a vector. Give examples.
Answer:
Vector is a quantity which is described by the both magnitude and direction. Geometrically a vector is directed line segment.
Example – force, velocity, displacement.

Question 3.
Define a scalar. Give examples.
Answer:
Scalar is a property which can be described only by magnitude.
Example – mass, distance, speed.

Question 4.
Write a short note on the scalar product between two vectors.
Answer:
The scalar product (or dot product) of two vectors is defined as the product of the magnitudes of both the vectors and the cosine of the angle between them. Thus if there are two vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) having an angle 0 between them, then their scalar product is defined as \(\overrightarrow{\mathrm{A}}\) • \(\overrightarrow{\mathrm{B}}\) = AB cos 0. Here, AB and are magnitudes of \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\).

Question 5.
Write a short note on vector product between two vectors.
Answer:
The vector product or cross product of two vectors is defined as another vector having a magnitude equal to the product of the magnitudes of two vectors and the sine of the angle between them. The direction of the product vector is perpendicular to the plane containing the two vectors, in accordance with the right hand screw rule or right hand thumb rule. Thus, if\(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) are two vectors, then their vector product is written as \(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) which is a vector C defined by \(\overrightarrow{\mathrm{c}}\) = \(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\) = (AB sin 0) \(\hat{n}\)
The direction \(\hat{n}\) of \(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\) , i.e., \(\overrightarrow{\mathrm{c}}\) is perpendicular to the plane containing the vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\).

Question 6.
How do you deduce that two vectors are perpendicular?
Answer:
If two vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) are perpendicular to each other than their scalar product \(\overrightarrow{\mathrm{A}}\) \(\overrightarrow{\mathrm{B}}\) = 0 because cos 90° = 0. Then he vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) are said to be mutually orthogonal.

Question 7.
Define displacement and distance.
Answer:
Distance is the actual path length traveled by an object in the given interval of time during the motion. It is a positive scalar quantity. Displacement is the difference between the final and initial positions of the object in a given interval of time. It can also be defined as the shortest distance between these two positions of the object. It is a vector quantity.

Question 8.
Define velocity and speed.
Answer:
Speed is defined as the ratio of total distance covered to the total time taken, it is a scalar quantity and always it is positive. Velocity is defined as the ratio of the displacement vector to the corresponding time interval. It is a vector quantity or it can also be defined as rate of change of displacement.

Question 9.
Define acceleration.
Answer:
Acceleration of a particle is defined as the rate of change of velocity or it can also be defined as the ratio of change in velocity to the given interval of time.

The Average Velocity calculator computes the velocity (V) based on the change in position (Δx) and the change in time (Δt).

Question 10.
What is the difference between velocity and average velocity.
Answer:

Question 11.
Define a radian?
One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle.
1 rad = 57.295°

Question 12.
Define angular displacement and angular velocity.
Answer:
1. Angular displacement:
The angle described by the particle about the axis of rotation in a given time is called angular displacement.

2. Angular velocity:
The rate of change of angular displacement is called angular velocity.

Question 13.
What is non uniform circular motion?
If the speed of the object in circular motion is not constant, then we have non-uniform circular motion. For example, when the bob attached to a string moves in vertical circle, the speed of the bob is not the same at all time Whenever the speed is not same in circular motion, the particle will have both centripetal and tangential acceleration.

Question 14.
Write down the kinematic equations for angular motion.
Answer:
Kinematic equations for circular motion are –

1. \(\omega=\omega_{0}+\alpha t\)
2. \(\theta=\omega_{0} t+\frac{1}{2} \alpha t^{2}\)
3. \(\omega^{2}=\omega_{o}^{2}+2 \alpha \theta\)
4. \(\theta=\frac{\left(\omega_{0}+\omega\right)}{2} t\)

Here,
ω₀  = initial angular velocity
ω = final angular velocity
θ = angular displacement
α = angular acceleration
t = time.

Question 15.
Write down the expression for angle made by resultant acceleration and radius vector in the non uniform circular motion.
Answer:
The angle made by resultant acceleration and radius vector in the non uniform circular motion is –
\(\tan \theta=\frac{a_{t}}{\left(\frac{V^{2}}{r}\right)}\) or \(\theta=\tan ^{-1}\left(\frac{a_{t}}{\left(\frac{V^{2}}{r}\right)}\right)\)

Samacheer Kalvi 11th Physics Kinematics Long Answer Questions

Question 1.
Explain in detail the triangle law of addition.
Answer:
Let us consider two vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) as shown in figure. To find the resultant of the two vectors we apply the triangular.

Law of addition as follows:
present the vectors A and by the two adjacent sides of a triangle taken in the same order. Then the resultant is given by the third side of the triangle as shown in figure.


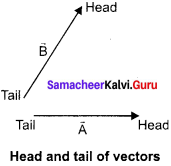
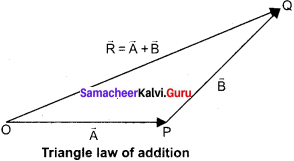
To explain further, the head of the first vector \(\overrightarrow{\mathrm{A}}\) is connected to the tail of the second vect \(\overrightarrow{\mathrm{B}}\) Let O he the angle between\(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\). Then \(\overrightarrow{\mathrm{R}}\) is the resultant vector connecting the tail of the first vector \(\overrightarrow{\mathrm{A}}\) to the head of the second vector \(\overrightarrow{\mathrm{B}}\) The magnitude of \(\overrightarrow{\mathrm{R}}\). (resultant) given geometrically by the length of (OQ) and the direction of the resultant vector is the angle between \(\overrightarrow{\mathrm{R}}\). and \(\overrightarrow{\mathrm{A}}\). Thus we write
\(\overrightarrow{\mathrm{R}}\) = \(\overrightarrow{\mathrm{A}}\) +\(\overrightarrow{\mathrm{B}}\) \(\overrightarrow{\mathrm{OQ}}\) = \(\overrightarrow{\mathrm{OP}}\) + \(\overrightarrow{\mathrm{PQ}}\)

1. Magnitude of resultant vector:
The magnitude and angle of the resultant vector ar determined by using triangle law of vectors as follows.From figure, consider the triangle ABN, which is obtained by extending the side OA to ON. ABN is a right angled triangle.

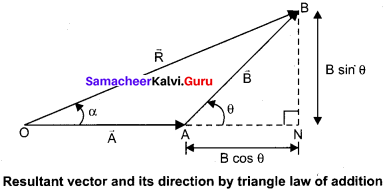
From figure, let R is the magnitude of the resultant of \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\).
cos θ = \(\frac { AN}{ B }\) ∴ AN = B cos θ and sinθ = \(\frac { BN}{ B }\) ∴BN = B sinθ
For ∆ OBN, we have OB² = ON² + BN²
⇒ R² = (A + B cos θ)² + (B sinθ)²
⇒ R² = A² + B² cos²θ + 2ABcosθ B² sin²θ
⇒ R² = A² + B²(cos²θ + sin²θ) + 2AB cos θ
⇒ R² = \(\sqrt{A^{2}+B^{2}+2 A B \cos \theta}\)

2. Direction of resultant vectors:
If 0 is the angle between \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) then,
\(|\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}|=\sqrt{\mathrm{A}^{2}+\mathrm{B}^{2}+2 \mathrm{AB} \cos \theta}\)
If R makes an angle α with \(\overrightarrow{\mathrm{A}}\) , then in AOBN,
tan α = \(\frac { BN}{ ON }\) = \(\frac { BN}{ OA + AN }\)
tan α = \(\frac { B sinθ }{ A + B cosθ}\) ⇒ α = \(\tan ^{-1}\left(\frac{B \sin \theta}{A+B \cos \theta}\right)\)

Question 2.
Discuss the properties of scalar and vector products.
Answer:
Properties of scalar product of two vectors are:
(1) The product quantity \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{B}}\) is always a scalar. It is positive if the angle between the vectors is acute (i.e., < 90°) and negative if the angle between them is obtuse (i.e. 90°<0< 180°).

(2) The scalar product is commutative, i.e. \(\overrightarrow{\mathrm{A}}\) \(\overrightarrow{\mathrm{B}}\) ≠ \(\overrightarrow{\mathrm{B}}\). \(\overrightarrow{\mathrm{A}}\)

(3) The vectors obey distributive law i.e. \(\overrightarrow{\mathrm{A}}\)(\(\overrightarrow{\mathrm{B}}\) + \(\overrightarrow{\mathrm{C}}\)) = \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{B}}\) + \(\overrightarrow{\mathrm{A}}\) .\(\overrightarrow{\mathrm{C}}\)
(4) The angle between the vectors θ = \(\cos ^{-1}\left[\frac{\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}}{\mathrm{AB}}\right]\)

(5) The scalar product of two vectors will be maximum when cos θ = 1, i.e. θ = 0°, i.e., when the vectors are parallel;
\((\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}})_{\max }=\mathrm{AB}\)

(6) The scalar product of two vectors will be minimum, when cos θ = -1, i.e. θ = 180°.
\((\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}})_{\min }=-\mathrm{AB}\) when the vectors are anti-parallel.

(7) If two vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) are perpendicular to each other than their scalar product \(\overrightarrow{\mathrm{A}}\) .\(\overrightarrow{\mathrm{B}}\) = 0, because cos 90° 0. Then the vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) are said to be mutually orthogonal.

(8) The scalar product of a vector with itself is termed as self-dot product and is given by (\(\overrightarrow{\mathrm{A}}\))² = \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{A}}\) = AA cos 0 = A². Here angle 0 = 0°.
The magnitude or norm of the vector \(\overrightarrow{\mathrm{A}}\) is |\(\overrightarrow{\mathrm{A}}\)| = A = \(\sqrt{\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{A}}}\).

(9) In case of a unit vector \(\hat{n}\)
\(\hat{n}\) . \(\hat{n}\) = 1 x 1 x cos 0 = 1. For example, \(\hat{i}\) – \(\hat{i}\) = \(\hat{j}\) . \(\hat{j}\) = \(\hat{k}\) . \(\hat{k}\) = 1.

(10) In the case of orthogonal unit vectors, \(\hat{i}\),\(\hat{j}\) and \(\hat{k}\),
\(\hat{i}\) . \(\hat{j}\) = \(\hat{j}\).\(\hat{k}\) = \(\hat{k}\) . \(\hat{i}\)= 1.1 cos 90° = 0

(11) In terms of components the scalar product of \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) can be written as
\(\overrightarrow{\mathrm{A}}\).\(\overrightarrow{\mathrm{B}}\) = (A_x\(\hat{i}\) + A_y\(\hat{j}\) + A_z\(\hat{k}\)).(B_x\(\hat{i}\) + B_y\(\hat{j}\) + B_z\(\hat{k}\))
= A _xB_x + A_yB_y+ A_zB_z, with all other terms zero.
The magnitude of vector | \(\overrightarrow{\mathrm{A}}\) | is given by
| \(\overrightarrow{\mathrm{A}}\) | = A = \(\sqrt{\mathrm{A}_{x}^{2}+\mathrm{A}_{y}^{2}+\mathrm{A}_{z}^{2}}\)

Properties of vector product of two vectors are:
(1) The vector product of any two vectors is always another vector whose direction is perpendicular to the plane containing these two vectors, i.e., orthogonal to both the vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\), even though the vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) may or may not be mutually orthogonal.

(2) The vector product of two vectors is not commutative, i.e., \(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\) ≠ \(\overrightarrow{\mathrm{B}}\) x \(\overrightarrow{\mathrm{A}}\). But,
\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\)=-\(\overrightarrow{\mathrm{B}}\) x \(\overrightarrow{\mathrm{A}}\).
Here it is worthwhile to note that |\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\)| =
|\(\overrightarrow{\mathrm{B}}\) x \(\overrightarrow{\mathrm{A}}\)| = AB sin 0 i.e., in the case of the product vectors \(\overrightarrow{\mathrm{B}}\)=-\(\overrightarrow{\mathrm{B}}\) and \(\overrightarrow{\mathrm{B}}\) x \(\overrightarrow{\mathrm{A}}\), the magnitudes are equal but directions are opposite to each other.

(3) The vector product of two vectors will have maximum magnitude when sin 0 = 1, i.e., 0 = 90° i.e., when the vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) are orthogonal to each other.
\((\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}})_{\mathrm{max}}=\mathrm{AB} \hat{n}\) = AB \(\hat{n}\)

(4) The vector product of two non-zero vectors will be minimum when sin θ = 0, i.e θ = 0° or 180°
\((\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}})_{\min }=0\)
i. e., the vector product of two non – zero vectors vanishes, if the vectors are either parallel or anti parallel.

(5) The self – cross product, i.e., product of a vector with itself is the null vector
\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{A}}\) = AA sin 0° \(\hat{n}\) = \(\overrightarrow{\mathrm{0}}\) In physics the null vector 0 is simply denoted as zero.

(6) The self – vector products of unit vectors are thus zero.
\(\hat{i}\) x \(\hat{i}\) = \(\hat{ j}\) x \(\hat{j}\) = \(\hat{k}\) x \(\hat{k}\) = 0

(7) In the case of orthogonal unit vectors, \(\hat{i}\), \(\hat{j}\). \(\hat{k}\) , in accordance with the right hand screw rule:
\(\hat{i}\) x \(\hat{j}\) = \(\hat{k}\), \(\hat{j}\) x \(\hat{k}\) = \(\hat{i}\) and \(\hat{k}\) x \(\hat{i}\) = \(\hat{j}\)

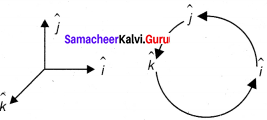
Also, since the cross product is not commutative,
\(\hat{j}\) x \(\hat{i}\) = –\(\hat{k}\), \(\hat{k}\) x \(\hat{j}\) = –\(\hat{i}\) and \(\hat{i}\) x \(\hat{k}\) = \(\hat{j}\)

(8) In terms of components, the vector product of two vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) is –

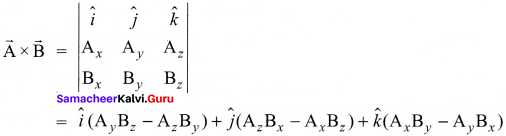
Note that in the \(\hat{j}^{\mathrm{th}}\) component the order of multiplication is different than \(\hat{i}^{\mathrm{th}}\) and \(\hat{k}^{\mathrm{th}}\) components.

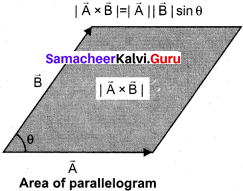
(9) If two vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) form adjacent sides in a parallelogram, then the magnitude of |\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\)| will give the area of the parallelogram as represented graphically in figure.

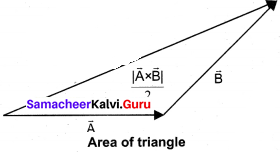
(10) Since we can divide a parallelogram into two equal triangles as shown in the figure, the area of a triangle with \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) as sides is \(\frac { 1 }{ 2 }\) |\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\)| . This is shown in the Figure. A number of quantities used in Physics are defined through vector products. Particularly physical quantities representing rotational effects like torque, angular momentum, are defined through vector products.

Question 3.
Derive the kinematic equations of motion for constant acceleration.
Answer:
Consider an object moving in a straight line with uniform or constant acceleration ‘a’. Let u be the velocity of the object at time t = 0, and v be velocity of the body at a later time t.

Velocity – time relation:
(1) The acceleration of the body at any instant is given by the first derivative of the velocity with respect to time,
a = \(\frac {dv}{dt}\) or dv = a dt
Integrating both sides with the condition that as time changes from 0 to t, the velocity changes from u to v. For the constant acceleration,

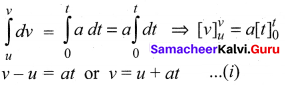
(2) The velocity of the body is given by the first derivative of the displacement with respect to time.
v = \(\frac {ds}{dt}\) or ds = vdt
and since v = u + at,
we get ds = (u+ at ) dt
Assume that initially at time t = 0, the particle started from the origin. At a later time t, the particle displacement is s. Further assuming that acceleration is time-independent, we have

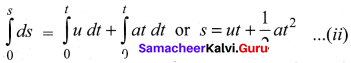
Velocity – displacement relation:

(3) The acceleration is given by the first derivative of velocity with respect to time.
a = \(\frac {dv}{dt}\) = \(\frac {dv}{ds}\) = \(\frac {ds}{dt}\) = \(\frac {dv}{ds}\) v [since ds/dt = v] where s is displacement traverse
This is rewritten as a = \(\frac{1}{2} \frac{d v^{2}}{d s}\) or ds = \(\frac{1}{2 a} d\left(v^{2}\right)\) Integrating the above equation, using the fact when the velocity changes from u² to v², displacement changes from 0 to s, we get

We can also derive the displacement 5 in terms of initial velocity u and final velocity v. From equation we can
write,
at = v – u
Substitute this in equation, we get

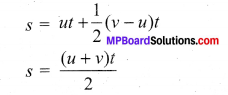
Question 4.
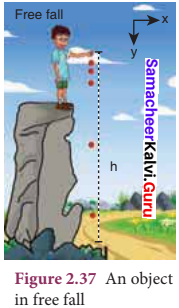
Derive the equations of motion for a particle (a) falling vertically (b) projected vertically.
Answer:
’Equations of motion for a particle falling vertically downward from certain height. Consider an object of mass m falling from a height h. Assume there is no air resistance. For convenience, let us choose the downward direction as positive y – axis as shown in the figure. The object experiences acceleration ‘g’ due to gravity which is constant near the surface of the Earth. We can use kinematic equations to explain its motion. We have The acceleration \(\overrightarrow{\mathrm{a}}\) = g \(\hat{i}\)
By comparing the components, we get,
Equations of motion for a particle thrown vertically upwards,
a_x = 0, a_x = 0, a_y = g Let us take for simplicity, a_y = a = g

If the particle is thrown with initial velocity ‘u’ downward which is in negative y – axis, then velocity and position at of the particle any time t is given by
v = u + gt
v = ut + \(\frac {1}{2}\) – gt²
The square of the speed of the particle when it is at a distance y from the hill – top, is v² = u² + 2 gy
Suppose the particle starts from rest.
Then u = 0
Then the velocity v, the position of the particle and v² at any time t are given by (for a point y from the hill – top)
v = gt …………(i)
y = \(\frac {1}{2}\) – gt² …………(ii)
v² = 2gy …………(iii)
The time (t = T) taken by the particle to reach the ground (for which y = h), is given by using equation (ii),
h = \(\frac {1}{2}\) – gT² …………(iv)
T = \(\sqrt{\frac{2 h}{g}}\) …………(v)
The equation (iv) implies that greater the height (h), particle takes more time (T) to reach the ground. For lesser height (h), it takes lesser time to reach the ground. The speed of the particle when it reaches the ground (y = h) can be found using equation (iii), we get,
\(v_{\text {ground }}=\sqrt{2 g h}\) …………(vi)
The above equation implies that the body falling from greater height (h) will have higher velocity when it reaches the ground. The motion of a body falling towards the Earth from a small altitude (h<<R), purely under the force of gravity is called free fall. (Here R is radius of the Earth).

case (ii):
A body thrown vertically upwards:
Consider an object of mass m thrown vertically upwards with an initial velocity u. Let us neglect the air friction. In this case we choose the vertical direction as positive y axis as shown in the figure, then the acceleration a = -g (neglect air friction) and g points towards the negative y axis. The kinematic equations for this motion are,
The velocity and position of the object at any time t are,

v = u – gt ……………(vii)
s = ut – \(\frac {1}{2}\) – gt² …………..(viii)
The velocity of the object at any position y (from the point where the object is thrown) is
v² = u² – 2gy …………..(ix)

Question 5.
Derive the equation of motion, range and maximum height reached by the particle thrown at an oblique angle 9 with respect to the horizontal direction.
Answer:
This projectile motion takes place when the initial velocity is not horizontal, but at some angle with the vertical, as shown in Figure.
(Oblique projectile)
Examples:

• Water ejected out of a hose pipe held obliquely.
• Cannon fired in a battle ground.

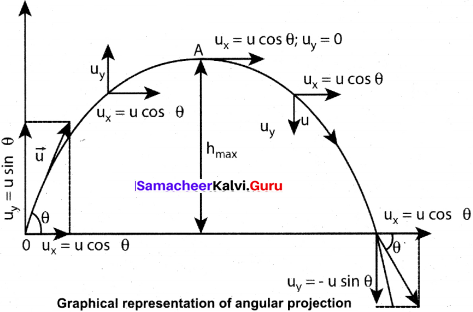
Consider an object thrown with initial velocity at an angle θ with the horizontal.
Then,
\(\overrightarrow{\mathrm{u}}\) = u_x î + u_y\(\hat{j}\) .
where u_x = u cos θ is the horizontal component and u_y = u sin θ the vertical component of velocity. Since the acceleration due to gravity is in the direction opposite to the direction of vertical component u_y , this component will gradually reduce to zero at the maximum height of the projectile. At this maximum height, the same gravitational force will push the projectile to move downward and fall to the ground. There is no acceleration along the x direction throughout the motion. So, the horizontal component of the velocity (u_x = u cos θ) remains the same till the object reaches the ground. Hence after the time t, the velocity along horizontal motion v_x = u_x + a_xt = u_x = u cos θ. The horizontal distance travelled by projectile m time t is s_x = \(u_{x} t+\frac{1}{2} a_{x} t^{2}\)
Here, s_x = x, u_x = u cos θ, a_x = 0

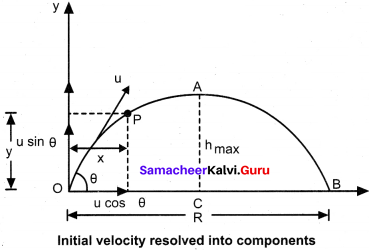
Thus, x = u cos θ or t = \(\frac {x}{u cos θ}\) ……..(i)
Next, for the vertical motion v_y= u_y + a_yt
Here u_y = u sin θ, a_y = -g (acceleration due to gravity acts opposite to the motion).
Thus, v_y= u sin θ – gt
The vertical distance traveled by the projectile in the same time t is
Here, s_y = y, u_y = u sin θ, a_x = -g. Then
y = u sinθ t – \(\frac {1}{2}\) – gt² ………..(ii)
Substitute the value of t from equation (i) in equation (ii), we have .

Thus the path followed by the projectile is an inverted parabola Maximum height (h_max): The maximum vertical distance travelled by the projectile during the journey is called maximum height. This is determined as follows:
For the vertical part of the motion.
\(v_{y}^{2}=u_{y}^{2}+2 a_{y} s\)
Here, u_y = u sin θ, a = -g, s = h_max, and at the maximum height v_y = 0
Hence, (0)² = u² sin² θ = 2 gh_max or \(h_{\max }=\frac{u^{2} \sin ^{2} \theta}{2 g}\)

Time of flight (T_f):
The total time taken by the projectile from the point of projection till it hits the horizontal plane is called time of flight. This time of flight is the time taken by the projectile to go from point O to B via point A as shown
we know that s_y = y = 0 (net displacement in y-direction is zero),
u_y = u sin θ, a_y = -g , t = T_f Then

Horizontal range (R):
The maximum horizontal distance between the point of projection and the point on the horizontal plane where the projectile hits the ground is called horizontal range (R). This is found easily since the horizontal component of initial velocity remains the same. We can write Range R = Horizontal component of velocity x time of flight = u cos θ x \(\mathrm{T}_{f}=\frac{u^{2} \sin 2 \theta}{g}\) The horizontal range directly depends on the initial speed (u) and the sine of angle of projection (θ). It inversely depends on acceleration due to gravity ‘g’.
For a given initial speed u, the maximum possible range is reached when sin 2θ is maximum, sin 2θ = 1. This implies 2θ = π/2 or θ = \(\frac {π}{4}\) This means that if the particle is projected at 45 degrees with respect to horizontal, it attains maximum range, given by.
\(\mathrm{R}_{\max }=\frac{u^{2}}{g}\) ………..(vi)

Question 6.
Derive the expression for centripetal acceleration.
Answer:
In uniform circular motion the velocity vector turns continuously without changing its magnitude (speed), as shown in figure.

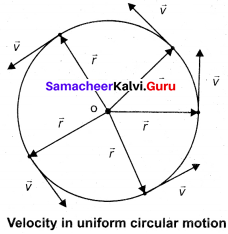
Note that the length of the velocity vector is not changed during the motion, implying that the speed remains constant. Even though the velocity is tangential at every point in the circle, the acceleration is acting towards the center of the circle. This is called centripetal acceleration. It always points towards the center of the circle. This is shown in the figure.

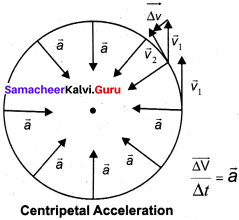
The centripetal acceleration is derived from a simple geometrical relationship between position and velocity vectors.

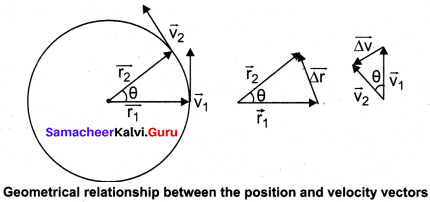
Let the directions of position and velocity vectors shift through the same angle θ in a small interval of time ∆t, as shown in figure. For uniform circular motion, r = \(\left|\vec{r}_{1}\right|\) = \(\left|\vec{r}_{2}\right|\) and v = \(\left|\vec{v}_{1}\right|\) = \(\left|\vec{v}_{2}\right|\). If the particle moves from position vector \(\vec{r}_{1}\) to \(\vec{r}_{2}\), the displacement is given by ∆\(\overrightarrow{\mathrm{r}}\) = \(\vec{r}_{2}\) – \(\vec{r}_{1}\) and the change in velocity from \(\vec{v}_{1}\) to\(\vec{v}_{2}\) is given by ∆\(\overrightarrow{\mathrm{v}}\) = \(\vec{v}_{2}\) – \(\vec{v}_{1}\),. The magnitudes of the displacement ∆r and of ∆v satisfy the following relation. \(\frac {∆r}{r}\) = \(\frac {-∆v}{v}\) = θ Here the negative sign implies that ∆v points radially inward, towards the center of the circle.

For uniform circular motion v = cor, where co is the angular velocity of the particle about center. Then the centripetal acceleration can be written as.
a = -ω²r

Question 7.
Derive the expression for total acceleration in the non uniform circular motion.
Answer:
If the speed of the object in circular motion is not constant, then we have non-uniform circular motion. For example, when the bob attached to a string moves in vertical circle, the speed of the bob is not the same at all time. Whenever the speed is not same in circular motion, the particle will have both centripetal and tangential acceleration as shown in the figure.

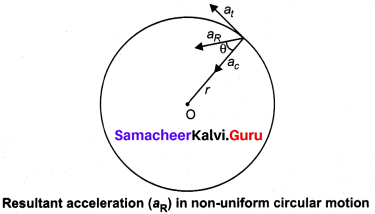
The resultant acceleration is obtained by vector sum of centripetal and tangential acceleration Since centripetal acceleration is \(\frac{v^{2}}{r}\), the magnitude of this resultant acceleration is given by –\(\dot{a}_{\mathrm{R}}=\sqrt{a_{t}^{2}+\left(\frac{v^{2}}{r}\right)^{2}}\)
This resultant acceleration makes an angle 0 with the radius vector as shown in figure.
This angle is given by tan θ = \(\frac{a_{t}}{\left(v^{2} / r\right)}\)

Samacheer Kalvi 11th Physics Kinematics Numerical Questions

Question 1.
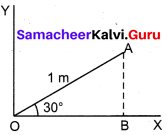
The position vector of the particle has length 1 m and makes 30° with the x-axis. What are the lengths of the x and y – components of the position vector?
Answer:
Given,
Length of position vector = 1 m
Angle made with x axis = 30
Solution:
Length of X component (OB) = OA cos θ
= 1 x cos 30°
= \(\frac{\sqrt{3}}{2}\) (or) 0.87 m
Length of Y component (AB) = OA sin θ = 1 x sin 30° = \(\frac { 1 }{ 2 }\) = 0.5 m.

Question 2.
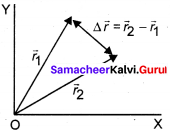
A particle has its position moved from \(\vec{r}_{1}\) = 3\(\hat{i}\) + 4\(\hat{j}\) to r2 = \(\hat{i}\) + 2\(\hat{i}\). Calculate the displacement vector (∆\(\overrightarrow{\mathrm{r}}\) ) and draw the \(\vec{r}_{1}\), \(\vec{r}_{2}\) and ∆\(\overrightarrow{\mathrm{r}}\) vector in a two dimensional Cartesian coordinate system.
Answer:
Given,
Position vectors \(\vec{r}_{1}\) = 3\(\hat{i}\) + 4\(\hat{j}\)
\(\vec{r}_{1}\) = \(\hat{i}\) + 2\(\hat{j}\)
Solution:
Displacement vector:
∆r= \(\vec{r}_{2}\) – \(\vec{r}_{1}\) = (1 – 3)\(\hat{i}\) + (2 – 4) \(\hat{j}\)
∆r = -2\(\hat{i}\) -2\(\hat{j}\) = -2(\(\hat{i}\) + \(\hat{j}\))

The Average Velocity calculator computes the velocity (V) based on the change in position (Δx) and the change in time (Δt).

Question 3.
Calculate the average velocity of the particle whose position vector changes from \(\vec{r}_{1}\) = 5\(\hat{i}\) + 6\(\hat{j}\) to \(\vec{r}_{2}\) = 2\(\hat{i}\) + 3 \(\hat{j}\) in a time 5 seconds.
Answer:
Given,
Position vectors of a particle
\(\vec{r}_{1}\) = 5\(\hat{i}\) + 6\(\hat{j}\),
\(\vec{r}_{2}\) = 2\(\hat{i}\) + 35\(\hat{j}\)
time(t) = 5s
Solution:

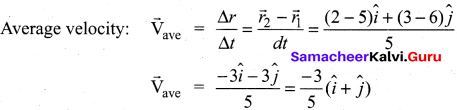
Question 4.
Convert the vector \(\overrightarrow{\mathrm{r}}\) = 3\(\hat{i}\) + 2\(\hat{j}\) into a unit vector.
Answer:
Given:
Position vector\(\hat{r}\) = 3\(\hat{i}\) + 2\(\hat{j}\)
Solution:

Question 5.
What are the resultants of the vector product of two given vectors given by \(\overrightarrow{\mathrm{A}}\) = 4\(\hat{i}\) – 2\(\hat{j}\) + \(\hat{k}\) and \(\overrightarrow{\mathrm{B}}\) = 5\(\hat{i}\) + 3\(\hat{j}\) – 4\(\hat{k}\) ?
Answer:
Given,
Vectors \(\overrightarrow{\mathrm{A}}\) = 4\(\hat{i}\) – 2\(\hat{j}\) + \(\hat{k}\)
\(\overrightarrow{\mathrm{B}}\) = 5\(\hat{i}\) + 3\(\hat{j}\) – 4\(\hat{k}\)
Solution:

Question 6.
object at an angle such that the horizontal range is 4 times of the maximum height. What is the angle of projection of the object?
Answer:
Give,
Horizontal range = 4H_max
Solution:

Question 7.
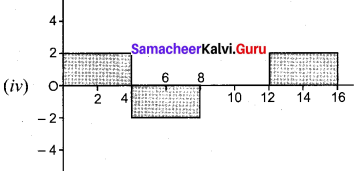
The following graphs represent velocity – time graph. Identity what kind of motion a particle undergoes in each graph.

Answer:
(a) At all the points, slope of the graph is constant.
∴ \(\overrightarrow{\mathrm{a}}\) = constant

(b) No change in magnitude of velocity with respect to time
∴ \(\overrightarrow{\mathrm{v}}\) = constant

(c) Slope of this graph is greater than graph (a) but constant
∴ \(\overrightarrow{\mathrm{a}}\) = constant but greater than the graph (a)

(d) At each point slope of the curve increases.
∴ \(\overrightarrow{\mathrm{a}}\) is a variable and object is in accelerated motion.

Question 8.
The following velocity – time graph represents a particle moving in the positive x-direction. Analyse its motion from 0 to 7 s. Calculate the displacement covered and distance travelled by the particle from 0 to 2 s.

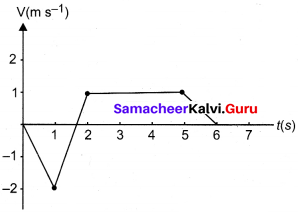
Answer:
As per graph,
(a) From 0 to 1.5 s the particle moving in a opposite direction.

• From 1.5 s to 2 s the particle is moving with increasing velocity.
• From 2 s to 5 s velocity of the particle is constant of magnitude 1 ms ^-1
• From 5 s to 6 s velocity of the particle is decreasing.
• From 6 s to 7 s the particle is at rest.

(b) Distance covered by the particle – Area covered under (v -t) graph

Displacement of the particle

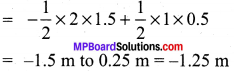
Question 9.
A particle is projected at an angle of θ with respect to the horizontal direction. Match the following for the above motion.
(a) v_x – decreases and increases
(b) v_y  – remains constant
(c) Acceleration – varies
(d) Position vector – remains downward
Answer:
(a) v_x = remains constant
(b) v_y = decreases and increases
(c) a = remains downward
(d) r = varies

Question 10.
A water fountain on the ground sprinkles water all around it. If the speed of the water coming out of the fountain is v, calculate the total area around the fountain that gets wet.
Answer:
Given,
Speed of water = v
Solution:
Water comes from a fountain can be taken as projectile and the distance covered is maximum range of projectile i.e. θ = 45°.
Range of the particle (R_max) = \(\frac{v^{2}}{g}\) sin 2θ = \(\frac{v^{2}}{g}\)
here, R_max is radius of the area covered.

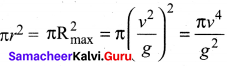
Question 11.
The following table gives the range of a particle when thrown on different planets. All the particles are thrown at the same angle with the horizontal and with the same initial speed. Arrange the planets in ascending order according to their acceleration due to gravity, (g value).

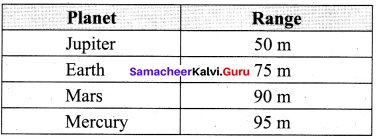
Answer:
Range = \(\frac{v^{2}}{g}\) sin 2θ ∴ g α \(\frac { 1 }{ range }\)
Ascending order of the planet with respect to their “g” is Mercury, Mars, Earth, Jupiter.

Question 12.
The resultant of two vectors A and B is perpendicular to vector A and its magnitude is equal to half of the magnitude of vector B. Then the angle between A and B is
(a) 30°
(b) 45°
(c) 150°
(d) 120°
Answer:
Given:
Resultant of \(\overrightarrow{\mathrm{A}}\) & \(\overrightarrow{\mathrm{B}}\) is perpendicular to \(\overrightarrow{\mathrm{A}}\) and magnitude of resultant (C) = \(\frac { 1 }{ 2 }\) \(\overrightarrow{\mathrm{B}}\) and α = 90°
Solution:
(i) Magnitude of resultant:

(ii) direction of resultant:

Question 13.
Compare the components for the following vector equations
(a) T\(\hat{j}\) -mg\(\hat{j}\) = ma\(\hat{j}\)
(b) \(\overrightarrow{\mathrm{T}}\) + \(\overrightarrow{\mathrm{F}}\) = \(\overrightarrow{\mathrm{A}}\) + \(\overrightarrow{\mathrm{B}}\)
(c) \(\overrightarrow{\mathrm{T}}\) – \(\overrightarrow{\mathrm{F}}\) = \(\overrightarrow{\mathrm{A}}\) – \(\overrightarrow{\mathrm{B}}\)
(d) T\(\hat{j}\) + mg\(\hat{j}\)= ma\(\hat{j}\)
Answer:
Components of the vectors
(a) T – mg = ma
(b) \(\overline{\mathrm{T}}_{x}+\overline{\mathrm{F}}_{x}\) = \(\overline{\mathrm{A}}_{x}+\overline{\mathrm{B}}_{x}\) (or) \(\overline{\mathrm{T}}_{y}+\overline{\mathrm{F}}_{y}=\overline{\mathrm{A}}_{y}+\overline{\mathrm{B}}_{y}\)
(c) \(\overline{\mathrm{T}}_{x}-\overline{\mathrm{F}}_{x}=\overline{\mathrm{A}}_{x}+\overline{\mathrm{B}}_{x}\)  (or) \(\overline{\mathrm{T}}_{y}-\overline{\mathrm{F}}_{y}=\overline{\mathrm{A}}_{y}+\overline{\mathrm{B}}_{y}\)
(d) T + mg = ma

Question 14.
Calculate the area of the triangle for which two of its sides are given by the vectors A = 5\(\hat{i}\) – 3\(\hat{j}\), B = 4\(\hat{i}\) + 6\(\hat{j}\) .
Answer:
Solution:
Area of the triangle = \(\frac { 1 }{ 2 }\) |\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{A}}\)|

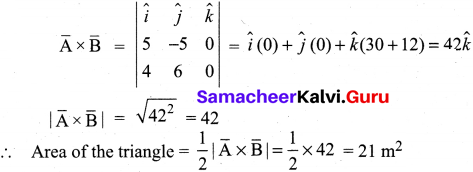
Question 15.
If Earth completes one revolution in 24 hours, what is the angular displacement made by Earth in one hour? Express your answer in both radian and degree.
Answer:
Given,
time period of earth = 24 hours
Solution:
Earth covers 360° in 24 hours
∴Angular displacement m 1 hour = \(\frac { 360° }{ 24 }\) = 15° (or) \(\frac { π }{ 12 }\)
Angular displacement in radian = \(\frac { 15° }{ 57.295° }\) = 0.262 rad

Question 16.
An object is thrown with initial speed 5 ms ^-1 with an angle of projection 30°. What is the height and range reached by the particle?
Answer:
Given,
Initial speed (u) = 5 ms^-1
Angle of projection θ = 30°
Solution:

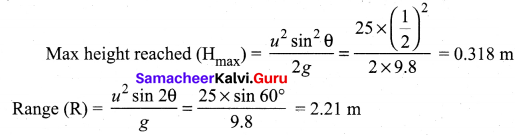
Question 17.
A foot – ball player hits the ball with speed 20 ms^-1 with angle 30° with respect to horizontal direction as shown in the figure. The goal post is at a distance of 40 m from him. Find out whether ball reaches the goal post.

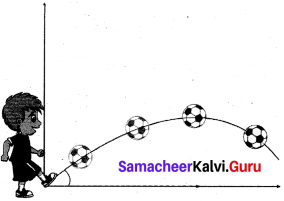
Answer:
Given:
Initial speed (u) = 20 ms^-1
Angle of projection (θ) = 30°
The distance of the goal post = 40 m
Solution:
Range of the projectile

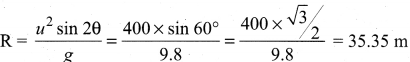
The distance of goal post is 40 m. But the range of the ball is 35.35 m only. So ball will not reach the goal post.

Question 18.
If an object is thrown horizontally with an initial speed 10 ms ^-1 from the top of a building of height 100 m. What is the horizontal distance covered by the particle?
Answer:
Given,
Initial speed =10 ms^-1
Height of the building (h) = 100 m
Range = ?
Solution:
Range of the object = R = \(u \sqrt{\frac{2 h}{g}}\) = 10\(\sqrt{\frac{200}{9.8}}\) = 45.1 m
R = 45 m.

Question 19.
An object is executing uniform circular motion with an angular speed of \(\frac { π }{ 12 }\) radian per second. At t = 0 the object starts at angle θ = 0. What is the angular displacement of the particle after 4 s?
Answer:
Given:
Angular speed = \(\frac { π }{ 12 }\) rad/ sec
Solution:
Angular speed = \(\frac { Angular displacement}{ time taken }\)
Angular displacement = \(\frac { π }{ 12 }\) x 4 = \(\frac { π }{ 12 }\) = 60°

Question 20.
Consider the x-axis as representing east, the v – axis as north and z – axis as vertically upwards. Give the vector representing each of the following points.
(a) 5 m north east and 2 m up
(b) 4 m south east and 3 m up
(c) 2 m north west and 4 m up
Answer:
Given,
Solution:
(a) Length along X – axis = 5 cos 45° = \(\frac{5}{\sqrt{2}}\)m
Length along Y- axis = 5 sin 45° = \(\frac{5}{\sqrt{2}}\)m
Length along Z – Axis = 2 m
In vector rotation = \(\frac{5}{\sqrt{2}}\)\(\hat{i}\) + \(\frac{5}{\sqrt{2}}\)\(\hat{j}\) + 2\(\hat{k}\) = \(\frac{5(\hat{i}+\hat{j})}{\sqrt{2}}\) + 2\(\hat{k}\)

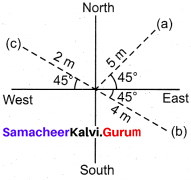
(b) Length along X = 4 cos 45° = \(\frac{4}{\sqrt{2}}\)m
Length along Y = 4 sin 45° = \(\frac{4}{\sqrt{2}}\)m
Length along Z-axis = 3 m
In vector rotation = \(\frac{4}{\sqrt{2}}\)\(\hat{i}\) – \(\frac{4}{\sqrt{2}}\)\(\hat{i}\) + 3k = 4(\(\hat{i}\) – \(\hat{j}\)) \(\sqrt{2}+3 \hat{k}\)

(c) Length along X = – 2 cos 45° = \(\sqrt{2}+3 \hat{k}\) = \(\frac{2}{\sqrt{2}} m=\sqrt{2} m\)
Length along Y = 2 sin 45° = \(\frac{2}{\sqrt{2}} m=\sqrt{2} m\)
length along Z = 4 m
∴ In vector rotation = \(-\sqrt{2} \hat{i}+\sqrt{2} \hat{j}+4 \hat{k}\)

Question 21.
The Moon is orbiting the Earth approximately once in 27 days, what is the angle transformed by the Moon per day?
Answer:
Given,
period of moon = 27 days
Solution:
i.e. in 27 days moon covers 360°
In one day angle traversed by moon = \(\frac { 360° }{ 2H }\) = 13.3°

Question 22.
An object of mass m has angular acceleration a = 0.2 rad s2. What is the angular displacement covered by the object after 3 second? (Assume that the object started with angle zero with zero angular velocity).
Answer:
Given,
Angular acceleration = α = 0.2 rad s^-2
Time = 3s
Initial velocity = 0
Solution:

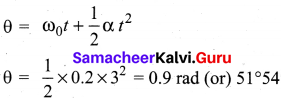
Samacheer Kalvi 11th Physics Kinematics Additional Questions Solved

Samacheer Kalvi 11th Physics Kinematics Multiple Choice Questions 

Question 1.
The radius of the earth was measured by –
(a) Newton
(b) Eratosthenes
(c) Galileo
(d) Ptolemy
Answer:
(b) Eratosthenes

Question 2
The branch of mechanics which deals with the motion of objects without taking force into account is –
(a) kinetics
(b) dynamics
(c) kinematics
(d) statics
Answer:
(c) kinematics

Question 3.
If the coordinate axes (x, y, z) are drawn in anticlockwise direction then the co-ordinate system is known as –
(a) Cartesian coordinate system
(b) right handed coordinate system
(c) left handed coordinate system
(d) cylindrical coordinate system
Answer:
(b) right handed coordinate system

Question 4.
The dimension of point mass is –
(a) 0
(b) 1
(c) 2
(d) kg
Answer:
(a) 0

Question 5.
If an object is moving in a straight line then the motion is known as –
(a) linear motion
(b) circular motion
(c) curvilinear motion
(d) rotational motion
Answer:
(a) linear motion

Question 6.
An athlete running on a straight track is an example for the whirling motion of a stone attached to’a string is a –
(a) linear motion
(b) circular motion
(c) curvilinear motion
(d) rotational motion
Answer:
(a) linear motion

Question 7.
The whirling motion of a stone attached to a string is a –
(a) linear motion
(b) circular motion
(c) curvilinear motion
(d) rotational motion
Answer:
(b) circular motion

Question 8.
Spinning of the earth about its own axis is known as –
(a) linear motion
(b) circular motion
(c) curvilinear motion
(d) rotational motion
Answer:
(d) rotational motion

Question 9.
If an object executes a to and fro motion about a fixed point, is an example for –
(a) rotational motion
(b) vibratory motion
(c) circular motion
(d) curvilinear motion
Answer:
(b) vibratory motion

Question 10.
Vibratory motion is also known as –
(a) circular motion
(b) rotational motion
(c) oscillatory motion
(d) spinning
Answer:
(c) oscillatory motion

Question 11.
The motion of satellite around the earth is an example for –
(a) circular motion
(b) rotational motion
(c) elliptical motion
(d) spinning
Answer:
(a) circular motion

Question 12.
An object falling freely under gravity close to earth is –
(a) one dimensional
(b) circular motion
(c) rotational motion
(d) spinning motion
Answer:
(a) one dimensional

Question 13.
Motion of a coin on a carrom board is an example of –
(a) one dimensional motion
(b) two dimensional motion
(c) three dimensional motion
(d) none
Answer:
(b) two dimensional motion

Question 15.
A bird flying in the sky is an example of –
(a) one dimensional motion
(b) two dimensional motion
(c) three dimensional motion
(d) none
Answer:
(c) three dimensional motion

Question 16.
Example for scalar is –
(a) distance
(b) displacement
(c) velocity
(d) angular momentum
Answer:
(a) distance

Question 17.
Which of the following is not a scalar?
(a) Volume
(b) angular momentum
(c) Relative density
(d) time
Answer:
(b) angular momentum

Question 18.
Vector is having –
(a) only magnitude
(b) only direction
(c) bot magnitude and direction
(d) either magnitude or direction
Answer:
(c) both magnitude and direction

Question 19.
“norm” of the vector represents –
(a) only magnitude
(b) only direction
(c) both magnitude and direction
(d) either magnitude or direction
Answer:
(a) only magnitude

Question 20.
If two vectors are having equal magnitude and same direction is known as –
(a) equal vectors
(b) col-linear vectors
(c) parallel vectors
(d) on it vector
Answer:
(a) equal vectors

Question 21.
The angle between two collinear vectors is / are –
(a) 0°
(b) 90°
(c) 180°
(d) 0° (or) 180°
Answer:
(d) 0° (or) 180°

Question 22.
The angle between parallel vectors is –
(a) 0°
(b) 90°
(c) 180°
(d) 0° (or) 180°
Answer:
(a) 0°

Question 23.
The angle between anti parallel vectors is –
(a) 0°
(b) 90°
(c) 180°
(d) 0° (or) 180°
Answer:
(c) 180°

Question 24.
Unit vector is –
(a) having magnitude one but no direction
(b) \(A \widehat{A}\)
(c) \(\frac{\widehat{A}}{A}\)
(d) |A|
Answer:
(c) \(\frac{\widehat{A}}{A}\)

Question 25.
A unit vector is used to specify –
(a) only magnitude
(b) only direction
(c) either magnitude (or) direction
(d) absolute value
Answer:
(b) only direction

Question 26.
The angle between any two orthogonal unit vectors is –
(a) 0°
(b) 90°
(c) 180°
(d) 360°
Answer:
(b) 90°

Question 27.
If \(\hat{n}\) is a unit vector along the direction of \(\overrightarrow{\mathrm{A}}\), the \(\hat{n}\) is-
(a) \(\overrightarrow{\mathrm{A}}\) A
(b) n x A
(c) \(\overrightarrow{\mathrm{A}} / \mathrm{A}\)
(d \(\overrightarrow{\mathrm{A}}\) |A|
Answer:
(c) \(\overrightarrow{\mathrm{A}} / \mathrm{A}\)

Question 28.
The magnitude of a vector can not be-
(a) positive
(b) negative
(e) zero
(cl) 90
Answer:
(b) negative

Question 29.
If R = P + Q, then which of the following is true?
(a) P > Q
(b) Q >P
(c) P = Q
(d) R > P, Q
Answer:
(d) R > P, Q

Question 30.
A force of 3 N and 4 N are acting perpendicular to an object, the resultant force is-
(a) 9 N
(b) 16 N
(c) 5 N
(d) 7 N
Answer:
(c) 5 N

Question 31.
Torque is a-
(a) scalar
(b) vector
(c) either scalar (or) vector
(d) none
Answer:
(6) vector

Question 32.
The resultant of \(\overrightarrow{\mathrm{A}}\) + \(\overrightarrow{\mathrm{B}}\) acts along x – axis. If A = 2\(\hat{i}\) – 3 \(\hat{j}\) + 2\(\hat{k}\) then B is-
(a) -2\(\hat{i}\) + \(\hat{j}\) + \(\hat{k}\)
(b) 3\(\hat{j}\) – 2\(\hat{k}\)
(c) -2\(\hat{i}\) -3 \(\hat{j}\)
(d) -2\(\hat{i}\) – 2\(\hat{k}\)
Answer:
(b) 3\(\hat{j}\) – 2\(\hat{k}\)

Question 33.
The angle between (\(\overrightarrow{\mathrm{A}}\) + \(\overrightarrow{\mathrm{B}}\)) and (\(\overrightarrow{\mathrm{A}}\) – \(\overrightarrow{\mathrm{B}}\)) can be –
(a) only 0°
(b) only 90°
(c) between 0° and 90°
(d) between 0° and 180°
Answer:
(d) between 0° and 180°

Question 34.
If a vector \(\overrightarrow{\mathrm{A}}\) = 3\(\hat{i}\) + 2\(\hat{j}\) then what is 4 A-
(a) 12\(\hat{i}\) + 8\(\hat{j}\)
(b) 0.75\(\hat{i}\) + 0.5\(\hat{j}\)
(c) 3\(\hat{i}\) + 2\(\hat{j}\)
(d) 7\(\hat{i}\) + 6\(\hat{j}\)
Answer:
(a) 12\(\hat{i}\) + 8\(\hat{j}\)

Question 35.
If P = mV then the direction of P along-
(a) m
(b) v
(c) both (a) and (b)
(d) neither m nor v
Answer:
(b) v

Question 36.
The scalar product \(\overrightarrow{\mathrm{A}}\). \(\overrightarrow{\mathrm{B}}\) is equal to-
(a) \(\overrightarrow{\mathrm{A}}\) + \(\overrightarrow{\mathrm{B}}\)
(b) AB sin θ
(c) AB cos θ
(d) \(\overrightarrow{\mathrm{A}}\) + \(\overrightarrow{\mathrm{B}}\)
Answer:
(c) AB cos θ

Question 37.
The scalar product \(\overrightarrow{\mathrm{A}}\).\(\overrightarrow{\mathrm{B}}\)is equal to-
(a) \(\overrightarrow{\mathrm{A}}\) +\(\overrightarrow{\mathrm{B}}\)
(b) \(\overrightarrow{\mathrm{A}}\). \(\overrightarrow{\mathrm{B}}\)
(c) AB sin θ
(d) (\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\)
Answer:
(b) \(\overrightarrow{\mathrm{A}}\). \(\overrightarrow{\mathrm{B}}\)

Question 38.
The scalar product of two vectors will be maximum when θ is equal to –
(a) 0°
(b) 90°
(c) 180°
(d) 270°
Answer:
(a) 0°

Question 39.
The scalar product of two vectors will be minimum. When θ is equal to –
(a) 0°
(b) 45°
(c) 180°
(d) 60°
Answer:
(c) 180°

Question 40.
The vectors A and B to be mutually orthogonal when –
(a) \(\overrightarrow{\mathrm{A}}\) + \(\overrightarrow{\mathrm{B}}\) = 0
(b) \(\overrightarrow{\mathrm{A}}\) –\(\overrightarrow{\mathrm{B}}\) = 0
(c) \(\overrightarrow{\mathrm{A}}\).\(\overrightarrow{\mathrm{B}}\) = 0
(d) \(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\) = 0
Answer:
(c) \(\overrightarrow{\mathrm{A}}\).\(\overrightarrow{\mathrm{B}}\) = 0

Question 41.
The magnitude of the vector is –
(a) A²
(b) \(\sqrt{\mathrm{A}^{2}}\)
(c) \(\sqrt{\mathrm{A}}\)
(d) \(\sqrt[3]{\mathrm{A}}\)
Answer:
(b) \(\sqrt{\mathrm{A}^{2}}\)

Question 42.
\(\hat{i}\) .\(\hat{j}\) is –
(a) 0
(b) I
(c) ∞
(d) none
Answer:
(a) 0

Question 43.
If \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) are two vectors, which are acting along x, y respectively, then \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) lies along –
(a) x
(b) y
(c) z
(d) none
Answer:
(c) z

Question 44.
The direction of \(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\) is given by-
(a) right hand screw rule
(b) right hand thumb rule
(c) both (a) and (b)
(d) neither (a) and (b)
Answer:
(c) both (a) and (b)

Question 45.
\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\) is –
(a) AB cos θ
(b) AB sin θ
(c) AB tan θ
(d) AB sec θ
Answer:
(b) AB sin θ

Question 46.
\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\) isequal to –
(a) \(\overrightarrow{\mathrm{B}}\) x \(\overrightarrow{\mathrm{A}}\)
(b) \(\overrightarrow{\mathrm{A}}\) + \(\overrightarrow{\mathrm{B}}\)
(c) –\(\overrightarrow{\mathrm{B}}\) x \(\overrightarrow{\mathrm{A}}\)
(d) \(\overrightarrow{\mathrm{A}}\) – \(\overrightarrow{\mathrm{B}}\)
Answer:
(c) –\(\overrightarrow{\mathrm{B}}\) x \(\overrightarrow{\mathrm{A}}\)

Question 47.
The vector product of any two vectors gives a –
(a) vector
(b) scalar
(e) tensor
(d) col-linear
Answer:
(a) vector

Question 48.
|\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\)| is equal to –
(a) -|\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\)|
(b) |\(\overrightarrow{\mathrm{B}}\) x \(\overrightarrow{\mathrm{A}}\)|
(c) -|\(\overrightarrow{\mathrm{B}}\) x \(\overrightarrow{\mathrm{A}}\)|
(d) \( \frac{\overline{\mathrm{A}} \times \overline{\mathrm{B}}}{|\overline{\mathrm{A}} \times \overline{\mathrm{B}}|}\)
Answer:
(b) |\(\overrightarrow{\mathrm{B}}\) x \(\overrightarrow{\mathrm{A}}\)|

Question 49.
The vector product of two vectors will have maximum magnitude when θ is equal to –
(a) 0°
(b) 90°
(c) 180°
(d) 360°
Answer:
(b) 90°

Question 50.
The vector product of two non-zero vectors will be minimum when O is equal to –
(a) 0°
(b) 180°
(e) both (a) and (b)
(d) neither (a) nor (b)
Answer:
(e) both (a) and (b)

Question 51.
The product of a vector with itself is equal to –
(a) 0
(b) 1
(c) ∞
(d) A²
Answer:
(a) 0

Question 52.
\(\hat{i}\) x \(\hat{i}\) is –
(a) 0
(b) 1
(c) ∞
(d) \(\hat{j}\)
Answer:
(a) 0

Question 53.
\(\hat{i}\) x \(\hat{j}\) is –
(a) \(\hat{i}\)
(b) \(\hat{j}\)
(c) \(\hat{k}\)
(d) \(\overrightarrow{\mathrm{z}}\)
Answer:
(c) \(\hat{k}\)

Question 54.
\(\hat{j}\) x \(\hat{i}\) is –
(a) –\(\hat{i}\)
(b) –\(\hat{j}\)
(c) –\(\hat{k}\)
(d) \(\overrightarrow{\mathrm{z}}\)
Answer:
(c) –\(\hat{k}\)

Question 55.
If two vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) form adjacent sides of parallelogram, then the magnitude of |\(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\)| will give of parallelogram –
(a) length
(b) area
(c) volume
(d) diagonal
Answer:
(b) area

Question 56.
If \(\overrightarrow{\mathrm{P}}\) – \(\overrightarrow{\mathrm{Q}}\) then which of the following is incorrect. –
(a) \(\hat{P}\) = \(\hat{Q}\)
(b) |\(\hat{P}\)| = |\(\hat{Q}\)|
(c) P\(\hat{Q}\) = Q\(\hat{A}\)
(d) \(\hat{P}\) \(\hat{Q}\) = PQ
Answer:
(d) \(\hat{P}\) \(\hat{Q}\) = PQ

Question 57.
The momentum of a particle is \(\overrightarrow{\mathrm{P}}\) = cos θ \(\hat{i}\) + sin θ \(\hat{j}\) . The angle between momentum and the force acting on a body is –
(a) 0°
(b) 45°
(c) 90°
(d) 180°
Answer:
(c) 90°

Question 58.
A and B are two vectors, if A and B are perpendicular to each other then –
(a) \(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\) = 0
(b) \(\overrightarrow{\mathrm{A}}\) x \(\overrightarrow{\mathrm{B}}\) = l
(c) \(\overrightarrow{\mathrm{A}}\) \(\overrightarrow{\mathrm{B}}\) = 0
(d) \(\overrightarrow{\mathrm{A}}\) \(\overrightarrow{\mathrm{B}}\) = \(\overrightarrow{\mathrm{A}}\)\(\overrightarrow{\mathrm{B}}\)
Answer:
(c) \(\overrightarrow{\mathrm{A}}\) \(\overrightarrow{\mathrm{B}}\) = 0

Question 59.
The angle between two vectors -3\(\hat{i}\) + 6\(\hat{k}\) and 2\(\hat{i}\) + 3\(\hat{j}\) + \(\hat{k}\) is –
(a) 0°
(b) 45°
(c) 60°
(d) 90°
Answer:
(d) 90°

Question 60.
The radius vector is 2\(\hat{i}\) + \(\hat{j}\) + \(\hat{k}\) while linear momentum is 2\(\hat{i}\) + 3\(\hat{j}\) + \(\hat{k}\) Then the angular momentum is
(a) -2\(\hat{i}\) + 4\(\hat{k}\)
(b) 4\(\hat{i}\) – 8\(\hat{k}\)
(c) 2\(\hat{k}\) – 4\(\hat{j}\) + 2\(\hat{k}\)
(d) 4\(\hat{i}\) – 8\(\hat{j}\)
Answer:
(a) -2\(\hat{i}\) + 4\(\hat{k}\)

Question 61.
Which of the following cannot be a resultant of two vectors of magnitude 3 and 6?
(a) 3
(b) 6
(c) 10
(d) 7
Answer:
(c) 10

Question 62.
Twelve forces each of magnitude 10 N acting on a body at an angle of 30° with other forces then their resultant is-
(a) 10 N
(b)120 N
(c) \(\frac{10}{\sqrt{3}}\)
(d) zero

Question 63.
Two forces are in the ratio of 3 : 4. The maximum and minimum of their resultants are in the ratio is –
(a) 4 : 3
(b) 3 : 4
(c) 7 : 1
(d) 1 : 7
Answer:
(c) 7 : 1

Question 64.
If | \(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\) | = |\(\overrightarrow{\mathrm{P}}\) | + |\(\overrightarrow{\mathrm{Q}}\)|. The angle between the vectors \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) is –
(a) 0°
(b) 180°
(c) 60°
(d) 90°
Answer:
(a) 0°
|\(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\) | = |\(\overrightarrow{\mathrm{P}}\) | + |\(\overrightarrow{\mathrm{Q}}\)|
Square on both sides and the resultant becomes
P² + Q² + 2PQ cos θ = P² + Q² + 2PQ cos θ = 1
θ = 0

Question 65.
If |\(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\) = |\(\overrightarrow{\mathrm{P}}\) | — |\(\overrightarrow{\mathrm{P}}\)|, then the angle between the vectors \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\)
(a) 0°
(b) 90°
(c) 180°
(d) 360°
Answer:
(c) |\(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\)| = |\(\overrightarrow{\mathrm{P}}\) | |\(\overrightarrow{\mathrm{P}}\)| ‘
Square on both side, and the resultant becomes
P² + Q² + 2PQ cos θ = P² + Q² – 2PQ .
cos θ = -1
θ = 180°

Question 66.
If |\(\overrightarrow{\mathrm{P}}\) x \(\overrightarrow{\mathrm{Q}}\)| = |\(\overrightarrow{\mathrm{P}}\) . \(\overrightarrow{\mathrm{Q}}\)| then angle between \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) then angle between P and Q will be –
(a) 0°
(b) 30°
(c) 45°
(d) 60°
Answer:
(c) |\(\overrightarrow{\mathrm{P}}\) x \(\overrightarrow{\mathrm{Q}}\)| = |\(\overrightarrow{\mathrm{P}}\) . \(\overrightarrow{\mathrm{Q}}\)| Expand the terms
PQ sinθ = PQ cos θ
tan θ = 1
θ = 45°

Question 67.
If | \(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\) | = |\(\overrightarrow{\mathrm{P}}\) | |\(\overrightarrow{\mathrm{Q}}\)|, then angle between \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) will be –
(a) 0°
(b) 45°
(c) 90°
(d) 180°
Answer:
(c) | \(\overrightarrow{\mathrm{P}}\) + \(\overrightarrow{\mathrm{Q}}\) | = |\(\overrightarrow{\mathrm{P}}\)| |\(\overrightarrow{\mathrm{Q}}\) |
Square on both side, and the resultants become,
P² + Q² + 2PQ cos 0 = P² + Q² – 2PQ cos θ 4PQ cos θ = 0
θ = 90°

Question 68.
If A and B are the sides of triangle, then area of triangle –
(a) \(\frac{1}{2}|\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}|\)
(b) \(\frac{1}{2}|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|\)
(c) AB sin θ
(d) AB cos θ
Answer:
(b) \(\frac{1}{2}|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|\)

Question 69.
A particle moves in a circular path of radius 2 cm. If a particle completes 3 rounds, then the distance and displacement of the particle are –
(a) 0 and 37.7
(b) 37.7 and 0
(c) 0 and 0
(d) 37.7 and 37.7
Answer:
(b) Radius = 2 cm
Circumference of the circle = 2nr = 4n cm
Distance covered in 3 rounds = 127r cm = 37.7 cm
Initial and final positions are same
∴ Displacement = 0

Question 70.
If rx and r2 are position vectors, then the displacement vector is –
(a) \(\vec{r}_{1} \times \vec{r}_{2}\)
(b) \(\vec{r}_{1} \cdot \vec{r}_{2} \)
(c) \(\vec{r}_{1}+\vec{r}_{2}\)
(d) \(\vec{r}_{2}+\vec{r}_{1} \)
Answer:
(d) \(\vec{r}_{2}+\vec{r}_{1} \)

Question 71.
The ratio of the displacement vector to the corresponding time interval is –
(a) average speed
(b) average velocity
(c) instantaneous speed
(d) instantaneous velocity
Answer:
(b) average velocity

Question 72.
The ratio of total path length travelled by the particle in a time interval –
(a) average speed
(b) average velocity
(c) instantaneous speed
(d) instantaneous velocity
Answer:
(a) average speed

Question 73.
The product of mass and velocity of a particle is –
(a) acceleration
(b) force
(c) torque
(d) momentum
Answer:
(d) momentum

Question 74.
The area under the force, displacement curve is –
(a) potential energy
(b) work done.
(c) impulse
(d) acceleration
Answer:
(b) work done

Question 75.
The area under the force, time graph is –
(a) momentum
(b) force
(c) work done
(d) impulse
Answer:
(d) impulse

Question 76.
The unit of momentum is –
(a) kg ms^-1
(b) kg ms^-2
(c) kg m²s^-1
(d) kg^-1 m² s^-1
Answer:
(b) kg ms^-2

Question 77.
The slope of the position – time graph will give –
(a) displacement
(b) velocity
(c) acceleration
(d) force
Answer:
(d) force

Question 78.
The area under velocity-time graph gives-
(a) positive
(b) negative
(c) either positive (or) negative
(d) zero
Answer:
(c) either positive (or) negative

Question 79.
The magnitude of distance is always-
(a) positive
(b) negative
(c) either positive (or) negative
(d) zero
Answer:
(a) positive

Question 80.
If two objects A and B are moving along a straight line in the same direction with the velocities v_A and v_B respectively, then the relative velocity is-
(a) v_A + v_B
(b) v_A – v_B
(c) v_A v_B
(d) v_A / v_B
Answer:
(b) V_A – V_B

Question 81.
If two objects A and B are moving along a straight line in the opposite direction with the velocities V_A and V_B respectively, then relative velocity is-
(a) V_A + V_B
(b) V_A – V_B
(c) V_{A .} V_B
(d) V_A / V_B
Answer:
(a) V_A + V_B

Question 82.
If two objects moving with a velocities of V_A and V_B at an angle of 0 between them, the relative velocity is –

Answer:

Question 83.
A person moving horizontally with velocity \(\overrightarrow{\mathrm{V}_{m}}\) The relative velocity of rain with respect to the person is –
(a) \(\mathrm{V}_{\mathrm{R}}+\mathrm{V}_{\mathrm{m}}\)
(b) \(\sqrt{\mathrm{V}_{\mathrm{R}}+\mathrm{V}_{m}}\)
(c) \(\mathrm{V}_{\mathrm{R}}-\mathrm{V}_{m}\)
(d) \(\sqrt{\mathrm{v}_{\mathrm{R}}^{2}+\mathrm{V}_{m}^{2}}\)
Answer:
(d) \(\sqrt{\mathrm{v}_{\mathrm{R}}^{2}+\mathrm{V}_{m}^{2}}\)

Question 84.
A person moving horizontally with velocity \(\overrightarrow{\mathrm{V}_{m}}\) . Rain falls vertically with velocity \(\overrightarrow{\mathrm{V}_{R}}\) To save himself from the rain, he should hold an umbrella with vertical at an angle of –
(a) \(\tan ^{-1}\left(\frac{V_{R}}{V_{m}}\right)\)
(b) \(\tan ^{-1}\left(\frac{V_{m}}{V_{R}}\right)\)
(c) \(\tan \theta=\mathrm{V}_{m}+\mathrm{V}_{\mathrm{R}}\)
(d) \(\tan ^{-1}\left(\mathrm{V}_{\mathrm{R}}+\mathrm{V}_{m} / \mathrm{V}_{\mathrm{R}}-\mathrm{V}_{m}\right)\)
Answer:
(b) \(\tan ^{-1}\left(\frac{V_{m}}{V_{R}}\right)\)

Question 85.
A car starting from rest, accelerates at a constant rate x for sometime after which it decelerates at a constant rate v to come to rest. If the total time elapsed is t, the maximum velocity attained by the car is given by –

Answer:

Question 86.
A car covers half of its journey with a speed of 10 ms^-1 and the other half by 20 ms^-1. The average speed of car during the total journey is –
(a) 70 ms^-1
(b) 15 ms^-1
(c) 13.33 ms^-1
(d) 7.5 ms^-1
Answer:
(c) Let x is the total distance
Time to cover 1st half = \(\frac{x / 2}{10}\)
Time to cover 2nd half = \(\frac{x / 2}{20}\)
Average speed =

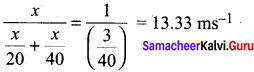
Question 87.
A swimmer can swim in still water at of 10 ms^-1 While crossing a river his average speed is 6 ms^-1. If he crosses the river in the shortest possible time, what is the speed of flow of water?
(a) 16 ms^-1
(b) 4 ms^-1
(c) 60 ms^-1
(d) 8 ms^-1
Answer:
(d) The resultant velocity of swimmer must be perpendicular to speed of water to cross the river in a shortest time
∴ \(v_{s}^{2}=v^{2}+v_{w}^{2}\)
\(v_{w}^{2}=v_{s}^{2}-v^{2}\) = 100 – 36 = 64
∴ V = 8 m/s^-1

Question 88.
A 100 m long train is traveling from North to South at a speed of 30 ms^-1. A bird is flying from South to North at a speed of 10^-1. How long will the bird take to, cross the train?
(a) 3 s
(b) 2.5 s
(c) 10 s
(d) 5 s
Answer:
(b) Length of train = 100 m
Relative velocity = 30 + 10 = 40 ms^-1
Time taken to cross the train (t) = \(\frac {distance}{ R.velocity }\) = \(\frac { 100 }{ 40 }\) = 2.5 s

Question 89.
The first derivative of position vector with respect to time is –
(a) velocity
(b) acceleration
(c) force
(d) displacement
Answer:
(a) velocity

Question 90.
The second derivative of position vector with respect to time is –
(a) velocity
(b) acceleration
(c) force
(d) displacement
Answer:
(b) acceleration

Question 91.
The slope of displacement-time graph gives –
(a) velocity
(b) acceleration
(c) force
(d) displacement
Answer:
(a) velocity

Question 92.
The slope of velocity-time graph gives –
(a) velocity
(b) acceleration
(c) force
(d) displacement
Answer:
(b) acceleration

Question 93.
The position vector of a particle is \(\vec{r}\) = 4t²\(\hat{i}\) + 2t\(\hat{j}\) + 3t\(\hat{k}\) The acceleration of a particle is having only –
(a) X – component
(b) Y – component
(c) Z – component
(d) X – Y component
Answer:
(a) X – component
4t²\(\hat{i}\) + 2t\(\hat{j}\) + 3t\(\hat{k}\)
\(\vec{v}\) = \(\frac{d \vec{r}}{dt}\) = 8t\(\hat{i}\) + 2\(\hat{j}\)
a = \(\frac{d^{2} r}{d t^{2}}\) = 8\(\hat{i}\) a is having only X-component.

Question 94.
The position vector of a particle is \(\vec{r}\) = 4t²\(\hat{i}\) + 2t\(\hat{j}\) + 3t\(\hat{k}\). The speed of the particle at t = 5 s is –
(a) 42 ms^-1
(b) 3s
(c) 3 ms^-1
(d) 40 ms^-1
Answer:
(a) 42 ms^-1
\(\vec{r}\) = 4t²\(\hat{i}\) + 2t\(\hat{j}\) + 3t\(\hat{k}\)
Speed v = — = \(\frac{d \vec{r}}{dt}\) = 8t\(\hat{i}\) + 2\(\hat{j}\)
at t = 5 s v = 40 + 2 = 42

Question 95.
An object is moving in a straight line with uniform acceleration a, the velocity-time relation is –
(a) u = v + at
(b) v = u + at
(c) v² = u² + a²t²
(d) v² – u² = at
Answer:
(b) v = u + at

Question 96.
An object is moving in a straight line with uniform acceleration, the displacement-time relation is –
(a) S = \(u t^{2}+\frac{1}{2} a t^{2}\)
(b) S = \(u t-\frac{1}{2} a t^{2}\)
(c) S = \(u t+\frac{1}{2} a t^{2}\)
(d) S = \(u t-a t^{2}\)
Answer:
(c) S = \(u t+\frac{1}{2} a t^{2}\)

Question 97.
An object is moving in a straight line with uniform acceleration, the velocity-displacement reflation is –
(a) V = u + 2as
(b) S = ut + -at
(c) V² = u² – 2as
(d) V² = u² + 2as
Answer:
(d) V² = u² + 2as

Question 98.
For free-falling body, its initial velocity is –
(a) 0
(b) 1
(c) ∞
(d) none
Answer:
(a) 0

Question 99.
An object falls from a height h (h<<R), the speed of the object when it reaches the ground is –
(a) \(\frac{1}{2} g t^{2}\)
(b) \(\sqrt{g t}\)
(c) gh
(d) \(\sqrt{2 g h}\)
Answer:
(d) \(\sqrt{2 g h}\)

Question 100.
An object falls from a height h (h<< R) the time taken by an object to reaches the ground is –
(a) \(\frac{1}{2} g t^{2}\)
(b) \(\sqrt{2 g h}\)
(c) \(\sqrt{\frac{2 h}{g}}\)
(d) \(\sqrt{\frac{2 g}{h}}\)
Answer:
(d) \(\sqrt{\frac{2 g}{h}}\)

Question 101.
In the absence of air resistance, horizontal velocity of the projectile is –
(a) always negative
(b) equal to ‘g’
(c) directly proportional to g
(d) a constant
Answer:
(d) a constant

Question 102.
In the horizontal projection, the range of the projectile is –
(a) \(\sqrt{\frac{2 h}{g}}\)
(b) \(u \sqrt{\frac{h}{g}}\)
(c) \(u \sqrt{\frac{2 h}{g}}\)
(d) \(u \sqrt{\frac{g}{2 h}}\)
Answer:
(c) \(u \sqrt{\frac{2 h}{g}}\)

Question 103.
In oblique projection, maximum height attained by the projectile is –
(a) \(\frac { t }{ u cos θ }\)
(b) \(\frac { u cos θ }{ 2g }\)
(c) \(\frac { 2g }{ u cos θ }\)
(d) \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)
Answer:
(d) \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)

Question 104.
In oblique projection time of flight of a projectile is –
(a) \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)
(b) \(\frac { 2u cos θ }{ g }\)
(c) \(\frac{u^{2} \sin 2 \theta}{g}\)
(d) \(\frac{u^{2}}{g}\)
Answer:
(b) \(\frac { 2u cos θ }{ g }\)

Question 105.
In oblique projection horizontal range of the projectile is –
(a) \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)
(b) \(\frac { 2u cos θ }{ g }\)
(c) \(\frac{u^{2} \sin 2 \theta}{g}\)
(d) \(\frac{u^{2}}{g}\)
Answer:
(a) \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)

Question 106.
In oblique projection, maximum horizontal range of the projectile is –
(a) \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)
(b) \(\frac { 2u cos θ }{ g }\)
(c) \(\frac{u^{2} \sin 2 \theta}{g}\)
(d) \(\frac{u^{2}}{g}\)
Answer:
(d) \(\frac{u^{2}}{g}\)

Question 107.
One radian is equal to –
(a) \(\frac {π}{ 180 }\) degree
(b) 60°
(c) 57.295°
(d) 53.925°
Answer:
(c) 57.295°

Question 108.
In relation between linear and angular velocity is –
(a) ω = vr
(b) ω = \(\frac {v }{ r }\)
(c) ω = \(\frac { r}{ v }\)
(d) ω = \(\frac { r }{ ω }\)
Answer:
(b) ω = \(\frac {v }{ r }\)

Question 109.
Centripetal acceleration is given by –
(a) \(\frac{v^{2}}{r}\)
(b) \(-\frac{v^{2}}{r}\)
(c) \(\frac{r}{v^{2}}\)
(d) \(-\frac{r}{v^{2}}\)
Answer:
(b) \(-\frac{v^{2}}{r}\)

Question 110.
In uniform circular motion –
(a) Speed changes but velocity constant
(b) Velocity changes but speed constant
(c) both speed and velocity are constant
(d) both speed and velocity are variable
Answer:
(b) Velocity changes but speed constant

Question 111.
In non – uniform circular motion, the resultant acceleration is given by –

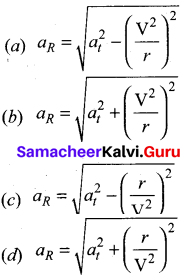
Answer:

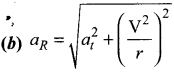
Question 112.
In non – uniform circular motion, the resultant acceleration makes an angle with the radius vector is –

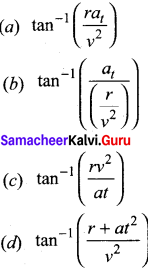
Answer:

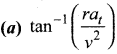
Question 113.
A compartment of an uniformly moving train is suddenly detached from the train and stops after covering some distance. The distance covered by the compartment and distance covered by the train in the given time –
(a) both will be equal
(b) second will be half of first
(c) first will be half of second
(d) none
Answer:
(c) first will be half of second

Question 114.
An object is dropped from rest. Its v – t graph is –

Answer:

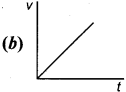
Question 115.
When a ball hits the ground as free fall and renounces but less than its original height? Which is represented by –

Answer:

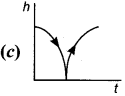
Question 116.
Which of the following graph represents the equation y = mx – C?

Answer:

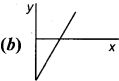
Question 117.
Which of the following graph represents the equation y = mx + C?

Answer:

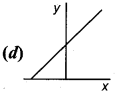
Question 118.
Which of the following graph represents the equation y = mx?

Answer:

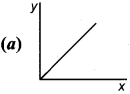
Question 119.
Which of the following graph represents the equation y = -mx + C?

Answer:

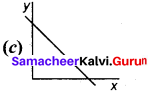
Question 120.
Which of the following graph represents the equation y = kx²?

Answer:

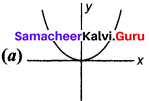
Question 121.
X = -ky² is represented by –

Answer:

Question 122.
X = ky² is represented by –

Answer:

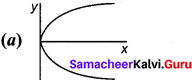
Question 123.
y = kx² is represented by –

Answer:

Question 124.
X °∝\(\frac { 1 }{ Y }\) (or) XY = constant is represented by –

Answer:

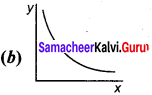
Question 125.
y = e^-kx is represented by –

Answer:

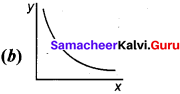
Question 126.
Y = 1 – e^-kx is represented by –

Answer:

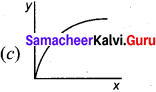
Question 127.
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 is represented by –

Answer:

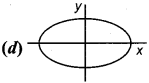
Question 128.
Let y =f(x) is a function. Its maxima (or) minima can be obtained by –
(a) y = 0
(b) f(x) = 0
(c) \(\frac {dy}{dx}\) = 0
(d) \(\frac{d^{2} y}{d x^{2}}\) = 0
Answer:
(c) \(\frac {dy}{dx}\) = 0

Question 129.
A particle at rest starts moving in a horizontal straight line with uniform acceleration. The ratio of the distance covered during the fourth and the third second is –
(a) \(\frac {4}{ 3 }\)
(b) \(\frac { 26 }{ 9 }\)
(e) \(\frac { 7}{ 5 }\)
(d) 2
Answer:
(c) The distance travelled during nth second –
S_n  = u + \(\frac { 1 }{ 2 }\) a (2n -1)
Distance travelled during 4th second S₁ = \(\frac { 1 }{ 2 }\) (8 – 1)
Distance travelled during 3rd second S₂ = \(\frac { 1 }{ 2 }\) a(6 – 1)
\(\frac{\mathrm{S}_{1}}{\mathrm{S}_{2}}\) = \(\frac { 7 }{ 5 }\)

Question 130.
The distance travelled by a body, falling freely from rest in t = 1s, t = 2s and t = 3s are in the ratio of –
(a) 1 : 2 : 3
(h) 1 : 3 : 5
(c) 1 : 4 : 9
(d) 9 : 4 : 1
Answer:
(c) The distance travelled by a free falling body S = \(\frac { 1 }{ 2 }\) gt²
∴ S α t²
∴ S₁ : S₂  : S₃ : 1² : 2² : 3² = 1 : 4 : 9.

Question 131.
The displacement of the particle along a straight line at time ¡ is given by X = a + ht + ct² where a, b, c are constants. The acceleration of the particle is-
(a) a
(b) b
(c) c
(d) 2c
Answer:
(d) X = a + bt + ct²
\(\frac { dX }{ dt }\) = v = b + 2ct
Acceleration = \(\frac{d^{2} X}{d t^{2}}\) = 2c.

Question 132.
Two bullets are fired at an angle of θ and (90 – θ) to the horizontal with same speed. The ratio of their times of flight is –
(a) 1 : 1
(b) 1: tan θ
(c) tan θ : 1
(d) tan² θ : 1
Answer:
(c) Time of flight t_f =  \(\frac { 2x sinθ}{ 9 }\)
t_f α sinθ
∴ \(\frac{t_{f_{1}}}{t_{f_{2}}}\) = \(\frac { sinθ }{sin (90 – θ) }\) = \(\frac { sinθ }{cos θ }\) = tanθ
\(t_{f_{1}}: t_{f_{2}}\) = tan θ : 1

Question 133.
A particle moves along a circular path under the action of a force. The work done by the force is –
(a) positive and non zero
(b) zero
(c) negative and non-zero
(d) none
Answer:
(b) zero

Question 134.
For a particle, revolving in a circle with speed, the acceleration of the particle is –
(a) along the tangent
(b) along the radius
(c) along its circumference
(d) zero
Answer:
(b) along the radius

Question 135.
A gun fires two bullets with same velocity at 60° and 30° with horizontal. The bullets strike at the same horizontal distance. The ratio of maximum height for the two bullets is in the ratio of –
(a) 1 : 2
(b) 3 : 1
(c) 2 : 1
(d) 1 : 3
Answer:
(b) 3 : 1
Max height attained h_max = \(\frac{u^{2} \sin ^{2} \theta}{2 g}\)
∴ h_max α sin² θ i.e h_max α \(\frac { 1-cos2θ}{ 2 }\)
\(\frac{h_{\max 1}}{h_{\max } 2}\) = \(\frac{3 / 2}{1 / 2}\) = 3

Question 136.
A ball is thrown vertically upward. it is a speed of lo m/s. When it has reached one half of its maximum height. I-low high does the ball rise? (g = 10 ms^-2)
(a) 5 m
(b) 7 m
(c) 10 m
(d) 12 m
Answer:
(c) 10 m

Question 137.
A car moves from X to Y with a uniform speed V_n  and returns to Y with a uniform speed V_d The average speed for this round trip is –

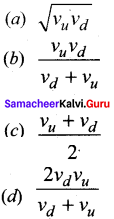
Answer:

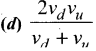
Question 138.
Two projectiles of same mass and with same velocity are thrown at an angle of 60° and 30° with the horizontal then which of the following will remain same?
(a) time of flight
(b) range of projectile
(c) maximum height reached
(d) all the above
Answer:
(b) range of projectile

Question 139.
A n object of mass 3 kg is at rest. Now a force of \(\overrightarrow{\mathrm{F}}\) = 6 t²\(\hat{i}\) + 4t\(\hat{j}\) is applied on the object, then the velocity of object at t = 3 second is –
(a) 18\(\hat{i}\) + 3 \(\hat{j}\)
(b) 18\(\hat{i}\) + 6\(\hat{j}\)
(c) 3 \(\hat{i}\) + 18\(\hat{j}\)
(d) 18 \(\hat{i}\) + 4\(\hat{j}\)
Answer:
(b) F = 6 t²\(\hat{i}\) + 4t\(\hat{j}\)

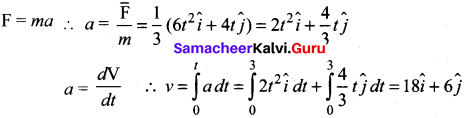
Question 140.
The angle for which maximum height and horizontal range are same for a projectile is –
(a) 32°
(b) 48°
(c) 76°
(d) 84°
Answer:
(c) 76°
H_max = horizontal range
\(\frac{u^{2} \sin ^{2} \theta}{2 g}\) = \(\frac{u^{2} \sin 2 \theta}{g}\)
\(\frac{\sin ^{2} \theta}{2}\) = 2 sin θ cos θ = sin θ = 4 cos θ tan θ = 4 θ = 76°

Question 141.
A bullet is dropped from some height, when another bullet is fired horizontally from the same height. They will hit the ground –

(a) depends upon mass of bullet
(b) depends upon the observer
(c) one after another
(d) simultaneously
Answer:
(d) simultaneously

Question 142.
From this velocity – time graph, which of the following is correct?
(a) Constant acceleration
(b) Variable acceleration
(c) Constant velocity
(d) Variable acceleration
Answer:
(b) Variable acceleration

Question 143.
When a projectile is at its maximum height, the direction of its velocity and acceleration are –
(a) parallel to each other
(b) perpendicular to each other
(c) anti – parallel to each other
(d) depends on its speed
Answer:
(b) perpendicular to each other

Question 144.
At the highest point of oblique projection, which of the following is correct?
(a) velocity of the projectile is zero
(b) acceleration of the projectile is zero
(c) acceleration of the projectile is vertically downwards
(d) velocity of the projectile is vertically downwards
Answer:
(c) acceleration of the projectile Is vertically downwards

Question 145.
The range of the projectile depends –
(a) The angle of projection
(b) Velocity of projection
(c) g
(d) all the above
Answer:
(d) all the above

Question 146.
A constant force is acting on a particle and also acting perpendicular to the velocity of the particle. The particle describes the motion in a plane. Then –
(a) angular displacement is zero
(b) its velocity is zero
(c) it velocity is constant
(d) it moves in a circular path
Answer:
(d) it moves in a circular path

Question 147.
If a body moving in a circular path with uniform speed, then –
(a) the acceleration is directed towards its center
(b) velocity and acceleration are perpendicular to each other
(c) speed of the body is constant but its velocity is varying
(d) all the above
Answer:
(d) all the above

Question 148.
A body is projected vertically upward with the velocity y = 3\(\hat{i}\) + 4\(\hat{j}\) ms-¹. The maximum height attained by the body is (g 10 ms^-2).
(a) 7 m
(b) 1.25 m
(c) 8 m
(d) 0.08 m
Answer:
(b) v = 3\(\hat{i}\) + 4\(\hat{j}\)
H_max = \(\frac{v^{2} \sin ^{2} \theta}{2 g}\) = \(\frac{v^{2}}{2 g}\) [ θ = 90 ]
v = \(\sqrt{9+16}\)  = \(\sqrt{25}\)
v² = 25
H_max = \(\frac{25}{20}\)  = \(\frac { 5 }{ 4 }\) = 1.25 m

Samacheer Kalvi 11th Physics Kinematics Short Answer Questions – I (1 Mark)

Question 1.
What is frame of reference?
Answer:
In a coordinate system, the position of an object is described relative to it, then such a coordinate system is called as frame of reference.

Question 2.
What are the types of motion?
Answer:

• Linear motion
• Circular motion
• Rotational motion
• Vibratory motion.

Question 3.
What is linear motion? Give example.
Answer:
An object is said to be in linear motion if it moves in a straight line.
Example – an athlete running on a straight track.

Question 4.
What is circular motion? Give example.
Answer:
Circular motion is defined as a motion described by an object traversing a circular path.
Example – The whirling motion of a stone attached to a string.

Question 5.
What is rotational motion? Give example.
Answer:
During a motion every point in the object traverses a circular path about an axis except the points located on the axis, is called as rotational motion.
Example – Spinning of the earth about its own axis.

Question 6.
What is vibratory motion? Give example.
Answer:
If an object or particle executes a to and fro motion about a fixed point, it is said to be in vibratory motion.
Example – Vibration of a string on a guitar.

Question 7.
What is one dimensional motion? Give example.
Answer:
One dimensional motion is the motion of a particle moving along a straight line.
Example –  Motion of a train along a straight railway track.

Question 8.
What is two dimensional motion? Give example.
Answer:
If a particle moving along a curved path in a plane, then it is said to be in two dimensional motion.
Example – Motion of a coin on a carrom board.

Question 9.
What is three dimensional motion? Give example.
Answer:
If a particle moving in used three dimensional space, then the particle is said to be in three dimensional motion.
E.g. A bird flying in the sky.

Question 10.
Write about the properties of components of vectors.
Answer:
If two vectors \(\overline{\mathrm{A}}\) and \(\overline{\mathrm{B}}\) are equal, then their individual components are also equal. then their individual components are also equal.
Let\(\overline{\mathrm{A}}\) = \(\overline{\mathrm{B}}\)
then A_x  \(\hat{i}\) + A_y \(\hat{j}\) + A_z \(\hat{k}\) = B_x \(\hat{i}\) + B_y \(\hat{j}\) + B_z \(\hat{k}\)
i.e. A_x = B_x, A_y =  B_y  = A_z = B_z

Question 11.
Give an example for scalar product of two vectors.
Answer:
The work done by a force \(\overrightarrow{\mathrm{F}}\) to move an object through a small displacement \(\overrightarrow{\mathrm{dr}}\) then
Work done W = \(\overrightarrow{\mathrm{F}}\) .\(\overrightarrow{\mathrm{dr}}\) (or) W = F dr cos θ

Question 12.
Give any three example for vector product of two vectors.
Answer:

1. Torque \(\overrightarrow{\mathrm{t}}\) = \(\overrightarrow{\mathrm{r}}\) x \(\overrightarrow{\mathrm{F}}\). Where i is force and \(\overrightarrow{\mathrm{F}}\) is force and \(\overrightarrow{\mathrm{r}}\) position vector of a particle.
2. Angular momentum \(\overrightarrow{\mathrm{L}}\) = \(\overrightarrow{\mathrm{r}}\) x \(\overrightarrow{\mathrm{P}}\) where \(\overrightarrow{\mathrm{P}}\) is the linear momentum.
3. Linear velocity \(\overrightarrow{\mathrm{v}}\) = \(\overrightarrow{\mathrm{ω}}\) x \(\overrightarrow{\mathrm{r}}\) where \(\overrightarrow{\mathrm{ω}}\) is angular velocity.

Question 13.
What is position vector?
Answer:
It is vector which denotes the position of a particle at any instant of time, with respect to some reference frame or coordinate system.
The position \(\overrightarrow{\mathrm{r}}\) vector of the particle at a point P is given by
\(\overrightarrow{\mathrm{r}}\) = x\(\hat{i}\) + y\(\hat{j}\) + z\(\hat{k}\)
where x, y and z are components of \(\overrightarrow{\mathrm{r}}\).

Question 14.
Write a note an momentum.
Answer:
Momentum of a particle is defined as product of mass with velocity. It is denoted as \(\overrightarrow{\mathrm{p}}\) Momentum is also a vector quantity
\(\overrightarrow{\mathrm{r}}\) = m\(\overrightarrow{\mathrm{v}}\)
The direction of momentum is also in the direction of velocity, and the magnitude of momentum is equal to product of mass and speed of the particle.
p = mv
In component form the momentum can be written as
p_x\(\hat{i}\) + p_y\(\hat{j}\)+ p_z\(\hat{k}\) = mv_x\(\hat{i}\) + mv_y\(\hat{j}\) + mv_z\(\hat{k}\)
Here,
p_x = x component of momentum and is equal to mv_x
P_x = y component of momentum and is equal to mv_y
P_x = z component of momentum and is equal to mv_z

Question 15.
“Displacement vector is basically a position vector”. Comment on it.
Answer:
This statement is almost correct only. Because the displacement vector also gives the position of a point just like a position vector. The difference between these two vectors is p. The displacement vector gives the position of a point with respect to a point other than origin but position vector gives the position of a point with respect to origin.

Question 16.
Will two dimensional motion with an acceleration only in one dimension?
Answer:
Yes. In oblique projection, the acceleration is acting vertically downward but the object follows a parabolic path.

Question 17.
A foot ball is kicked by a player with certain angle to the horizontal. Is there any point at which velocity is perpendicular to its acceleration.
Answer:
Yes. At its maximum height in the parabolic path vertical velocity is zero but due to horizontal component, velocity acts along horizontally, but acceleration of the

Question 18.
Give any two examples for parallelogram law of vectors.
Answer:

• the flight of a bird
• working of a sling.

Question 19.
Why does rubber ball bounce greater heights on hills than in plains?
Answer:
The maximum height attained by the projectile is inversely proportional to acceleration due to gravity. At greater height, acceleration due to gravity will be lesser than plains. So ball can bounce higher in hills than in plains.

Question 20.
Is it possible for body to have variable velocity but constant speed? Give example.
Answer:
Yes, it is possible. In horizontal circular motion the speed of a particle is always constant but due to the variation in direction continuously, the velocity of a particle varies.

Question 21.
What is relative velocity?
Answer:
When two objects are moving with different velocities, then the velocity of one object with respect to another object is called relative velocity of an object with respect to another.

Question 22.
What is average acceleration?
Answer:
The average acceleration is defined as the ratio of change in velocity over the time interval
a_avg = \(\frac{\Delta \overrightarrow{\mathrm{v}}}{\Delta t}\) It is a vector quantity.

Question 23.
Write a note an instantaneous acceleration.
Answer:
Instantaneous acceleration or acceleration of a particle at time ‘t’ is given by the ratio of change in velocity over ∆t, as ∆t approaches zero.
Acceleration
In other words, the acceleration of the particle at an instant t is equal to rate of change of velocity

(1) Acceleration is a vector quantity. Its SI unit is ms^-2 and its dimensional formula is [M°L¹ T^-2]

(2) Acceleration is positive if its velocity is increasing, and is negative if the velocity is decreasing. The negative acceleration is called retardation or deceleration.

Question 24.
Write an acceleration in terms of its component?
(Or)
Show that the acceleration is the second derivative of position vector with respect to time.
Answer:
in terms of components, we can write,


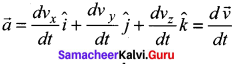
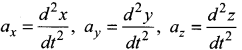
are the components of instantaneous acceleration. Since each component of velocity is the derivative of the corresponding coordinate, we can express the components a_x, a_y, and a_z as

Then the acceleration vector \(\overrightarrow{\mathrm{a}}\) it self is

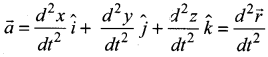
Thus acceleration is the second derivative of position vector with respect to time.

This is free online projectile motion calculator. enter velocity and time value then click on calculate and result will be instant displayed ,this calculator.

Question 25.
What are the examples of projectile motion?
Answer:

1. An object dropped from window of a moving train.
2. A bullet fired from a rifle.
3. A ball thrown in any direction.
4. A javelin or shot put thrown by an athlete.
5. A jet of water issuing from a hole near the bottom of a water tank.

Question 26.
Explain projectile motion.
Answer:
A projectile moves under the combined effect of two velocities.

• A uniform velocity in the horizontal direction, which will not change provided there is no air resistance.
• A uniformly changing velocity (i.e., increasing or decreasing) in the vertical direction.

There are two types of projectile motion:

• Projectile given an initial velocity in the horizontal direction (horizontal projection)
• Projectile given an initial velocity at an angle to the horizontal (angular projection)

To study the motion of a projectile, let us assume that,

• Air resistance is neglected.
• The effect due to rotation of Earth and curvature of Earth is negligible.
• The acceleration due to gravity is constant in magnitude and direction at all points of the motion of the projectile.

Question 27.
What is time of flight?
Answer:
The time taken for the projectile to complete its trajectory or time taken by the projectile to hit the ground is called time of flight.

Question 28.
Under what condition is the average velocity equal the instantaneous velocity?
Answer:
When the body is moving with uniform velocity.

Question 29.
Draw Position time graph of two objects, A & B moving along a straight line, when their relative velocity is zero.

Question 30.
Suggest a situation in which an object is accelerated and have constant speed.
Answer:
Uniform Circular Motion.

Question 31.
Two balls of different masses are thrown vertically upward with same initial velocity. Maximum heights attained by them are h₁ and h₂ respectively what is h₁/h₂?
Answer:
Same height,
∴  h₁/h₂ = 1

Question 32.
A car moving with velocity of 50 kmh^-1 on a straight road is ahead of a jeep moving with velocity 75 kmh^-1 would the relative velocity be altered if jeep is ahead of car?
Answer:
No change.

Question 33.
Which of the two – linear velocity or the linear acceleration gives the direction of motion of a body?
Answer:
Linear velocity.

Question 34.
Will the displacement of a particle change on changing the position of origin of the coordinate system?
Answer:
Will not change.

Question 35.
If the instantaneous velocity of a particle is zero, will its instantaneous acceleration be necessarily zero?
Answer:
No. (highest point of vertical upward motion under gravity).

Question 36.
A projectile is fired with Kinetic energy 1 KJ. If the range is maximum, what is its Kinetic energy, at the highest point?
Answer:
Here \(\frac { 1 }{ 2 }\) mv² =1kJ=1000 J, θ = 45°
At the highest point, K.E. = \(\frac { 1 }{ 2 }\) m(v cos 0)² = \(\frac { 1 }{ 2 }\)\(\frac{m v^{2}}{2}\) = \(\frac {1000}{ 2 }\) = 500 J.

Question 37.
Write an example of zero vector.
Answer:
The velocity vectors of a stationary object is a zero vectors.

Question 38.
State the essential condition for the addition of vectors.
Answer:
They must represent the physical quantities of same native.

Question 39.
When is the magnitude of (\(\overline{\mathrm{A}}\) + \(\overline{\mathrm{B}}\)) equal to the magnitude of (\(\overline{\mathrm{A}}\) – \(\overline{\mathrm{B}}\))?
Answer:
When \(\overline{\mathrm{A}}\) is perpendicular to \(\overline{\mathrm{B}}\).

Question 40.
What is the maximum number of component into which a vector can be resolved?
Answer:
Infinite.

Question 41.
A body projected horizontally moves with the same horizontal velocity although it moves under gravity Why?
Answer:
Because horizontal component of gravity is zero along horizontal direction.

Question 42.
What is the angle between velocity and acceleration at the highest point of a projectile motion?
Answer:
90°.

Question 43.
When does

• height attained by a projectile maximum?
• horizontal range is maximum?

Answer:

• Height is maximum at θ = 90
• Range is maximum at θ = 45.

Question 44.
What is the angle between velocity vector and acceleration vector in uniform circular motion?
Answer:
90°.

Question 45.
A particle is in clockwise uniform circular motion the direction of its acceleration is radially inward. If sense of rotation or particle is anticlockwise then what is the direction of its acceleration?
Answer:
Radial in ward.

Question 46.
A train is moving on a straight track with acceleration a. A passenger drops a stone. What is the acceleration of stone with respect to passenger?
Answer:
\(\sqrt{a^{2}+g^{2}}\) where g = acceleration due to gravity.

Question 47.
What is the average value of acceleration vector in uniform circular motion over one cycle?
Answer:
Null vector.

Question 48.
Does a vector quantity depends upon frame of reference chosen?
Answer:
No.

Question 49.
What is the angular velocity of the hour hand of a clock?
Answer:
ω = \(\frac {2π}{ 12 }\) = \(\frac { π }{6}\) rad h^-1

Question 50.
What is the source of centripetal acceleration for earth to go round the sun?
Answer:
Gravitation force of sun.

Question 51.
What is the angle between (\(\overrightarrow{\mathrm{A}}\) + \(\overrightarrow{\mathrm{A}}\) ) and (\(\overrightarrow{\mathrm{A}}\) – \(\overrightarrow{\mathrm{A}}\)) ?
Answer:
90°

Samacheer Kalvi 11th Physics Kinematics Short Answer Questions – II (2 Marks)

Question 1.
What are positive and negative acceleration in straight line motion?
Solution:
If speed of an object increases with time, its acceleration is positive. (Acceleration is in the direction of motion) and if speed of an object decreases with time its acceleration is negative (Acceleration is opposite to the direction of motion).

Question 2.
Can a body have zero velocity and still be accelerating? If yes gives any situation.
Solution:
Yes, at the highest point of vertical upward motion under gravity.

Question 3.
The displacement of a body is proportional to t³, where t is time elapsed. What is the nature of acceleration –  time graph of the body?
Solution:
As a α t³ ⇒ s = kt³
Velocity, V = \(\frac { ds }{ dt }\) = 3 kt³
Acceleration, a = \(\frac { dv }{ dt }\) = 3 kt³
i.e., a α t
⇒ motion is uniform, acceleration motion, a – t graph is straight-line.

Question 4.
Suggest a suitable physical situation for the following graph.

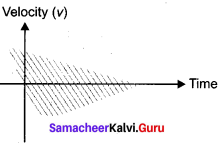
Solution:
A ball thrown up with some initial velocity rebounding from the floor with reduced speed after each hit.

Question 5.
An object is in uniform motion along a straight line, what will be position time graph for the motion of object, if (i) x₀ = positive, v = negative is constant.
(i) x₀ = positive, v = negative is |\(\vec{v}\) | constant.
(ii) both x₀ and v are negative |\(\vec{v}\) | is constant.
(iii) x₀ = negative, v = positive |\(\vec{v}\) | is constant.
(iv) both x₀ and v are positive |\(\vec{v}\) | is constant where x₀ is position at t = 0.
Solution:

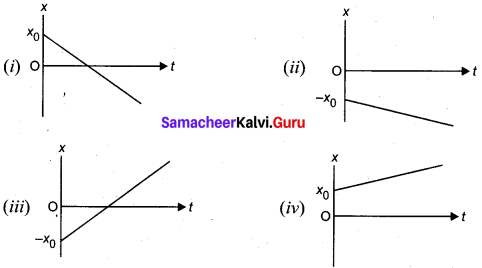
Question 6.
A cyclist starts from centre O of a circular park of radius 1 km and moves along the path OPRQO as shown. If he maintains constant speed of 10 ms^-1. What is his acceleration at point R in magnitude & direction?

Solution:
Centripetal acceleration, a_c = \(\frac{v^{2}}{r}\) = \(\frac{10^{2}}{1000}\) = 0.1 m/s² along RO.

Question 7.
What will be the effect on horizontal range of a projectile when its initial velocity is doubled keeping angle of projection same?
Solution:
\(\frac{u^{2} \sin 2 \theta}{g}\) ⇒ R α u²
Range comes four times.

Question 8.
The greatest height to which a man can throw a stone is h. What will be the greatest distance upto which he can throw the stone?
Solution:
Maximum height:
H = \(\frac{u^{2} \sin ^{2} \theta}{g}\) ⇒ H_max = \(\frac{u^{2}}{2g}\) = h (at θ = 90)
Maximum range R_max = \(\frac{u^{2}}{g}\) = 2h

Question 9.
A person sitting in a train moving at constant velocity throws a ball vertically upwards. How will the ball appear to move to an observer.

• Sitting inside the train
• Standing outside the train

Solution:

• Vertical straight line motion
• Parabolic path.

Question 10.
A gunman always keep his gun slightly tilted above the line of sight while shooting. Why?
Solution:
Because bullet follow Parabolic trajectory under constant downward acceleration.

Question 11.
Is the acceleration of a particle in circular motion not always towards the center. Explain.
Solution:
No acceleration is towards the center only in case of uniform circular motion.

Samacheer Kalvi 11th Physics Kinematics Short Answer Questions – III (3 Marks)

Question 1.
Draw
(a) acceleration – time
(b) velocity – time
(c) Position – time graphs representing motion of an object under free fall. Neglect air resistance.
Solution:
The object falls with uniform acceleration equal to ‘g’

Question 2.
The velocity time graph for a particle is shown in figure. Draw acceleration time graph from it.

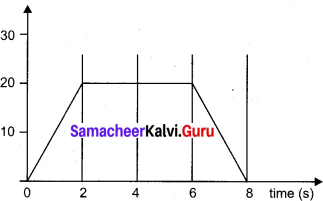
Solution:

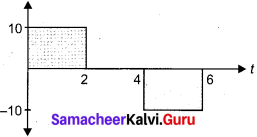
Question 3.
For an object projected upward with a velocity v₀, which comes back to the same point after some time, draw
(i) Acceleration – time graph
(ii) Position – time graph
(iii) Velocity time graph
Solution:

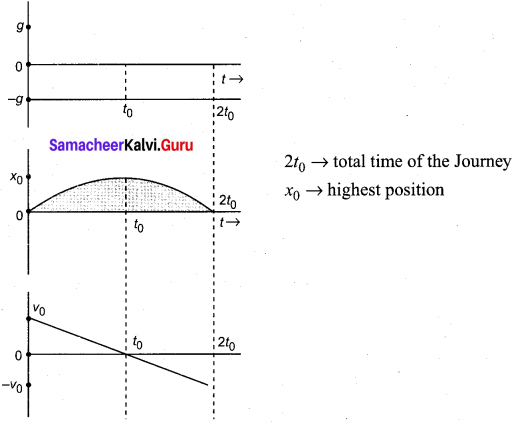
Question 4.
The acceleration of a particle in ms² is given by a = 3t² + 2t + 2, where time t is in second. If the particle starts with a velocity v = 2 ms^-1 at t = 0, then find the velocity at the end of 2s.
Solution:

Question 5.
At what angle do the two forces (P + Q) and (P – Q) act so that the resultant is \(\sqrt{3 P^{2}+Q^{2}}\)?
Solution:
Use
R = \(\sqrt{3 P^{2}+Q^{2}}\)
R = \(\sqrt{3 \mathrm{P}^{2}+\mathrm{Q}^{2}}\)
A = P + Q
B = P – Q
solve, θ = 60°

Question 6.
A car moving along a straight highway with speed of 126 km h 1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform) and how long does it take for the car to stop?
Solution:
Initial velocity of car,
u = 126 kmh^-1 = 126 x \(\frac {5}{18}\) ms^-1 = 35 ms^-1 ………(i)
Since, the car finally comes to rest, v = 0
Distance covered, s = 200 m, a = ?, t = ?
v² = u² – 2as
or a = \(\frac{v^{2}-u^{2}}{2 s}\) ………..(ii)
substituting the values from eq. (i) in eq . (ii), we get
a = \(\frac{0-(35)^{2}}{2 \times 200}\) = \(\frac{0-(35)^{2}}{2 \times 200}\)
= \(-\frac{46}{16}\) ms^-2 = -3.06 ms^-2
Negative sign shows that acceleration in negative which is called retardation, i.e., car is uniformly retarded at – a = 3.06 ms^-2.
To find t, let us use the relation
v = u + at
t = \(\frac {v-u}{ a }\)
use a = -3.06 ms^-2, v = 0, u = 35 ms^-1
∴ t = \(\frac {v-u}{ a }\) = \(\frac {0-35}{ -3.06 }\) = 11.44 s
∴ t = 11.44 sec

Samacheer Kalvi 11th Physics Kinematics Long Answer Questions
Question 1.
Explain the types of motion with example.
Answer:
(a) Linear motion:
An object is said to be in linear motion if it moves in a straight line.
Examples:

• An athlete running on a straight track
• AA particle falling vertically downwards to the Earth.

(b) Circular motion:
Circular motion is defined as a motion described by an object traversing a circular path.
Examples:

• The whirling motion of a stone attached to a string.
• The motion of a satellite around the Earth.
• These two circular motions are shown in figure.

(c) Rotational motion:
If any object moves in a rotational motion about an axis, the motion is called ‘rotation’. During rotation every point in the object transverses a circular path about an axis, (except the points located on the axis).
Examples:

• Rotation of a disc about an axis through its center
• Spinning of the Earth about its own axis.
• These two rotational motions are shown in figure

(d) Vibratory motion:
If an object or particle executes a to-and-fro motion about a fixed point, it is said to be in vibratory motion. This is sometimes also called oscillatory motion.
Examples:

• Vibration of a string on a guitar
• Movement of a swing
• These motions are shown in figure

Other types of motion like elliptical motion and helical motion are also possible.

Question 2.
What are the different types of vectors? ,
Answer:
1. Equal vectors:
Two vectors A and B are said to be equal when they have equal magnitude and same direction and represent the same physical quantity

(a) Collinear vectors:
Col-linear vectors are those which act along the same line. The angle between them can be 0° or 180°.

(i) Parallel vectors:
If two vectors A and B act in the same direction along the same line or on parallel lines, then the angle between them is 0°. Geometrical representation of parallel vectors.

(ii) Anti-parallel vectors:
Two vectors A and B are said to be anti – parallel when they are in opposite directions along the same line or on parallel lines. Then the angle between them is 180°.

2. Unit vector:
A vector divided by its magnitude is a unit vector. The unit vector for \(\overrightarrow{\mathrm{A}}\) is denoted by \(\widehat{A}\) . It has a magnitude equal to unity or one.
Since, \(\widehat{A}\) = \(\frac{\bar{A}}{A}\) we can write \(\overrightarrow{\mathrm{A}}\) = A\(\widehat{A}\)
Thus, we can say that the unit vector specifies only the direction of the vector quantity.

3. Orthogonal unit vectors:
Let \(\hat{i}\), \(\hat{j}\) and \(\hat{k}\) be three unit vectors which specify the directions along positive x-axis, positive y-axis and positive z-axis respectively. These three unit vectors are directed perpendicular to each other, the angle between any two of them is 90°.\(\hat{i}\), \(\hat{j}\) and \(\hat{k}\) and are examples of orthogonal vectors. Two vectors which are perpendicular to each other are called orthogonal vectors as shown in the figure.

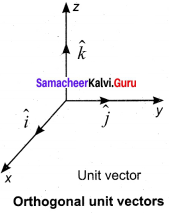
Question 3.
Explain the concept of relative velocity in one and two dimensional motion.
Answer:
When two objects A and B are moving with different velocities, then the velocity of one object A with respect to another object B is called relative velocity of object A with respect to B.

Case I:
Consider two objects A and B moving with uniform velocities V_A and V_B, as shown, along straight tracks in the same direction \(\overrightarrow{\mathrm{V}}_{\mathrm{A}}\), \(\overrightarrow{\mathrm{V}}_{\mathrm{B}}\) with respect to ground.
The relative velocity of object A with respect to object B is \(\overrightarrow{\mathrm{V}}_{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{V}}_{\mathrm{A}}\) – \(\overrightarrow{\mathrm{V}}_{\mathrm{B}}\).
The relative velocity of object B with respect to object A is \(\overrightarrow{\mathrm{V}}_{\mathrm{BA}}\) = \(\overrightarrow{\mathrm{V}}_{\mathrm{B}}\) – \(\overrightarrow{\mathrm{V}}_{\mathrm{A}}\) Thus, if two objects are moving in the same direction, the magnitude of relative velocity of one object with respect to another is equal to the difference in magnitude of two velocities.

Case II.
Consider two objects A and B moving with uniform velocities \(\overrightarrow{\mathrm{V}}_{\mathrm{A}}\) and \(\overrightarrow{\mathrm{V}}_{\mathrm{B}}\) along the same straight tracks but opposite in direction.

The relative velocity of an object A with respect to object B is –
\(\overrightarrow{\mathrm{V}}_{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{V}}_{\mathrm{A}}\) – (-\(\overrightarrow{\mathrm{V}}_{\mathrm{B}}\)) = \(\overrightarrow{\mathrm{V}}_{\mathrm{A}}\) + \(\overrightarrow{\mathrm{V}}_{\mathrm{B}}\)

The relative velocity of an object B with respect to object A is
\(\overrightarrow{\mathrm{V}}_{\mathrm{AB}}\) = –\(\overrightarrow{\mathrm{V}}_{\mathrm{A}}\) – \(\overrightarrow{\mathrm{V}}_{\mathrm{A}}\) = – (\(\overrightarrow{\mathrm{V}}_{\mathrm{A}}\) + \(\overrightarrow{\mathrm{V}}_{\mathrm{B}}\))
Thus, if two objects are moving in opposite directions, the magnitude of relative velocity of one object with respect to other is equal to the sum of magnitude of their velocities.

Case III.
Consider the velocities \(\overrightarrow{\mathrm{v}}_{\mathrm{A}}\) and \(\overrightarrow{\mathrm{v}}_{\mathrm{B}}\) at an angle θ between their directions. The relative velocity of A with respect to B, \(\overrightarrow{\mathrm{v}}_{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{v}}_{\mathrm{A}}\) – \(\overrightarrow{\mathrm{v}}_{\mathrm{B}}\)
Then, the magnitude and direction of \(\overrightarrow{\mathrm{v}}_{\mathrm{AB}}\) is given by \(\overrightarrow{\mathrm{v}}_{\mathrm{AB}}\) = \(\sqrt{\vec{v}_{\mathrm{A}}^{2}+\vec{v}_{\mathrm{B}}^{2}-2 v_{\mathrm{A}} v_{\mathrm{B}} \cos \theta}\) and tan β = \(\frac{v_{\mathrm{B}} \sin \theta}{v_{\mathrm{A}}-v_{\mathrm{B}} \cos \theta}\) (Here β is angle between (\(\overrightarrow{\mathrm{v}}_{\mathrm{B}}\) and \(\overrightarrow{\mathrm{v}}_{\mathrm{A}}\))
\(\overrightarrow{\mathrm{v}}_{\mathrm{A}}\) – \(\overrightarrow{\mathrm{v}}_{\mathrm{B}}\) cos θ .

(i) When θ = 0, the bodies move along parallel straight lines in the same direction, We have \(\overrightarrow{\mathrm{v}}_{\mathrm{AB}}\) = (\(\overrightarrow{\mathrm{v}}_{\mathrm{A}}\) – \(\overrightarrow{\mathrm{v}}_{\mathrm{B}}\)) in the direction of \(\overrightarrow{\mathrm{v}}_{\mathrm{A}}\) . Obviously \(\overrightarrow{\mathrm{v}}_{\mathrm{BA}}\) = (\(\overrightarrow{\mathrm{v}}_{\mathrm{B}}\) + \(\overrightarrow{\mathrm{v}}_{\mathrm{A}}\)) in the direction of \(\overrightarrow{\mathrm{v}}_{\mathrm{B}}\).

(ii) When θ = 180°, the bodies move along parallel straight lines in opposite directions,
We have \(\overrightarrow{\mathrm{v}}_{\mathrm{AB}}\) = (\(\overrightarrow{\mathrm{v}}_{\mathrm{A}}\)+ \(\overrightarrow{\mathrm{v}}_{\mathrm{B}}\)) in the direction of \(\overrightarrow{\mathrm{v}}_{\mathrm{A}}\) . Similarly, vBA = (vB + vA) in the direction of \(\overrightarrow{\mathrm{v}}_{\mathrm{B}}\) .

(iii) If the two bodies are moving at right angles to each other, then 0 = 90°. The magnitude of the relative velocity of A with respect to B = \(\overrightarrow{\mathrm{v}}_{\mathrm{AB}}\) = \(\sqrt{v_{\mathrm{A}}^{2}+v_{\mathrm{B}}^{2}}\).

(iv) Consider a person moving horizontally with velocity \(\overrightarrow{\mathrm{V}}_{\mathrm{M}}\) . Let rain fall vertically with velocity \(\overrightarrow{\mathrm{V}}_{\mathrm{R}}\) . An umbrella is held to avoid the rain. Then the relative velocity of the rain with respect to the person is,

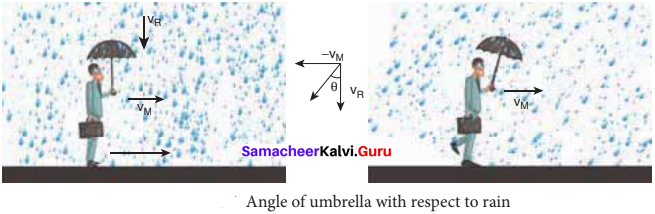
which has magnitude
\(\overrightarrow{\mathrm{V}}_{\mathrm{RM}}\) = \(\overrightarrow{\mathrm{V}}_{\mathrm{R}}\) – \(\overrightarrow{\mathrm{V}}_{\mathrm{M}}\)
And direction 0 = tan^-1\(\left(\frac{V_{\mathrm{M}}}{\mathrm{V}_{\mathrm{R}}}\right)\) with the vertical as shown in figure.

Question 4.
Shows that the path of horizontal projectile is a parabola and derive an expression for
1. Time of flight
2. Horizontal range
3. resultant relative and any instant
4. speed of the projectile when it hits the ground?
Answer:
Consider a projectile, say a ball, thrown horizontally with an initial velocity \(\vec{u}\) from the top of a tower of height h. As the ball moves, it covers a horizontal distance due to its uniform horizontal velocity u, and a vertical downward distance because of constant acceleration due to gravity g. Thus, under the combined effect the ball moves along the path OPA. The motion is in a 2 – dimensional plane. Let the ball take time t to reach the ground at point A, Then the horizontal distance travelled by the ball is x(t) = x, and the vertical distance travelled is y(t) = y.

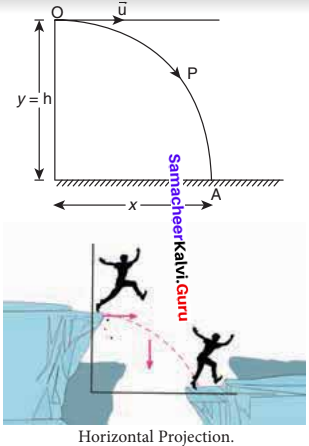
We can apply the kinematic equations along the x direction and y direction separately. Since this is two-dimensional motion, the velocity will have both horizontal component u_x and vertical component u_y.

Motion along horizontal direction:
The particle has zero acceleration along x direction. So, the initial velocity ux remains constant throughout the motion. The distance traveled by the projectile at a time t is given by the equation x = u_xt +\(\frac { 1 }{ 2 }\) at² . Since a = 0 along x direction, we have x = u_xt ……….(1)

Motion along downward direction:
Here u_y = 0 (initial velocity has no downward component), a = g (we choose the + ve y – axis in downward direction), and distance y at time t.
From equation, y = u_xt +\(\frac { 1 }{ 2 }\) at² we get
y = \(\frac { 1 }{ 2 }\) at² …………..(2)

Substituting the value oft from equation (i) in equation (ii) we have

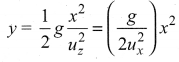
y = Kx²
where K = \(\frac{g}{2 u_{x}^{2}}\) is constant
Equation (iii) is the equation of a parabola. Thus, the path followed by the projectile is a parabola.

1. Time of Flight:
The time taken for the projectile to complete its trajectory or time taken by the projectile to hit the ground is called time of flight. Consider the example of a tower and projectile. Let h be the height of a tower. Let T be the time taken by the projectile to hit the ground, after being thrown horizontally from the tower.

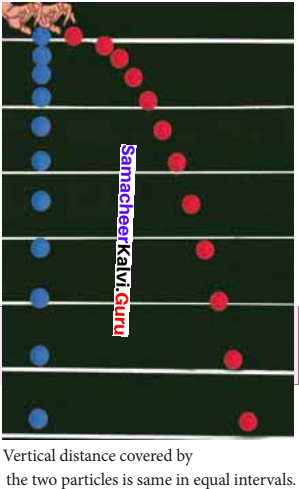
We know that s_y = u_yt + \(\frac { 1 }{ 2 }\) at² for vertical motion. Here .s_y = h, t = T, u_y = 0 (i.e., no initial vertical velocity). Then h = \(\frac { 1 }{ 2 }\) gt² or T = \(\sqrt{\frac{2 h}{g}}\) Thus, the time of flight for projectile motion depends on the height of the tower, but is independent of the horizontal velocity of projection. If one ball falls vertically and another ball is projected horizontally with some velocity, both the balls will reach the bottom at the same time. This is illustrated in the Figure

2. Horizontal range:
The horizontal distance covered by the projectile from the foot of the tower to the point where the projectile hits the ground is called horizontal range.
For horizontal motion, we have
s_x = u_xt + \(\frac { 1 }{ 2 }\) at²
Here,s_x = R (range), u_x = u, a = 0 (no horizontal acceleration) T is time of flight. Then horizontal range = uT
Since the time of flight T = \(\sqrt{\frac{2 h}{g}}\) we substitute this and we get the horizontal range of the particle as R = u \(\sqrt{\frac{2 h}{g}}\)
The above equation implies that the range R is directly proportional to the initial velocity u and inversely proportional to acceleration due to gravity g.

3. Resultant Velocity (Velocity of projectile at any time):
At any instant t, the projectile has velocity components along both x-axis and y-axis. The resultant of these two components gives the velocity of the projectile at that instant t, as shown in figure. The velocity component at any t along horizontal (x-axis)
is V_x = U_x + a_xt
Since, u_x = u, ax = 0 , we get
u_x = u a_x = 0 we get
v_x = u
The component of velocity along vertical direction (y – axis) is v_y = u_y + a_yt
Since, u_y= 0, a_y = g, we get
V_y = gt
Hence the velocity of the particle at any instant is –
v = u\(\hat{i}\) + g\(\hat{j}\)
The speed of the particle at any instant t is given by
v = \(\sqrt{v_{x}^{2}+v_{y}^{2}}\)
v= \(\sqrt{u^{2}+g^{2} t^{2}}\)

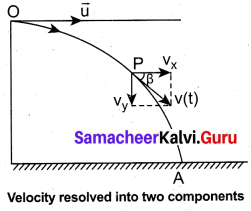
4. Speed of the projectile when it hits the ground:
When the projectile hits the ground after initially thrown horizontally from the top of tower of height h, the time of flight is –
t = \(\sqrt{\frac{2 h}{g}}\)
The horizontal component velocity of the projectile remains the same i.e v_x = u.
The vertical component velocity of the projectile at time T is
v = gT = g \(\sqrt{\frac{2 h}{g}}\) = \(\sqrt{\frac{2gh}\)
The speed of the particle when it reaches the ground is
v = \(\sqrt{u^{2}+2 g h}\).

Question 5.
Derive the relation between Tangential acceleration and angular acceleration.
Answer:
Consider an object moving along a circle of radius r. In a time ∆t, the object travels in an arc distance As as shown in figure. The corresponding angle subtended is ∆θ
The ∆s can be written in terms of ∆θ
∆s = r∆θ ………(i)
in a time ∆t, we have
\(\frac { ∆s }{ ∆t}\) = t \(\frac { ∆θ }{ ∆t}\) …………(ii)
¡n the limit ∆t – 0, the above equation becomes
\(\frac { ds }{ dt}\) = rω …………….(iii)
Here \(\frac { ds }{ dt}\) is linear speed (y) which is tangential to the circle and co is angular speed.
So equation (iii) becomes.
v _r = rω …….(iv)

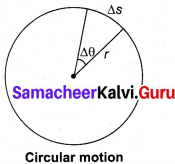
which gives the relation between linear speed and angular speed.
Eq. (iv) is true only for circular motion. In general the relation between linear and angular velocity is given by
\(\vec{v}\) = \(\vec{\omega} \times \vec{r}\) ………..(v)
For circular motion eq. (y) reduces to eq. (iv) since \(\overrightarrow{\mathrm{ω}}\) and \(\overrightarrow{\mathrm{r}}\)are perpendicular to each other.
Differentiating the eq. (iv) with respect to time, we get (since r is constant)
\(\frac { dv }{ dt}\) = \(\frac { rdv }{ dt}\) = rα
Here \(\frac { dv }{ dt}\) Is the tangential acceleration and is denoted as a_t = \(\frac {dω}{ dt}\)is the angular acceleration
α. Then eq. (v) becomes
a_t = rα ………..(vii)

Samacheer Kalvi 11th Physics Kinematics Numerical Questions

Question 1.
The V – t graphs of two objects make angle 30° and 60° with the time axis. Find the ratio of their accelerations.
Solution:
\(\frac{a_{1}}{a_{2}}\) = \(\frac{tan 30}{tan 60}\) = \(\frac{1 / \sqrt{3}}{\sqrt{3}}\) = \(\frac{1}{3}\) = 1 : 3.

Question 2.
When the angle between two vectors of equal magnitudes is 2n/?>, prove that the magnitude of the resultant is equal to either.
Solution:
R = \(\left(\mathrm{P}^{2}+\mathrm{Q}^{2}+2 \mathrm{PQ} \cos \theta\right)^{1 / 2}\) = \(\left(p^{2}+p^{2}+2 p \cdot p \cos \frac{2 \pi}{3}\right)\) = \(\left[2 p^{2}+2 p^{2}\left(\frac{-1}{2}\right)\right]^{1 / 2}\) = p.

Question 3.
If \(\overline{\mathrm{A}}\) = 3\(\hat{i}\) + 4\(\hat{j}\) and \(\overline{\mathrm{B}}\) = 7\(\hat{i}\) + 24 \(\hat{j}\), find a vector having the same magnitude as \(\overline{\mathrm{B}}\) and parallel to \(\overline{\mathrm{A}}\).
Solution:
\(|\overrightarrow{\mathrm{A}}|=\sqrt{3^{2}+4^{2}}=5\)
also \(|\overrightarrow{\mathrm{B}}|=\sqrt{7^{2}+24^{2}}=25\)
desired vector = \(|\overrightarrow{\mathrm{B}}|\) \(\widehat{A}\) = 25 x \(\frac{3 \hat{i}+4 \hat{j}}{5}\) = 5(3\(\hat{j}\) + 4\(\hat{j}\)) = 15 \(\hat{i}\) + 20\(\hat{j}\).

Question 4.
What is the vector sum of n coplanar forces, each of magnitude F, if each force makes an angle of \(\frac {2 π}{ n }\) with the preceding force?
Solution:
Resultant force is zero.

Question 5.
A car is moving along X- axis. As shown in figure it moves from O to P in 18 seconds and return from P to Q in 6 second. What are the average velocity and average speed of the car in going from

• O to P
• From O to P and hack to Q

Solution:

• O to P, Average velocity =20 ms^-1
• O to P and back to Q

Average velocity = 10 ms^-1
Average speed = 20 ms^-1

Question 6.
On a 60 km straight road, a bus travels the first 30 km with a uniform speed of 30 kmh^-1 . How fast must the bus travel the next 30 km so as to have average speed of 40 kmh^-1 for the entire trip?
Solution:

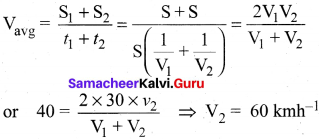
Question 7.
The displacement x of a particle varies with time as x = 4t² – 15t + 25. Find the position, velocity and acceleration of the particle at t = O.
Solution:
Position, x = 25 m
Velocity = \(\frac { dx}{dt}\)8t – 15
t = 0, v = 0 – 15 = -15 m/s
acceleration, a = \(\frac { dx}{dt}\) = 8 ms^-2

Question 8.
A driver takes 0.20 second to apply the breaks (reaction time). If he is driving car at a speed of 54 kmh^-1 and the breaks cause a deceleration of 6.0 ms^-2. Find the distance travelled by car after he sees the need to put the breaks.
Solution:
(distance covered during 0.20 s) + (distance covered until rest)
= (15 x 0.25) + [18.75] = 21.75 m.

Question 9.
From the top of a tower 100 m in height a ball is dropped and at the same time another ball is projected vertically upwards from the ground with a velocity of 25 m/s. Find when and where the two balls will meet? (g = 9.8 m/s)
Solution:
For the ball dropped from the top
x = 4.9 t²…….(i)
For the ball thrown upwards
100 – x =25t – 4.9 t² …….(ii)
From eq. (i) and (ii)
t = 4s  x = 78.4 m.

Question 10.
A ball thrown vertically upwards with a speed of 19.6 ms^-1 from the top of a tower returns to the earth in 6s. Find the height of the tower, (g = 9.8 m/s)
Solution:
s = ut + \(\frac { 1 }{ 2 }\) at²
-h = 19. 6 x 6 + \(\frac { 1 }{ 2 }\) x (-9.8) x (6)²
h = 58.8 m.

Question 11.
Two town A and B are connected by a regular bus service with a bus leaving in either direction every T min. A man cycling with a speed of 20 kmh^-1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed do the buses ply of the road?
Solution:
V =40 krnh^-1 and T = 9 min.

Question 12.
A motorboat is racing towards north at 25 kmh^-1 and the water current in that region is 10 kmh^-1 in the direction of 60° east of south. Find the resultant velocity of the boat.
Solution:
V= 21.8 kmh^-1
angle with north, θ = 23.4°.

Question 13.
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft position 10 second apart is 30°, what is the speed of the aircraft?
Solution:
Speed = 182.2 ms^-1

Question 14.
A boat is moving with a velocity (3\(\hat{i}\) -4\(\hat{j}\)) with respect to ground. The water in river is flowing with a velocity (-3\(\hat{i}\) – 4\(\hat{j}\)) with respect to ground. What is the relative velocity of boat with respect to river?
Solution:
\(\overrightarrow{\mathrm{V}}_{\mathrm{BW}}\)= \(\overrightarrow{\mathrm{V}}_{\mathrm{B}}\).

Question 15.
A hiker stands on the edge of a clift 490 m above the ground and throws a stone horizontally with an initial speed of 15 ms^-1. Neglecting air resistance, find the time taken by the stone to reach the ground and the speed with which it hits the ground. (g 9.8 ms^-2)
Solution:
time = 10 seconds
V = \(\sqrt{\mathrm{V}_{s}^{2}+\mathrm{V}_{Y}^{2}}\) = \(\sqrt{15^{2}+98^{2}}\) = 99.1 m/s^-1

Question 16.
A bullet fired at an angle of 30° with the horizontal hits the ground 3 km away. By adjusting the angle of projection, can one hope to hit the target 5 km away ? Assume that the muzzle speed to be fixed and neglect air resistance.
Solution:
Maximum Range = 3.46 km
So it is not possible.

Question 17.
A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 seconds, what is the magnitude and direction of acceleration of the stone?
Solution:
\(\frac { 88 }{ 25 }\) rad s^-1, \(\frac { 2π}{ T}\) = \(\frac { 2πN}{t}\)
a = 991.2 cm s^-2

Question 18.
A cyclist is riding with a speed of 27 kmh^-1 . As he approaches a circular turn on the road of radius 30 m^-2, he applies brakes and reduces his
speed at the constant rate 0.5 ms^-2. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?
Solution:
a^c = \(\frac{v^{2}}{r}\) = 0.7ms^-2
a^t = 0.5 ms^-2
a = \(\sqrt{a^{2}-a^{2}}\) = 0.86 ms^-2
If O is the angle between the net acceleration and the velocity of the cyclist, then
0= tan^-1 \(\left(\frac{a_{c}}{a_{\mathrm{T}}}\right)\) = tan^-1 = 54°28′

Question 19.
If the magnitude of two vectors are 3 and 4 and their scalar product is 6, find angle between them and also find \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}\)|
Solution:
\(\overrightarrow{\mathrm{A}}\).\(\overrightarrow{\mathrm{B}}\) = AB cos θ
|\(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}\)| = AB sin θ
or 6 = (3 x 4) cos θ = 3 x 4 x 60°
or θ = 60°
= 3 x 4 x \(\frac{\sqrt{3}}{2}\) = \(6 \sqrt{3}\)

Question 20.
Find the value ofA so that the vector \(\overrightarrow{\mathrm{A}}\) = 2 \(\hat{i}\) + \(\hat{j}\) + \(\hat{k}\) and \(\overrightarrow{\mathrm{B}}\) = 4\(\hat{i}\) -2 \(\hat{j}\) +2\(\hat{k}\) are perpendicular to each other.
Solution:
\(\overrightarrow{\mathrm{A}} \perp \overrightarrow{\mathrm{B}}\)
⇒ \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}\)
⇒ t = 3

Question 21.
The velocity time graph of a particle is given by –

•  Calculate distance and displacement of particle from given v – t graph.
• Specify the time for which particle undergone acceleration, retardation and moves with constant velocity.
• Calculate acceleration, retardation from given v – t graph.
• Draw acceleration-time graph of given v – t graph.

Solution:
(i) distance = area of ∆OAB + area of trapezium BCDE = 12 + 28 = 40 m
(ii) displacement area of ∆OAB – area of trapezium BCDE = 12 – 28 = – 16 m

• times acc. \((0 \leq t \leq 4) \) and \((12\leq t \leq 16) \)
• retardation \((4\leq t \leq 8) \)
• constant velocity \((8\leq t \leq 12) \)