Students can Download Physics Chapter 6 Optics Questions and Answers, Notes Pdf, Samacheer Kalvi 12th Physics Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Physics Solutions Chapter 6 Optics
Samacheer Kalvi 12th Physics Optics Textual Evaluation Solved
Samacheer Kalvi 12th Physics Optics Multiple Choice Questions
Question 1.
The speed of light in an isotropic medium depends on,
(a) its intensity
(b) its wavelength
(c) the nature of propagation
(d) the motion of the source w.r.to medium
Answer:
(b) its wavelength
Question 2.
A rod of length 10 cm lies along the principal axis of a concav e mirror of focal length 10 cm in such a way that its end closer to the pole is 20 cm away from the mirror. The length of the image is, (AIPMT Main 2012)
(a) 2.5 cm
(b) 5cm
(c) 10 cm
(d) 15cm
Answer:
(b) 5cm
Hint:
By mirror formula, image distance of A
\(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\) ; \(\frac { { 1 } }{ { v }_{ A } } \) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
\(\frac { { 1 } }{ { v }_{ A } } \) + \(\frac { 1 }{ u }\) + \(\frac { 1 }{ (-30) }\) = \(\frac { 1 }{ (-10) }\)
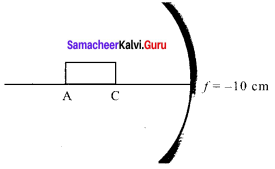
∴ vA = – 15 cm
Image distance of C, vc = – 20 cm
The length of image = |vA – vc|
= |-15 + 20| = 5 cm
The full form of ktm is Kraftfahrzeuge Trunkenpolz Mattighofen. It translates into English to mean “motor Vehicle”.
Question 3.
An object is placed in front of a convex mirror of focal length of/and the maximum and minimum distance of an object from the mirror such that the image formed is real and magnified. (IEE Main 2009)]
(a) 2ƒ and c
(b) c and ∞
(c) ƒ and O
(d) None of these
Answer:
(d) None of these
Hint:
There is no maximum minimum object distance for convex mirror to form real and inverted image.
![]()
Question 4.
For light incident from air onto a slab of refractive index 2. Maximum possible angle of refraction is,
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer:
(a) 30°
Hint:
From Snell’s law, µ = \(\frac { sin i }{ sin r }\)
Now consider an angle of incident is 90°
\(\frac { sin 90° }{ 2 }\)
sin r = sin-1 (0.5)
r = 30°
Question 5.
If the velocity and wavelength of light in air is Va and λa and that in water is Va and λw, then the refractive index of water is,
(a) \(\frac { { V }_{ w } }{ { V }_{ a } } \)
(b) \(\frac { { V }_{ a } }{ { V }_{ w } } \)
(c) \(\frac { { λ }_{ w } }{ { λ }_{ a } } \)
(d) \(\frac { { V }_{ a }{ \lambda } }{ { V }_{ w }{ \lambda }_{ w } } \)
Answer:
(b) \(\frac { { V }_{ a } }{ { V }_{ w } } \)
Question 6.
Stars twinkle due to
(a) reflection
(b) total internal reflection
(c) refraction
(d) polarisation
Answer:
(c) refraction
![]()
Question 7.
When a biconvex lens of glass having refractive index 1.47 is dipped in a liquid, it acts as a plane sheet of glass. This implies that the liquid must have refractive index,
(a) less than one
(b) less than that of glass
(c) greater than that of glass
(d) equal to that of glass
Answer:
(d) equal to that of glass
Hint:
According to len’s maker formula,
\(\frac { 1 }{ ƒ } \) = \(\left(\frac{n_{2}}{n_{1}}-1\right)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\)
Biconvex lens dipped in a liquid, acts as a plane sheet of glass, ƒ = ∞; \(\frac { 1 }{ ƒ } \) = 0
\(\frac { { n }_{ 2 } }{ { n }_{ 1 } } \) -1 = 0; n2 = n1
Question 8.
The radius of curvature of curved surface at a thin planoconvex lens is 10 cm and the refractive index is 1.5. If the plane surface is silvered, then the focal length will be,
(a) 5 cm
(b) 10 cm
(c) 15 cm
(d) 20 cm
Answer:
(b) 10 cm
Hint:
According to len’s maker formula,
\(\frac { 1 }{ ƒ }\) = (n – 1) \(\left( \frac { 1 }{ { R }_{ 1 } } -\frac { 1 }{ { R }_{ 2 } } \right) \)
R1 = ∞; R2 = -6
∴ ƒ = \(\frac { R }{ \left( n – 1 \right) } \) (R= 10 cm; n= 1.5
ƒ = \(\frac { 10}{ \left( 1.5 – 1 \right) } \) =20 cm
Question 9.
An air bubble in glass slab of refractive index 1.5 (near normal incidence) is 5 cm deep when viewed from one surface and 3 cm deep when viewed from the opposite face. The thickness of the slab is,
(a) 8 cm
(b) 10 cm
(c) 12 cm
(d) 16 cm
Answer:
(c) 12 cm
Hint:
Let d1 = 5 cm and d2 = 3 cm ; n = 1.5
Actual width is the sum of real depth from 2 sides
Thickness of slab = d1n + d2 n
= (5 x 1.5) +(3 x 1.5)= 12 cm
Question 10.
A ray of light travelling in a transparent medium of refractive index n falls, on a surface separating the medium from air at an angle of incidents of 45°. The ray can undergo total internal reflection for the following n,
(a) n= 1.25
(b) n = 1.33
(c) n= 1.4
(d) n= 1.5
Answer:
(d) n= 1.5
Hint:
For total internal reflection
sin i > sin c where, i – angle of incidence
But, sin c = 1/n c – critical angle
sin i > 1/n
n > \(\frac { 1 }{ sin i }\)
n > \(\frac { 1 }{ sin 45 }\) ; n > √2 ; n > 1.414
![]()
Question 11.
A plane glass is placed over a various coloured letters (violet, green, yellow, red) The letter which appears to be raised more is,
(a) red
(b) yellow
(c) green
(d) violet
Answer:
(d) violet
Hint:
Letters appear to be raised depending upon the refractive index of the material. Since violet has a higher refractive index than red (the index increases with frequency), red will be the lowermost.
Question 12.
Two point white dots are 1 mm apart on a black paper. They are viewed by eye of pupil diameter 3 mm approximately. The maximum distance at which these dots can be resolved by the eye is, [take wavelength of light, λ = 500 nm]
(a) 1 m
(b) 5 m
(c) 3 m
(d) 6m
Answer:
(b) 5 m
Hint:
Resolution limit sin θ = \(\frac { Y }{ d }\) = \(\frac { 1.22c }{ d }\)

Question 13.
In a Young’s double-slit experiment, the slit separation is doubled. To maintain the same fringe spacing on the screen, the screen-to-slit distance D must be changed to,
(a) 2D
(b) \(\frac { D }{ 2 }\)
(c) √2D
(d) \(\frac { D }{ √2 }\)
Answer:
(a) 2D
Hint:
Young’s double -slite experiment is
β = \(\frac { λD }{ d}\) ; β’ = \(\frac { λD’ }{ d’}\) ; d’ = 2d
Same fringe space, β = β’
⇒ \(\frac { λD }{ d}\) = \(\frac { λD’ }{ d’}\) ; D’ = 2D
Question 14.
Two coherent monochromatic light beams of intensities I and 41 are superposed. The maximum and minimum possible intensities in the resulting beam are [IIT-JEE 1988]
(a) 5I and I
(b) 5I and 3I
(c) 9I and I
(d) 9I and 3I
Answer:
(c) 9I and I
Hint:

Question 15.
When light is incident on a soap film of thickness 5 x 10-5
cm, the wavelength of light reflected maximum in the visible region is 5320 A. Refractive index of the film will be,
(a) 1.22
(b) 1.33
(c) 1.51
(cl) 1.83
Answer:
(b) 1.33
Hint.
The condition for constructive interference, (for reflection)
2µ tcos r = (2n +1) \(\frac { λ }{ 2 }\) [∴ cos r = 1]
µ = \(\frac { \left( 2n+1 \right) \lambda }{ 4t } \)
For visible region, n = 2
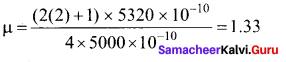
Question 16.
First diffraction minimum due to a single slit of width 1.0 x 10-5 cm is at 30°. Then wavelength of light used is,
(a) 400 Å
(b) 500 Å
(c) 600 Å
Answer:
(b) 500 Å
Hint.
For diffraction minima, d sin θ = nλ
λ = \(\frac { dsin\theta }{ n } =\frac { 1\times { 10 }^{ -5 }\times { 10 }^{ -2 }\times sin30° }{ 1 } \) = 0.5 x 10-7
λ = 500 Å
![]()
Question 17.
A ray of light strikes a glass plate at an angle 60°. If the reflected and refracted rays are perpendicular to each other, the refractive index of the glass is,
(a) √3
(b) \(\frac { 3 }{ 2 }\)
(c) \(\sqrt { \frac { 3 }{ 2 } } \)
(d) 2
Answer:
(a) √3
Hint.
Angle of refraction r = 60° ; Angle of incident i = 30°
sin i =n x sin r
n = \(\frac {sin 30°}{ sin 60°} \) = √3
Question 18.
One of the of Young’s double slits is covered with a glass plate as shown in figure. The position of central maximum will,
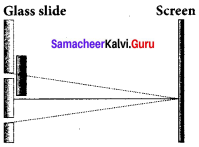
(a) get shifted downwards
(b) get shifted upwards
(c) will remain the same
(d) data insufficient to conclude
Answer:
(b) get shifted upwards
Question 19.
Light transmitted by Nicol prism is,
(a) partiallypolarised
(b) unpolarised
(c) plane polarised
(d) elliptically polarised
Answer:
(c) plane polarised
![]()
Question 20.
The transverse nature of light is shown in,
(a) interference
(b) diffraction
(c) scattering
(d) polarisation
Answer:
(d) polarisation
Samacheer Kalvi 12th Physics Optics Short Answer Questions
Question 1.
State the laws of reflection.
Answer:
(a) The incident ray, reflected ray and normal to the reflecting surface all are coplanar (ie. lie in the same plane).
(b) The angle of incidence i is equal to the angle of reflection r. i = r
Question 2.
What is angle of deviation due to reflection?
Answer:
The angle between the incident and deviated light ray is called angle of deviation of the light ray. It is written as, d= 180 – (i + r).
As, i = r in reflection, we can write angle of deviation ‘ in reflection at plane surface as, d = 180 – 2i
Question 3.
Give the characteristics of image formed by a plane mirror.
Answer:
- The image formed by a plane mirror is virtual, erect, and laterally inverted.
- The size of the image is equal to the size of the object.
- The image distance far behind the mirror is equal to the object distance in front of it.
- If an object is placed between two plane mirrors inclined at an angle 0, then the number of images n formed is as, n = \(\left( \frac { 360 }{ \theta } -1 \right) \)
Question 4.
Derive the relation between ƒ and R for a spherical mirror.
Let C be the centre of curvature of the mirror. Consider a light ray parallel to the principal axis is incident on the mirror at M and passes through the principal focus F after reflection. The geometry of reflection of the incident ray is shown in figure. The line CM is the normal to the mirror at M. Let i be the angle of incidence and the same will be the angle of reflection. If MP is the perpendicular from M on the principal axis, then from the geometry, The angles ∠MCP = i and ∠MFP = 2i From right angle triangles ∆MCP and ∆MFP,
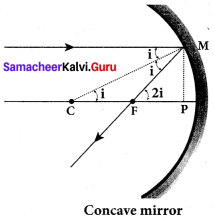
\(\frac { 1 }{ f }\) = \(\left(\frac{n_{2}}{n_{1}}-1\right)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\)
tan i = \(\frac { PM }{ PC }\) and tan 2 i = \(\frac { PM }{ PF }\)
As the angles are small, tan i ≈ i = \(\frac { PM }{ PC }\) and tan 2 i = \(\frac { PM }{ PF }\)
Simplifying further, 2 = \(\frac { PM }{ PC }\) and tan = \(\frac { PM }{ PF }\) ;2PF = PC
PF is focal length/and PC is the radius of curvature R.
2 ƒ= R (or) ƒ = \(\frac { R }{ 2 }\)
ƒ = \(\frac { R }{ 2 }\) is the relation between ƒ and R.
Question 5.
What are the Cartesian sign conventions for a spherical mirror?
Answer:
- The Incident light is taken from left to right (i.e. object on the left of mirror).
- All the distances are measured from the pole of the mirror (pole is taken as origin).
- The distances measured to the right of pole along the principal axis are taken as positive.
- The distances measured to the left of pole along the principal axis are taken as negative.
- Heights measured in the upward perpendicular direction to the principal axis are taken as positive.
- Heights measured in the downward perpendicular direction to the principal axis, are taken as negative.
![]()
Question 6.
What is optical path? Obtain the equation for optical path of a medium of thickness d and refractive index n.
Answer:
Optical path of a medium is defined as the distance d’ light travels in vacuum in the same time it travels a distance d in the medium.
Let us consider a medium of refractive index n and thickness d. Light travels with a speed v through the medium in a time t. Then we can write,
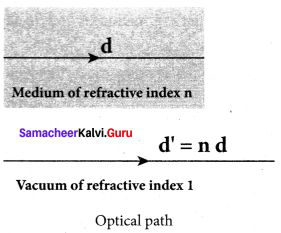
v = \(\frac { d }{ t }\); rewritten as, t = \(\frac { d }{ v }\)
In the same time, light can cover a greater distance d’
in vacuum as it travels with greater speed c in vacuum.
Then we have,
c = v = \(\frac { d’ }{ t }\); rewritten as, t = \(\frac { d’ }{ c }\)
As the time taken in both the cases is the same, we can equate the time t as,
\(\frac { d’ }{ c }\) = \(\frac { d }{ v }\)
rewritten for the optical path d’ as d’ = \(\frac { c }{ v }\)d
As, \(\frac { c }{ v }\) = n ; The optical path d’ is, d’ = nd
As n is always greater than 1, the optical path d’ of the medium is always greater than d.
Question 7.
State the laws of refraction.
Answer:
Law of refraction is called Snell’s law.
Snell’s law states that,
(a) The incident ray, refracted ray and normal to the refracting surface are all coplanar (i.e. lie in the same plane).
(b) The ratio of angle of incident i in the first medium to the angle of reflection r in the second medium is equal to the ratio of refractive index of the second medium n2 to that of the refractive index of the first medium n1.
\(\frac { sin i }{ sin r }\) = \(\frac { { n }_{ 2 } }{ { n }_{ 1 } } \).
Question 8.
What is angle of deviation due to refraction?
Answer:
The angle between the incident and deviated light is called angle of deviation. When light travels from rarer to denser medium it deviates towards normal. The angle of deviation in this case is, d = i – r
![]()
Question 9.
What is principle of reversibility?
Answer:
The principle of reversibility states that light will follow exactly the same path if its direction of travel is reversed.
Question 10.
What is relative refractive index?
Answer:
Snell’s law, the term \(\left( \frac { { n }_{ 2 } }{ { n }_{ 1 } } \right) \) is called relative refractive index of second medium with respect to the first medium which is denoted as (n21). n21 = \(\frac { { n }_{ 2 } }{ { n }_{ 1 } } \)
Question 11.
Obtain the equation for apparent depth.
Answer:
Light from the object O at the bottom of the tank passes from denser medium (water) to rarer medium (air) to reach our eyes. It deviates away from the normal in the rarer medium at the point of incidence B. The refractive index of the denser medium is n1 and rarer medium is n2. Here, n1 > n2. The angle of incidence in the denser medium is i and the angle of refraction in the rarer medium is r. The lines NN’ and OD are parallel. Thus angle ∠DIB is also r. The angles i and r are very small as the diverging light from O entering the eye is very narrow. The Snell’s law in product form for this refraction is,
n1 sin i = n2 sin r
As the angles i and r are small, we can approximate, sin i ≈ tan i;
n1 tan i = n2 tan i
In triangles ∆DOB and ∆DIB,
tan(i) = \(\frac { DB }{ DO }\) and tan(r) = \(\frac { DB }{ DI }\)
n1 = \(\frac { DB }{ DO }\) n2 = \(\frac { DB }{ DI }\)
DB is cancelled on both sides, DO is the actual depth d and DI is the apparent depth d’.
Rearranging the above equation for the apparent depth d’,
d’ = \(\left( \frac { { n }_{ 2 } }{ { n }_{ 1 } } \right) \)d
As the rarer medium is air and its refractive index n2 can be taken as 1, (n2 = 1). And the refractive index n1 of denser medium could then be taken as n, (n1 = n).
In that case, the equation for apparent depth becomes,
d = \(\frac { d }{ n }\)
Question 12.
Why do stars twinkle?
Answer:
The stars actually do not twinkle. They appear twinkling because of the movement of the atmospheric layers with varying refractive indices which is clearly seen in the night sky.
Question 13.
What is critical angle and total internal reflection?
Answer:
The angle of incidence in the denser medium for which the refracted ray graces the boundary is called critical angle ic.
The entire light is reflected back into the denser medium itself. This phenomenon is called total internal reflection.
Question 14.
Obtain the equation for critical angle.
Answer:
Snell’s law in the product form, equation for critical angle incidence becomes,
n1 sini ic = n2 sin 90°
n1 sini ic = n2 (∵ sin 90° = 1)
sini ic = \(\left( \frac { { n }_{ 2 } }{ { n }_{ 1 } } \right) \)
Here, n1 > n2
If the rarer medium is air, then its refractive index is 1 and can be taken as n itself, i.e. (n2 = 1) and (n1= n).
sini ic = \(\frac { 1 }{ n }\) (or) ic = sin-1 \(\left( \frac { 1 }{ n } \right) \)
Question 15.
Explain the reason for glittering of diamond.
Answer:
Diamond appears dazzling because the total internal reflection of light happens inside the diamond. The refractive index of only diamond is about 2.417. It is much larger than that for ordinary glass which is about only 1.5. The critical angle of diamond is about 24.4°. It is much less than that of glass. A skilled diamond cutter makes use of this larger range of angle of incidence (24.4° to 90° inside the diamond), to ensure that light entering the diamond is total internally reflected from the many cut faces before getting out. This gives a sparkling effect for diamond.
![]()
Question 16.
What are mirage and looming?
Answer:
Mirage: Mirage takes place in hot regions. The light from distant objects appears to be reflected from ground. For mirage to form refractive index goes on increasing as we go up. Looming: Looming takes place in cold regions. The light from distant objects appears to be flying. For looming to form refractive index goes on decreasing.
Question 17.
Write a short notes on the prisms making use of total internal reflection.
Answer:
Prisms can be designed to reflect light by 90° or by 180° by making use of total internal reflection. The critical angle ic for the material of the prism must be less than 45°. This is true for both crown glass and flint glass. Prisms are also used to invert images without changing their size.
Question 18.
What is Snell’s window?
Answer:
When light entering the water from outside is seen from inside the water, the view is restricted to a particular angle equal to the critical angle ic. The restricted illuminated circular area is called Snell’s window.
Question 19.
Write a note on optical fibre.
Answer:
Transmitting signals through optical fibres is possible due to the phenomenon of total internal reflection. Optical fibres consists of inner part called core and outer part called cladding (or) sleeving. The refractive index of the material of the core must be higher than that of the cladding for total internal reflection to happen. Signal in the form of light is made to incident inside the core-cladding boundary at an angle greater than the critical angle. Hence, it undergoes repeated total internal reflections along the length of the fibre without undergoing any refraction.
Question 20.
Explain the working of an endoscope.
Answer:
An endoscope is an instrument used by doctors which has a bundle of optical fibres that are used to see inside a patient’s body. Endoscopes work on the phenomenon of total internal reflection. The optical fibres are inserted in to the body through mouth, nose or a special hole made in the body. Even operations could be carried out with the endoscope cable which has the necessary instruments attached at their ends.
![]()
Question 21.
What are primary focus and secondary focus of convex lens?
Answer:
Primary focus: The primary focus F1 is defined as a point where an object should be placed to give parallel emergent rays to the principal axis.
Secondary focus: The secondary focus F2 is defined as a point where all the parallel rays travelling close to the principal axis converge to form an image on the principal axis.
Question 22.
What are the sign conventions followed for lenses?
Answer:
The sign conventions for thin lenses differ only in the signs followed for focal lengths.
(a) The sign of focal length is not decided on the direction of measurement of the focal length from the pole of the lens as they have two focal lengths, one to the left and another to the right (primary and secondary focal lengths on either side of the lens).
(b) The focal length of the thin lens is taken as positive for a converging lens and negative for a diverging lens.
Question 23.
Arrive at lens equation from lens maker’s formula.
Answer:
From refraction through a double convex lens, the relation between the object distance u, image distance v1 and radius of curvature R1 as
\(\frac { { \mu }_{ 2 } }{ { v }_{ 1 } } -\frac { { \mu }_{ 1 } }{ u } =\frac { { \mu }_{ 2 }-{ \mu }_{ 1 } }{ { R }_{ 1 } } \) …… (1)
The relation between the object distance image distance v1 and radius of curvature R2 can be
\(\frac { { \mu }_{ 1 } }{ { v } } -\frac { { { \mu }_{ 2 } } }{ v_{ 1 } } =\frac { { \mu }_{ 1 }-{ \mu }_{ 2 } }{ { R }_{ 2 } } \) …… (2)
Adding equation (1) and (2)

If the object is placed at infinity (µ = ∞), the image will be formed at the focus. i.e.v = ƒ

This is len’s maker’s formula. When the lens is placed in air µ1 = 1 and µ2 = µ.
Equation (4) becomes,

From equation (3) and (4), we have \(\frac { 1 }{ v }\)–\(\frac { 1 }{ u }\)
=\(\frac { 1 }{ ƒ }\)
This is the len’s equation.
Question 24.
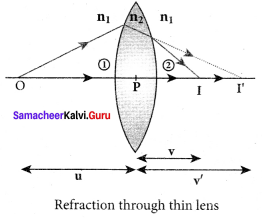
Obtain the equation for lateral magnification for thin lens.
Answer:
Lateral magnification in terms of u and ƒ.
The thin lens formula is
\(\frac { 1 }{ v }\)–\(\frac { 1 }{ u }\)=\(\frac { 1 }{ ƒ }\)
Multiplying on both sides by ‘u’
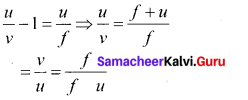
In terms of v and ƒ multiplying by v, we get
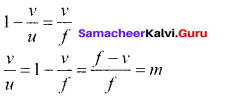
Hence, lateral magnification for thin lens,
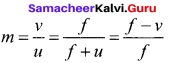
Question 25.
What is power of a lens?
Answer:
The power of a lens P is defined as the reciprocal of its focal length.
p = \(\frac { 1 }{ ƒ }\)
The unit of power is diopter D.
![]()
Question 26.
Derive the equation for effective focal length for lenses in contact.
Answer:
Consider a two thin lenses in contact. In the absence of second lens L2, the first lens L1 will form a real image I’. Using thin lens formula.
\(\frac { 1 }{ { f }_{ 2 } } \)=\(\frac { 1 }{ v’ }\)–\(\frac { 1 }{ u }\) ….. (1)
The image I’ acts as a virtual object (u = v’) for the second lens L2 which finally forms its real image I at distance v. Thus
\(\frac { 1 }{ { f }_{ 2 } } \)=\(\frac { 1 }{ v }\)–\(\frac { 1 }{ v’ }\) ….. (2)
Adding equation (1) and (2) we get,
\(\frac { 1 }{ { f }_{ 1 } } \)+\(\frac { 1 }{ { f }_{ 2 } } \)=\(\frac { 1 }{ v }\)–\(\frac { 1 }{ u }\) ….. (3)
For the combination of thin lenses in contact, if ‘f’ is the equivalent focal length, then
\(\frac { 1 }{ v }\)–\(\frac { 1 }{ u }\)=\(\frac { 1 }{ ƒ }\) ….. (4)
From equations (3) and (4), the effective focal length for lenses in contact.
\(\frac { 1 }{ ƒ }\)=\(\frac { 1 }{ { f }_{ 1 } } \)+\(\frac { 1 }{ { f }_{ 2 } } \)
Question 27.
What is angle of minimum deviation?
Answer:
The minimum value of the angle of deviation suffered by a ray on passing through a prism is called the angle of minimum deviation.
Question 28.
What is dispersion?
Answer:
The phenomenon of spliting of white light into its component colours on passing through a refracting medium is called dispersion.
Question 29.
How are rainbows formed?
Answer:
Rainbow is formed by dispersion of sunlight into its constituent colours by raindrops which disperse sunlight by refraction and deviate the colours by total internal reflection.
Question 30.
What is Rayleigh’s scattering?
Answer:
The scattering of light by particles in a medium without a change in wavelength is called as Rayleigh’s scattering.
![]()
Question 31.
Why does sky appear blue?
Answer:
Blue colour of the sky is due to scattering of sunlight by air molecules. According to Rayleigh’s law, intensity of scattered light, I ∝ \(\frac { 1 }{ { \lambda }^{ 4 } } \) So blue light of shorter wavelength is scattered much more than red light of larger wavelength. The blue component is proportionally more in light coming from different parts of the sky. That is why the sky appears blue.
Question 32.
What is the reason for reddish appearance of sky during sunset and sunrise?
Answer:
During sunrise or sunset, the sun is near the horizon. Sunlight has to travel a greater distance. So shorter waves of blue region are scattered away by the atmosphere. Red waves of longer wavelength are least scattered and reach the observer. So the sun appears red.
Question 33.
Why do clouds appear white?
Answer:
Clouds have large particles like dust and water droplets which scatter light of all colours almost equally. Hence clouds generally appear white.
Question 34.
What are the salient features of corpuscular theory of light?
Answer:
- According this theory, light is emitted as tiny, massless (negligibly small mass) and perfectly elastic particles called corpuscles.
- As the corpuscles are very small, the source of light does not suffer appreciable loss of mass even if it emits light for a long time.
- On account of high speed, they are unaffected by the force of gravity and their path is a straight line in a medium of uniform refractive index.
- The energy of light is the kinetic energy of these corpuscles. When these corpuscles impinge on the retina of the eye, the vision is produced.
- The different size of the corpuscles is the reason for different colours of light.
- When the corpuscles approach a surface between two media, they are either attracted or repelled.
- The reflection of light is due to the repulsion of the corpuscles by the medium and refraction of light is due to the attraction of the corpuscles by the medium.
Question 35.
What is wave theory of light?
Answer:
Light is a disturbance from a source that travels as longitudinal mechanical waves through the either medium that was presumed to pervade all space as mechanical wave requires medium for its propagation. The wave theory could successfully explain phenomena of reflection, refraction, interference and diffraction of light.
![]()
Question 36.
What is electromagnetic wave theory of light?
Answer:
Electromagnetic wave theory:
Maxwell (1864) proved that light is an electromagnetic wave which is transverse in nature carrying electromagnetic energy. He could also show that no medium is necessary for the propagation of electromagnetic waves. All the phenomenon of light could be successfully explained by this theory.
Question 37.
Write a short note on quantum theory of light.
Answer:
Albert Einstein (1905), endorsing the views of Max Plank (1900), was able to explain photoelectric effect in which light interacts with matter as photons to eject the electrons. A photon is a discrete packet of energy. Each photon has energy E of,
E = hv
Where, h is Plank’s constant (h = 6.625 x 10-34J s) and v is frequency of electromagnetic wave. As light has both wave as well as particle nature it is said to have dual nature. Thus, it is concluded that light propagates as a wave and interacts with matter as a particle.
Question 38.
What is a wave front?
Answer:
A wavefront is the locus of points which are in the same state or phase of vibration.
Question 39.
What is Huygens’ principle?
Answer:
According to Huygens principle, each point of the wavefront is the source of secondary wavelets emanating from these points spreading out in all directions with the speed of the wave. These are called as secondary wavelets.
Question 40.
What is interference of light?
Answer:
The phenomenon of addition or superposition of two light waves which produces increase in intensity at some points and decrease in intensity at some other points is called interference of light.
![]()
Question 41.
What is phase of a wave?
Answer:
Phase is a particular point in time on the cycle of a waveform, measured as an angle in degrees.
Question 42.
Obtain the relation between phase difference and path difference.
Answer:
Phase difference (Φ):
It is the difference expressed in degrees or radians between two waves having same frequency and referenced to same point in time.
Path difference (δ):
It is the difference between the lengths of two paths of the two different having same frequency and travelling at same velocity. δ =\(\frac { \lambda }{ 2\pi } \) Φ
Question 43.
What are coherent sources?
Answer:
Two light sources are said to be coherent if they produce waves which have same phase or constant phase difference, same frequency or wavelength (monochromatic), same waveform and preferably same amplitude.
Question 44.
What is intensity division?
Answer:
Intensity’ or amplitude division: If we allow light to pass through a partially silvered mirror (beam splitter), both reflection and refraction take place simultaneously. As the two light beams are obtained from the same light source, the two divided light beams will be coherent beams. They will be either in-phase or at constant phase difference.
Question 45.
How does wavefront division provide coherent sources?
Answer:
Wavefront division is the most commonly used method for producing two coherent sources. A point source produces spherical wavefronts. All the points on the wavefront are at the same phase. If two points are chosen on the wavefront by using a double slit, the two points will act as coherent sources.
![]()
Question 46.
How do source and images behave as coherent sources?
Answer:
Source and images: In this method a source and its image will act as a set of coherent source, because the source and its image will have waves in-phase or constant phase difference. The Instrument, Fresnel’s biprism uses two virtual sources as two coherent sources and the instrument, Lloyd’s mirror uses a source and its virtual image as two coherent sources.
Question 47.
What is bandwidth of interference pattern?
Answer:
The bandwidth (β) is defined as the distance between any two consecutive bright or dark fringes.
Question 48.
What is diffraction?
Answer:
Diffraction is bending of waves around sharp edges into the geometrically shadowed region.
Question 49.
Differentiate between Fresnel and Fraunhofer diffraction.
Answer:
| S.No. | Fresnel diffraction | Fraunhofer diffraction |
| 1. | Spherical or cylindrical wavefront undergoes diffraction | Plane wavefront undergoes diffraction |
| 2. | Light wave is from a source at finite distance | Light wave is from a source at infinity |
| 3. | For laboratory conditions, convex lenses need not be used | In laboratory conditions, convex lenses are to be used |
| 4. | difficult to observe and analyse | Easy to observe and analyse |
Question 50.
Discuss the special cases on first minimum in Fraunhofer diffraction.
Let us consider the condition for first minimum with (n = 1). a sin θ = λ
The first minimum has an angular spread of, sin θ = \(\frac { \lambda }{ a } \). Special cases to discuss on the condition.
1. When a < λ, the diffraction is not possible, because sin 0 can never be greater than 1.
2. When a ≥ λ, the diffraction is possible.
- For a = λ, sin θ = 1 i.e, θ = 90°. That means the first minimum is at 90°. Hence, the central maximum spreads fully in to the geometrically shadowed region leading to bending of the diffracted light to 90°.
- For a >> λ, sin θ << 1 i.e, the first minimum will fall within the width of the slit itself. The diffraction will not be noticed at all.
3. When a > λ and also comparable, say a = 2λ, sin θ = \(\frac { \lambda }{ a } \) = \(\frac { \lambda }{ { 2\lambda } } \) =\(\frac { 1 }{ 2 }\); then θ = 30°. These are practical cases where diffraction could be observed effectively.
![]()
Question 51.
What is Fresnel’s distance? Obtain the equation for Fresnel’s distance.
Answer:
Fresnel’s distance is the distance up to which the ray optics is valid in terms of rectilinear propagation of light.
Fresnel’s distance z as, z = \(\frac { { a }^{ 2 } }{ 2\lambda } \).
Question 52.
Mention the differences between interference and diffraction.
Answer:
| S.No. | Interference | Diffraction |
| 1. | Superposition of two waves | Bending of waves around edges |
| 2. | Superposition of waves from two coherent sources. | Superposition wavefronts emitted from various points of the same wavefront. |
| 3. | Equally spaced fringes. | Unequally spaced fringes |
| 4. | Intensity of all the bright fringes is almost same | Intensity falls rapidly for higher orders |
| 5. | Large number of fringes are obtained | Less number of fringes are obtained |
Question 53.
What is a diffraction grating?
Answer:
A diffraction grating is an optical component with a periodic structure that splits and diffracts light into several beams travelling in different directions.
Question 54.
What are resolution and resolving power?
Answer:
Optical resolution describes the ability of an imaging system to resolve detail in the object that is being imaged. Resolving power is the ability of an optical instrument to resolve or separate the image of two nearby point objects so that they can be distinctly seen. It is equal to the reciprocal of the limit of resolution of the optical instrument.
Question 55.
What is Rayleigh’s criterion?
Answer:
The images of two point objects are just resolved when the central maximum of the diffraction pattern of one falls over the first minimum of the diffraction pattern of the other.
![]()
Question 56.
What is polarisation?
Answer:
The phenomenon of restricting the vibrations of light (electric or magnetic field vector) to a particular direction perpendicular to the direction of wave propagation motion is called polarization of light.
Question 57.
Differentiate between polarised and unpolarised light.
Answer:
| S.No. | Polarised light | Unpolarised light |
| 1. | Consists of waves having their electric field vibrations in a single plane normal to the direction of ray. | Consists of waves having their electric field vibrations equally distributed in all directions normal to the direction of ray. |
| 2. | Asymmetrical about the ray direction | Symmetrical about the ray direction |
| 3. | It is obtained from unpolarised light with the help of polarisers | Produced by conventional light sources. |
Question 58.
Discuss polarisation by selective absorption.
Answer:
Selective absorption is the property of a material which transmits w’aves whose electric fields vibrate in a plane parallel to a certain direction of orientation and absorbs all other waves. The polaroids or polarisers are thin commercial sheets which make use of the property of selective absorption to produce an intense beam of plane polarised light. Selective absorption is also called as dichroism.
Question 59.
What are polariser and analyser?
Answer:
Polariser:
The Polaroid which plane polarises the unpolarised light passing through it is called a polariser.
Analyser:
The polaroid which is used to examine whether a beam of light is polarised or not is called an analyser.
Question 60.
What are plane polarised, unpolarised and partially polarised light?
Answer:
Plane polarised:
If the vibrations of a wave are present in only one direction in a plane perpendicular to the direction of propagation of the wave is said to be polarised or plane polarised light.
Unpolarised:
A transverse wave which has vibrations in all directions in a plane perpendicular to the direction of propagation is said to be unpolarised light.
Partially polarised light:
If the intensity of light varies between maximum and minimum for every’ rotation of 90° of the analyser, the light is said to be partially polarised light.
![]()
Question 61.
State and obtain Malus’ law.
Answer:
When a beam of plane polarised light of intensity I0 is incident on an analyser, the light transmitted of intensity I from the analyser varies directly as the square of the cosine of the angle 0 between the transmission axis of polariser and analyser. This is known as Malus’ law. I = I0 cos2θ
Question 62.
List the uses of polaroids.
Answer:
Uses of polaroids:
- Polaroids are used in goggles and cameras to avoid glare of light.
- Polaroids are useful in three dimensional motion pictures i.e., in holography.
- Polaroids are used to improve contrast in old oil paintings.
- Polaroids are used in optical stress analysis.
- Polaroids are used as window glasses to control the intensity of incoming light.
Question 63.
State Brewster’s law.
Answer:
The law states that the tangent of the polarising angle for a transparent medium is equal to its refractive index, tan i = n. This relation is known as Brewster’s law.
Question 64.
What is angle of polarisation and obtain the equation for angle of polarisation.
Answer:
The angle of incidence at which a beam of unpolarised light falling on a transparent surface is reflected as a beam of plane polarised light is called polarising angle or Brewster’s angle. It is denoted by ip
ip = 90° – Rp
Question 65.
Discuss about pile of plates.
Answer:
The phenomenon of polarisation by reflection is used in the construction of pile of plates. It consists of a number of glass plates placed one over the other. The plates are inclined at an angle of 33.7° (90° – 56.3°) to the axis of the tube. A beam of unpolarised light is allowed to fall on the pile of plates along the axis of the tube. So, the angle of incidence of light will be at 56.3° which is the polarising angle for glass.
The vibrations perpendicular to the plane of incidence are reflected at each surface and those parallel to it are transmitted. The larger the number of surfaces, the greater is the intensity of the reflected plane polarised light. The pile of plates is used as a polarizer and also as an analyser.
![]()
Question 66.
What is double refraction?
Answer:
When a ray of unpolarised light is incident on a calcite crystal, two refracted rays are produced. Hence, two images of a single object are formed. This phenomenon is called double refraction.
Question 67.
Mention the types of optically active crystals with example.
Answer:
Types of optically active crystals:
Uniaxial crystals:
Crystals like calcite, quartz, tourmaline and ice having only one optic axis are called uniaxial crystals.
Biaxial crystals:
Crystals like mica, topaz, selenite and aragonite having two optic axes are called biaxial crystals.
Question 68.
Discuss about Nicol prism.
Answer:
Nicol prism is an optical device incorporated in optical instruments both for producing and analysing plane polarised light. The construction of a Nicol prism is based on the phenomenon of Double refraction. One of the most common forms of the Nicol prism is made by taking a calcite crystal which is a double refracting crystal with its length three times its breadth.
It is cut into two halves along the diagonal so that their face angles are 72° and 108°. The two halves are joined i together by a layer of Canada balsam, a transparent cement.
Question 69.
How is polarisation of light obtained by scattering of light?
Answer:
The light from a clear blue portion of the sky shows a rise and fall of intensity when viewed through a polaroid which is rotated. This is because of sunlight, which has changed its I direction (having been scattered) on encountering the molecules of the earth’s atmosphere. The electric field of light interact with the electrons present in the air molecules.
Under the influence of the electric field of the incident wave the electrons in the molecules acquire components of motion in both these directions. We have an observer looking at 90° to the direction of the sun. Clearly, charges accelerating parallel do not radiate energy towards this observer since their acceleration has no transverse component. The radiation scattered by the molecule is therefore polarized perpendicular to the plane.
Question 70.
Discuss about simple microscope and obtain the equations for magnification for near point focusing and normal focusing.
Answer:
A simple microscope is a single magnifying (converging) lens of small focal length. The idea is to get an erect, magnified and virtual image of the object. For this the object is placed between F and P on one side of the lens and viewed from other side of the lens. There are two magnifications to be discussed for two kinds of focusing.
- Magnification in near point focusing m = 1 + \(\frac { D }{ f }\)
- Magnification in normal focusing (angular magnification), m = \(\frac { D }{ f }\)
![]()
Question 71.
What are near point and normal focusing?
Answer:
- Near point focusing:
The image is formed at near point, i.e. 25 cm for normal eye. This distance is also called as least distance D of distinct vision. In this position, the eye feels comfortable but there is little strain on the eye. - Normal focusing:
The image is formed at infinity. In this position the eye is most relaxed to view the image.
Question 72.
Why is oil immersed objective preferred in a microscope?
Answer:
It is best to use an oil-immersed objective at high magnification as the oil compensates for short focal lengths associated with larger magnifications.
Question 73.
What are the advantages and disadvantages of using a reflecting telescope?
Answer:
Advantages:
- The main advantage is reflector telescope can escape from chromatic aberration because wavelength does not effect reflection.
- The primary mirror is very stable because it is located at the back of the telescope and can be support in the back.
- More cost effective than refractor of similar size.
- Easier to make a high quality mirror than lens because mirror need to only concern with one side of the curvature.
Disadvantages:
- Optical misalignment can occur quite easily.
- Require frequent cleaning because the inside is expose to the atmosphere.
- Secondary mirror can cause diffraction of original incoming light rays causing the “Christmas star effect” where a bright object have spikes.
Question 74.
What is the use of an erecting lens in a terrestrial telescope?
Answer:
A terrestrial telescope has an additional erecting lens to make the final image erect.
Question 75.
What is the use of collimator?
Answer:
The collimator is an arrangement to produce a parallel beam of light.
![]()
Question 76.
What are the uses of spectrometer?
Answer:
The spectrometer is an optical instrument used to study the spectra of different sources of light and to measure the refractive indices of materials.
Question 77.
What is myopia? What is its remedy?
Answer:
Myopia (or) short sightedness:
It is a vision defect in which a person can see nearby objects clearly but cannot see the distant objects clearly beyond a certain point.
Remedy (correction):
A myopia eye is corrected by using a concave lens of focal length equal to the distance of the far point F from the eye.
Question 78.
What is hypermetropia? What is its remedy?
Answer:
Hypermetropia (or) Long sightedness: It is a vision defect in which a person can see the distant objects clearly but cannot see the nearby objects clearly.
Remedy (correction): A hypermetropic eye is corrected by using a convex lens of suitable focal length.
Question 79.
What is presbyopia?
Answer:
This defect is similar to hypermetropia i.e., a person having this defect cannot see nearby objects distinctly, but can see distant objects without any difficulty. This defect occurs in elderly persons (aged persons).
Question 80.
What is astigmatism?
Answer:
Astigmatism is the defect arising due to different curvatures along different planes in the eye lens. Astigmatic person cannot see all the directions equally well. The defect due to astigmatism is more serious than myopia and hyperopia.
![]()
Samacheer Kalvi 12th Physics Optics Long Answer Questions
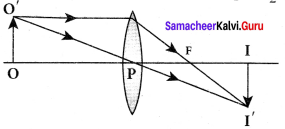
Question 1.
Derive the mirror equation and the equation for lateral magnification.
Answer:
The mirror equation:
1. The mirror equation establishes a relation among object distance u, image distance v and focal length/for a spherical mirror. An object AB is considered on the principal axis of a concave mirror beyond the center of curvature C’.
2. Let us consider three paraxial rays from point B on the object.
3. The first paraxial ray BD travelling parallel to principal axis is incident on the concave mirror at D, close to the pole P. After reflection the ray passes through the focus F. The second paraxial ray BP incident at the pole P is reflected along PBThe third paraxial ray BC passing through centre of curvature C, falls normally on the mirror at E is reflected back along the same path.
4. The three reflected rays intersect at the point B’. A perpendicular drawn as A’ B’ to the principal axis is the real, inverted image of the object AB.
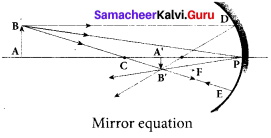
As per law of reflection, the angle of incidence ∠BPA is equal to the angle of reflection ∠B’PA’. The triangles ∆BPA and ∆B’PA’ are similar. Thus, from the rule of similar triangles,
\(\frac { A’B’ }{ AB }\) = \(\frac { PA’ }{ PA }\) …….. (1)
The other set of similar triangles are, ADPF and A BA.’ F. (PD is almost a straight vertical line)
\(\frac { A’B’ }{ PD }\) = \(\frac { AF’ }{ PF }\)
As, the distances PD = AB the above equation becomes,
\(\frac { A’B’ }{ AB }\) = \(\frac { AF’ }{ PF }\) ……… (2)
From equations (1) and (2) we can write,
\(\frac { PA’ }{ PA }\) = \(\frac { AF’ }{ PF }\)
As, A’ F = PA’ – PF, the above equation becomes,
\(\frac {PA’ }{ PA }\) = \(\frac { PA’-PF’P }{ PF }\) ……….. (3)
We can apply the sign conventions for the various distances in the above equation.
PA = – u, PA’ = -v, PF = -f
All the three distances are negative as per sign convention, because they are measured to the left of the pole. Now, the equation (3) becomes,
\(\frac { -v }{ -u }\) = \(\frac { -v\left( -f \right) }{ -f } \)
On further simplification,
\(\frac { -v }{ -u }\) = \(\frac { v-f }{ f }\); \(\frac { v }{ u }\)=\(\frac { v }{ f }\)=1
Dividing either side with v,
\(\frac { 1 }{ u }\)=\(\frac { 1 }{ f }\)=\(\frac { 1 }{ v }\)
After rearranging,
\(\frac { 1 }{ v }\)+\(\frac { 1 }{ u }\)=\(\frac { 1 }{ f }\) ……… (4)
The above equation (4) is called mirror equation.
Lateral magnification in spherical mirrors:
The lateral or transverse magnification is defined as the ratio of the height of the image to the height of the object. The height of the object and image are measured perpendicular to the principal axis.
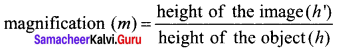
m=\(\frac { h’ }{ h }\) ……..(5)
Applying proper sign conventions for equation (1),
\(\frac { A’B’ }{ AB }\) = \(\frac { PA’ }{ PA }\)
A’B’ = -h, AB = h, PA’ = -v, PA = -u
\(\frac { -h’ }{ h }\)=\(\frac { -v }{ -u }\)
On simplifying we get,
m=\(\frac { h’ }{ h }\)=-\(\frac { v }{ u }\) ………. (6)
Using mirror equation, we can further write the magnification as,
m=\(\frac { h’ }{ h }\)–\(\frac { f-v }{ f }\)=\(\frac { f }{ f-u }\) ………… (7)
Question 2.
Describe the Fizeau’s method to determine speed of light.
Answer:
Fizeau’s method to determine speed of light:
Apparatus:
The light from the source S was first allowed to fall on a partially silvered glass plate G kept at an angle of 45° to the incident light from the source. The light then was allowed to pass through a rotating toothed-wheel with N teeth and N cuts of equal widths whose speed of rotation could be varied through an external mechanism. The light passing through one cut in the wheel will get reflected by a mirror M kept at a long distance d, about 8 km from the toothed w’heel. If the toothed wheel was not rotating, the reflected light from the mirror would again pass through the same cut and reach the eyes of the observer through the partially silvered glass plate.
Working:
The angular speed of rotation of the toothed wheel was increased from zero to a value to until light passing through one cut would completely be blocked by the adjacent tooth. This is ensured by the disappearance of light while looking through the partially silvered glass plate.
Expression for speed of light:
The speed of light in air v is equal to the ratio of the distance the light travelled from the toothed wheel to the mirror and back 2d to the time taken t.
v = \(\frac { 2d }{ t }\) c ….. (1)
The distance d is a known value from the arrangement. The time taken t for the light to travel the distance to and fro is calculated from the angular speed co of the toothed wheel.
The angular speed ω of the toothed wheel when the light disappeared for the first time is,
ω = \(\frac { θ }{ t }\) ……. (2)
Here, 0 is the angle between the tooth and the slot which is rotated by the toothed wheel within that time t.
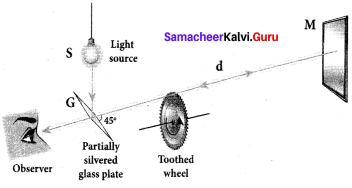

θ = \(\frac { 2π }{ 2N }\) = \(\frac { π }{ N }\)
Substituting for 0 in the equation (2) for ,
ω = \(\frac { \pi /n }{ 2 } \) = \(\frac { π }{ Nt }\)
Rewriting the above equation for t,
t = \(\frac { π }{ Nω }\) ……. (3)
Substituting t from equation (3) in equation (1), v = \(\frac { 2d }{ \pi /N\omega } \)
After rearranging,
v = \(\frac { 2dNω }{ π }\) …….. (4)
Fizeau had some difficulty to visually estimate the minimum intensity of the light when blocked by the adjacent tooth, and his value for speed of light was very close to the actual value.
![]()
Question 3.
Obtain the equation for radius of illumination (or) Snell’s window.
Answer:
The radius of Snell’s window can be deduced with the illustration as shown in figure. Light is seen from a point A at a depth d. The Snell’s law in product form, equation n2 sin i = n2 sin r for the refraction happening at the point B on the boundary between the two media is,
n1 sin ic = n2 sin 90° ……. (1)
n1 sin ic= n2 ∵ sin 90° = 1
sin ic = \(\frac { { n }_{ 2 } }{ { n }_{ 1 } } \) …….. (2)
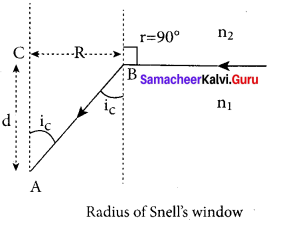
From the right angle triangle ∆ABC,
sin ic = \(\frac { R }{ \sqrt { { d }^{ 2 }+{ R }^{ 2 } } } \) ……. (3)
Equating the above two equation (3) and equation (2).
\(\frac { R }{ \sqrt { { d }^{ 2 }+{ R }^{ 2 } } } \) = \(\frac { { n }_{ 2 } }{ { n }_{ 1 } } \)


If the rarer medium outside is air, then, n2 = 1, and we can take n1 = n
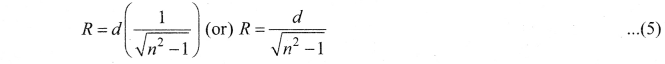
Question 4.
Derive the equation for acceptance angle and numerical aperture, of optical fiber. Acceptance angle in optical fibre:
Answer:
To ensure the critical angle incidence in the core-cladding boundary inside the optical fibre, the light should be incident at a certain angle at the end of the optical fiber while entering in to it. This angle is called acceptance angle. It depends on the refractive indices of the core n1, cladding n2 and the outer medium n3. Assume the light is incident at an angle called acceptance angle i at the outer medium and core boundary at A.
The Snell’s law in the product form, equation for this refraction at the point A.
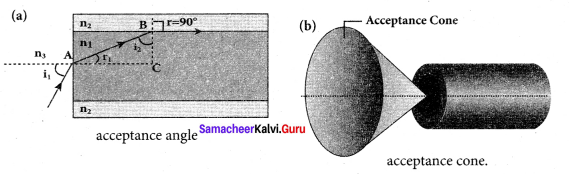
n3 sin ia = n1 sin ra …(1)
To have the total internal reflection inside optical fibre, the angle of incidence at the core-cladding interface at B should be atleast critical angle ic. Snell’s law in the product form, equation for the refraction at point B is,
n1 sin ic = n2 sin 90° …(2)
n1 sin ic= n2 ∵ sin 90° =1
∴sin ic= \(\frac { { n }_{ 2 } }{ { n }_{ 1 } } \) …(3)
From the right angle triangle ∆ABC,
ic = 90°-ra
Now, equation (3) becomes, sin (90° – ra) = \(\frac { { n }_{ 2 } }{ { n }_{ 1 } } \)
Using trigonometry’, cos ra = ra = \(\frac { { n }_{ 2 } }{ { n }_{ 1 } } \) …….. (4)
sin ra = \(\sqrt { 1-{ cos }^{ 2 }{ r }_{ a } } \)
Substituting for cos ra

If outer medium is air, then n3 = 1. The acceptance angle ia becomes,
ra=sin-1\(\left( \sqrt { { n }_{ 1 }^{ 2 }-{ n }_{ 2 }^{ 2 } } \right) \) …….. (9)
Light can have any angle of incidence from 0 to ia with the normal at the end of the optical fibre forming a conical shape called acceptance cone. In the equation (6), the term (n3 sin ia) is called numerical aperture NA of the optical fibre.
NA =n3 sin ia \(\left( \sqrt { { n }_{ 1 }^{ 2 }-{ n }_{ 2 }^{ 2 } } \right) \) …….. (10)
If outer medium is air, then n3 = 1. The numerical aperture NA becomes,
NA = sin ia = \(\left( \sqrt { { n }_{ 1 }^{ 2 }-{ n }_{ 2 }^{ 2 } } \right) \) …….. (11)
Question 5.
Obtain the equation for lateral displacement of light passing through a glass slab.
Answer:
Consider a glass slab of thickness t and refractive index n is kept in air medium. The path of the light is ABCD and the refractions occur at two points B and C in the glass slab. The angles of incidence i and refraction r are measured with respect to the normal N1and N2 at the two points B and C respectively. The lateral displacement L is the perpendicular distance CE drawn between the path of light and the undeviated path of light at point C. In the right angle triangle ∆BCE,
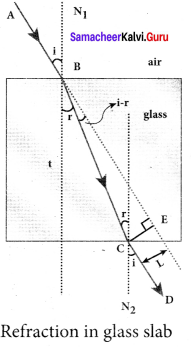
sin(i – r) = \(\frac { L }{ BC }\); BC= \(\frac { L }{ sin(i-r) } \) …… (1)
In the right angle triangle ∆BCF,
cos(r) = \(\frac { t }{ BC }\) ; BC= \(\frac { t }{ cos(r) } \) …… (2)
Equating equations (1) and (2)
\(\frac { L }{ sin(i-r) } \) = \(\frac { t }{ cos(r) } \)
After rearranging,
L = t\(\left( \frac { sin(i-r) }{ cos(r) } \right) \)
Lateral displacement depends upon the thickness of the slab. Thicker the slab, greater will be the lateral displacement. Greater the angle of incident, larger will be the lateral displacement.
![]()
Question 6.
Derive the equation for refraction at single spherical surface.
Answer:
Equation for refraction at single spherical surface:
Let us consider two transparent media having refractive indices n1and n2 are separated by a spherical surface. Let C be the centre of curvature of the spherical surface. Let a point object O be in the medium n1. The line OC cuts the spherical surface at the pole P of the surface. As the rays considered are paraxial rays, the perpendicular dropped for the point of incidence to the principal axis is very close to the pole or passes through the pole itself.
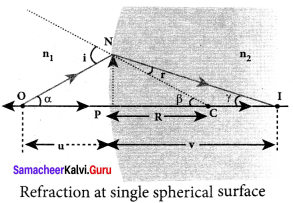
Light from O falls on the refracting surface at N. The normal drawn at the point of incidence passes through the centre of curvature C. As n2 > n1, light in the denser medium deviates towards the normal and meets the principal axis at I where the image is formed.
Snell’s law in product form for the refraction at the point N could be written as,
n1 sin i = n2 sin r …(1)
As the angles are small, sin of the angle could be approximated to the angle itself.
n1 i = n2 r …(2)
Let the angles,
∠NOP = α, ∠NCP = β, ∠NIP = γ
tan α = \(\frac { PN }{ PO }\);tan β = \(\frac { PN }{ PC }\);tan γ = \(\frac { PN }{ PI }\)
As these angles are small, tan of the angle could be approximated to the angle itself.
α = \(\frac { PN }{ PO }\); β = \(\frac { PN }{ PC }\); γ = \(\frac { PN }{ PI }\) …….. (3)
For the triangle, ∆ONC,
I = α + β …….. (4)
For the triangle, ∆INC,
β = r + γ (or) r = β – γ ……… (5)
Substituting for I and r from equations (4) and (5) in the equation (2).
n1 (α + β) = n2 (β – γ)
Rearranging,
n1 α + n2γ = (n2 – n1)β
Substituting for α, β and γ from equation (3)
n1 = (\(\frac { PN }{ PO }\)) + n2 = (\(\frac { PN }{ PI }\)) = (n2-n1) (\(\frac { PN }{ PC }\))
Further simplifying by cancelling PN,
\(\frac { { n }_{ 1 } }{ PO } \) + \(\frac { { n }_{ 2 } }{ PI } \) = \(\frac { { n }_{ 2 }-{ n }_{ 1 } }{ PC } \)
Following sign conventions, PO = -u, PI = +v and PC = +R in equation (6),
\(\frac { { n }_{ 2 } }{ -v } \) – \(\frac { { n }_{ 1 } }{ u } \) = \(\frac { \left( { n }_{ 2 }-{ n }_{ 1 } \right) }{ R } \)
After rearranging, finally we get,
\(\frac { { n }_{ 2 } }{ v } \) – \(\frac { { n }_{ 1 } }{ u } \) = \(\frac { \left( { n }_{ 2 }-{ n }_{ 1 } \right) }{ R } \) ……… (7)
Equation (7) gives the relation among the object distance n, image distance v, refractive indices of the two media (n1 and n2) and the radius of curvature R of the spherical surface. It holds for any spherical surface.
If the first medium is air then, n1 = 1 and the second medium is taken just as n2 = n, then the equation is reduced to,
\(\frac { n }{ v}\)–\(\frac { 1 }{ u}\) = \(\frac { \left( { n }-1 \right) }{ R } \) ………(8)
Question 7.
Obtain lens maker’s formula and mention its significance.
Answer:
Lens maker’s formula and lens equation:
Let us consider a thin lens made up of a medium of refractive index n2, is placed in a medium of refractive index n1. Let R1 and R2 be the radii of curvature of two spherical surfaces (1) and (2) respectively and P be the pole. Consider a point object O on the principal axis. The ray which falls very close to P, after refraction at the surface (1) forms image at I’. Before it does so, it is again refracted by the surface (2). Therefore the final image is formed at I. The general equation for the refraction at a spherical surface is given by
\(\frac { { n }_{ 2 } }{ v } \) – \(\frac { { n }_{ 1 } }{ u } \) = \(\frac { \left( { n }_{ 2 }-{ n }_{ 1 } \right) }{ R } \)
For the refracting surface (1), the light goes from n1ton2.
\(\frac { { n }_{ 2 } }{ v’ } \) – \(\frac { { n }_{ 1 } }{ u } \) = \(\frac { \left( { n }_{ 2 }-{ n }_{ 1 } \right) }{ R }_{ 1 } \) …….. (1)
For the refracting surface (2), the light goes from medium n2ton1.
\(\frac { { n }_{ 1 } }{ v } \) – \(\frac { { n }_{ 2 } }{ v’ } \) = \(\frac { \left( { n }_{ 1 }-{ n }_{ 2 } \right) }{ R }_{ 2 } \) …….. (2)
Adding the above two equation (1) and (2)
\(\frac { { n }_{ 1 } }{ v } \) – \(\frac { { n }_{ 1 } }{ u } \) = (n2 – n1) \(\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\)
Furhter simplifying and rearranging,
\(\frac { 1 }{ v }\)–\(\frac { 1 }{ u }\) = \(\left(\frac{n_{2}-n_{1}}{n_{1}}\right)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\)
\(\frac { 1 }{ v }\)–\(\frac { 1 }{ u }\) = \(\left(\frac{n_{2}}{n_{1}}-1\right)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\) ……….. (3)
If the object is at infinity, the image is formed at the focus of the lens. Thus, for u = ∞, v= f. Then the equation becomes.
\(\frac { 1 }{ f }\)–\(\frac { 1 }{ ∞ }\) = \(\left(\frac{n_{2}}{n_{1}}-1\right)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\)
\(\frac { 1 }{ f }\)=\(\left(\frac{n_{2}}{n_{1}}-1\right)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\) ………… (4)
If the refractive index of the lens is and it is placed in air, then n2 = n and n1 = 1 equation (4) becomes,
\(\frac { 1 }{ f }\) = (n-1) \(\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\) ………. (5)
The above equation is called the lens maker’s formula, because it tells the lens manufactures what curvature is needed to make a lens of desired focal length with a material of particular refractive index. This formula holds good also for a concave lens. By comparing the equations (3) and (4) we can write,
\(\frac { 1 }{ v }\)–\(\frac { 1 }{ u }\) =\(\frac { 1 }{ f }\) …… (6)
This equation is known as lens equation which relates the object distance u and image distance v with the focal length f of the lens. This formula holds good for a any type of lens.
Question 8.
Derive the equation for thin lens and obtain its magnification.
Answer:
Lateral magnification in thin lens:
Let us consider an object 00′ of height h1 placed on the principal axis with its height perpendicular to the principal axis. The ray Op passing through the pole of the lens goes undeviated. The inverted real image II’ formed has a height h2.
The lateral or transverse magnification m is defined as the ratio of the height of the image to that of the object.
m = \(\frac { II’ }{ OO’ }\) …….. (1)
From the two similar triangles ∆ POO’ and ∆ PII’, we can write,
\(\frac { H’ }{ OO’ }\) = \(\frac { PI }{ PO }\) ……..(2)
Applying sign convention,
\(\frac{-h_{2}}{h_{1}}\) = \(\frac { v }{ -u}\)
Substituting this in the equation (1) for magnification,
m = \(\frac{-h_{2}}{h_{1}}\) = \(\frac { v }{ -u}\)
After rearranging,
m = \(\frac{h_{2}}{h_{1}}\) = \(\frac { v }{ u}\) …….. (3)
The magnification is negative for real image and positive for virtual image. In the case of a concave lens, the magnification is always positive and less than one. We can also have the equations for magnification by combining the lens equation with the formula for magnification
as,
m = \(\frac{h_{2}}{h_{1}}=\frac{f}{f+u}\) (or) m = \(\frac{h_{2}}{h_{1}}=\frac{f-v}{f}\) ……… (4)
![]()
Question 9.
Derive the equation for effective focal length for lenses in out of contact.
Answer:
Consider a two lenses of focal length f1 and f2 arranged coaxially but separated by a distance d can be considered. For a parallel ray that falls on the arrangement, the two lenses produce deviations δ1 and δ2 respectively and The net deviation δ is,
δ = δ1 + δ2 ……. (1)
From Angle of deviation in lens equation, δ = \(\frac { h }{ f }\)
δ1 = \(\frac{h_{1}}{f_{1}}\); δ2 = \(\frac{h_{2}}{f_{2}}\) δ = \(\frac{h_{1}}{f}\) ….. (2)
The equation (1) becomes,
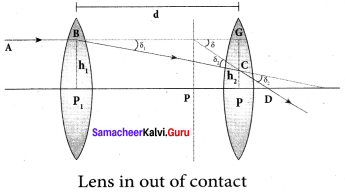
\(\frac{h_{1}}{f}\) = \(\frac{h_{1}}{f_{1}}\) + \(\frac{h_{2}}{f_{2}}\) ……. (3)
From the geometry,
h2 – h1 = P2C = CG
h2 – h1 = BG tan δ1 ≈ BG δ1
h2 – h1 = d\(\frac{h_{1}}{f_{1}}\)
h2 = h1 + d\(\frac{h_{1}}{f_{1}}\) …….. (4)
Substituting the above equation in Equation (3)
\(\frac{h_{1}}{f}=\frac{h_{1}}{f_{1}}+\frac{h_{1}}{f_{2}}+\frac{h_{1} d}{f_{1} f_{2}}\)
On further simplification,
\(\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}+\frac{d}{f_{1} f_{2}}\) …….. (5)
The above equation could be used to find the equivalent focal length.
Question 10.
Derive the equation for angle of deviation produced by a prism and thus obtain the equation for refractive index of material of the prism.
Answer:
Angie of deviation produced by prism:
Let light ray PQ is incident on one of the refracting faces of the prism. The angles of incidence and refraction at the first face AB are i1 and r1. The path of the light inside the prism is QR. The angle of incidence and refraction at the second face AC is r2 and i2 respectively. RS is the ray emerging from p the second face. Angle i2 is also called angle of emergence. The angle between the direction of the incident ray PQ and the emergent ray RS is called the angle of deviation d.
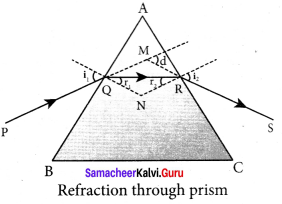
The two normals drawn at the point of incidence Q and emergence R are QN and RN. They meet at point N. The incident ray and the emergent ray meet at a point M.
The deviation d1 at the surface AB is,
angle ∠RQM = d1 = i1 – r1 …(1)
The deviation d2 at the surface AC is,
angle ∠QRM = d2 = i2 – r2 …(2)
Total angle of deviation d produced is,
d = d1 + d2 …(3)
Substituting for d1 and d2,
d=(i1 – r1) + (i2 – r2)
After rearranging,
d = (i1 – r1) + (i2 – r2) …(4)
In the quadrilateral AQNR, two of the angles (at the vertices Q and R) are right angles. Therefore, the sum of the other angles of the quadrilateral is 180°.
∠A + ∠QNR = 180° …(5)
From the triangle ∆QNR,
r1+ r2 ∠QNR = 180° …(6)
Comparing these two equations (5) and (6) we get,
r1+ r2 = A …(7)
Substituting this in equation (4) for angle of deviation,
d= i1+ i2 -A …(8)
Thus, the angle of deviation depends on the angle of incidence angle of emergence and the angle for the prism.
Refractive index of the material of the prism:
At minimum deviation,
i1 = i2 = i and r1 = r2 = r
Now, the equation (8) becomes,
D = i1 + i2-A (or) i = \(\frac { \left( A+D \right) }{ 2 } \)
The equation (7) becomes,
r1 + r2 = A ⇒ 2r = A (or) r = \(\frac { A }{ 2 }\)
Substituting i and r in Snell’s law,
n = \(\frac { sin i }{ sin r }\)
n = \(\frac{\sin \left(\frac{A+D}{2}\right)}{\sin \left(\frac{A}{2}\right)}\)
The above equation is used to find the refractive index of the material of the prism.
Question 11.
What is dispersion? Obtain the equation for dispersive power of a medium.
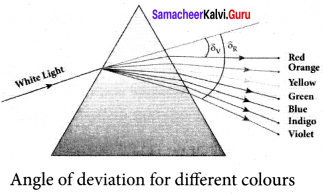
Answer:
Dispersion. Dispersion is splitting of white light into its constituent colours.
Dispersive Power:
Consider a beam of white light passes through a prism; It gets dispersed into its constituent colours. Let δV, δR are the angles of deviation for violet and red light. Let nV and nR are the refractive indices for the violet and red light respectively.
The refractive index of the material of a prism is given by the equation
n = \(\frac{\sin \left(\frac{A+D}{2}\right)}{\sin \left(\frac{A}{2}\right)}\)
Here A is the angle of the prism and D is the angle of minimum deviation. If the angle of prism is small of the order of 10°, the prism is said to be a small angle prism. When rays of light pass through such prisms, the angle of deviation also becomes small. If A be the angle of a small angle prism and 5 the angle of deviation then the prism formula becomes.
n = \(\frac{\sin \left(\frac{A+\delta}{2}\right)}{\sin \left(\frac{A}{2}\right)}\) ……… (1)
For small angles of A and δm,
\(\sin \left(\frac{\mathrm{A}+\delta}{2}\right) \approx\left(\frac{\mathrm{A}+\delta}{2}\right)\) ……. (2)
\(\sin \left(\frac{\mathrm{A}}{2}\right) \approx\left(\frac{\mathrm{A}}{2}\right)\) …… (3)
∴ n = \(\frac{\left(\frac{A+\delta}{2}\right)}{\left(\frac{A}{2}\right)}=\frac{A+\delta}{A}=1+\frac{\delta}{A}\)
Further simplifying, \(\frac { δ }{ A }\) = n – 1
δ = (n – 1) A ……. (4)
When white light enters the prism, the deviation is different for different colours. Thus, the refractive index is also different for different colours.
For Violet light, δV = (nV – 1)A …(5)
For Red light, δR = (nR – 1) …(6)
As, angle of deviation for violet colour δV is greater than angle of deviation for red colour δR, the refractive index for violet colour nV is greater than the refractive index for red colour nR. Subtracting δV from δR we get,
δV – δR = (nV – nR)A ….. (7)
The term (δV – δR) is the angular separation between the two extreme colours (violet and red) in the spectrum is called the angular dispersion. Clearly, the angular dispersion produced by a prism depends upon.
- Angle of the prism
- Nature of the material of the prism.
If we take 8 is the angle of deviation for any middly ray (green or yellow) and n the corresponding refractive index. Then,
8 = (n – 1) A … (8)
Dispersive power (ω) is the ability of the material of the prism to cause dispersion. It is defined as the ratio of the angular dispersion for the extreme colours to the deviation for any mean colour. Dispersive power (ω),
![]()
Substituting for (δV-δR)and (δ),
ω = \(\frac{\left(n_{\mathrm{V}}-n_{\mathrm{R}}\right)}{(n-1)}\) ……. (10)
Dispersive power is a dimensionless quality. It has no unit. Dispersive power is always positive. The dispersive power of a prism depends only on the nature of material of the prism and it is independent of the angle of the prism.
![]()
Question 12.
Prove laws of reflection using Huygens’ principle.
Answer:
Proof for laws of reflection using Huygens’ Principle:
Let us consider a parallel beam of light, incident on a reflecting plane surface such as a plane mirror XY. The incident wavefront is AB and the reflected wavefront is A’B’ in the same medium. These wavefronts are perpendicular to the incident rays L, M and reflected rays L’, M’ respectively.
By the time point A of the incident wavefront touches the reflecting surface, the point B is yet to travel a distance BB’ to touch the reflecting surface a B’. When the point B falls on the reflecting surface at B’ , the point A would have reached A’. This is applicable to all the points on the wavefront.
Thus, the reflected wavefront A’B’ emanates as a plane wavefront. The two normals N and N’ are considered at the points where the rays L and M fall on the reflecting surface. As reflection happens in the same medium, the speed of light is same before and after the reflection. Hence, the time taken for the ray to travel from B to B’ is the same as the time taken for the ray to travel from A to A’. Thus, the distance BB’ is equal to the distance AA’; (AA’= BB’).
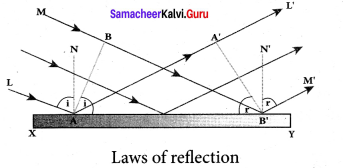
(i) The incident rays, the reflected rays and the normal are in the same plane.
(ii) Angle of incidence,
∠i = ∠NAL = 90° – ∠NAB = ∠BAB’
Angle of reflection,
∠r = ∠N’B’M’ = 90° – ∠N’B’A’ = ∠A’B’A
For the two right angle triangles, A ABB’ and A B’A’A, the right angles, ∠B and ∠A’ are equal, (∠B and ∠A’ = 90°); the two sides, AA’ and BB’ are equal, (AA’ = BB’); the side AB’ is the common. Thus, the two triangles are congruent. As per the property of congruency, the two angles, ∠BAB’ and ∠A’B’A must also be equal. i = r
Hence, the laws of reflection are proved.
Question 13.
Prove laws of refraction using Huygens’ principle.
Answer:
Let us consider a parallel beam of light is incident on a refracting plane surface XY such as a glass surface. The incident wavefront AB is in rarer medium (1) and the refracted wavefront A’B’ is in denser medium (2). These wavefronts are perpendicular to the incident rays L, M and refracted rays L’, M’ respectively. By the time the point A of the incident wavefront touches the refracting surface, the point B is yet to travel a distance BB’ to touch the refracting surface at B’
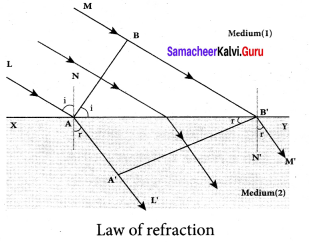
When the point B falls on the refracting surface at B’, the point A’ would have reached A in the other medium. This is applicable to all the points on the wavefront. Thus, the refracted wavefront A’B’ emanates as a plane wavefront.
The two normals N and N’ are considered at the points where the rays L and M fall on the refracting surface. As refraction happens from rarer medium (1) to denser medium (2), the speed of light is v1 and v2 before and after refraction and v1 is greater than v2 (v1 > v2). But, the time taken t for the ray to travel from B to B’ is the same as the time taken for the ray to
travel from A to A’.
t = \(\frac { BB’ }{ { v }_{ 1 } } \) = \(\frac { AA’ }{ { v }_{ 2 } } \) (or) \(\frac { BB’ }{ AA’ }\) = \(\frac { { v }_{ 1 } }{ { v }_{ 2 } } \)
(i) The incident rays, the refracted rays and the normal are in the same plane.
(ii) Angle of incidence,
i = ∠NAL = 90° – ∠NAB = ∠BAB’
Angle of refraction,
r =∠N’B’M’ = 90° – ∠N’B’A’ = ∠A’B’A’
For the two right angle triangles ∆ ABB’ and ∆ B’A’A,
\(\frac { sin i }{ sin r }\) = \(\frac{B B^{\prime} / A B^{\prime}}{A A^{\prime} / A B^{\prime}}\) =\(\frac { BB’ }{ AA’ }\) =\(\frac{v_{1}}{v_{2}}=\frac{c / v_{2}}{c / v_{1}}\)
Here, c is speed of light in vacuum. The ratio c/v is the constant, called refractive index of the medium. The refractive index of medium (1) is, c/v1 = n1 and that of medium (2) is, c/v2 = n2.
\(\frac { sin i }{ sin r }\) = \(\frac { { n }_{ 2 } }{ { n }_{ 1 } } \)
In product form,
n1 sin i = n2 sin r
Hence, the laws of refraction are proved.
Question 14.
Obtain the equation for resultant intensify’ due to interference of light.
Answer:
Let us consider two light waves from the two sources S1 and S2 meeting at a point P. The wave from S1 at an instant t at P is,
y1 = a1 sin ωt … (1)
The wave form S2 at an instant t at P is,
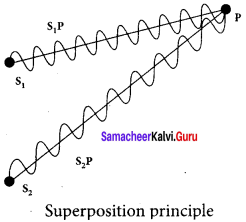
y2 = a2 sin (ωt + Φ) … (2)
The two waves have different amplitudes a1 and a2, same angular frequency ω, and a phase difference of Φ between them. The resultant displacement will be given by,
y = y1 + y2 = a1 sin ωt + a1 sin2 (ωt + Φ) … (3)
The simplification of the above equation by using trigonometric identities gives the equation,
y = A sin (ωt + θ) … (4)
Where, A = \(\sqrt{a_{1}^{2}+a_{2}^{2}+2 a_{1} a_{2} \cos \phi}\) …. (5)
θ = tan-1 \(\frac{a_{2} \sin \phi}{a_{1}+a_{2} \cos \phi}\) …. (6)
The resultant amplitude is maximum,
Amax = \(\sqrt{\left(a_{1}+a_{2}\right)^{2}}\) ; when Φ = 0, ±2π, ±4π …., …… (7)
The resultant amplitude is minimum,
Amax = \(\sqrt{\left(a_{1}-a_{2}\right)^{2}}\) ; when Φ = ±π, ±3,π ±5π …., …… (8)
The intensity of light is proportional to square of amplitude,
I ∝ A2 ….. (9)
Now, equation (5) becomes,
I ∝ I1+I 2+2 \(\sqrt { { I }_{ 1 }{ I }_{ 2 } } \) cos Φ …… (10)
In equation (10) if the phase difference, Φ = 0, ±2π, ±4π …., it corresponds to the condition for maximum intensity of light called as constructive interference. The resultant maximum intensity is,
Imax ∝ ( a1 + a2)2 ∝ I1 + I2 +2 \(\sqrt { { I }_{ 1 }{ I }_{ 2 } } \) …… (11)
In equation (10) if the phase difference, Φ = ±π, ±3,π ±5π …., it corresponds to the condition for minimum intensity of light called destructive interference. The resultant minimum intensity is,
Imax ∝( a1 – a2)2 ∝ I1 + I2 -2 \(\sqrt { { I }_{ 1 }{ I }_{ 2 } } \) ……. (12)
![]()
Question 15.
Explain the Young’s double slit experimental setup and obtain the equation for path difference.
Answer:
I Experimental setup:
1. Wavefronts from S1 and S2 spread out and overlapping takes place to the right side of double slit. When a screen is placed at a distance of about 1 meter s from the slits, alternate bright and dark fringes which are equally spaced appear on the screen. These are called interference fringes or bands.
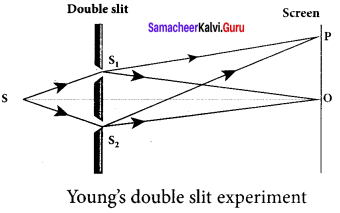
2. Using an eyepiece the fringes can be seen directly. At the center point O on the screen, waves from S1 and S2 travel equal distances and arrive in-phase. These two waves constructively interfere and bright fringe is observed at O. This is called central bright fringe.
3. The fringes disappear and there is uniform illumination on the screen when one of the slits is covered. This shows clearly that the bands are due to interference.
II Equation for path difference:
1. Let d be the distance between the double slits S1 and S2 which act as coherent sources of wavelength λ. A screen is placed parallel to the double slit at a distance D from it. The mid-point of S1 and S2 is C and the midpoint of the screen O is equidistant from S1 and S2. P is any point at a distance y from O.
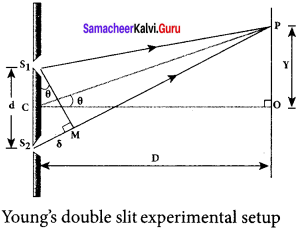
2. The waves from S1 and S2 meet at P either inphase or out-of-phase depending upon the path difference between the two waves.
3. The path difference δ between the light waves from S1 and S2 to the point P is,
δ = S2 P – S1
4. A perpendicular is dropped from the point S1 to the line S2 P at M to find the path difference more precisely.
δ = S2 P – MP = S2 M
The angular position of the point P from C is θ. ∠OCP = θ.
From the geometry, the angles ∠OCP and ∠S2 S1M are equal. ∠OCP = ∠S2 S1 M = θ
In right angle triangle ∆S1 S2 M, the path difference, S2 M = d sin θ
δ = d sin θ
If the angle 0 is small, sin θ ≈ tan θ ≈ θ. From the right angle triangle ∆OCP, tan θ = \(\frac { y }{ D }\)
The path difference, δ = \(\frac { dy }{ D }\)
Question 16.
Obtain the equation for bandwidth in Young’s double slit experiment.
Answer:
Condition for bright fringe (or) maxima
The condition for the constructive interference or the point P to be have a bright fringe is,
Path difference, δ = nλ
where, n = 0, 1, 2,. . .
∴ \(\frac { dy }{ D }\) = nλ
y = n \(\frac { λD }{ d }\) (or) yn = n \(\frac { λD }{ d }\)
This is the condition for the point P to be a bright fringe. The distance is the distance of the nth bright fringe from the point O.
Condition for dark fringe (or) minima
The condition for the destructive interference or the point P to be have a dark fringe is,
Path difference, δ = (2n – 1) \(\frac { λ }{ 2 }\)
where, n = 1, 2, 3 …
∴ \(\frac { dy }{ D }\) = (2n – 1) \(\frac { λ }{ 2 }\)
y = \(\frac { (2n-1) }{ 2 }\) \(\frac { λD }{ d }\) (or) yn = \(\frac { (2n-1) }{ 2 }\) \(\frac { λD }{ d }\)
Equation for bandwidth
The bandwidth (β) is defined as the distance between any two consecutive bright or dark fringes.
The distance between (n +1)th and nth consecutive bright fringes from O is given by,
β = y(n +1) – yn = \(\left((n+1) \frac{\lambda \mathrm{D}}{d}\right)-\left(n \frac{\lambda \mathrm{D}}{d}\right)\)
β = \(\frac { λD }{ d }\)
Similarly, the distance between (n +1)th and nth consecutive dark fringes from O is given by,
β = y(n+1) – yn = \(\left(\frac{(2(n+1)-1)}{2} \frac{\lambda D}{d}\right)-\left(\frac{(2 n-1)}{2} \frac{\lambda D}{d}\right)\)
β = \(\frac { λD }{ d }\)
The above equation show that the bright and dark fringes are of same width equally spaced on either side of central bright fringe.
Question 17.
Obtain the equations for constructive and destructive interference for transmitted and reflected waves in thin films.
Answer:
Interference in thin films:
Let us consider a thin film of transparent material of refractive index p (not to confuse with order of fringe n) and thickness d. A parallel beam of light is incident on the film at an angle i. The wave is divided into two parts at the upper surface, one is reflected and the other is refracted.
The refracted part, which enters into the film, again gets divided at the lower surface into two parts; one is transmitted out of the film and the other is reflected back in to the film. Reflected as well as refracted waves are sent by the film as multiple reflections take place inside the film. The interference is produced by both the reflected and transmitted light.
For transmitted light:
The light transmitted may interfere to produce a resultant intensity. Let us consider the path difference between the two light waves transmitted from B and D. The two waves moved together and remained in phase up to B where splitting occured. The extra path travelled by the wave transmitted from D is the path inside the film, BC + CD.
If we approximate the incidence to be nearly normal (i = 0), then the points B and D are very close to each other. The extra distance travelled by the wave is approximately twice thickness of the film, BC + CD = 2d. As this extra path is traversed in a medium of refractive index µ, the optical path difference is, δ = 2µd.
The condition for constructive interference in transmitted ray is,
2µd = nλ
Similarly, the condition for destructive interference in transmitted ray is,
2µd = (2n – 1) \(\frac { λ }{ 2 }\)
For reflected light:
It is experimentally and theoretically proved that a wave while travelling in a rarer medium and getting reflected by a denser medium, undergoes a phase change of π. Hence, an additional path difference of \(\frac { λ }{ 2 }\) should be considered.
Let us consider the path difference between the light waves reflected by the upper surface at A and the other wave coming out at C after passing through the film. The additional path travelled by wave coming out from C is the path inside the film, AB + BC. For nearly normal incidence this distance could be approximated as, AB + BC = 2d. As this extra path is travelled in the medium of refractive index p, the optical path difference is, δ = 2µd.
The condition for constructive interference for reflected ray is,
2µd + \(\frac { λ }{ 2 }\) = nλ (or) 2µd = (2n – 1) \(\frac { λ }{ 2 }\)
The additional path difference \(\frac { λ }{ 2 }\) is due to the phase change of n in rarer to denser reflection taking place at A. The condition for destructive interference for reflected ray is,
2µd + \(\frac { λ }{ 2 }\) = (2n + 1) \(\frac { λ }{ 2 }\) (or) 2µd = nλ
Question 18.
Discuss diffraction at single slit and obtain the condition for nth minimum.
Answer:
Diffraction at single slit:
Let a parallel beam of light fall normally on a single slit AB of width. The diffracted beam falls on a screen kept at a distance. The center of the slit is C. A straight line through C perpendicular to the plane of slit meets the center of the screen at O. We would like to find the intensity at any point P on the screen. The lines joining P to the different points on the slit can be treated as parallel lines, making an angle 9 with the normal CO.
All the waves start parallel to each other from different points of the slit and interfere at point P and other points to give the resultant intensities. The point P is in the geometrically shadowed region, up to which the central maximum is spread due to diffraction. We need to give the condition for the point P to be of various minima.
The basic idea is to divide the slit into much smaller even number of parts. Then, add their contributions at P with the proper path difference to show that destructive interference takes place at that point to make it minimum. To explain maximum, the slit is divided into odd number of parts.
Condition for P to be first minimum:
Let us divide the slit AB into two half’s AC and CB. Now the width of AC is (a/2). We have different points on the slit which are separated by the same width (here a/2) called corresponding points.
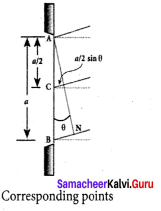
The path difference of light waves from different corresponding points meeting at point P and interfere destructively to make it first minimum. The path difference 8 between waves from these corresponding points
is, δ = \(\frac { a }{ 2 }\) sin θ
The condition for P to be first minimum, \(\frac { a }{ 2 }\) sin θ = \(\frac { λ }{ 2 }\)
a sin θ = λ (first minimum) ….. (1)
Condition for P to be first minimum:
Let us divide the slit AB into two half’s AC and CB. Now the width of AC is (a/2). We have different points on the slit which are separated by the same width (here a/2) called corresponding points.
The path difference of light waves from different corresponding points meeting at point P and interfere destructively to make it first minimum.
The path difference δ between waves from these corresponding points δ = \(\frac { a }{ 4 }\) sin θ.
The condition for P to be first minimum, \(\frac { a }{ 4 }\) sin θ = \(\frac { λ }{ 2 }\)
a sin θ = 2λ (second minimum) …(2)
Condition for P to be third order minimum:
The same way the slit is divided into six equal parts to explain the condition for P to be third
minimum is, \(\frac { a }{ 6 }\) sin θ = \(\frac { λ }{ 2 }\)
a sin θ = 3λ (third minimum) …(3)
Condition for P to be nth order minimum:
Dividing the slit into 2n number of (even number of) equal parts makes the light produced by one of the corresponding points to be cancelled by its counterpart. Thus, the condition for nth
order minimum is, \(\frac { a }{ 2n }\) sin θ = \(\frac { λ }{ 2 }\)
a sin θ = nλ (nth minimum)
![]()
Question 19.
Discuss the diffraction at a grating and obtain the condition for the mth maximum.
Answer:
A plane transmission grating is represented by AB. Let a plane wavefront of monochromatic light with wavelength λ be incident normally on the grating. As the slits size is comparable to that of wavelength, the incident light diffracts at the grating.
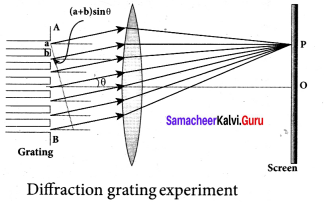
A diffraction pattern is obtained on the screen when the diffracted waves are focused on a screen using a convex lens. Let us consider a point P at an angle 0 with the normal drawn from the center of the grating to the screen. The path difference 5 between the diffracted waves from one pair of corresponding points is,
δ = (a + b) sin θ
This path difference is the same for any pair of corresponding points. The point P will be bright, when
δ = m λ where m = 0, 1 , 2, 3
Combining the above two equations, we get,
(a + b) sin θ = m λ
Here, m is called order of diffraction.
Condition for zero order maximum, m = 0
For (a + b) sin θ = 0, the position, θ = 0. sin θ = 0 and m = 0. This is called zero order diffraction or central maximum.
Condition for first order maximum, m = 1
If (a + b) sin θ1 = λ, the diffracted light meet at an angle θ1 to the incident direction and the first order maximum is obtained.
Condition for second order maximum, m = 2
Similarly, (a + b) sin θ2 = 2λ, forms the second order maximum at the angular position θ2.
Condition for higher order maximum
On either side of central maxima different higher orders of diffraction maxima are formed at different angular positions.
If we take, N = \(\frac { 1 }{ a+b }\)
Then, N gives the number of grating elements or rulings drawn per unit width of the grating. Normally, this number N is specified on the grating itself. Now, the equation becomes,
\(\frac { 1 }{ N }\) sin θ = mλ, (or) sin θ = Nmλ
Question 20.
Discuss the experiment to determine the wavelength of monochromatic light using diffraction grating.
Answer:
Experiment to determine the wavelength of monochromatic light:
The wavelength of a spectral line can be very accurately determined with the help of a diffraction grating and a spectrometer. Initially all the preliminary adjustments of the spectrometer are made. The slit of collimator is illuminated by a monochromatic light, whose wavelength is to be determined. The telescope is brought in line with collimator to view the image of the slit. The given plane transmission grating is then mounted on the prism table with its plane perpendicular to the incident beam of light coming from the collimator.
The telescope is turned to one side until the first order diffraction image of the slit coincides with the vertical cross wire of the eye piece. The reading of the position of the telescope is noted. Similarly the first order diffraction image on the other side is made to coincide with the vertical cross wire and corresponding reading is noted. The difference between two positions gives 2θ. Half of its value gives θ, the diffraction angle for first order maximum. The wavelength of light is calculated from the equation,
λ = \(\frac { sin θ }{ N m}\)
Here, N is the number of rulings per metre in the grating and m is the order of the diffraction image.
Question 21.
Discuss the experiment to determine the wavelength of different colours using diffraction grating.
Answer:
Determination of wavelength of different colours:
When white light is used, the diffraction pattern consists of a white central maximum and on both sides continuous coloured diffraction patterns are formed. The central maximum is white as all the colours meet here constructively with no path difference.
As θ increases, the path difference, (a + b) sin θ, passes through condition for maxima of diffraction of different orders for all colours from violet to red. It produces a spectrum of diffraction pattern from violet to red on either side of central maximum. By measuring the angle at which these colours appear for various orders of diffraction, the wavelength of different colours could be calculated using the formula,
λ = \(\frac { sin θ }{ N m}\)
Here, N is the number of rulings per metre in the grating and m is the order of the diffraction image.
Question 22.
Obtain the equation for resolving power of optical instrument.
Answer:
Resolution:
The effect of diffraction has an adverse impact in the image formation by the optical instruments such as microscope and telescope. For a single rectangular slit, the half angle θ subtended by the spread of central maximum (or position of first minimum) is given by the ‘ relation,
a sin θ = λ … (1)
Similar to a rectangular slit, when a circular aperture or opening (like a lens or the iris of our eye) forms an image of a point object, the image formed will not be a point but a diffraction pattern of concentric circles that becomes fainter while moving away from the center. These are known as Airy’s discs. The circle of central maximum has the half angular spread given by the equation,
a sin θ = 1.22λ … (2)
Here, the numerical value 1.22 comes for central maximum formed by circular apertures. This involves higher level mathematics which is avoided in this discussion.
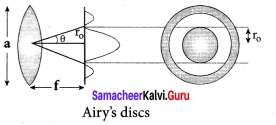
For small angles, sin θ ≈ θ
a θ = 1.22λ … (3)
Rewriting further, θ = \(\frac { 1.22λ }{ a}\) and \(\frac { { r }_{ 0 } }{ f } \) = \(\frac { 1.22λ }{ a}\)
r0 = \(\frac { 1.22λf }{ a}\) …. (4)
When two point sources close to each another form image on the screen, the diffraction pattern of one point source can overlap with another and produce a blurred image. To obtain a good image of the two sources, the two point sources must be resolved i.e., the point sources must be imaged in such a way that their images are sufficiently far apart that their diffraction patterns do not overlap.
According to Rayleigh’s criterion, for two point objects to be just resolved, the minimum distance between their diffraction images must be in such a way that the central maximum of one coincides with the first minimum of the other and vice versa. Such an image is said to be just resolved image of the object. The Rayleigh’s criterion is said to be limit of resolution.
According to Rayleigh’s criterion the two point sources are said to be just resolved when the distance between the two maxima is at least r0. The angular resolution has a unit in radian (rad) and it is given by the equation.
θ = \(\frac { 1.22λf}{ a}\)
It shows that the first order diffraction angle must be as small as possible for greater resolution. This further shows that for better resolution, the wavelength of light used must be as small as possible and the size of the aperture of the instrument used must be as large as possible. The equation (4) is used to calculate spacial resolution. The inverse of resolution is called resolving power. This implies, smaller the resolution, greater is the resolving power of the instrument. The ability of an optical instrument to • separate or distinguish small or closely adjacent objects through the image formation is said to be resolving power of the instrument.
![]()
Question 23.
Discuss about simple microscope and obtain the equations for magnification for near point focusing and normal focusing.
Answer:
Simple microscope:
A simple microscope is a single magnifying (converging) lens of small focal length. The idea is to get an erect, magnified and virtual image of the object. For this the object is placed between F and P on one side of the lens and viewed from other side of the lens. There are two magnifications to be discussed for two kinds of focusing.
- Near point focusing :
The image is formed at near point, i.e. 25 cm for normal eye. This distance is also called as least distance D of distinct vision. In this position, the eye feels comfortable but there is little strain on the eye. - Normal focusing :
The image is formed at infinity. In this position the eye is most relaxed to view the image.
Magnification in near point focusing:
Object distance u is less than f. The image distance is the near point D. The magnification m is given by the relation,
m = \(\frac { v}{ u}\)
With the help of lens equation, \(\frac { 1}{ v}\) – \(\frac { 1}{ u}\) \(\frac { 1}{ f}\) the magnification can further be writen as,
m = 1- \(\frac { v}{ f}\)
Substituting for v with sign convention, v = -Derivem
m = 1 + \(\frac { D}{ f}\)
This is the magnification for near point focusing
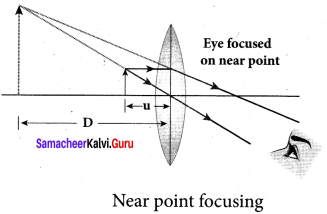
Magnification in normal focusing (angular magnification):
We will now find the magnification for the image formed at infinity. If we take the ratio of height of image to height of object \(\left(m=\frac{h^{\prime}}{h}\right)\) to find the magnification, we will not get a practical relation as the image will also be of infinite size when the image is formed at infinity. Hence, we can practically use the angular magnification. The angular magnification is defined as the ratio of angle 0j subtended by the image with aided eye to the angle 90 subtended by the object with unaided eye.
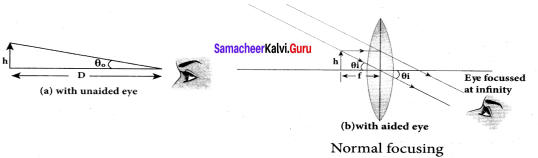
m = \(\frac{\theta_{i}}{\theta_{0}}\)
For unaided eye, tan θ0 ≈ θ0 = \(\frac { h }{ D }\)
For aided eye, tan θi ≈ θi = \(\frac { h }{ f }\)
The angular magnification is, m = \(\frac{\theta_{i}}{\theta_{0}}\) = \(\frac { h/f }{ h/d }\)
m = \(\frac { d }{ f }\)
This is the magnification for normal focusing. The magnification for normal focusing is one less than that for near point focusing.
Question 24.
Explain about compound microscope and obtain the equation for magnification. Compound microscope:
Answer:
The lens near the object, called the objective, forms a real, inverted, magnified image of the object. This serves as the object for the second lens which is the eyepiece. Eyepiece serves as a simple microscope that produces finally an enlarged and virtual image. The first inverted image formed by the objective is to be adjusted close to, but within the focal plane of the eyepiece so that the final image is formed nearly at infinity or at the near point. The final image is inverted with respect to the original object. We can obtain the magnification for a compound microscope.
Magnification of compound microscope :
From the ray diagram, the linear magnification due to the objective is,
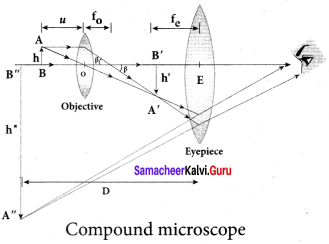
m0 = \(\frac { h’ }{ f}\)
From the figure, tan β = \(\frac { h }{ { f }_{ 0 } } \) =\(\frac { h’ }{ L’}\),then
\(\frac { h’ }{ h}\) = \(\frac { L }{ { f }_{ 0 } } \); m0 =\(\frac { L }{ { f }_{ 0 } } \)
Here, the distance L is between the first focal point of the eyepiece to the second focal point of the objective. This is called the tube length
L of the microscope as f0 and fe are comparatively smaller than L. If the final image is formed at P (near point focusing), the magnification me of the eyepiece is,
me = 1 + \(\frac { D }{ { f }_{ e } } \)
The total magnification m in near point focusing is,
m = m0me = \(\left(\frac{L}{f_{o}}\right)\left(1+\frac{D}{f_{e}}\right)\)
If the final image is formed at infinity (normal focusing), the magnification me of the eyepiece is,
me = \(\frac { D }{ { f }_{ e } } \)
The total magnification m in normal focusing is,
m = m0me = \(\left(\frac{L}{f_{o}}\right)\left(\frac{D}{f_{e}}\right)\)
Question 25.
Obtain the equation for resolving power of microscope.
Answer:
Resolving power of microscope:
The diagram related to the calculation of resolution of microscope. A microscope is used to see the details of the object under observation. The ability of microscope depends not only in magnifying the object but also in resolving two points on the object separated by a small distance dmin.
Smaller the value of dmin better will be the resolving power of the microscope.
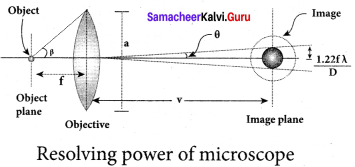
The radius of central maxima is, r0 = \(\frac { 1.22λv }{ a }\)
In the place of focal length f we have the image distance v. If the difference between the two points on the object to be resolved is dmin, then the magnification m is, m = \(\frac{r_{o}}{d_{\min }}\)
dmin = \(\frac{r_{o}}{m}\) =\(\frac{1.22 \lambda v}{a m}\) = \(\frac{1.22 \lambda v}{a(v / u)}\) = \(\frac{1.22 \lambda u}{a}\) [∴m = v/u] [∴ [u ≈ ƒ]
On the object side, 2tan β ≈ 2sin β = \(\frac { a }{ f }\)
dmin = \(\frac{1.22 \lambda}{2 sin β }\) ∴ [a = ƒ2 sinβ]
To further reduce the value of dmin the optical path of the light is increased by immersing the objective of the microscope in to a bath containing oil of refractive index n.
dmin = \(\frac{1.22 \lambda}{2n sin β }\)
Such an objective is called oil immersed objective. The term n sin p is called numerical aperture NA.
dmin = \(\frac{1.22 \lambda}{2(NA) }\)
Question 26.
Discuss about astronomical telescope.
Answer:
Astronomical telescope:
An astronomical telescope is used to get the magnification of distant astronomical objects like stars, planets, moon etc. the image formed by astronomical telescope will be inverted. It has an objective of long focal length and a much larger aperture than the eyepiece. Light from a distant object enters the objective and a real image is formed in the tube at its second focal point. The eyepiece magnifies this image producing a final inverted image.
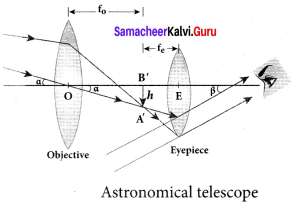
Magnification of astronomical telescope:
The magnification m is the ratio of the angle β subtended at the eye by the final image to the angle a which the object subtends at the lens or the eye
m = \(\frac { β }{ α }\)
From the diagram, m = \(\frac{h / f_{e}}{h / f_{0}}\)
m = \(\frac { { f }_{ 0 } }{ { f }_{ e } } \)
The length of the telescope is approximately, L = f0 + fe
Question 27.
Mention different parts of spectrometer and explain the preliminary adjustments. Spectrometer:
Answer:
The spectrometer is an optical instrument used to study the spectra of different sources of light and to measure the refractive indices of materials. It consists of basically three parts. They are (i) collimator, (ii) prism table and (iii) Telescope.
Adjustments of the spectrometer:
The following adjustments must be made before doing the experiment using spectrometer.
(a) Adjustment of the eyepiece:
The telescope is turned towards an illuminated surface and the eyepiece is moved to and fro until the cross wires are clearly seen.
(b) Adjustment of the telescope:
The telescope is adjusted to receive parallel rays by turning it towards a distant object and adjusting the distance between the objective lens and the eyepiece to get a clear image on the cross wire.
(c) Adjustment of the collimator:
The telescope is brought along the axial line with the collimator. The slit of the collimator is illuminated by a source of light. The distance between the slit and the lens of the collimator is adjusted until a clear image of the slit is seen at the cross wire of the telescope. Since the telescope is already adjusted for parallel rays, a well-defined image of the slit can be formed, only when the light rays emerging from the collimator are parallel.
(d) Levelling the prism table:
The prism table is adjusted or levelled to be in horizontal position by means of levelling screws and a spirit level.
![]()
Question 28.
Explain the experimental determination of material of the prism using spectrometer. Determination of refractive index of material of the prism:
Answer:
The preliminary adjustments of the telescope, collimator and the prism table of the spectrometer are made. The refractive index of the prism can be determined by knowing the angle of the prism and the angle of minimum deviation.
(i) Angle of the prism (A):
The prism is placed on the prism table with its refracting edge facing the collimator. The slit is illuminated by a sodium light (monochromotic light). The parallel rays coming from the collimator fall on the two faces AB and AC. The telescope is rotated to the position T1 until the image of the slit formed by the reflection at the face AB is made to coincide with the vertical cross wire of the telescope.
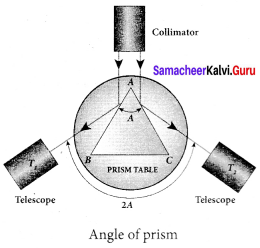
The readings of the verniers are noted. The telescope is then rotated to the position T2 where the image of the slit formed by the reflection at the face AC coincides with the vertical cross wire. The readings are again noted.
The difference between these two readings gives the angle rotated by the telescope, which is twice the angle of the prism. Half of this value gives the angle of the prism A.
(ii) Angle of minimum deviation (D):
The prism is placed on the prism table so that the light from the collimator falls on a refracting face, and the refracted image is observed through the telescope. The prism table is now rotated so that the angle of deviation decreases. A stage comes when the image stops for a moment and if we rotate the prism table further in the same direction, the image is seen to recede and the angle of deviation increases. The vertical cross wire of the telescope is made to coincide with the image of the slit where it turns back. This gives the minimum deviation position.
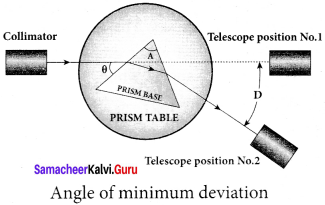
The readings of the verniers are noted. Now, the prism is removed and the telescope is turned to receive the direct ray and the vertical cross wire is made to coincide with the image. The readings of the verniers are noted. The difference between the two readings gives the angle of minimum deviation D. The refractive index of the material of the prism n is calculated using the formula,
n = \(\frac{\sin \left(\frac{A+D}{2}\right)}{\sin \left(\frac{A}{2}\right)}\)
The refractive index of a liquid may be determined in the same way using a hollow glass prism filled with the given liquid.
Samacheer Kalvi 12th Physics Optics Conceptual Questions
Question 1.
Why are dish antennas curved?
Answer:
Dish antenna is curved so as it can receive parallel signal rays coming from same direction. These parallel signal rays reflect from parabolic dish, and gathered at main antenna part. This increases directivity of antenna, and gives sufficient amplitude signal.
Question 2.
What type of lens is formed by a bubble inside water?
Answer:
Air bubble has spherical surface and is surrounded by medium (water) of higher refractive index. When light passes from water to air it gets diverged. So air bubble behaves as a concave lens.
Question 3.
It is possible for two lenses to produce zero power?
Answer:
Yes. It is possible for two lenses to produce zero power. Both the surfaces of lenses are equally curved, i.e. R1 = R2 and hence
Power (P) = (µ – 1) \(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)=0\)
Question 4.
Why does sky look blue and clouds look white?
Answer:
Blue colour of the sky is due to scattering of sunlight by air molecules. According to Rayleigh’s law, intensity of scattered light, I ∝ \(\frac { 1 }{ { \lambda }^{ 4 } } \). So blue light of shorter wavelength is scattered much more than red light of larger wavelength. The blue component is proportionally more in light coming from different parts of the sky. That is why the sky appear blue. Clouds have large particles like dust and water droplets which scatter light of all colours almost equally. Hence clouds generally appear white.
Question 5.
Why is yellow light preferred to during fog?
Answer:
Yellow light has longer wavelength than green, blue or violet components of white lights. As scattered intensity, I ∝ \(\frac { 1 }{ { \lambda }^{ 4 } } \). so yellow colour is least scattered and produces sufficient illumination.
![]()
Question 6.
Two independent monochromatic sources cannot act as coherent sources, why?
Answer:
Two independent sources of light cannot be coherent. This is because light is emitted by individual atoms. When they return to ground state. Even the smallest source of light contains billions of atoms which obviously cannot emit light waves in the same phase.
Question 7.
Does diffraction take place at the Young’s double slit?
Answer:
Both diffraction and interference in the double slit experiment. The wavefront is diffracted as it passes through each of the slits. The diffraction causes the wavefronts to spread out as if they were coming from light sources located at the slits. These two wavefronts overlap, and interference occurs.
Question 8.
Is there any difference between colored light obtained from prism and colours of soap bubble?
Answer:
Yes. there is a difference between colored light obtained from the prism is the phenomenon of‘dispersion of light’ and colored light obtained from the soap bubble is the phenomenon of ‘interference of light’.
Question 9.
A small disc is placed in the path of the light from distance source. Will the center of the shadow be bright or dark?
Answer:
When a tiny circular small disc is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the disc because, wave diffracted from the edge of the circular disc interface constructively at the centre of the shadow, which produces bright spot.
Question 10.
When a wave undergoes reflection at a denser medium, what happens to its phase?
Answer:
When a wave undergoes a reflection at a denser medium then it’s crest reflected as trough and vice versa. So, its phase changes at 180°.
![]()
Samacheer Kalvi 12th Physics Optics Numerical Problems
Question 1.
An object is placed at a certain distance from a convex lens of focal length 20 cm. Find the distance of the object if the image obtained is magnified 4 times.
Solution:
ƒ = – 20 cm
v = – 4u
According to lens formula
\(\frac { 1 }{ f }\) = \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\)
\(\frac { 1 }{ (-20) }\) = \(\frac { 1 }{ (-4u) }\) + \(\frac { 1 }{ u }\)
\(\frac { 1 }{ (-20) }\) = \(\left[-\frac{1}{4}+1\right]\)
= \(\frac { 1 }{ u }\) \(\frac { 3 }{ 4 }\)
u = \(\frac { 3 × 20 }{ 4 }\) = -15 cm.
Question 2.
A compound microscope has a magnification of 30. The focal length of eye piece is 5 cm. Assuming the final image to be at least distance of distinct vision, find the magnification produced by the objective.
Solution:
Magnification of compound microscope, M = 30
Focal length, f = 5 cm
Least distance of distinct vision, D = 25 cm
Now, M = M0 x Me
= M0 x \(\left[1+\frac{\mathrm{D}}{f_{e}}\right]\)
30 = M0 x \(\left[1+\frac{25}{5}\right]\)
M0 = \(\frac { 30 }{ 6 }\) = 5
Question 3.
An object is placed in front of a concave mirror of focal length 20 cm. The image formed is three times the size of the object. Calculate two possible distances of the object from the mirror.
Solution:
m = + 3 and m = – 3; f = – 20 cm
When, m = 3
m = \(\frac { v }{ u }\) = 3
v = – 3 u
From mirror equation,
\(\frac { 1 }{ f }\) = \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\)
\(\frac { 1 }{ -20 }\) = \(\frac { 1 }{ -3u }\) + \(\frac { 1 }{ u }\)
\(\frac { 1 }{ u }\) \(\left[-\frac{1}{3}+1\right]\)
\(\frac { 1 }{ -20 }\) = \(\frac { 2 }{ 3u }\)
u = –\(\frac { 40 }{ 3 }\) cm
When, m = – 3 ⇒ v = 3u
\(\frac { 1 }{ f }\) = \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\)
\(\frac { 1 }{ -20 }\) = \(\frac { 1 }{ 3u }\) + \(\frac { 1 }{ u }\)
\(\frac { 1 }{ -20 }\) = \(\frac { 4 }{ 3u }\)
u = \(\frac { 4×20 }{ 3 }\)
u = –\(\frac { 80 }{ 3 }\) cm
Question 4.
A small bulb is placed at the bottom of a tank containing water to a depth of 80 cm.What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33. (Consider the bulb to be a point source.)
Solution:
Actual depth of the bulb in water
d1 = 80 cm = 0.8 m
Refractive index of water, p = 1.33
The given situation is shown in the figure.
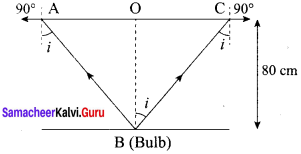
Where, i = Angle of incidence
r = Angle of refraction = 90°
Since the bulb is a point source, the emergent light can be considered as a circle AT
R= \(\frac { AC }{ 2 }\) = AO = OB
Using snell’s law, the relation for the refractive index of water is sin
µ = \(\frac { sin r }{ sin i }\)
i = sin-1 (0.75) = 48.75°
Using the given figure, we have the relation
tan i = \(\frac { OC }{ BC }\) = \(\frac { R }{ { d }_{ 1 } } \)
R = tan i x d1 = tan 48.75° x 0.8
R = 0.91 m
Area of the surface of water = πR²
= 3.14 x (0.91)² = 2.61 m²
Hence, the area of the surface of water through which the light from the bulb can emerge is approximately 2.61 m².
![]()
Question 5.
A thin converging glass lens made of glass with refractive index 1.5 has a power of + 5.0 D. When this lens is immersed in a liquid of refractive index n, it acts as a divergent lens of focal length 100 cm. What must be the value of n?
Solution:
According to Lens maker’s formula, the focal length for a convex lens placed in air can be obtained as

\(\frac { 0.5 }{ 5 }\) = \(\frac { 1.5 }{ n }\) -1
0.9 = \(\frac { 1.5 }{ n }\)
n = \(\frac { 1.5 }{ 0.9 }\) = \(\frac { 5 }{ 3 }\) -1
Question 6.
If the distance D between an object and screen is greater than 4 times the focal length of a convex lens, then there are two positions of the lens for which images are formed on the screen. This method is called conjugate foci method. If d is the distance between the two positions of the lens, obtain the equation for focal length of the convex lens.
Solution:
Let us fix the position of object and place the screen to get the enlarged image first. Also, let us fix the position of screen where we get the enlarged image.
Let D be the distance between object and screen. Let us mark the position of lens dv Then let us move the lens away from the object to get a diminished image. Let this position of lens be d2. Let d be the distance between the lens position d1 and d2. Let V be the distance b/w image and lens. Let ‘u’ be the distance between object and lens.
From mirror equation,
\(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
Let us replace v by substituting v = D – u
\(\frac { 1 }{ D-u }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
we get the equation, u² -Du + fD = 0
the quadratic equation for above equation,
u = \(\frac{\mathrm{D} \pm \sqrt{\mathrm{D}^{2}-4 f \mathrm{D}}}{2}\)
When D = 4f, we get only position of lens to get image.
This corresponds to placing the object at 2f and getting the image at 2f on the otherside. Hence, for displacement method we need D > 4 f. When this condition is satisfied we get
u1 = \(\frac{\mathrm{D}-\sqrt{\mathrm{D}^{2}-4 f \mathrm{D}}}{2}\) ; corresponding v1 – D – u2 = \(\frac{\mathrm{D}+\sqrt{\mathrm{D}^{2}-4 f \mathrm{D}}}{2}\) after changing the location
u1 =\(\frac{\mathrm{D}+\sqrt{\mathrm{D}^{2}-4f \mathrm{D}}}{2}\) ; corresponding v2 – D – u2 = \(\frac{\mathrm{D}-\sqrt{\mathrm{D}^{2}-4 f \mathrm{D}}}{2}\)
now the displacement d = v1 – u1 = u1 – v1 = \(\sqrt{D^{2}-4 f D}\)
Hence we get focal length, ƒ = \(\frac{D^{2}-d^{2}}{4 D}\)
Question 7.
A beam of light of wavelength 600 nm from a distant source falls on a single slit 1 mm wide and the resulting diffraction pattern is observed on a screen 2 m away. What is the distance between the first dark fringe on either side of the central bright fringe?
Solution:
For first minimum (n = 1) on either side of central maximum.
sin θ = \(\frac { λ }{ a }\)
Where a is width of the slit Since 0 is very small, (sin θ ≈ θ)
θ = \(\frac { λ }{ a }\) …… (1)
sin θ ≈ θ = \(\frac { x }{ 2D }\) …… (2)
Where, x is distance of first dark fringe from central maximum.
D is distance between slit and screen.
From equation (1) and (2)
\(\frac { x }{ 2D }\) = \(\frac { λ }{ a }\)
x = \(\frac { 2Dλ }{ a }\) = \(\frac { 2\times 2\times 600\times { 10 }^{ -9 } }{ 1\times { 10 }^{ -3 } } \)
= 2400 x 10-6 = 2.4 x 10-3m
x = 2.4 mm
Question 8.
In Young’s double slit experiment, the slits are 2 mm apart and are illuminated with a mixture of two wavelength λ0 = 750 nm and λ = 900 nm. What is the minimum distance from the common central bright fringe on a screen 2 m from the slits where a bright fringe from one interference pattern coincides with a bright fringe from the other?
Solution:
Now from the question we can infer that
D = 2; d = 2
n1 λ1 = n2 λ2
\(\frac{n_{1}}{n_{2}}=\frac{\lambda_{2}}{\lambda_{1}}\) =\(\frac { 900 }{ 750 }\) \(\frac { 1 }{ 2 }\)
Thus, we have
\(\frac{n_{1}}{n_{1}}=\frac{\lambda_{2}}{\lambda_{1}}\) =\(\frac { 6 }{ 5 }\)
5th and 6th fringes will coincide respectively. The minimum distance is given as
Xmin = \(\frac{n_{2} \lambda_{2} \mathrm{D}}{d}\) = \(\frac{5 \times 900 \times 10^{-9} \times 2}{2 \times 10^{-3}}\)
= 4500 x 10-6 = 4.5 x 10-3m
Xmin = 4.5 mm
![]()
Question 9.
In Young’s double slit experiment, 62 fringes are seen in visible region for sodium light of wavelength 5893 Å. If violet light of wavelength 4359 Å is used in place of sodium light, then what is the number of fringes seen?
Solution:
From young’s double slit experiment,
λ1 = 5893 Å ; λ2 = 4359 Å
\(\frac{n_{1} \lambda_{1} D}{d}\) = \(\frac{n_{2} \lambda_{2} \mathrm{D}}{d}\)
The above condition is total extent of fringes is constant for both wavelengths.
\(\frac{62 \times 5893 \times 10^{-10} \times D}{d}\) = \(\frac{n_{2} \times 4359 \times 10^{-10} \times D}{d}\)
n2 = \(\frac{62 \times 5893}{4359}\) = \(\frac{365366}{4359}\) = 83.8
n2 = 84
Question 10.
A compound microscope has a magnifying power of 100 when the image is formed at infinity. The objective has a focal length of 0.5 cm and the tube length is 6.5 cm. What is the focal length of the eyepiece.
Solution:
Magnifying Power, m = 100
Focal length of the objective,f0 = 0.5 cm
Tube length, l = 6.5 cm
Since the image is formed at infinity, the real image produced by the objective lens should lie on the focus of the eyepiece.
v0 +ƒe= 6.5 cm ….. (1)
The magnifying power for normal adjustment is given by
m = \(\left(\frac{v_{o}}{u_{o}}\right) \times \frac{\mathrm{D}}{f_{e}}\)
= – \(\left[1-\frac{v_{o}}{f_{\mathrm{o}}}\right] \frac{\mathrm{D}}{f_{e}}\)
100 = – \(\left[1-\frac{v_{o}}{0.5}\right] \times \frac{25}{f_{e}}\)
2v0 -4ƒe= 1
On solving equations (1) and (2), we get
v0 = 4.5 cm and ƒe = 2 cm
Thus, the focal length of the eyepiece is 2 cm.
Samacheer Kalvi 12th Physics Optics Additional Questions
Samacheer Kalvi 12th Physics Optics Multiple Choice Questions
Question 1.
When a ray of light enters a glass slab from air
(b) its wavelength increases
(c) its frequency increases
(d) neither its wavelength nor its frequency changes
Answer:
(a) its wavelength decreases
Hint:
Wavelength, λ = \(\frac { Velocity }{ Frequency }\) = \(\frac { u }{ v }\)
When light travels from air to glass, frequency v remains unchanged, velocity u decreases and hence wavelength X also decreases.
Question 2.
A source emits sound of frequency 600 Hz inside water. The frequency heard in air (velocity of sound in water = 1500 m/s, velocity of sound in air = 300 m/s) will be
(a) 300 Hz
(b) 120 Hz
(c) 600 Hz
(d) 6000 Hz
Answer:
(c) 600 Hz
Hint:
Frequency does not change when sound travels from one medium to another
∴ Frequency of sound in air = Frequency of sound in water = 600 Hz
Question 3.
Two beams of red and violet colours are made to pass separately through a prism (angle of the prism is 60°). In the position of minimum deviation, the angle of refraction will be
(a) 30° for both the colours
(b) greater for the violet colour
(c) greater for the violet colour
(d) equal but not 30° for both the colours
Answer:
(a) 30° for both the colours
Hint:
For any prism, r1 = r2 = A
In the position of minimum deviation for any wavelength,
r1 = r2 = \(\frac { A }{ 2 }\) = \(\frac { 60° }{ θ }\) = 30°
Question 4.
To get three images of a single object, one should have two plane mirrors at an angle of
(a) 60°
(b) 90°
(c) 120°
(d) 30°
Answer:
(b) 90°
Hint:
The number of images formed,
n = \(\frac { 360° }{ θ }\) – 1 or 3 = \(\frac { 360° }{ θ }\) -1 or θ = 90°
Question 5.
Which of the following is used in optical fibres?
(a) Total internal reflection
(b) Diffraction
(c) Refraction
(d) Scattering
Answer:
(a) Total internal reflection
Hint:
The working of optical fibres is based on total internal reflection.
![]()
Question 6.
Two lenses of power – 15 D and +15D are in contact with each other. The focal length of the combination is
(a) + 10 cm
(b) -20 cm
(c) – 10 cm
(d) + 20cm
Answer:
(c) – 10 cm
Hint P = P1 + P2 = -15 + 5= -10 D
F = \(\frac { 1 }{ P }\) = \(\frac { 1 }{ -10 }\) m = -10 cm
Question 7.
The refractive index of glass is 1.520 for red light and 1.525 for blue light. Let δ1 and δ2 be angles of minimum deviation for red and blue light respectively in a prism of this glass, then
(a) δ1, can be less than or greater than δ2 depending upon the values of δ1 and δ2
(b) δ1 > δ2
(c) δ1 < δ2
(d) δ1 = δ2
Answer:
(c) δ1 < δ2
Hint:
δ1 = (μR – 1)A, δ2 = (μB – 1)A
As, μR < μB ∴ δ1 < δ2
Question 8.
Time image formed by an objective of a compound microscope is
(a) virtual and diminished
(b) real and diminished
(c) real and enlarged
(d) virtual and enlarged
Answer:
(c) real and enlarged
Hint
The image formed by the objective of a compound microscope is real and enlarged.
Question 9.
An astronomical telescope has a large aperture to,
(a) reduce spherical aberration
(b) have high resolution
(c) increase span of observation
(d) have low dispersion
Answer:
(b) have high resolution
Question 10.
Two plane mirrors are inclined to each other at an angle of 60°. A point object is placed in between them. The total number of images produced by both the mirror is
(a) 2
(b) 4
(c) 5
( d) 6
Answer:
(c) 5
Hint:
Number of images formed, θ = \(\frac { 360° }{ θ }\) – 1 = \(\frac { 360 }{ 60 }\) = 1 = 5.
![]()
Question 11.
A boy 1.5 m tall with his eye level at 1.38 m stands before a mirror fixed on a wall. The minimum length of mirror required to view the complete image of boy is
(a) 0.75 m
(b) 0.06 m
(c) 0.69 m
(d) 0.12 m
Answer:
(a) 0.75 m
Hint
Minimum length of mirror required \(\frac { 1 }{ 2 }\) x Height of boy = \(\frac { 1 }{ 2 }\) x 1.5 = 0.75 m.
Question 12.
A pencil of light rays falls on a plane mirror and forms a real image, so the incident rays are
(a) parallel
(b) diverging
(c) converging
(d) statement is false
Answer:
(c) converging
Hint:
When converging rays fall on a plane mirror, they get reflected to a point d in front of the mirror forming a real image.
Question 13.
For a real object, which of the following can produce a real image?
(a) plane mirror
(b) concave lens
(c) convex lens
(d) concave mirror
Answer:
(d) concave mirror
Hint:
Only concave mirror produces real image provided the object is not placed between its focus and pole.
Question 14.
Which mirror is to be used to obtain a parallel beam of light from a small lamp?
(a) Plane mirror
(b) Convex mirror
(c) Concave mirror
(d) None of the above
Answer:
(c) Concave mirror
Hint:
When the small lamp is placed at the focus of the concave mirror, the reflected light is a parallel beam.
Question 15.
When a plane electromagnetic wave enters a glass slab, then which of the following will not change?
(a) Wavelength
(b) Frequency
(c) Speed
(d) Amplitude
Answer:
(b) Frequency
Only the frequency of the electromagnetic wave remains unchanged.
![]()
Question 16.
If wavelength of light in air is 2400 x 10-10 m, then what will be the wavelength of light in glass (μ = 1.5)?
(a) 1600 Å
(b) 7200 Å
(c) 1080 Å
(d) None of these
Answer:
(a) 1600 Å
Hint:
μ = \(\frac { { \lambda }_{ a } }{ { \lambda }_{ g } } \) ⇒λλg = \(\frac { { \lambda }_{ a } }{ μ } \) = \(\frac{2400 \times 10^{-10} \mathrm{m}}{1.5}\) = 1600 Å
Question 17.
Why is refractive index in a transparent medium greater than one?
(a) Because the speed of light in vacuum is always less than speed in a transparent medium.
(b) Because the speed of light in vacuum is always greater than the speed in a transparent medium.
(c) Frequency of wave changes when it Gasses medium.
(d) None of the above.
Answer:
(b) Because the speed of light in vacuum is always greater than the speed in a transparent medium.
Hint:

As c > v, μ > 1
Question 18.
The wavelength of sodium light in air is 5890 Å. The velocity of light in air is 3 x 108 ms-1. The wavelength of light in a glass of refractive index 1.6 would be close to
(a) 5890 Å
(b) 3681 Å
(c) 9424 Å
(d) 15078 Å
Answer:
(b) 3681 Å
Hint:
μ = \(\frac { { \lambda }_{ a } }{ { \lambda }_{ g } } \) ⇒λg= \(\frac { { \lambda }_{ a } }{ μ } \) = \(\frac { 5890 Å }{ 1.6 }\) = 3681 Å
Question 19.
A glass slab (μ = 1.5) of thickness 6 cm is placed over a paper. Qhat is the shift in the letters?
(a) 4 cm
(b) 2 cm
(c) 1 cm
(d) None of these
Answer:
(b) 2 cm
Hint:
Normal shift, x = \(t\left(1-\frac{1}{\mu}\right)=6\left(1-\frac{1}{1.5}\right)\) cm = 2cm
Question 20.
Light traveling from a transparent medium to air undergoes total internal reflection at an angle of incident of 45°. Then refractive index of the medium may be
(a) 1.5
(b) 1.3
(c) 1.1
(d) \(\frac { 1 }{ √2 }\)
Answer:
(a) 1.5
Hint:
μ = \(\frac{1}{\sin i_{c}}\) = \(\frac{1}{\sin 45^{\circ}}\) = √2 = 1.414 ≈ 1.5.
![]()
Question 21.
A point source of light is placed 4 m below the surface of water of refractive index 5/3. The minimum diameter of a disc which should be placed over the source, on the surface of water to cut-off all light coming out of water is
(a) infinite
(b) 6 cm
(c) 4 cm
(d) 3 cm
Answer:
(b) 6 cm
Hint:
r = \(\frac{h}{\sqrt{\mu^{2}-1}}\) = \(\frac{4}{\sqrt{\left(\frac{5}{3}\right)^{2}-1}}\) = 3 cm
Question 22.
In optical fibres, propagation of light is due to
(a) diffraction
(b) total internal reflection
(c) reflection
(d) refraction
Answer:
(b) total internal reflection
Hint:
In optical fiberes, light propagates due to tatal internal reflection.
Question 23.
Sparkling of diamond is due to
(a) reflection
(b) dispersion
(c) total internal reflection
(d) high refractive index of diamond
Answer:
(c) total internal reflection
Question 24.
For a given lens, the magnification was found to be twice as large as when the object was 0.15m distant from it as when the distance was 0.2 m. The focal length of the lens is
(a) 1.5 m
(b) 0.20 m
(c) 0.10 m
(d) 0.05 m
Asnwer:
(c) 0.10 m
Hint:
Here m1 = 2m2
\(\frac { f }{ f-0.15 }\) = 2 \(\frac { f }{ f-0.20 }\)
2f – 0.30 = f- 0.20 ; f = 0.10 m
Question 25.
Two lenses of focal lengths f1 and f2 are kept in contact coaxially. The resultant power of combination will be
(a) \(\frac { { f }_{ 1 }{ f }_{ 2 } }{ { { f }_{ 1 }-f }_{ 2 } } \)
(b) \(\frac { { f }_{ 1 }{ +f }_{ 2 } }{ { { f }_{ 1 }f }_{ 2 } } \)
(c) \({ f }_{ 1 }{ +f }_{ 2 }\)
(d) \(\frac { { f }_{ 1 } }{ { f }_{ 2 } } +\frac { { f }_{ 2 } }{ { f }_{ 1 } } \)
Answer:
(b) \(\frac { { f }_{ 1 }{ +f }_{ 2 } }{ { { f }_{ 1 }f }_{ 2 } } \)
Hint:
P = \(\frac { 1 }{ { f }_{ 1 } } +\frac { 1 }{ { f }_{ 2 } } \) = \(\frac { { f }_{ 1 }{ +f }_{ 2 } }{ { { f }_{ 1 }f }_{ 2 } } \).
![]()
Question 26.
Two lenses of power 3D and -ID are kept in contact. What is focal length and nature of combined lens?
(a) 50 cm, convex
(b) 200 cm, convex
(c) 50 cm, concave
(d) 200 cm, concave
Answer:
(a) 50 cm, convex
Hint:
P = P1 + P2 = 3 – 1 = 2D
F= \(\frac { 1 }{ P }\) = \(\frac { 1 }{ 2 }\) m = 50 cm
Question 27.
If two thin lenses are kept coaxially together, then their power is proportional (R1,R2) being the radii of curved surfaces) to
(a) R1 + R2
(b) \(\left[\frac{\mathbf{R}_{1}+\mathbf{R}_{2}}{\mathbf{R}_{1} \mathbf{R}_{2}}\right]\)
(c) \(\left[\frac{\mathrm{R}_{1} \mathrm{R}_{2}}{\mathrm{R}_{1} \mathrm{R}_{2}}\right]\)
(d) None of these
Answer:
(b) \(\left[\frac{\mathbf{R}_{1}+\mathbf{R}_{2}}{\mathbf{R}_{1} \mathbf{R}_{2}}\right]\)
Hint:
P = \(\frac{1}{f_{1}}+\frac{1}{f_{2}}=\frac{2}{\mathrm{R}_{1}}+\frac{2}{\mathrm{R}_{2}}\) = 2\(\left[\frac{\mathbf{R}_{1}+\mathbf{R}_{2}}{\mathbf{R}_{1} \mathbf{R}_{2}}\right]\)
or p ∝ \(\left[\frac{\mathbf{R}_{1}+\mathbf{R}_{2}}{\mathbf{R}_{1} \mathbf{R}_{2}}\right]\)
Question 28.
A ray incident at 15° on one refracting surface of a prism of angle 60°, suffers a deviation of 55°. What is the angle of emergance?
(a) 95°
(b) 45°
(c) 30°
(d) none of these
Answer:
(d) none of these
Hint:
A + δ = i + each
60° + 55° = 15° + each e = 115 -15 =100°
Question 29.
Dispersion of light is caused due to
(a) Wavelength
(b) intensity of light
(c) density of medium
(d) none of these
Answer:
(a) Wavelength
Hint:
Dispersion is due to the dependence of the speed of a wave on its wavelength in any medium.
Question 30.
White light is incident on one of the refracting surfaces of a prism of angle 50°. If the refractive indices for red and blue colours are 1.641 and 1.659 respectively, the angular separation between these two colours when they emerge out of the prism is
(a) 0.9°
(b) 0.09°
(c) 1.8°
(d) 1.2°
Answer:
(b) 0.09°
Hint:
Angular dispersion,
δB – δR = (µB – µR) A
= (1.659 – 1.641) x 5° = 0.09°
Question 31.
The sky would appear red instead of blue if
(a) atmospheric particles scatter blue light more than red light
(b) atmospheric particles scatter all colours equally
(c) atmospheric particle scatter red light more than blue light
(d) the sun was much hotter
Answer:
(c) atmospheric particle scatter red light more than blue light
Question 32.
A setting sun appears to be at an altitude higher than it really is. This is because of
(a) absorption of light
(b) reflection of light
(c) refraction of light
(d) dispersion of light
Answer:
(c) refraction of light
Hint:
This is due to refraction of light by the earth’s atmosphere.
Question 33.
The reddish appearance of rising and setting sun is due to
(a) reflection of light
(b) diffraction of light
(c) scattering of light
(d) interference of light
Answer:
(c) scattering of light
Hint:
The reddish appearance of the rising and the setting sun is due to scattering of light.
Question 34.
In the formation of a rainbow, the light from the sun on water droplets undergoes
(a) dispersion only
(b) only total internal reflection
(c) dispersion and total internal reflection
(d) none of the above
Answer:
(c) dispersion and total internal reflection
Hint:
Rainow is formed due to dispersion of sunlight by raindrops which also deviate the colours by total internal reflection.
Question 35.
The angular magnification of a simple microscope can be increased by increasing
(a) focal length of lens
(b) size of object
(c) aperture of lens
(d) power of lens
Answer:
(b) size of object
![]()
Question 36.
For compound microscope f0 = 1 cm, fe = 2.5 cm. An object is placed at distance 1.2 cm from objective lens. What should be length of microscope for normal adjustment?
(a) 8.5 cm
(b) 8.3 cm
(c) 6.5 cm
(d) 6.3 cm
Answer:
(a) 8.5 cm
Hint:
In the normal adjustment of a compound microscope, L = υ0 + υe = \(\frac{υ_{0} f_{e}}{υ_{0}+f_{e}}\) + fe = \(\frac { 1.2×1 }{ -1.2+1 }\) + 2.5 = 6 + 25 = 8.5 cm
Question 37.
Magnifying power of an astronomical telescope for normal vision with usual notation is
(a) -f0 / fe
(b) -f0 x fe
(c) -f0 / f0
(d) -f0 + fe
Answer:
(a) -f0 / fe
Hint:
In normal adjustment of the telescope, m = -f0 / fe
Question 38.
F1 and F2 are focal length of objective and eyepiece respectively of the telescope. The angular magnification for the given telescope is equal to
(a) \(\frac {F_{1}}{F_{2}}\)
(b) \(\frac { { F }_{ 2 } }{ { F }_{ 1 } } \)
(c) \(\frac { { F }_{ 1 }{ F }_{ 2 } }{ { F }_{ 1 }+{ F }_{ 2 } } \)
(d) \(\frac { { F }_{ 1 }+{ F }_{ 2 } }{ { F }_{ 1 }{ F }_{ 2 } } \)
Answer:
(a) \(\frac { { F }_{ 1 } }{ { F }_{ 2 } } \)
Hint:
In normal adjustment of the telescope, \(\left| m \right| \) = \(\frac { { f }_{ 0 } }{ { f }_{ e } } \) = \(\frac { { F }_{ 1 } }{ { F }_{ 2 } } \)
Question 39.
Focal length of objective and eyepiece of telescope are 200 cm and 4 cm respectively. What is length of telescope for normal adjustment?
(a) 196 cm
(b) 204 cm
(c) 250 cm
(d) 225 cm
Answer:
(b) 204 cm
Hint L = \(-{ f }_{ 0 }+{ f }_{ e }\) = 200 + 4 = 204 cm
Question 40.
For normal vision, what is minimum distance of object from eye?
(a) 30 cm
(b) 25 cm
(c) Infinite
(d) 40 cm
Answer:
(b) 25 cm
Hint:
For normal eye, the least distance of distinct vision is 25 cm.
![]()
Question 41.
The focal length of the objective and eyepiece of a telescope are respectively 100 cm and 2 cm. The moon subtends angle of 0.5° ; the angle subtended by the moon’s image will be
(a) 10°
(b) 250
(e) 100°
(d) 75°
Answer:
b) 250
Hint ;
m = \(\frac { β }{ α }\) β = \(\frac { { f }_{ 0 } }{ { f }_{ e } } \) ; α = \(\frac { 100 }{ 2 }\) x 0.5° = 25°
Question 42.
A person cannot clearly see distance more than 40 cm. He is advised to use lens of power,
(a) – 2.5 D
(b) 2.5 D
(c) – 6.25 D
(d) 1.5 D
Answer:
(a) – 2.5 D
Hint;
For the remedial lens, u = ∞,
v = – 40 cm = – 0.40 m
∴ \(\frac { 1 }{ f }\) = \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ -0.40 }\) – \(\frac { 1 }{ ∞ }\) = -2.5 ⇒ P = 2.5D
Question 43.
The light gathering power of a camera lens depends on
(a) its diameter only
(b) ratio of diameter and focal length
(c) product of focal length and diameter
(d) wavelength of the light used
Answer:
(a) its diameter only
Hint:
The light gathering power of a camera lens is proportional to its area or to the square of its diameter.
Question 44.
Amount of light entering into the camera depends upon
(a) focal length of objective lens
(b) product of focal length and diameter of the objective lens
(c) distance of object from camera
(d) aperture setting of the camera
Answer:
(d) aperture setting of the camera
Hint:
The amount of light entering into the camera depends upon the aperture setting of the camera.
Question 45.
Line spectrum can be obtained from
(a) sun
(b) candle
(c) mercury vapour lamp
(d) electric bulb
Answer:
(c) mercury vapour lamp
![]()
Question 46.
The Production of band spectra is caused by
(a) atomic nuclei
(b) hot metals
(c) molecules
(d) electrons
Answer:
(c) molecules
Question 47.
Two mirrors are kept at 60° to each other and a body is placed at middle. The total number of images formed is
(a) six
(b) four
(c) five
(d) three
Answer:
(a) six
Hint:
Number of images formed, n = \(\frac { 360 }{ θ }\) -1 = \(\frac { 360 }{ 60 }\) -1 = 5
Question 48.
A point source kept at a distance of 1000 m has a illumination I. To change the illumination to 161, the new distance should become
(a) 250 m
(b) 500 m
(c) 750 m
(d) 800 m
Answer:
(a) 250 m
Hint:
\(\frac{I_{2}}{I_{1}}=\left(\frac{r_{1}}{r_{2}}\right)^{2}\)
\(\frac{16 \mathrm{I}_{1}}{\mathrm{I}_{1}}=\frac{(1000)^{2}}{r_{2}^{2}}\) ; r2 \(\frac { 1000 }{ 4 }\) = 250 cm
Question 49.
A concave mirror of focal length 15 cm forms an image having twice the linear dimensions of the object. The position of the object, when the image is virtual will be
(a) 22.5 cm
(b) 7.5 cm
(c) 30 cm
(d) 45 cm
Answer:
(b) 7.5 cm
Hint:
For virtual images, m = \(\frac { -v }{ u }\) = + 2 or v = – 2u
As \(\frac { 1 }{ u }\) + \(\frac { 1 }{ v }\) = \(\frac { 1 }{ f }\)
∴ \(\frac { 1 }{ u }\) – \(\frac { 1 }{ 2u }\) = \(\frac { 1 }{ -15 }\) or \(\frac { 1 }{ 2u }\) = \(\frac { 1 }{ -15 }\) ⇒ u = -7.5 cm
Question 50.
when a ray of light enters a glass slab, then
(a) its frequency and velocity change
(b) only frequency changes
(c) its frequency and wavelength change
(d) its frequency does not change
Answer:
(d) its frequency does not change
Hint:
When a ray of light enters a glass slab, its velocity and wavelength change while frequency does not change.
![]()
Question 51.
A light wave of frequency u and wavelength A travels from air to glass. Then,
(a) y changes
(b) y does not change, A changes
(c) A does not change
(d) y and A change
Answer:
(b) y does not change, A changes
Hint:
Same reasoning as in the above question.
Question 52.
In refraction, light waves are bent on passing from one medium to the second medium, because in the second medium.
(a) the frequency is different
(b) the coefficient of elasticity is different
(c) the speed is different
(d) the amplitude is smaller
Answer:
(c) the speed is different
Hint:
Speed of light in second medium is different than that in first medium.
Question 53.
A ray of light having wavelength 720 nm enters in a glass of refractive index 1.5. The wavelength of the ray within the glass will be
(a) 360 nm
(b) 480 nm
(e) 720 nm
(d) 1080 nm
Answer:
(b) 480 nm
Hint:
\({ \lambda }_{ g }\) = \(\frac { { \lambda }_{ 0 } }{ \mu } \) = \(\frac { 790nm }{ 1.5 }\) = 480nm
Question 54.
Brilliance of a diamond is due to
(a) shape
(b) cutting
(c) reflection
(d) total internal reflection
Answer:
(d) total internal reflection
Hint:
Brilliance of a diamond is due to total internal reflection of light.
Question 55.
An endoscope is employed by a physician to view the internal parts of a body organ. If is based on the principle of
(a) refraction
(b) reflection
(c) total internal reflection
(d) dispersion
Answer:
(c) total internal reflection
Hint:
An endoscope is made of optical fibres which work on the principle of total internal reflection.
![]()
Question 56.
‘Mirage’ is a phenomenon due to
(a) reflection of light
(b) refraction of light
(c) total internal reflection of light
(d) diffraction of light Hint Mirage occurs due to total internal reflection of light.
Answer:
(c) total internal reflection of light
Question 57.
Two lenses of power +12D and -2D are combined together. What is their equivalent focal length?
(a) 10 cm
(b) 12.5 cm
(c) 16.6 cm
(d) 8.33 cm
Answer:
(a) 10 cm
Hint:
P = P1 + P2 = + 12 – 2 = 10 D
F = \(\frac { 1 }{ P }\) = \(\frac { 1 }{ 10 }\)m = 10 cm
Question 58.
If two lenses of power + 1.5 D and + 1.0 D are placed in contact, then the effective power of combination will be
(a) 2.5 D
(b) 1.5 D
(c) 0.5 D
(d) 3.25 D
Answer:
(a) 2.5 D
Hint:
P = P1 + P2 = + 1.5 + 1.0 = + 2.5D
Question 59.
The angle of a prism is 6° and its refractive index for green light is 1.5. If a green ray passes through it, the deviation will be
(a) 30°
(b) 15°
(c) 3°
(d) 0°
Answer:
(c) 3°
Hint:
5 = (p – 1) A = (1.5 – 1) x 6 = 3°
Question 60.
Sky appears to be blue in clear atmosphere due to light’s
(a) diffraction
(b) dispersion
(c) scattering
(d) polarisation
Answer:
(c) scattering
Hint:
Sky appears blue due to scattering of light by atmospheric modecules.
![]()
Question 61.
One can not see through fog, because
(a) fog absorbs the light
(b) light suffers total reflection at droplets
(c) refractive index of the fog is infinity
(d) light is scattered by the droplets
Answer:
(d) light is scattered by the droplets
Question 62.
Fraunhofer lines of the solar system is an example of
(a) emission lines spectrum
(b) emission band spectrum
(c) continuous emission spectrum
(d) line absorption spectrum
Answer:
(d) line absorption spectrum
Hint:
Fraunhofer lines is an example of line absorption spectrum.
Question 63.
A person using a lens as a sample microscope sees an
(a) inverted virtual image
(b) inverted real magnified image
(c) upright virtual image
(d) upright real magnified image
Answer:
(d) upright real magnified image
Hint:
A person sees an upright virtual image in a simple microscope.
Question 64.
Four lenses of focal length + 10 cm, + 50 cm, + 100 cm and + 200 cm are available for making an astronomical telescope. To produce the largest magnification, the focal length of the eyepiece should be
(a) + 10 cm
(b) + 50 cm
(c) + 100 cm
(d) + 200 cm
Answer:
(a) + 10 cm
Hint:
To produce the largest magnification, the eyepiece should have minimum focal length.
Question 65.
The camera lens has an aperture of f and the exposure time is 1/60 s. What will be the new exposure time if the aperture become 1.4f?
(a) \(\frac { 1 }{ 42 }\) s
(b) \(\frac { 1 }{ 56 }\) s
(c) \(\frac { 1 }{ 72 }\) s
(d) \(\frac { 1 }{ 31 }\) s
Answer:
(d) \(\frac { 1 }{ 31 }\) s
Hint:
Time of exposure ∝ (f – number)2
\(\frac{t}{\left(\frac{1}{60}\right)}=\left(\frac{1.4}{1}\right)^{2}\) ⇒ t = \(\frac { 1.4×1.4 }{ 60 }\) ≈ \(\frac { 1 }{ 31 }\) s.
![]()
Question 66.
For a person near point of vision is 100 cm. Then the power of lens he must wear so as have normal vision, should be
(a) + ID
(b) – ID
(c) + 3D
(d) – 3D
Answer:
(c) + 3D
Hint:
f = \(\frac { yD }{ y-D }\) = \(\frac { 100×25 }{ 100-25 }\) = \(\frac { 100 }{ 3 }\) cm = \(\frac { 1 }{ 3 }\) cm ; P = \(\frac { 1 }{ f }\) = +3d
Question 67.
Ray optics is valid, when characteristic dimension ions are
(a) much smaller than the wavelength of light
(b) much larger than the wavelength of light
(c) of the same order as the wavelength of light
(d) of the order of one millimetre
Hint:
Ray optics is valid, when characteristic dimensions are much larger than the wavelength of
light.
Question 68.
A tall man of height 6 feet, want to see his full image. Then required minimum length of the mirrorwillbe
(a) 12 feet
(b) 3 feet
(e) 6 feet
(d) any length
Hint:
inimum height of mirror required for seeing full image Height of the man = 3 feet.
Question 69.
The refractive index of water is 1.33. What will be the speed of light in water?
(a) 3 x 108 ms-1
(b) 2.26 x 108 ms-1
(c) 4 x 108 ms-1
(d) 1.33 x 108 ms-1
Answer:
(b) 2.26 x 108 ms-1
Hint:
As, μ = \(\frac { c }{ v }\) ⇒ v = \(\frac { c }{ μ }\) = \(\frac { 3\times { 10 }^{ 8 } }{ 1.33 } \) = 2.26 x 108 ms-1
Question 70.
A beam of monochromatic light is refracted from vacuum into a medium of refractive index
1.5. The wavelength of refracted light will be
(a) same
(b) dependent on intensity of refracted light
(c) larger
(d) smaller
Answer:
(d) smaller
Hint:
As light enters the medium, its wavelength decreases and becomes equal to \(\frac { λ }{ μ }\).
![]()
Question 71.
Optical fibers are based on
(a) total internal reflection
(b) less scattering
(c) refraGtion
(d) less absorption coefficient
Answer:
(a) total internal reflection
Question 72.
A convex lens is dipped in a liquid, whose refractive index is equal to the refractive index of the lens. Then, its focal length will
(a) become zero
(b) becomes infinite
(e) remain unchanged
(d) become small, but non-zero
Answer:
(b) becomes infinite
Hint:
\(\frac { 1 }{ { f }_{ 1 } } \) = \(\left(\frac{\mu_{g}}{\mu_{e}}-1\right)\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\) = (1 – 1) \(\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\) = 0 ; f1 = ∞
Question 73.
A convex lens and a concave lens, each having same focal length of 25 cm, are put in contact to form a combination of lenses. The power of the combination (in diopter) is
(a) zero
(b) 25
(c) 50
(d) infinite
Answer:
(a) zero
Hint:
\(\frac { 1 }{ F }\) = \(\frac { 1 }{ { f }_{ 1 } } \) + \(\frac { 1 }{ { f }_{ 2 } } \) = \(\frac { 1 }{ +25 }\) + \(\frac { 1 }{ -25 }\) = 0 ; P = \(\frac { 1 }{ F }\) = 0
Question 74.
The focal length of a converging lens is measured for violet, green and red colours. If is fV, fG and fR respectively. We will get
(a) fV = fG
(b) fG = fR
(c) fV < fR
(d) fV > fR
Answer:
(c) fV < fR
Hint:
\(\frac { 1 }{ f }\) = (μ – 1) \(\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\) i.e., f ∝ \(\frac { 1 }{ μ – 1 }\)
As μV > μR, so, fV < fR
Question 75.
Rainbow is formed due to combination of
(a) refraction and scattering
(b) refraction and absorption
(c) dispersion and total internal reflection
(d dispersion and focusing
Answer:
(c) dispersion and total internal reflection
Hint:
Rainbow is formed due to dispersion and total internal reflection of sunlight by raindrops.
![]()
Question 76.
The blue colour of the sky is due to the phenomenon of
(a) scattering
(b) dispersion
(c) reflection
(d) refraction
Answer:
(a) scattering
Hint:
The blue colour of the sky is due to the scattering of sunlight by atmospheric molecules.
Question 77.
An astronomical telescope often fold angular magnification has a length of 44 cm. The focal length of the object is
(a) 4 cm
(b) 40 cm
(c) 44 cm
(d) 440 cm
Answer:
(b) 40 cm
Hint:
Here, f0 + fe = 44 cm
m =\(\frac { { f }_{ 0 } }{ { f }_{ e } } \) (or) f0 = 10 fe
∴ 10 fe + 10 fe = 44 cm (or) fe = 4 cm
Hence, f0 = 10 x 4 (or) f0 = 40 cm
Question 78.
Exposure time of a camera lens at the \(\frac { f }{ 2.8 }\) Setting is \(\frac { 1 }{ 200 }\) second. The correct time of exposure at \(\frac { f }{ 5.6 }\) is
(a) 0.20 second
(b) 0.40 second
(c) 0.02 second
(d) 0.04 second
Answer:
(c) 0.02 second
Hint:
Time of exposure, t ∝ (f- number)2
∴ \(\frac{t}{\left(\frac{1}{200}\right)}=\left(\frac{5.6}{2.8}\right)^{2}\) = 4 ⇒ t = 0.02s
Question 79.
Which of the following is not due to total internal reflection?
(a) Working of optical fibre
(b) Difference between apparent and real depth of a pond
(c) Mirage on hot summer day
(d) Brilliance of diamond
Answer:
(b) Difference between apparent and real depth of a pond
Hint:
Difference between apparent and real depth of a pond is due to refraction of light and the other three phenomena involve total internal reflection.
Question 80.
An object is placed at a distance of 0.5 m infront of a plane mirror. The distance between object and image will be
(a) 0.25 m
(b) 0.5 m
(c) 1.0 m
(d) 2.0 m
Answer:
(c) 1.0 m
Hint:
Distance between object and image = 0.5 + 0.5 = 1.0 m.
![]()
Question 81.
An observer moves towards a stationary plane mirror at a speed of 4 ms-1 with what speed – will his image move towards him?
(a) 2 ms-1
(b) 4 ms-1
(c) 8 ms-1
(d) the image will stay at rest
Answer:
(c) 8 ms-1
Hint:
Speed of the image towards the observer = 2 x 4 = 8 ms-1
Question 82.
If two mirrors are kept at 60° to each other and a body is placed at the middle, then total number of images formed is
(a) six
(b) four
(c) five
(d) three
Answer:
(c) five
Hint:
Number of images formed = \(\frac { 360 }{ θ }\) -1 = \(\frac { 360 }{ 60 }\) -1 = 5
Question 83.
If an object is placed at 10 cm infront of a concave mirror of focal length 15 cm. The magnification of image is
(a) -1.5
(b) 1.5
(c) -3
(d) 3
Answer:
d) 3
Hint:
m = \(\frac { f }{ f-u }\) = \(\frac { -15 }{ -15(-10) }\) = +3
Question 84.
An object of length 2.5 cm is placed at the principal axis of a concave mirror at a distance 1.5f. The image height is
(a) + 5 m
(b) -5 cm
(c) – 10 cm
(d) + 1 cm
Answer:
(b) -5 cm
Hint:
m = \(\frac { f }{ f-u }\) = \(\frac { f }{ f-1.5f}\) = -2cm
Height image = m x height of object -2 x 2.5 = – 5 cm
Question 85.
Which of the following mirror is used by a dentist to examine a small cavity?
(a) Concave mirror
(b) Convex mirror
(c) Combination of (a) and (b)
(d) None of these
Answer:
(a) Concave mirror
Hint:
A concave mirror, because it forms erect and enlarged image when held closer to the cavity.
![]()
Question 86.
When a ray of light enters from one medium to another, then which of the following does not change?
(a) Frequency
(b) Wavelength
(c) Speed
(d) Amplitude
Answer:
(a) Frequency
Hint:
Only frequency remains unchanged.
Question 87.
When light travels from one medium to the other medium of which the refractive index is different, then which of the following will change?
(a) Frequency, wavelength and velocity
(6) Frequency and wavelength
(c) Frequency and velocity
(d) Wavelength and velocity
Answer:
(d) Wavelength and velocity
Hint:
Wavelength and velocity will change while frequency remains unchanged.
Question 88.
The time taken by the light to cross a glass of thickness 4 mm and refractive index (μ = 3), will be
(a) 4 x 10-11 sec
(b) 16 x 10-11 sec
(c) 8 x 10-11 sec
(d) 24 x 10-10 sec
Answer:
(a) 4 x 10-11 sec
Hint:

\(\frac { d }{ c/a }\) = \(\frac { μd }{ c }\) = \(\frac { 3×4×10^{-3} }{ 3×10^{8} }\) = 4 × 10-11 s
Question 89.
The critical angle of a medium with respect to air is 45°. The refractive index of medium is
(a) 1.41
(b) 1.2
(c) 1.5
(d) 2
Answer:
(a) 1.41
Hint:
μ = \(\frac{1}{\sin i_{c}}\) = \(\frac { 1 }{ sin 45° }\) = \(\frac { 1 }{ 1/√2 }\) ≈ 1.41
Question 90.
If the critical angle for total internal reflection from a medium to vacuum is 30°, then velocity of light in the medium is
(a) 6 x 108 m/sec
(b) 2 x 108 m/sec
(c) 3 x 108 m/sec
(d) 1.5 x 108 m/sec
Answer:
(c) 3 x 108 m/sec
Hint:
μ = \(\frac{1}{\sin i_{c}}\) = \(\frac { c }{ v }\)
![]()
Question 91.
When a ray of light enter from one medium to another, its velocity is doubled. The critical angle for the ray for two internal reflection will be
(a) 30°
(b) 60°
(c) 90°
(d) Information is incomplete
Answer:
(a) 30°
Hint:
μ = \(\frac{1}{\sin i_{c}}\) = \(\frac { { v }_{ 1 } }{ { v }_{ 2 } } \) =\(\frac { { 2v }_{ 2 } }{ { v }_{ 2 } } \) = 2 ; sin ic = \(\frac { 1 }{ 2 }\) ∴ic = 30°
Question 92.
A driver at a depth 12 m inside water (μ = 4/3) see the sky in a cone of semi-vertical angle is
(a) sin-1\(\left( \frac { 4 }{ 3 } \right) \)
(b) tan-1\(\left( \frac { 4 }{ 3 } \right) \)
(c) sin-1\(\left( \frac { 3 }{ 4 } \right) \)
(d) 90°
Answer:
(c) sin-1\(\left( \frac { 3 }{ 4 } \right) \)
Hint:
Required semi vertical angle = Critical angle ic = sin-1 \(\frac { 1 }{ μ }\) = sin-1\(\left( \frac { 3 }{ 4 } \right) \)
Question 93.
The principle behind optical fibres is
(a) total internal reflection
(b) total external reflection
(c) both (a) and (b)
(d) diffraction
Answer:
(a) total internal reflection
Hint:
Optical fibres work on the principle of total internal reflection.
Question 94.
Air bubble in water behaves as
(а) some times concave, sometimes convex lens
(b) concave lens
(c) convex lens
(d) always refracting surface
Answer:
(b) concave lens
Question 95.
A convex lens of 40 cm focal length is combined with a concave lens of focal length 25 cm. The power of combination is
(a) -1.5 D
(b) – 6.5 D
(c) + 6.6 D
(d) + 6.5 D
Answer:
(a) -1.5 D
Hint:
P = P1 + P2 = \(\frac { 1 }{ { f }_{ 1 } } \) + \(\frac { 1 }{ { f }_{ 2 } } \) = \(\frac { 100 }{ 40 }\) + \(\frac { 100 }{ -25 }\) = -1.5d.
![]()
Question 96.
Two thin lenses, one of focal length + 60 cm and the other of focal length – 20 cm are put in contact, the combined focal length is,
(a) 15 cm
(b) – 15 cm
(c) – 30 cm
(d) 30 cm
Answer:
(c) – 30 cm
Hint:
F = \(\frac { { f }_{ 1 }{ f }_{ 2 } }{ { f }_{ 1 }{ +f }_{ 2 } } \) = \(\frac { 60 ×(-20) }{ 60-20 }\) = 30 cm
Question 97.
How does refractive index (μ) of a material vary with respect to wavelength (λ). (A and B are constants).
(a) μ = A + \(\frac { B }{ { \lambda }^{ 2 } } \)
(b) μ = A + Bλ2
(c) μ = A + \(\frac { B }{ λ }\)
(d) μ = A + Bλ
Answer:
(a) μ = A + \(\frac { B }{ { \lambda }^{ 2 } } \)
Hint:
According to cauchy’s relation, μ = A + \(\frac { B }{ { \lambda }^{ 2 } } \)
Question 98.
a prism of a refracting angle 60° is made with a material of refractive index p. For a certain wavelength of light, the angle of minimum deviation is 30°. For this wavelength, the value of p of material is
(a) 1.820
(b) 1.414
(c) 1.503
(d) 1.231
Answer:
(b) 1.414
Hint:
μ = \(\frac{\sin \left(\frac{60^{\circ}+30^{\circ}}{2}\right)}{\sin 30^{\circ}}\) = \(\frac { sin 45° }{ sin 30° }\) = \(\frac { 1 }{ √2 }\) x \(\frac { 2 }{ 1 }\) √2 = 1.414
Question 99.
Refractive index of red and violet light are 1.52 and 1.54 respectively. If the angle of prism is 10°, the angular dispersion will be
(a) 0.02°
(b) 0.20°
(c) 3.06°
(d) 30.6°
Answer:
(b) 0.20°
Hint:
Angular dispersion = δV – δR = A(μV – μV) = 10° (1.54 – 1.52) = 0.20°
Question 100.
In a simple microscope, if the final image is located at 25 cm from the eye placed close to the lens, then magnifying power is
(a) \(\frac { 25 }{ f }\)
(b) 1 + \(\frac { 25 }{ f }\)
(c) \(\frac { f }{ 25 }\)
(d) \(\frac { f }{ 25 }\) + 1
Answer:
(b) 1 + \(\frac { 25 }{ f }\)
Hint:
When the final image is formed at the least distance of distinct vision in a simple microscope,
m = 1 + \(\frac { 25 }{ f }\)
![]()
Question 101.
Magnification at least distance of distinct vision of a simple microscope of focal length 5 cm is
(a) 2
(b) 5
(c) 4
(d) 6
Answer:
(d) 6
Hint:
m = 1 + \(\frac { 25 }{ f }\) = 1 + \(\frac { 25 }{ 5 }\) = 6
Question 102.
Magnification of a compound microscope is 30. Focal length of eyepiece is 5 cm and the image is formed at a distance of distinct vision of 25 cm. The magnification of the objective
lens is
(a) 6
(b) 5
(c) 7.5
(d) 10
Answer:
(b) 5
Hint:
me = \(\frac { v }{ u}\) = \(\frac { D }{ { u }_{ c } } \) = 1 + \(\frac { D }{ { f }_{ e } } \) = 1 + \(\frac { 25 }{ 5 }\) = 6
For the compound microscope, m = m0 x me ⇒ 30 = m0 x 6 (or) m0 = 5
Question 103.
The astronomical microscope consists of objective and eyepiece. The focal length of the objective is
(a) equal to that of the eyepiece
(b) shorter than that of the eyepiece
(c) greater than that of the eyepiece
(d) five times shorter than that of eyepiece
Answer:
(c) greater than that of the eyepiece
Hint:
For producing large magnification,f0 > fe
Question 104.
The number of lenses in terrestrial telescope is
(a) 2
(b) 4
(c) 3
(d) 6
Answer:
(c) 3
Hint:
A terrestrial telescope consists of three lenses: objective, erecting lens and eyepiece.
Question 105.
An achromatic combination of lenses is formed by joining
(a) 2 convex lens
(b) 1 convex, 1 concave lens
(c) 2 concave lenses
(d) 1 convex and 1 plane mirror
Answer:
(b) 1 convex, 1 concave lens
Hint:
An achromatic doublet should satisfy the condition \(\frac { { w }_{ 1 } }{ { f }_{ 1 } } \) + \(\frac { { w }_{ 2 } }{ { f }_{ 2 } } \) = 0.
![]()
Question 106.
The amount of light received by a camera depends upon
(a) diameter only
(b) ratio of focal length and diameter
(c) product of focal length and diameter
(d) only one of the focal length
Answer:
(b) ratio of focal length and diameter
Hint:
The amount of light received by a camera depends on the ratio of the focal length and diameter of the aperture.
Question 107.
Myopia is corrected by using a
(a) cylindrical lens
(b) bifocal lens
(c) convex lens
(d) concave lens
Answer:
(d) concave lens
Question 108.
The critical angle for total internal reflection in diamond is 24.5°. The angle refractive index of diamond is
(a) 2.41
(b) 1.41
(c) 2.59
(d) 1.59
Answer:
(a) 2.41
Hint:
μ = \(\frac { 1 }{ { sin i }_{ c } } \) = \(\frac { 1 }{ sin 24.5° }\) = 2.41
Question 109.
When a glass lens with μ = 1.47 is immersed in a trough of liquid, it looks to be disappeared. The liquid in the trough could be
(a) water
(b) kerosene
(c) glycerine
(d) alcohol
Answer:
(c) glycerine
Hint:
Glass lens will disappear, if µl = µg.
Question 110.
In optical fibres, the refractive index of the core is
(a) greater than that of the cladding
(b) equal to that of the cladding
(c) smaller than that of the cladding
(d) independent of that of the cladding
Answer:
(a) greater than that of the cladding
Hint:
In optical fibres, refractive index of core material > refractive index of the cladding.
![]()
Question 111.
For a wavelength of light ‘λ’ and scattering object of size ‘a’, all wavelength are scattered nearly equally, if
(a) a = λ
(b) a >> λ
(c) a << λ
(d) a ≥ λ
Answer: (b) a >> λ
Hint:
For a >> λ, the scattering power is not selective.
Question 112.
Two coherent monochromatic light beams of intensities I and 4I are supperposed. The maximum and minimum possible intensities in the resulting beams are
(a) 5I and I
(b) 9I and I
(c) 5I and 3I
(d) 9I and 3I
Answer:
(b) 9I and I
Hint:
Imax = \((\sqrt{\mathrm{I}_{1}}+\sqrt{\mathrm{I}_{2}})^{2}\) = \((\sqrt{41}+\sqrt{1})^{2}\) = 9I
Imax = \((\sqrt{\mathrm{I}_{1}}-\sqrt{\mathrm{I}_{2}})^{2}\) = \((\sqrt{41}-\sqrt{1})^{2}\) = I
Question 113.
screen is doubled. The fringe width is
(a) unchanged
(b) halved
(c) doubled
(d) quadrupled
Answer:
(d) quadrupled
Hint:
β = \(\frac { λD }{ d }\) ; β = \(\frac { λ ×2D }{ D/2 }\) = 4β
Question 114.
In a young’s double slit experiment, 12 fringes are observed to be formed in a certain segment of the screen, when light of wavelength 600 nm is used. If the wavelength of light is changed to 400 nm, number of fringes observed in the same segment of the screen is given by
(a) 12
(b) 18
(c) 24
(d) 30
Answer:
(b) 18
Hint:
n1λ1= n2λ2 ⇒12 x 600 = n2 x 400 or n2 = 18
Question 115.
Consider ffaunhoffer diffraction pattern obtained with a single slit illuminated at normal incident. At the angular position of the first diffraction minimum the phase difference between the wavelets from the opposite edges of the slits is
(a) \(\frac { π }{ 4 }\)
(b) \(\frac { π }{ 2 }\)
(c) 2π
(d) π
Answer:
(c) 2π
Hint:
At the angular position of first minimum wavelets from opposite edges of the slits have a path difference of X and a phase difference of 2π radian.
![]()
Question 116.
A beam of light of wavelength 600 nm from a distant source falls on a single slit 1.00 mm wide and the resulting diffraction pattern is observed on a screen 2m away. The distance between the first dark fringes on either side of the central bright fringe is
(a) 1.2 cm
(b) 1.2 mm
(c) 2.4 cm
(d) 2.4 mm
Answer:
(c) 2.4 cm
Hint:
Distance between the first dark fringes on either side = width of central maximum
= \(\frac { 2Dλ }{ d }\) = \(\frac{2 \times 2 \times 600 \times 10^{-9}}{1.00 \times 10^{-3}}\) m = 2.4 x 10-3 m = 2.4mm
Question 117.
A young’s double slit experiment uses a monochromatic source. The shape of the interference fringes formed on a screen is.
(a) hyperbola
(b) circle
(c) straight line
(d) parabola
Answer:
(a) hyperbola
Hint:
In young’s double slit experiment, the fringes obtained are hyperbolic in shape. But in a small interference pattern, the fringes appear straight.
Question 118.
The initial shape of the wavefront of the beam is
(a) planar
(b) convex
(c) concave
(d) convex near the axis and concave near the periphery
Answer:
(a) planar
Hint:
As the beam is initially parallel, the shape of wavefront is planar.
Question 119.
The angle of incident at which reflected light is totally polarised for reflection from air to glass (refractive index μ) is
(a) sin-1 (μ)
(b) sin-1 \(\left( \frac { 1 }{ μ } \right) \)
(c) tan-1 \(\left( \frac { 1 }{ μ } \right) \)
(d) tan-1 (μ)
Answer:
(d) tan-1 (μ)
According to Brewster’s law,
μ = tan ip ∴ ip = tan-1 (μ)
Question 120.
According to Huygen’s principle, light is a form of
(a) particle
(b) rays
(c) wave
(d) none of the above
Answer:
(c) wave
Hint:
According to Huygen’s principle, light travels in the form of a longitudinal wave.
![]()
Question 121.
Which one of the following phenomena is not explained by Huygen’s construction of wavefront?
(a) refraction
(b) reflection
(c) diffraction
(d) origin of spectra
Answer:
(d) origin of spectra
Hint:
Huygen’s construction of wavefront cannot explain origin of spectra which can be explained on the basis of quantum theory.
Samacheer Kalvi 12th Physics Optics Additional Problems
Question 1.
Light from a point source in air falls on a convex spherical glass surface (n = 1.5, radius of curvature = 20 cm). The distance of light source from the glass surface is 100 cm. At
What position is the image formed?
Solution:
n1 = 1; n2 = 1.5
u = 100cm ; R = + 20 cm
(R is + Ve for a convex refracting surfce)
As \(\frac { 1 }{ 2 }\) = \(\frac { 1 }{ 2 }\)
\(\frac{n_{2}}{v}-\frac{n_{1}}{u}\) = \(\frac{n_{2}-n_{1}}{R}\)
\(\frac{1.5}{v}+\frac{1}{100}\) = \(\frac{1.5-1}{20}=\frac{1}{40}\)
\(\frac { 3 }{ 2v }\) = \(\frac{1}{40}-\frac{1}{100}=\frac{5-2}{200}=\frac{3}{200}\)
\(\frac { 1 }{ v }\) = \(\frac { 1 }{ 100 }\)
v = 100 cm
Thus the image is formed at a distance of 100 cm from the glass surface in the direction of incident light.
Question 2.
Find the value of critical angle for a material of refractive index √3 .
Solution:
Here, n = √3
sin ic = \(\frac { 1 }{ n }\) = \(\frac { 1 }{ √3 }\) = \(\frac { √3 }{ 3 }\)
∴ critical angle, ic = 35.3°
Question 3.
The radius of curvature of each face of biconcave lens, made of glass of refractive index 1.5 is 30 cm. Calculate the focal length of the lens in air.
Solution:
Here n = 1.5 ; R1 = – 30 cm ; R2 = 30 cm
Using len’s maker’s formula,
\(\frac { 1 }{ f }\) = (n – 1) \(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
= (1.5-1)\(\left[\frac{1}{-30}-\frac{1}{30}\right]\) = 0.5 × \(\left(\frac{-2}{30}\right)\)
\(\frac { 1 }{ f }\) = \(\frac { 1 }{ 30 }\)
f = -30
Question 4.
The radii of curvature of the faces of a double convex lens are 10 cm and 15 cm. If focal length is 12 cm. What is the refractive index of glass?
Solution:
f = +12 cm ; R1 = 10 cm ; R2 = – 15 cm ; n = ?
As, \(\frac { 1 }{ f }\) = (n – 1) \(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
\(\frac { 1 }{ 12 }\) = (n – 1) \(\left(\frac{1}{10}+\frac{1}{15}\right)\) = (n – 1) x latex]\frac { 5 }{ 30 }[/latex]
(n – 1) = \(\frac { 6 }{ 12 }\) = 0.5
n = 0.5 +1
n = 1.5
Question 5.
A double convex lens made of glass of refractive index 1.5 has its both surfaces of equal radii of curvature of 20 cm each. An object of 5 cm height is placed at a distance of 10 cm from the lens. Find the position, nature and size of the image.
Solution:
Here n = 1.5 ; R1= +20 cm ; R2 = – 20 cm
Using lens maker’s formula,
\(\frac { 1 }{ f }\) = (n – 1) \(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
(1.5-1) = \(\left[\frac{1}{20}-\frac{1}{-20}\right]\) 0.5 x \(\left(\frac{2}{20}\right)\)
\(\frac { 1 }{ f }\) = \(\frac { 1 }{ 20 }\)
f = 20 cm
Now , u = -10 cm andf = + 20 cm
From thin lens formula, \(\frac { 1 }{ v }\) = \(\frac { 1 }{ f }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ 20 }\) – \(\frac { 1 }{ 10 }\) = \(\frac { 1 }{ 20 }\)
∴ v = -20 cm
Magnification, m = \(\frac{h_{2}}{h_{1}}\)= \(\frac { v }{ u }\)
\(\frac{h_{2}}{5cm}\) = \(\frac { -20 }{ -10 }\)
h2
Hence a virtual and erect image of height 10 cm is formed at a distance of 20 cm from the lens on the same side as the the object.
![]()
Question 6.
The image obtained with a convex lens is erect and its length is four times the length of the object. If the focal length of the lens is 20 cm, calculate the object and image distances.
Solution.
Heref= 20 cm, m = + 4 for a virtual image.
To calculate u, we have
m = \(\frac { f }{ u+f }\)
Question 7.
The radius of curvature of each surface of a convex lens of refractive index 1.5 is 40 cm. Calculate its power.
Solution:
Here, n = 105 ; R1 = + 40cm = 0.40 m
R2 = – 40cm = – 0.40 m
Power (p) = \(\frac { 1 }{ f }\) = (n – 1) \(\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
= (1.5 – 1)\(\left[\frac{1}{0.40}-\frac{1}{(-0.40)}\right]\) = 0.5 x \(\frac { 2 }{ 0.40 }\)
p = 2.5 D
Question 8.
A ray of light incident on an equilateral glass prism shows minimum deviation of 30°. Calculate the speed of light through the prism.
Solution:
Here, A = 60° ; D = 30°
Refractive index, n = \(\frac{\sin \left(\frac{A+D}{2}\right)}{\sin \left(\frac{A}{2}\right)}\) = \(\frac{\sin \left(\frac{60+30}{2}\right)}{\sin \left(\frac{60}{2}\right)}\)
n = \(\frac{\sin 45^{\circ}}{\sin 30^{\circ}}\) = \(\frac{\frac{1}{\sqrt{2}}}{\frac{1}{2}}\) = √2
n = 1.414
Velocity or light in glass, v = \(\frac { c }{ n }\) = \(\frac{3 \times 10^{8}}{1.414}\)
v = 2.12 x 108 ms-1
Question 9.
Two sources of intensity I and 41 are used in an interference experiment. Find the intensity at points where the waves from two sources superimpose with a phase
(i) Zero
(ii) \(\frac { π }{ 2 }\)
(iii) π
Solution:
The resultant intensity at a point where phase difference is Φ is
IR+I1+ I2 2\(+\sqrt{\mathrm{I}_{1} \mathrm{I}_{2}}\) cos Φ
As I1 + I and I2 = 4I, therefore,
IR = I + 4I + 2\(\sqrt{I.4I}\) cos Φ
IR = 5I + 4I cos Φ
(i) When Φ = 0 ; IR = 5I + 4I cos 0 = 9I
(ii) When Φ = \(\frac { π }{ 2 }\) ; IR = 5I + 4I cos \(\frac { π }{ 2 }\) = 5I
(iii) When Φ = π ; IR = 5I + 4I cos π = 51 – 41 = I
Φ = 0 ; IR = 9I
Φ = \(\frac { π }{ 2 }\) ; IR = 5I
Φ = π ; IR = I
Question 10.
Assume that light of wavelength 600 A is coming from a star. What is the limit of resolution of a telescope whose objective has a diameter of 100 inch?
Solution:.
The limit of resolution of a telescope, dθ = \(\frac { 1.22λ }{ D }\)
D = 100 inch = 254 cm
[∴ 1 inch = 2.54 cm]
λ = 6000 Å = 6000 x 10-10 m/s
dθ = \(\frac{1.22 \times 6000 \times 10^{-10}}{254 \times 10^{-2}}\) = 2.9 x 10-7
dθ = 2.9 x 10-7 rad.
![]()
Question 11.
Two polarising sheet have their polarising directions parallel so that the intensity of the transmitted light is maximum. Through what angle must the either sheet be turned if the intensity is to drop by one-half?
Solution:
Here, I = \(\frac{I_{o}}{2}\)
Using Malus law,,
I = Io cos2 θ
\(\frac{I_{o}}{2}\) = Io cos2 θ
cos θ ± \(\frac { 1 }{ √2 }\)
θ = ± 45°, ± 135°