Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.4

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.4

Question 1.
Construct a quadratic equation with roots 7 and -3.
Solution:
Let the given roots be α = 7 and β = -3
Sum of the roots α + β = 7 + (-3)
α + β = 7 – 3 = 4
Product of the roots αβ = (7)(-3)
αβ = -21
The required quadratic equation is
x² – (sum of two roots) x + Product of the roots = 0
x² – 4x – 21 = 0

Question 2.
A quadratic polynomial has one of its zeros 1 + \(\sqrt{5}\) and it satisfies p(1) = 2. Find the quadratic polynomial.
Solution:
Given α = 1 + \(\sqrt{5}\) So, β = 1 – \(\sqrt{5}\)

The quadratic polynomial is
p(x) = x² – (α + β)x + αβ
p(x) = k (x² – 2x – 4)
p( 1) = k(1 – 2 – 4) = -5 k
Given p (1) = 2

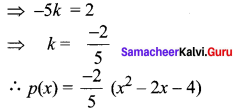
The Polynomial Roots Calculator will find the roots of any polynomial with just one click.

Question 3.
If α and β are the roots of the quadratic equation x² + \(\sqrt{2}\)x + 3 = 0, form a quadratic polynomial with zeroes 1/α, 1/β.
Solution:
α and β are the roots of the equation x² + \(\sqrt{2}\)x + 3 = 0

Question 4.
If one root of k(x – 1)² = 5x – 7 is double the other root, show that k = 2 or – 25.
Solution:
k(x – 1)² = 5x – 7
(i.e.,) k(x² – 2x + 1) – 5x + 7 = 0
x² (k) + x(-2k – 5) + k + 1 = 0
kx² – x(2k + 5) + (k + 7) = 0
Here it is given that one root is double the other.
So let the roots to α and 2α

2(4k² + 25 + 20k) = 9k (k + 7)
2(4k² + 25 + 20k) = 9k² + 63k
8k² + 50 + 40k – 9k² – 63k = 0
-k² – 23k + 50 = 0
k² + 23k – 5o = 0
(k + 25)(k – 2) = 0
k = -25 or 2

Question 5.
If the difference of the roots of the equation 2x² – (a + 1)x + a – 1 = 0 is equal to their product then prove that a = 2.
Solution:

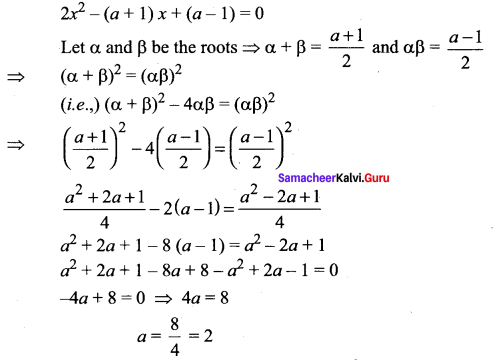
Question 6.
Find the condition that one of the roots of ax² + bx + c may be
(i) negative of the other
(ii) thrice the other
(iii) reciprocal of the other.
Solution:
(i) Let the roots be α and -β
Sum of the roots = – b/a = 0 ⇒ b = 0

(ii) Let the roots be α, 3α

Question 7.
If the equations x² – ax + b = 0 and x² – ex + f = 0 have one root in common and if the second equation has equal roots that ae = 2(b + f).
Solution:

Question 8.
Discuss the nature of roots of
(i) -x² + 3x + 1 = 0
(ii) 4x² – x – 2 = 0
(iii) 9x² + 5x = 0
Solution:
(i) -x² + 3x + 1 = 0
x² – 3x – 1 = 0 ———- (1)
Compare this equation with the equation
ax² + bx + c = 0 ——– (2)
we have a = 1, b = -3, c = -1
Discriminant = b² – 4ac
b² – 4ac = (-3)² – 4 × 1 × – 1
= 9 + 4 =13
b² – 4ac = 13 > 0
∴ The two roots are real and distinct.

(ii) 4x² – x – 2 = 0
4x² – x – 2 = 0 ——(3)
Compare this equation with the equation
ax² + bx + c = 0 (4)
we have a = 4 , b = – 1, c = – 2
Discriminant = b² – 4ac
b² – 4ac = (-1)² – 4 (4) (-2)
= 1 + 32
= 33
b² – 4ac = 33 >0
∴ The two roots are real and distinct.

(iii) 9x² + 5x = 0
9x² + 5x = 0 ——- (5)
Compare this equation with the equation
ax² + bx + c = 0 ——– (6)
we have a = 9, b = 5 , c = 0
Discriminant = b² – 4ac
b² – 4ac = 5² – 4 × 9 × 0
b² – 4ac = 25 > 0
∴ The two roots are real and distinct.

Question 9.
Without sketching the graphs find whether the graphs of the following functions will intersect the x- axis and if so in how many points.
(i) y = x² + x + 2
(ii) y = x² – 3x – 1
(iii) y = x² + 6x + 9
Solution:

Completing the Square Calculator is a free online tool that displays the variable value for the quadratic equation using completing the square method.

Question 10.
Write f(x) = x² + 5x + 4 in completed square form.
Solution:

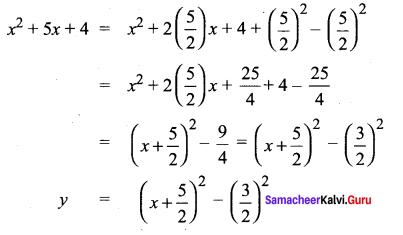
Samacheer Kalvi 11th Maths Solutions Chapter 2 Basic Algebra Ex 2.4 Additional Questions

Question 1.
Find the values of k so that the equation x² = 2x (1 + 3k) + 7(3 + 2k) = 0 has real and equal roots.
Solution:
The equation is x² – x(2) (1 + 3k) + 7 (3 + 2k) = 0
The roots are real and equal
⇒ ∆ = 0 (i.e.,) b² – 4ac = 0
Here a = 1, b = -2 (1 + 3k), c = 7(3 + 2k)
So b² – 4ac = 0
⇒ [-2 (1 + 3k)]² – 4(1) (7) (3 + 2k) = 0
(i.e.,) 4 (1 + 3k)² – 28 (3 + 2k) = 0
(÷ by 4) (1 + 3k)² – 7(3 + 2k) = 0
1 + 9k² + 6k – 21 – 14k = 0
9k² – 8k – 20 = 0
(k – 2)(9k + 10) = 0

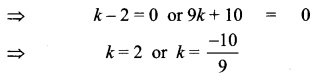
To solve the quadratic inequalities ax² + bx + c < 0 (or) ax² + bx + c > 0

Question 2.
If the sum and product of the roots of the quadratic equation ax² – 5x + c = 0 are both equal to 10 then find the values of a and c.
Solution:
The given equation is ax² – 5x + c = 0
Let the roots be α and β Given α + β = 10 and αβ = 10

Question 3.
If α and β are the roots of the equation 3x² – 4x + 1 = 0, form the equation whose roots are \(\frac{\alpha^{2}}{\beta}\) and \(\frac{\beta^{2}}{\alpha}\)
Solution:

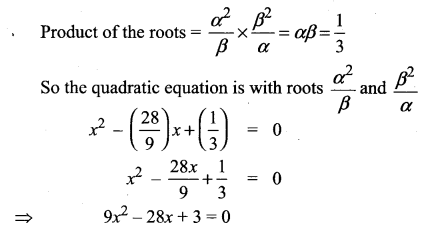
Question 4.
If one root of the equation 3x² + kx – 81 = 0 is the square of the other then find k.
Solution:

Question 5.
If one root of the equation 2x² – ax + 64 = 0 is twice that of the other then find the value of a.
Solution: